Linear Programming Question 22
Question: A shop-keeper deals in the sale of TV s and VCPs. He has 5.2 lacs to invest. He has only space for 50 pieces. ATV costs 20,000/- and a VCP costs 8,000/- From a TV and VCP he earns a profit of 1500/- and 800/- respectively. Assuming that he sells all the items that he purchases, the number of TVs and VCPs he should buy in order to Maximize his profit, is equal to
Options:
A) 60, 000
B) 55, 000
C) 51, 000
D) 47, 000
Show Answer
Answer:
Correct Answer: D
Solution:
Let x and y denote the number of TV and VCP respectively. From the given data, we have $ x\ge 0,y\ge 0,x+y\le 50. $ he has 5.2 lacs to invest.
Hence $ 20000x+8000y\le 520000. $
The profit he earns is $ 1500x+800y. $ Hence the LPP
Maximize: $ z=1500x+800y $
Subject to $ x\ge 0,y\ge 0, $
$ x+y\le 50 $ and $ 5x+2y\le 130. $
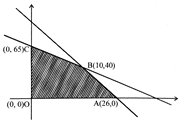
The boundary lines meet the coordinate axes at:
$ x-axis;(50,0),(26,0) $
$ y-axis; (0,50), (0,65) $
The boundary lines $ x+y=50 $ and $ 5x+2y=120 $ intersect at $ (10,40). $ the feasible region is shown as shaded.
The quadrilateral has four vertices, namely
$ 0(0,0),A(26,0),B(10,40),C(0,65). $
The maximum occurs at $ B(10,40). $
Hence he should store 10 TVs and 40 VCPs. He earns a profit of $
$ 1500\times 10+800\times 40=47,000 $