Linear Programming Question 61
Question: For the L.P. problem Min $ z=2x_1+3x_2 $ such that $ -x_1+2x_2\le 4, $ $ x_1+x_2\le 6,\ \ x_1+3x_2\ge 9 $ and $ x_1,\ x_2\ge 0 $
Options:
A) $ x_1=1.2 $
B) $ x_2=2.6 $
C) $ z=10.2 $
D) All the above
Show Answer
Answer:
Correct Answer: D
Solution:
The graph of linear programming problem is as given below
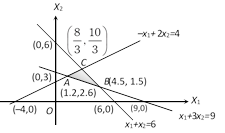
Hence the required feasible region is given by the graph whose vertices are $ A(1.2,2.6),B(4.5,1.5) $ and $ C( \frac{8}{3},\frac{10}{3} ) $
Thus objective function is minimum at $ A(1.2,2.6) $
So $ x_1=1.2,x_2=2.6 $ and $ z=2\times 1.2+3\times 2.6=10.2 $ .





