Linear Programming Question 63
Question: If $ 3x_1+5x_2\le 15 $ , $ 5x_1+2x_2\le 10 $ , $ x_1,\ x_2\ \ \ge 0 $ then the maximum value of $ 5x_1+3x_2 $ , by graphical method is
Options:
A) $ 12\frac{7}{19} $
B) $ 12\frac{1}{7} $
C) $ 12\frac{3}{5} $
D) 12
Show Answer
Answer:
Correct Answer: A
Solution:
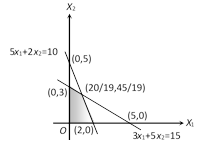
The shaded region represent the feasible region, hence $ p=5x_1+3x_2 $
Obviously it is maximum at $ ( \frac{20}{19},\frac{45}{19} ) $ Max $ p=5x_1+3x_2 $
$ =5( \frac{20}{19} )+3( \frac{45}{19} ) $
$ =\frac{100}{19}+\frac{135}{19}=\frac{235}{19}=12\frac{7}{19} $ .