Linear Programming Question 81
Question: For the L.P. problem Max $ z=3x_1+2x_2 $ such that $ 2x_1-x_2\ge 2 $ , $ x_1+2x_2\le 8 $ and $ x_1,\ x_2\ge 0 $ , $ z= $
Options:
12
24
36
40
Show Answer
Answer:
Correct Answer: B
Solution:
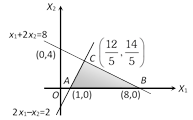
Change the inequalities into equations and draw the graph of lines, thus we get the required feasible region. It is a bounded region, bounded by the vertices $ A(1,0),B(8,0) $ and $ C( \frac{12}{5},\frac{14}{5} ) $ . Now by evaluation of the objective function for the vertices of feasible region it is found to be maximum at (8,0). Hence the solution is $ z=3\times 8+0\times 2=24 $ .