Chapter-08 Introduction to Trigonometry
There is perhaps nothing which so occupies the middle position of mathematics as trigonometry.
J.F. Herbart (1890)
8.1 Introduction
You have already studied about triangles, and in particular, right triangles, in your earlier classes. Let us take some examples from our surroundings where right triangles can be imagined to be formed. For instance :
1. Suppose the students of a school are visiting Qutub Minar. Now, if a student is looking at the top of the Minar, a right triangle can be imagined to be made, as shown in Fig 8.1. Can the student find out the height of the Minar, without actually measuring it?

Fig. 8.1
2. Suppose a girl is sitting on the balcony of her house located on the bank of a river. She is looking down at a flower pot placed on a stair of a temple situated nearby on the other bank of the river. A right triangle is imagined to be made in this situation as shown in Fig.8.2. If you know the height at which the person is sitting, can you find the width of the river?

Fig. 8.2
3. Suppose a hot air balloon is flying in the air. A girl happens to spot the balloon in the sky and runs to her mother to tell her about it. Her mother rushes out of the house to look at the balloon.Now when the girl had spotted the balloon intially it was at point A. When both the mother and daughter came out to see it, it had already travelled to another point B. Can you find the altitude of $B$ from the ground?

Fig. 8.3
In all the situations given above, the distances or heights can be found by using some mathematical techniques, which come under a branch of mathematics called ’trigonometry’. The word ’trigonometry’ is derived from the Greek words ’tri’ (meaning three), ‘gon’ (meaning sides) and ‘metron’ (meaning measure). In fact, trigonometry is the study of relationships between the sides and angles of a triangle. The earliest known work on trigonometry was recorded in Egypt and Babylon. Early astronomers used it to find out the distances of the stars and planets from the Earth. Even today, most of the technologically advanced methods used in Engineering and Physical Sciences are based on trigonometrical concepts.
In this chapter, we will study some ratios of the sides of a right triangle with respect to its acute angles, called trigonometric ratios of the angle. We will restrict our discussion to acute angles only. However, these ratios can be extended to other angles also. We will also define the trigonometric ratios for angles of measure $0^{\circ}$ and $90^{\circ}$. We will calculate trigonometric ratios for some specific angles and establish some identities involving these ratios, called trigonometric identities.
8.2 Trigonometric Ratios
In Section 8.1, you have seen some right triangles imagined to be formed in different situations.
Let us take a right triangle $ABC$ as shown in Fig. 8.4.

Fig. 8.4
Here, $\angle CAB$ (or, in brief, angle $A$ ) is an acute angle. Note the position of the side $BC$ with respect to angle $A$. It faces $\angle A$. We call it the side opposite to angle $A$. $AC$ is the hypotenuse of the right triangle and the side $AB$ is a part of $\angle A$. So, we call it the side adjacent to angle $A$.
Note that the position of sides change when you consider angle $C$ in place of $A$ (see Fig. 8.5).

Fig. 8.5
You have studied the concept of ‘ratio’ in your earlier classes. We now define certain ratios involving the sides of a right triangle, and call them trigonometric ratios.
The trigonometric ratios of the angle $A$ in right triangle $A B C$ (see Fig. 8.4) are defined as follows :
$$ \begin{aligned} \text{sine of }\angle A=\dfrac{\text{ side opposite to angle } A}{\text{ hypotenuse }}=\dfrac{BC}{AC}\\ \text{cosine of } \angle A=\dfrac{\text{ side adjacent to angle } A}{\text{ hypotenuse }}=\dfrac{AB}{AC}\end{aligned} $$
$$\text{tangent of }\angle A=\dfrac{\text{ side opposite to angle } A}{\text{ side adjacent to angle } A}=\dfrac{BC}{AB}$$
$$\text{cosecant of }\angle A=\dfrac{1}{\text{ sine of } \angle A}=\dfrac{\text{ hypotenuse }}{\text{ side opposite to angle } A}=\dfrac{AC}{BC}$$
$$\text{secant of }\angle A=\dfrac{1}{\text{ cosine of } \angle A}=\dfrac{\text{ hypotenuse }}{\text{ side adjacent to angle } A}=\dfrac{AC}{AB}$$
$$\text{ cotangent of }\angle A=\dfrac{1}{\text{ tangent of } \angle A}=\dfrac{\text{ side adjacent to angle } A}{\text{ side opposite to angle } A}=\dfrac{AB}{BC}$$
The ratios defined above are abbreviated as $\sin A, \cos A, \tan A, cosec A, \sec A$ and $\cot$ A respectively. Note that the ratios $cosec \mathbf{A}, \sec \mathbf{A}$ and $\cot \mathbf{A}$ are respectively, the reciprocals of the ratios $\sin A, \cos A$ and $\tan A$.
Also, observe that $\tan A=\dfrac{B C}{A B}=\dfrac{\dfrac{B C}{A C}}{\dfrac{A B}{A C}}=\dfrac{\sin A}{\cos A}$ and $\cot A=\dfrac{\cos A}{\sin A}$.
So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Why don’t you try to define the trigonometric ratios for angle C in the right triangle? (See Fig. 8.5)
The first use of the idea of ‘sine’ in the way we use it today was in the work Aryabhatiyam by Aryabhata, in A.D. 500. Aryabhata used the word ardha-jya for the half-chord, which was shortened to jya or jiva in due course. When the Aryabhatiyam was translated into Arabic, the word jiva was retained as it is. The word jiva was translated into sinus, which means curve, when the Arabic version was translated into Latin. Soon the word sinus, also used as sine, became common in mathematical texts throughout Europe. An English Professor of astronomy Edmund Gunter (1581-1626), first used the abbreviated notation ‘sin’.

Aryabhata C.E. $476-550$
The origin of the terms ‘cosine’ and ’tangent’ was much later. The cosine function arose from the need to compute the sine of the complementary angle. Aryabhatta called it kotijya. The name cosinus originated with Edmund Gunter. In 1674, the English Mathematician Sir Jonas Moore first used the abbreviated notation ‘cos’.
Remark : Note that the symbol sin A is used as an abbreviation for ’the sine of the angle A’. sin A is not the product of ‘sin’ and A. ‘sin’ separated from A has no meaning. Similarly, cos A is not the product of ‘cos’ and A. Similar interpretations follow for other trigonometric ratios also.
Now, if we take a point $P$ on the hypotenuse $AC$ or a point $Q$ on $AC$ extended, of the right triangle $ABC$ and draw $PM$ perpendicular to $AB$ and $QN$ perpendicular to $A B$ extended (see Fig. 8.6), how will the trigonometric ratios of $\angle A$ in $\triangle PAM$ differ from those of $\angle A$ in $\triangle CAB$ or from those of $\angle A$ in $\triangle$ QAN?

Fig. 8.6
To answer this, first look at these triangles. Is $\triangle$ PAM similar to $\triangle CAB$ ? From Chapter 6, recall the AA similarity criterion. Using the criterion, you will see that the triangles PAM and CAB are similar. Therefore, by the property of similar triangles, the corresponding sides of the triangles are proportional.
So, we have $\dfrac{AM}{AB}=\dfrac{AP}{AC}=\dfrac{MP}{BC}$
From this, we find
$ \begin{aligned} \dfrac{MP}{AP} & =\dfrac{BC}{AC}=\sin A . \end{aligned} $
Similarly, $ \begin{aligned} \dfrac{AM}{AP}=\dfrac{AB}{AC} & =\cos A, \dfrac{MP}{AM}=\dfrac{BC}{AB}=\tan A \text{ and so on. } \end{aligned} $
This shows that the trigonometric ratios of angle $A$ in $\triangle$ PAM not differ from those of angle $A$ in $\triangle CAB$.
In the same way, you should check that the value of sin A (and also of other trigonometric ratios) remains the same in $\triangle QAN$ also.
From our observations, it is now clear that the values of the trigonometric ratios of an angle do not vary with the lengths of the sides of the triangle, if the angle remains the same.
Note : For the sake of convenience, we may write $\sin ^{2} A, \cos ^{2} A$, etc., in place of $(\sin A)^{2},(\cos A)^{2}$, etc., respectively. But $cosec A=(\sin A)^{-1} \neq \sin ^{-1} A$ (it is called sine inverse A). $\sin ^{-1} A$ has a different meaning, which will be discussed in higher classes. Similar conventions hold for the other trigonometric ratios as well. Sometimes, the Greek letter $\theta$ (theta) is also used to denote an angle.
We have defined six trigonometric ratios of an acute angle. If we know any one of the ratios, can we obtain the other ratios? Let us see.
If in a right triangle $ABC, \sin A=\dfrac{1}{3}$, then this means that $\dfrac{B C}{A C}=\dfrac{1}{3}$, i.e., the lengths of the sides $BC$ and $AC$ of the triangle $A B C$ are in the ratio $1: 3$ (see Fig. 8.7). So if $BC$ is equal to $k$, then $AC$ will be $3 k$, where $k$ is any positive number. To determine other trigonometric ratios for the angle $A$, we need to find the length of the third side $A B$. Do you remember the Pythagoras theorem? Let us use it to determine the required length $AB$.

Fig. 8.7
$ AB^{2}=AC^{2}-BC^{2}=(3 k)^{2}-(k)^{2}=8 k^{2}=(2 \sqrt{2} k)^{2} $
Therefore,$\quad\quad\quad AB= \pm 2 \sqrt{2} k$
So, we get $ AB=2 \sqrt{2} k \quad(\text{ Why is } AB \text{ not }-2 \sqrt{2} k ?) $
Now, $ \quad\quad\quad \quad \cos A=\dfrac{AB}{AC}=\dfrac{2 \sqrt{2} k}{3 k}=\dfrac{2 \sqrt{2}}{3} $
Similarly, you can obtain the other trigonometric ratios of the angle A.
Remark : Since the hypotenuse is the longest side in a right triangle, the value of $\sin A$ or $\cos A$ is always less than 1 (or, in particular, equal to 1 ).
Let us consider some examples.
Example 1 : Given $\tan A=\dfrac{4}{3}$, find the other trigonometric ratios of the angle $A$.
Solution : Let us first draw a right $\triangle ABC$ (see Fig 8.8).

Fig. 8.8
Now, we know that $\tan A=\dfrac{BC}{AB}=\dfrac{4}{3}$.
Therefore, if $BC=4 k$, then $AB=3 k$, where $k$ is a positive number.
Now, by using the Pythagoras Theorem, we have
$ AC^{2}=AB^{2}+BC^{2}=(4 k)^{2}+(3 k)^{2}=25 k^{2} $
So, $AC=5 k$
Now, we can write all the trigonometric ratios using their definitions.
$ \begin{matrix} \sin A=\dfrac{BC}{AC}=\dfrac{4 k}{5 k}=\dfrac{4}{5} \\ \cos A=\dfrac{AB}{AC}=\dfrac{3 k}{5 k}=\dfrac{3}{5} \end{matrix} $
Therefore, $\cot A=\dfrac{1}{\tan A}=\dfrac{3}{4}, cosec A=\dfrac{1}{\sin A}=\dfrac{5}{4}$ and $\sec A=\dfrac{1}{\cos A}=\dfrac{5}{3}$.
Example 2 : If $\angle B$ and $\angle Q$ are acute angles such that $\sin B=\sin Q$, then prove that $\angle B=\angle Q$.
Solution : Let us consider two right triangles $ABC$ and $PQR$ where $\sin B=\sin Q$ (see Fig. 8.9).

Fig. 8.9
We have $\sin B=\dfrac{A C}{A B}$
$ \text{ and } \quad \quad \quad \quad \quad \sin Q=\dfrac{P R}{P Q} $
Then $\quad \quad \quad \dfrac{AC}{AB}=\dfrac{PR}{PQ}$
Therefore, $$ \dfrac{AC}{PR}=\dfrac{AB}{PQ}=k \text{, say } \tag{1} $$
Now, using Pythagoras theorem,
$ \begin{aligned} BC & =\sqrt{AB^{2}-AC^{2}} \end{aligned} $
and $ \begin{aligned} QR & =\sqrt{PQ^{2}-PR^{2}} \end{aligned} $
$\text{So,} \quad \dfrac{BC}{QR}=\dfrac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{PQ^{2}-PR^{2}}}=\dfrac{\sqrt{k^{2} PQ^{2}-k^{2} PR^{2}}}{\sqrt{PQ^{2}-PR^{2}}}=\dfrac{k \sqrt{PQ^{2}-PR^{2}}}{\sqrt{PQ^{2}-PR^{2}}}=k \tag{2}$
From (1) and (2), we have
$$ \dfrac{AC}{PR}=\dfrac{AB}{PQ}=\dfrac{BC}{QR} $$
Then, by using Theorem 6.4, $\Delta ACB \sim \Delta PRQ$ and therefore, $\angle B=\angle Q$.
Example 3 : Consider $\triangle ACB$, right-angled at $C$, in which $AB=29$ units, $BC=21$ units and $\angle ABC=\theta$ (see Fig. 8.10). Determine the values of

Fig. 8.10
(i) $\cos ^{2} \theta+\sin ^{2} \theta$,
(ii) $\cos ^{2} \theta-\sin ^{2} \theta$.
Solution : In $\triangle ACB$, we have
$ \begin{aligned} & A C=\sqrt{A B^{2}-B C^{2}}=\sqrt{(29)^{2}-(21)^{2}} \\ & =\sqrt{(29-21)(29+21)}=\sqrt{(8)(50)}=\sqrt{400}=20 \text{ units } \end{aligned} $
So, $\quad \sin \theta=\dfrac{A C}{A B}=\dfrac{20}{29}, \cos \theta=\dfrac{B C}{A B}=\dfrac{21}{29}$.
Now, (i) $\cos ^{2} \theta+\sin ^{2} \theta=(\dfrac{20}{29})^{2}+(\dfrac{21}{29})^{2}=\dfrac{20^{2}+21^{2}}{29^{2}}=\dfrac{400+441}{841}=1$,
and (ii) $\cos ^{2} \theta-\sin ^{2} \theta=(\dfrac{21}{29})^{2}-(\dfrac{20}{29})^{2}=\dfrac{(21+20)(21-20)}{29^{2}}=\dfrac{41}{841}$.
Example 4 : In a right triangle $A B C$, right-angled at $B$, if $\tan A=1$, then verify that
$2 \sin A \cos A=1$.
Solution : In $\triangle ABC, \tan A=\dfrac{BC}{AB}=1 \quad$ (see Fig 8.11)

Fig. 8.11
i.e., $ B C=A B $
Let $AB=BC=k$, where $k$ is a positive number.
Now, $$ \begin{aligned} AC & =\sqrt{AB^{2}+BC^{2}} \\ & =\sqrt{(k)^{2}+(k)^{2}}=k \sqrt{2} \end{aligned} $$
Therefore, $ \sin A=\dfrac{B C}{A C}=\dfrac{1}{\sqrt{2}} \text{ and } \cos A=\dfrac{A B}{A C}=\dfrac{1}{\sqrt{2}} $
So, $\quad 2 \sin A \cos A=2(\dfrac{1}{\sqrt{2}})(\dfrac{1}{\sqrt{2}})=1$, which is the required value.
Example 5 : In $\Delta OPQ$, right-angled at $P$, $OP=7 cm$ and $OQ-PQ=1 cm$ (see Fig. 8.12). Determine the values of $\sin Q$ and $\cos Q$.

Fig. 8.12
Solution : In $\triangle OPQ$, we have
$ OQ^{2}=OP^{2}+PQ^{2} $
i.e., $ (1+P Q)^{2}=OP^{2}+PQ^{2} $(why?)
i.e., $ \quad 1+PQ^{2}+2 PQ=OP^{2}+PQ^{2} $
i.e., $ \quad 1+2 P Q=7^{2} \quad \quad \quad \quad \text{(Why?)} $
i.e., $ PQ=24 ~cm \text{ and } OQ=1+PQ=25 ~cm $
So, $\quad \sin Q=\dfrac{7}{25}$ and $\cos Q=\dfrac{24}{25}$.
EXERCISE 8.1
1. In $\triangle ABC$, right-angled at $B, AB=24 cm, BC=7 cm$. Determine :
(i) $\sin A, \cos A$
(ii) $\sin C, \cos C$
Show Answer
Solution
Applying Pythagoras theorem for $\triangle A B C$, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$=(24 cm)^{2}+(7 cm)^{2}$
$=(576+49) cm^{2}$
$=625 cm^{2}$
$\therefore AC=\sqrt{625} cm=25 cm$

(i) $\sin A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Hypotenuse }}=\dfrac{BC}{AC}$
$=\dfrac{7}{25}$
$\cos A=$
$\dfrac{\text{ Side adjacent to } \angle A}{\text{ Hypotenuse }}=\dfrac{AB}{AC}=\dfrac{24}{25}$
(ii)

$ \begin{aligned} & \sin C=\dfrac{\text{ Side opposite to } \angle C}{\text{ Hypotenuse }}=\dfrac{AB}{AC} \\ & =\dfrac{24}{25} \end{aligned} $
$ \begin{aligned} & \dfrac{\text{ Side adjacent to } \angle C}{\text{ Hypotenuse }}=\dfrac{BC}{AC} \\ & \cos C= \\ & =\dfrac{7}{25} \end{aligned} $
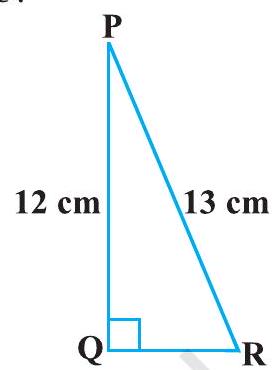
2. In Fig. 8.13, find tan $P-\cot R$.

Fig. 8.13
Show Answer
Solution
Applying Pythagoras theorem for $\triangle PQR$, we obtain
$PR^{2}=PQ^{2}+QR^{2}$
$(13 cm)^{2}=(12 cm)^{2}+QR^{2}$
$169 cm^{2}=144 cm^{2}+QR^{2}$
$25 cm^{2}=QR^{2}$
$QR=5 cm$

$ \begin{aligned} \tan P & =\dfrac{\text{ Side opposite to } \angle P}{\text{ Side adjacent to } \angle P}=\dfrac{QR}{PQ} \\ & =\dfrac{5}{12} \end{aligned} $
$ \begin{aligned} \cot R & =\dfrac{\text{ Side adjacent to } \angle R}{\text{ Side opposite to } \angle R}=\dfrac{QR}{PQ} \\ & =\dfrac{5}{12} \end{aligned} $
$\tan P-\cot R=\dfrac{5}{12}-\dfrac{5}{12}=0$
3. If $\sin A=\dfrac{3}{4}$, calculate $\cos A$ and $\tan A$.
Show Answer
Solution
Let $\triangle A B C$ be a right-angled triangle, right-angled at point $B$.

Given that,
$ \begin{aligned} & \sin A=\dfrac{3}{4} \\ & \dfrac{BC}{AC}=\dfrac{3}{4} \end{aligned} $
Let $BC$ be $3 k$. Therefore, $AC$ will be $4 k$, where $k$ is a positive integer.
Applying Pythagoras theorem in $\triangle A B C$, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$(4 k)^{2}=A B^{2}+(3 k)^{2}$
$16 k^{2}-9 k^{2}=AB^{2}$
$7 k^{2}=A B^{2}$
$AB=\sqrt{7} k$
$\cos A=\dfrac{\text{ Side adjacent to } \angle A}{\text{ Hypotenuse }}$
$=\dfrac{AB}{AC}=\dfrac{\sqrt{7 k}}{4 k}=\dfrac{\sqrt{7}}{4}$
$\tan A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Side adjacent to } \angle A}$
$=\dfrac{BC}{AB}=\dfrac{3 k}{\sqrt{7} k}=\dfrac{3}{\sqrt{7}}$
4. Given $15 \cot A=8$, find $\sin A$ and $\sec A$.
Show Answer
Solution
Consider a right-angled triangle, right-angled at $B$.

$\cot A=\dfrac{\text{ Side adjacent to } \angle A}{\text{ Side opposite to } \angle A}$
$=\dfrac{AB}{BC}$
It is given that,
$ \begin{aligned} \cot A & =\dfrac{8}{15} \\ \dfrac{AB}{BC} & =\dfrac{8}{15} \end{aligned} $
Let $A B$ be $8 k$.Therefore, $B C$ will be $15 k$, where $k$ is a positive integer.
Applying Pythagoras theorem in $\triangle A B C$, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$=(8 k)^{2}+(15 k)^{2}$
$=64 k^{2}+225 k^{2}$
$=289 k^{2}$
$AC=17 k$
$ \begin{aligned} \sin A & =\dfrac{\text{ Side opposite to } \angle A}{\text{ Hypotenuse }}=\dfrac{BC}{AC} \\ & =\dfrac{15 k}{17 k}=\dfrac{15}{17} \end{aligned} $
$\sec A=\dfrac{\text{ Hypotenuse }}{\text{ Side adjacent to } \angle A}$
$ =\dfrac{AC}{AB}=\dfrac{17}{8} $
5. Given $\sec \theta=\dfrac{13}{12}$, calculate all other trigonometric ratios.
Show Answer
Solution
Consider a right-angle triangle $\triangle A B C$, right-angled at point $B$.

$\sec \theta=\dfrac{\text{ Hypotenuse }}{\text{ Side adjacent to } \angle \theta}$
$\dfrac{13}{12}=\dfrac{AC}{AB}$
If $AC$ is $13 k, AB$ will be $12 k$, where $k$ is a positive integer.
Applying Pythagoras theorem in $\triangle ABC$, we obtain
$(A C)^{2}=(A B)^{2}+(B C)^{2}$
$(13 k)^{2}=(12 k)^{2}+(B C)^{2}$
$169 k^{2}=144 k^{2}+BC^{2}$
$25 k^{2}=BC^{2}$
$BC=5 k$
$\sin \theta=\dfrac{\text{ Side opposite to } \angle \theta}{\text{ Hypotenuse }}=\dfrac{B C}{A C}=\dfrac{5 k}{13 k}=\dfrac{5}{13}$
$\cos \theta=\dfrac{\text{ Side adjacent to } \angle \theta}{\text{ Hypotenuse }}=\dfrac{AB}{AC}=\dfrac{12 k}{13 k}=\dfrac{12}{13}$
$\tan \theta=\dfrac{\text{ Side opposite to } \angle \theta}{\text{ Side adjacent to } \angle \theta}=\dfrac{BC}{AB}=\dfrac{5 k}{12 k}=\dfrac{5}{12}$
$\cot \theta=\dfrac{\text{ Side adjacent to } \angle \theta}{\text{ Side opposite to } \angle \theta}=\dfrac{AB}{BC}=\dfrac{12 k}{5 k}=\dfrac{12}{5}$
$cosec \theta=\dfrac{\text{ Hypotenuse }}{\text{ Side opposite to } \angle \theta}=\dfrac{AC}{BC}=\dfrac{13 k}{5 k}=\dfrac{13}{5}$
6. If $\angle A$ and $\angle B$ are acute angles such that $\cos A=\cos B$, then show that $\angle A=\angle B$.
Show Answer
Solution
Let us consider a triangle $A B C$ in which $C D \perp A B$.

It is given that
$\cos A=\cos B$ $\Rightarrow \dfrac{AD}{AC}=\dfrac{BD}{BC}$
We have to prove $\angle A=\angle B$. To prove this, let us extend $A C$ to $P$ such that $B C=C P$.

From equation (1), we obtain
$\dfrac{AD}{BD}=\dfrac{AC}{BC}$
$\Rightarrow \dfrac{AD}{BD}=\dfrac{AC}{CP}$
(By construction, we have $BC=CP$ )
By using the converse of B.P.T,
$CD \mid BP$
$\Rightarrow \angle ACD=\angle CPB$ (Corresponding angles) ..
And, $\angle BCD=\angle CBP$ (Alternate interior angles)
By construction, we have $BC=CP$.
$\therefore \angle CBP=\angle CPB$ (Angle opposite to equal sides of a triangle) $\ldots$ (5)
From equations (3), (4), and (5), we obtain
$\angle ACD=\angle BCD$.
In $\triangle CAD$ and $\triangle CBD$,
$\angle ACD=\angle BCD$ [Using equation (6)]
$\angle CDA=\angle CDB[.$ Both $90^{\circ}$ ]
Therefore, the remaining angles should be equal.
$\therefore \angle CAD=\angle CBD$
$\Rightarrow \angle A=\angle B$
Alternatively,
Let us consider a triangle $A B C$ in which $C D \perp A B$.

It is given that,
$\cos A=\cos B$
$\Rightarrow \dfrac{AD}{AC}=\dfrac{BD}{BC}$
$\Rightarrow \dfrac{AD}{BD}=\dfrac{AC}{BC}$
Let $\dfrac{AD}{BD}=\dfrac{AC}{BC}=k$
$\Rightarrow AD=k BD$.
And, $AC=k BC$
Using Pythagoras theorem for triangles CAD and CBD, we obtain
$C D^{2}=A C^{2}-A D^{2}$..
And, $CD^{2}=BC^{2}-BD^{2}$.
From equations (3) and (4), we obtain
$A C^{2}-A D^{2}=B C^{2}-B D^{2}$
$\Rightarrow(k B C)^{2}-(k B D)^{2}=BC^{2}-BD^{2}$
$\Rightarrow k^{2}(BC^{2}-BD^{2})=BC^{2}-BD^{2}$
$\Rightarrow k^{2}=1$
$\Rightarrow k=1$
Putting this value in equation (2), we obtain
$AC=BC$
$\Rightarrow \angle A=\angle B$ (Angles opposite to equal sides of a triangle)
7. If $\cot \theta=\dfrac{7}{8}$, evaluate :
(i) $\dfrac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$,
(ii) $\cot ^{2} \theta$
Show Answer
Solution
Let us consider a right triangle $A B C$, right-angled at point $B$.

$ \begin{aligned} \cot \theta & =\dfrac{\text{ Side adjacent to } \angle \theta}{\text{ Side opposite to } \angle \theta}=\dfrac{BC}{AB} \\ & =\dfrac{7}{8} \end{aligned} $
If $BC$ is $7 k$, then $AB$ will be $8 k$, where $k$ is a positive integer.
Applying Pythagoras theorem in $\triangle A B C$, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$=(8 k)^{2}+(7 k)^{2}$
$=64 k^{2}+49 k^{2}$
$=113 k^{2}$
$AC=\sqrt{113} k$
$\sin \theta=\dfrac{\text{ Side opposite to } \angle \theta}{\text{ Hypotenuse }}=\dfrac{AB}{AC}$
$=\dfrac{8 k}{\sqrt{113} k}=\dfrac{8}{\sqrt{113}}$
$\cos \theta=\dfrac{\text{ Side adjacent to } \angle \theta}{\text{ Hypotenuse }}=\dfrac{BC}{AC}$
$=\dfrac{7 k}{\sqrt{113} k}=\dfrac{7}{\sqrt{113}}$
(i) $\dfrac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\dfrac{(1-\sin ^{2} \theta)}{(1-\cos ^{2} \theta)}$ $=\dfrac{1-(\dfrac{8}{\sqrt{113}})^{2}}{1-(\dfrac{7}{\sqrt{113}})^{2}}=\dfrac{1-\dfrac{64}{113}}{1-\dfrac{49}{113}}$
$=\dfrac{\dfrac{49}{113}}{64}=\dfrac{49}{64}$
113
(ii) $\cot ^{2} \theta=(\cot \theta)^{2}=(\dfrac{7}{8})^{2}=\dfrac{49}{64}$
8. If $3 \cot A=4$, check whether $\dfrac{1-\tan ^{2} A}{1+\tan ^{2} A}=\cos ^{2} A-\sin ^{2} A$ or not.
Show Answer
Solution
It is given that $3 \cot A=4$
Or, $\cot A=\dfrac{4}{3}$
Consider a right triangle $A B C$, right-angled at point $B$.

$\cot A=\dfrac{\text{ Side adjacent to } \angle A}{\text{ Side opposite to } \angle A}$
$\dfrac{AB}{BC}=\dfrac{4}{3}$
If $AB$ is $4 k$, then $BC$ will be $3 k$, where $k$ is a positive integer.
In $\triangle ABC$,
$(A C)^{2}=(A B)^{2}+(B C)^{2}$
$=(4 k)^{2}+(3 k)^{2}$
$ \begin{aligned} & =16 k^{2}+9 k^{2} \\ & =25 k^{2} \\ & A C=5 k \\ & \cos A=\dfrac{\text{ Side adjacent to } \angle A}{\text{ Hypotenuse }}=\dfrac{AB}{AC} \\ & =\dfrac{4 k}{5 k}=\dfrac{4}{5} \\ & \sin A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Hypotenuse }}=\dfrac{BC}{AC} \\ & =\dfrac{3 k}{5 k}=\dfrac{3}{5} \\ & \tan A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Hypotenuse }}=\dfrac{BC}{AB} \\ & =\dfrac{3 k}{4 k}=\dfrac{3}{4} \\ & \dfrac{1-\tan ^{2} A}{1+\tan ^{2} A}=\dfrac{1-(\dfrac{3}{4})^{2}}{1+(\dfrac{3}{4})^{2}}=\dfrac{1-\dfrac{9}{16}}{1+\dfrac{9}{16}} \\ & =\dfrac{\dfrac{7}{16}}{\dfrac{25}{16}}=\dfrac{7}{25} \\ & \cos ^{2} A-\sin ^{2} A=(\dfrac{4}{5})^{2}-(\dfrac{3}{5})^{2} \\ & =\dfrac{16}{25}-\dfrac{9}{25}=\dfrac{7}{25} \\ & \therefore \dfrac{1-\tan ^{2} A}{1+\tan ^{2} A}=\cos ^{2} A-\sin ^{2} A \end{aligned} $
9. In triangle $A B C$, right-angled at $B$, if $\tan A=\dfrac{1}{\sqrt{3}}$, find the value of:
(i) $\sin A \cos C+\cos A \sin C$
(ii) $\cos A \cos C-\sin A \sin C$
Show Answer
Solution

$\tan A=\dfrac{1}{\sqrt{3}}$
$\dfrac{BC}{AB}=\dfrac{1}{\sqrt{3}}$
If $BC$ is $k$, then $AB$ will be $\sqrt{3} k$, where $k$ is a positive integer.
In $\triangle ABC$,
$A C^{2}=A B^{2}+BC^{2}$
$=(\sqrt{3} k)^{2}+(k)^{2}$
$=3 k^{2}+k^{2}=4 k^{2}$
$\therefore AC=2 k$
$\sin A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Hypotenuse }}=\dfrac{BC}{AC}=\dfrac{k}{2 k}=\dfrac{1}{2}$
$\cos A=\dfrac{\text{ Side adjacent to } \angle A}{\text{ Hypotenuse }}=\dfrac{AB}{AC}=\dfrac{\sqrt{3} k}{2 k}=\dfrac{\sqrt{3}}{2}$
$\sin C=\dfrac{\text{ Side opposite to } \angle C}{\text{ Hypotenuse }}=\dfrac{AB}{AC}=\dfrac{\sqrt{3} k}{2 k}=\dfrac{\sqrt{3}}{2}$
$\cos C=\dfrac{\text{ Side adjacent to } \angle C}{\text{ Hypotenuse }}=\dfrac{BC}{AC}=\dfrac{k}{2 k}=\dfrac{1}{2}$
(i) $\sin A \cos C+\cos A \sin C$
$ \begin{aligned} & =(\dfrac{1}{2})(\dfrac{1}{2})+(\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{3}}{2})=\dfrac{1}{4}+\dfrac{3}{4} \\ & =\dfrac{4}{4}=1 \end{aligned} $
(ii) $\cos A \cos C-\sin A \sin C$ $=(\dfrac{\sqrt{3}}{2})(\dfrac{1}{2})-(\dfrac{1}{2})(\dfrac{\sqrt{3}}{2})=\dfrac{\sqrt{3}}{4}-\dfrac{\sqrt{3}}{4}=0$
10. In $\Delta PQR$, right- angled at $Q, PR+QR=25 cm$ and $PQ=5 cm$. Determine the values of sin $P, \cos P$ and $\tan P$.
Show Answer
Solution
Given that, $PR+QR=25$
$PQ=5$
Let PR be $x$.
Therefore, $QR=25-x$

Applying Pythagoras theorem in $\triangle PQR$, we obtain
$PR^{2}=PQ^{2}+QR^{2}$
$x^{2}=(5)^{2}+(25-x)^{2}$
$x^{2}=25+625+x^{2}-50 x$
$50 x=650$
$x=13$
Therefore, $PR=13 cm$
$QR=(25-13) cm=12 cm$
$\sin P=\dfrac{\text{ Side opposite to } \angle P}{\text{ Hypotenuse }}=\dfrac{QR}{PR}=\dfrac{12}{13}$
$\cos P=\dfrac{\text{ Side adjacent to } \angle P}{\text{ Hypotenuse }}=\dfrac{PQ}{PR}=\dfrac{5}{13}$
$\tan P=\dfrac{\text{ Side opposite to } \angle P}{\text{ Side adjacent to } \angle P}=\dfrac{QR}{PQ}=\dfrac{12}{5}$
11. State whether the following are true or false. Justify your answer.
(i) The value of $\tan A$ is always less than 1.
(ii) sec $A=\dfrac{12}{5}$ for some value of angle $A$.
(iii) $\cos A$ is the abbreviation used for the cosecant of angle $A$.
(iv) $\cot A$ is the product of cot and $A$.
(v) $\sin \theta=\dfrac{4}{3}$ for some angle $\theta$.
Show Answer
Solution
(i) Consider a $\triangle A B C$, right-angled at $B$.

$\tan A=\dfrac{\text{ Side opposite to } \angle A}{\text{ Side adjacent to } \angle A}$
$=\dfrac{12}{5}$
But $\dfrac{12}{5}>1$
$\therefore \tan A>1$
So, $\tan A<1$ is not always true.
Hence, the given statement is false.
(ii)
$ \sec A=\dfrac{12}{5} $

$\dfrac{\text{ Hypotenuse }}{\text{ Side adjacent to } \angle A}=\dfrac{12}{5}$
$\dfrac{AC}{AB}=\dfrac{12}{5}$
Let $A C$ be $12 k, A B$ will be $5 k$, where $k$ is a positive integer.
Applying Pythagoras theorem in $\triangle ABC$, we obtain
$A C^{2}=A B^{2}+B C^{2}$
$(12 k)^{2}=(5 k)^{2}+BC^{2}$
$144 k^{2}=25 k^{2}+BC^{2}$
$BC^{2}=119 k^{2}$
$BC=10.9 k$
It can be observed that for given two sides $AC=12 k$ and $AB=5 k$,
$B C$ should be such that,
$A C-A B<B C<A C+A B$
$12 k-5 k<BC<12 k+5 k$
$7 k<BC<17 k$
However, $BC=10.9 k$. Clearly, such a triangle is possible and hence, such value of sec $A$ is possible.
Hence, the given statement is true.
(iii) Abbreviation used for cosecant of angle $A$ is $cosec A$. And $\cos A$ is the abbreviation used for cosine of angle $A$.
Hence, the given statement is false.
(iv) $\cot A$ is not the product of $\cot$ and $A$. It is the cotangent of $\angle A$.
Hence, the given statement is false.
(v) $\sin \theta=\dfrac{4}{3}$
We know that in a right-angled triangle,
$ \sin \theta=\dfrac{\text{ Side opposite to } \angle \theta}{\text{ Hypotenuse }} $
In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of $\sin \theta$ is not possible.
Hence, the given statement is false
8.3 Trigonometric Ratios of Some Specific Angles
From geometry, you are already familiar with the construction of angles of $30^{\circ}, 45^{\circ}$, $60^{\circ}$ and $90^{\circ}$. In this section, we will find the values of the trigonometric ratios for these angles and, of course, for $0^{\circ}$.
Trigonometric Ratios of $45^{\circ}$
In $\triangle ABC$, right-angled at $B$, if one angle is $45^{\circ}$, then the other angle is also $45^{\circ}$, i.e., $\angle A=\angle C=45^{\circ}$ (see Fig. 8.14).

Fig. 8.14
So,
$ BC=AB \quad(\text{ Why? }) $
Now, Suppose $BC=AB=a$.
Then by Pythagoras Theorem, $AC^{2}=AB^{2}+BC^{2}=a^{2}+a^{2}=2 a^{2}$,
and, therefore, $\quad AC=a \sqrt{2}$.
Using the definitions of the trigonometric ratios, we have :
$ \begin{aligned} & \sin 45^{\circ}=\dfrac{\text{ side opposite to angle } 45^{\circ}}{\text{ hypotenuse }}=\dfrac{BC}{AC}=\dfrac{a}{a \sqrt{2}}=\dfrac{1}{\sqrt{2}} \\ & \cos 45^{\circ}=\dfrac{\text{ side adjacent to angle } 45^{\circ}}{\text{ hypotenuse }}=\dfrac{AB}{AC}=\dfrac{a}{a \sqrt{2}}=\dfrac{1}{\sqrt{2}} \\ & \tan 45^{\circ}=\dfrac{\text{ side opposite to angle } 45^{\circ}}{\text{ side adjacent to angle } 45^{\circ}}=\dfrac{BC}{AB}=\dfrac{a}{a}=1 \end{aligned} $
Also, $cosec 45^{\circ}=\dfrac{1}{\sin 45^{\circ}}=\sqrt{2}, \sec 45^{\circ}=\dfrac{1}{\cos 45^{\circ}}=\sqrt{2}, \cot 45^{\circ}=\dfrac{1}{\tan 45^{\circ}}=1$.
Trigonometric Ratios of $30^{\circ}$ and $60^{\circ}$
Let us now calculate the trigonometric ratios of $30^{\circ}$ and $60^{\circ}$. Consider an equilateral triangle $ABC$. Since each angle in an equilateral triangle is $60^{\circ}$, therefore, $\angle A=\angle B=\angle C=60^{\circ}$.
Draw the perpendicular $AD$ from $A$ to the side $BC$ (see Fig. 8.15).

Fig. 8.15
$ \begin{aligned} \text{Now } \quad \quad \quad & \Delta ABD \cong \Delta ACD \quad(\text{ Why? }) \\ \text{Therefore, } \quad \quad \quad & BD =DC \\ \text{ and } \quad \quad \quad & \angle BAD =\angle CAD \quad(CPCT) \end{aligned} $
Now observe that:
$\triangle ABD$ is a right triangle, right- angled at $D$ with $\angle BAD=30^{\circ}$ and $\angle ABD=60^{\circ}$ (see Fig. 8.15).
As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that $AB=2 a$.
Then, $ BD=\dfrac{1}{2} BC=a $
and $ AD^{2}=AB^{2}-BD^{2}=(2 a)^{2}-(a)^{2}=3 a^{2}, $
Therefore, $ AD=a \sqrt{3} $
Now, we have : $ \begin{aligned} & \sin 30^{\circ}=\dfrac{BD}{AB}=\dfrac{a}{2 a}=\dfrac{1}{2}, \cos 30^{\circ}=\dfrac{AD}{AB}=\dfrac{a \sqrt{3}}{2 a}=\dfrac{\sqrt{3}}{2} \\ & \tan 30^{\circ}=\dfrac{BD}{AD}=\dfrac{a}{a \sqrt{3}}=\dfrac{1}{\sqrt{3}} . \end{aligned} $
Also, $\quad cosec 30^{\circ}=\dfrac{1}{\sin 30^{\circ}}=2, \quad \sec 30^{\circ}=\dfrac{1}{\cos 30^{\circ}}=\dfrac{2}{\sqrt{3}}$
$$ \cot 30^{\circ}=\dfrac{1}{\tan 30^{\circ}}=\sqrt{3} . $$
Similarly, $ \begin{aligned} \sin 60^{\circ} & =\dfrac{AD}{AB}=\dfrac{a \sqrt{3}}{2 a}=\dfrac{\sqrt{3}}{2}, \cos 60^{\circ}=\dfrac{1}{2}, \tan 60^{\circ}=\sqrt{3}, \\ \text{cosec} 60^{\circ} & =\dfrac{2}{\sqrt{3}}, \sec 60^{\circ}=2 \text{ and } \cot 60^{\circ}=\dfrac{1}{\sqrt{3}} . \end{aligned} $
Trigonometric Ratios of $0^{\circ}$ and $\mathbf{9 0}$
Let us see what happens to the trigonometric ratios of angle $A$, if it is made smaller and smaller in the right triangle $ABC$ (see Fig. 8.16), till it becomes zero. As $\angle$ A gets smaller and smaller, the length of the side $BC$ decreases. The point $C$ gets closer to point $B$, and finally when $\angle A$ becomes very close to $0^{\circ}, AC$ becomes almost the same as $AB$ (see Fig. 8.17).

Fig. 8.16

Fig. 8.17
When $\angle A$ is very close to $0^{\circ}, BC$ gets very close to 0 and so the value of $\sin A=\dfrac{BC}{AC}$ is very close to 0 . Also, when $\angle A$ is very close to $0^{\circ}, AC$ is nearly the same as $A B$ and so the value of $\cos A=\dfrac{A B}{A C}$ is very close to 1 .
This helps us to see how we can define the values of sin A and $\cos A$ when $A=0^{\circ}$. We define : $\boldsymbol{{}\operatorname { s i n }} \mathbf{0}^{\circ}=\mathbf{0}$ and $\cos \mathbf{0}^{\circ}=\mathbf{1}$.
Using these, we have :
$\tan 0^{\circ}=\dfrac{\sin 0^{\circ}}{\cos 0^{\circ}}=0, \cot 0^{\circ}=\dfrac{1}{\tan 0^{\circ}}$, which is not defined. (Why?)
sec $0^{\circ}=\dfrac{1}{\cos 0^{\circ}}=1$ and $cosec 0^{\circ}=\dfrac{1}{\sin 0^{\circ}}$, which is again not defined.(Why?)
Now, let us see what happens to the trigonometric ratios of $\angle A$, when it is made larger and larger in $\triangle ABC$ till it becomes $90^{\circ}$. As $\angle A$ gets larger and larger, $\angle C$ gets smaller and smaller. Therefore, as in the case above, the length of the side $A B$ goes on decreasing. The point $A$ gets closer to point $B$. Finally when $\angle A$ is very close to $90^{\circ}$, $\angle C$ becomes very close to $0^{\circ}$ and the side $AC$ almost coincides with side $BC$ (see Fig. 8.18).

Fig. 8.18
When $\angle C$ is very close to $0^{\circ}, \angle A$ is very close to $90^{\circ}$, side $AC$ is nearly the same as side $BC$, and so sin $A$ is very close to 1 . Also when $\angle A$ is very close to $90^{\circ}$, $\angle C$ is very close to $0^{\circ}$, and the side $AB$ is nearly zero, so cos $A$ is very close to 0 .
So, we define :
$ \sin 90^{\circ}=1 \text{ and } \cos 90^{\circ}=0 . $
Now, why don’t you find the other trigonometric ratios of $90^{\circ}$ ?
We shall now give the values of all the trigonometric ratios of $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ and $90^{\circ}$ in Table 8.1, for ready reference.
Table 8.1
| $\angle \mathbf{A}$ | $\mathbf{0}^{\circ}$ | $\mathbf{3 0}^{\circ}$ | $\mathbf{4 5}^{\circ}$ | $\mathbf{6 0}^{\circ}$ | $\mathbf{9 0}^{\circ}$ |
|---|---|---|---|---|---|
| $\sin A$ | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{\sqrt{3}}{2}$ | 1 |
| $\cos A$ | 1 | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{2}$ | 0 |
| $\tan A$ | 0 | $\dfrac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | Not defined |
| $\operatorname{cosec~A}$ | Not defined | 2 | $\sqrt{2}$ | $\dfrac{2}{\sqrt{3}}$ | 1 |
| $\sec A$ | 1 | $\dfrac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | Not defined |
| $\cot A$ | Not defined | $\sqrt{3}$ | 1 | $\dfrac{1}{\sqrt{3}}$ | 0 |
Remark : From the table above you can observe that as $\angle A$ increases from $0^{\circ}$ to $90^{\circ}$, sin A increases from 0 to 1 and cos A decreases from 1 to 0 .
Let us illustrate the use of the values in the table above through some examples.
Example 6 : In $\triangle ABC$, right-angled at $B$, $AB=5 ~cm$ and $\angle ACB=30^{\circ}$ (see Fig. 8.19). Determine the lengths of the sides $BC$ and $AC$.

Fig. 8.19
Solution : To find the length of the side $BC$, we will choose the trigonometric ratio involving $BC$ and the given side $A B$. Since $B C$ is the side adjacent to angle $C$ and $AB$ is the side opposite to angle $C$, therefore
$ \dfrac{AB}{BC}=\tan C $
i.e., $ \dfrac{5}{BC}=\tan 30^{\circ}=\dfrac{1}{\sqrt{3}} $
which gives $ BC=5 \sqrt{3} cm $
To find the length of the side AC, we consider
$ \begin{aligned} & \sin 30^{\circ} =\dfrac{AB}{AC} \quad \quad \quad \text{(Why?)} \\ \text{ i.e., }\quad \quad \quad & \dfrac{1}{2} =\dfrac{5}{AC} \\ \text{ i.e., }\quad \quad \quad & AC =10 ~cm \end{aligned} $
Note that alternatively we could have used Pythagoras theorem to determine the third side in the example above,
i.e., $ A C=\sqrt{A B^{2}+B C^{2}}=\sqrt{5^{2}+(5 \sqrt{3})^{2}} cm=10 cm . $
Example 7 : In $\Delta PQR$, right-angled at $Q$ (see Fig. 8.20), PQ=3 cm and PR=6 cm. Determine $\angle QPR$ and $\angle PRQ$.

Fig. 8.20
Solution : Given PQ=3 cm and PR=6 cm.
Therefore, $ \dfrac{P Q}{P R}=\sin R $
or $ \sin R=\dfrac{3}{6}=\dfrac{1}{2} $
So, $ \angle PRQ=30^{\circ} $
and therefore, $ \angle QPR=60^{\circ} . \quad(\text{ Why? }) $
You may note that if one of the sides and any other part (either an acute angle or any side) of a right triangle is known, the remaining sides and angles of the triangle can be determined.
Example 8 : If $\sin (A-B)=\dfrac{1}{2}, \cos (A+B)=\dfrac{1}{2}, 0^{\circ}<A+B \leq 90^{\circ}, A>B$, find $A$ and B.
Solution : Since, $\sin (A-B)=\dfrac{1}{2}$, therefore, $A-B=30^{\circ} \quad($ Why? $) \quad \quad \quad \quad (1)$
Also, since $\cos (A+B)=\dfrac{1}{2}$, therefore, $A+B=60^{\circ} \quad$ (Why?) $\quad \quad \quad \quad (2)$
Solving (1) and (2), we get : $A=45^{\circ}$ and $B=15^{\circ}$.
EXERCISE 8.2
1. Evaluate the following:
(i) $\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}$
(ii) $2 \tan ^{2} 45^{\circ}+\cos ^{2} 30^{\circ}-\sin ^{2} 60^{\circ}$
(iii) $\dfrac{\cos 45^{\circ}}{\sec 30^{\circ}+cosec 30^{\circ}}$
(iv) $\dfrac{\sin 30^{\circ}+\tan 45^{\circ}-cosec 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}$
(v) $\dfrac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$
Show Answer
Solution
(i) $\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}$
$=(\dfrac{\sqrt{3}}{2})(\dfrac{\sqrt{3}}{2})+(\dfrac{1}{2})(\dfrac{1}{2})$
$=\dfrac{3}{4}+\dfrac{1}{4}=\dfrac{4}{4}=1$
(ii) $2 \tan ^{2} 45^{\circ}+\cos ^{2} 30^{\circ}-\sin ^{2} 60^{\circ}$
$=2(1)^{2}+(\dfrac{\sqrt{3}}{2})^{2}-(\dfrac{\sqrt{3}}{2})^{2}$
$=2+\dfrac{3}{4}-\dfrac{3}{4}=2$
(iii) $\dfrac{\cos 45^{\circ}}{\sec 30^{\circ}+cosec 30^{\circ}}$
$ \begin{aligned} & =\dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2}{\sqrt{3}}+2}=\dfrac{\dfrac{1}{\sqrt{2}}}{\dfrac{2+2 \sqrt{3}}{\sqrt{3}}} \\ & =\dfrac{\sqrt{3}}{\sqrt{2}(2+2 \sqrt{3})}=\dfrac{\sqrt{3}}{2 \sqrt{2}+2 \sqrt{6}} \\ & =\dfrac{\sqrt{3}(2 \sqrt{6}-2 \sqrt{2})}{(2 \sqrt{6}+2 \sqrt{2})(2 \sqrt{6}-2 \sqrt{2})} \end{aligned} $
$=\dfrac{2 \sqrt{3}(\sqrt{6}-\sqrt{2})}{(2 \sqrt{6})^{2}-(2 \sqrt{2})^{2}}=\dfrac{2 \sqrt{3}(\sqrt{6}-\sqrt{2})}{24-8}=\dfrac{2 \sqrt{3}(\sqrt{6}-\sqrt{2})}{16}$
$=\dfrac{\sqrt{18}-\sqrt{6}}{8}=\dfrac{3 \sqrt{2}-\sqrt{6}}{8}$
$\dfrac{\sin 30^{\circ}+\tan 45^{\circ}-cosec 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}$
$=\dfrac{\dfrac{1}{2}+1-\dfrac{2}{\sqrt{3}}}{\dfrac{2}{\sqrt{3}}+\dfrac{1}{2}+1}=\dfrac{\dfrac{3}{2}-\dfrac{2}{\sqrt{3}}}{\dfrac{3}{2}+\dfrac{2}{\sqrt{3}}}$
$=\dfrac{\dfrac{3 \sqrt{3}-4}{2 \sqrt{3}}}{\dfrac{3 \sqrt{3}+4}{2 \sqrt{3}}}=\dfrac{(3 \sqrt{3}-4)}{(3 \sqrt{3}+4)}$
$=\dfrac{(3 \sqrt{3}-4)(3 \sqrt{3}-4)}{(3 \sqrt{3}+4)(3 \sqrt{3}-4)}=\dfrac{(3 \sqrt{3}-4)^{2}}{(3 \sqrt{3})^{2}-(4)^{2}}$
$=\dfrac{27+16-24 \sqrt{3}}{27-16}=\dfrac{43-24 \sqrt{3}}{11}$
(v) $\dfrac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$
$ \begin{aligned} & =\dfrac{5(\dfrac{1}{2})^{2}+4(\dfrac{2}{\sqrt{3}})^{2}-(1)^{2}}{(\dfrac{1}{2})^{2}+(\dfrac{\sqrt{3}}{2})^{2}} \\ & =\dfrac{5(\dfrac{1}{4})+(\dfrac{16}{3})-1}{\dfrac{1}{4}+\dfrac{3}{4}} \\ & =\dfrac{\dfrac{15+64-12}{12}}{\dfrac{4}{4}}=\dfrac{67}{12} \end{aligned} $
2. Choose the correct option and justify your choice :
(i) $\dfrac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}=$
(A) $\sin 60^{\circ}$
(B) $\cos 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
(ii) $\dfrac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=$
(A) $\tan 90^{\circ}$
(B) 1
(C) $\sin 45^{\circ}$
(D) 0
(iii) $\sin 2 A=2 \sin A$ is true when $A=$
(A) $0^{\circ}$
(B) $30^{\circ}$
(C) $45^{\circ}$
(D) $60^{\circ}$
(iv) $\dfrac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}=$
(A) $\cos 60^{\circ}$
(B) $\sin 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
Show Answer
Solution
(i) $\dfrac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}$
$=\dfrac{2(\dfrac{1}{\sqrt{3}})}{1+(\dfrac{1}{\sqrt{3}})^{2}}=\dfrac{\dfrac{2}{\sqrt{3}}}{1+\dfrac{1}{3}}=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{4}{3}}$
$=\dfrac{6}{4 \sqrt{3}}=\dfrac{\sqrt{3}}{2}$
Out of the given alternatives, only
$ \sin 60^{\circ}=\dfrac{\sqrt{3}}{2} $
Hence, (A) is correct.
(ii) $\dfrac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}$
$=\dfrac{1-(1)^{2}}{1+(1)^{2}}=\dfrac{1-1}{1+1}=\dfrac{0}{2}=0$
Hence, (D) is correct.
(iii)Out of the given alternatives, only $A=0^{\circ}$ is correct.
As $\sin 2 A=\sin 0^{\circ}=0$
$2 \sin A=2 \sin 0^{\circ}=2(0)=0$
Hence, $(A)$ is correct.
(iv) $\dfrac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}$
$=\dfrac{2(\dfrac{1}{\sqrt{3}})}{1-(\dfrac{1}{\sqrt{3}})^{2}}=\dfrac{\dfrac{2}{\sqrt{3}}}{1-\dfrac{1}{3}}=\dfrac{\dfrac{2}{\sqrt{3}}}{\dfrac{2}{3}}$
$=\sqrt{3}$
Out of the given alternatives, only $\tan 60^{\circ}=\sqrt{3}$
Hence, (C) is correct.
3. If $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\dfrac{1}{\sqrt{3}} ; 0^{\circ}<A+B \leq 90^{\circ} ; A>B$, find $A$ and $B$.
Show Answer
Solution
$\tan (A+B)=\sqrt{3}$
$\Rightarrow \tan (A+B)=\tan 60$
$\Rightarrow A+B=60 \ldots$ (1)
$\tan (A-B)=\dfrac{1}{\sqrt{3}}$
$\Rightarrow \tan (A-B)=\tan 30$
$\Rightarrow A-B=30$..
On adding both equations, we obtain
$2 A=90$
$\Rightarrow A=45$
From equation (1), we obtain
$45+B=60$
$B=15$
Therefore, $\angle A=45^{\circ}$ and $\angle B=15^{\circ}$
4. State whether the following are true or false. Justify your answer.
(i) $\sin (A+B)=\sin A+\sin B$.
(ii) The value of $\sin \theta$ increases as $\theta$ increases.
(iii) The value of $\cos \theta$ increases as $\theta$ increases.
(iv) $\sin \theta=\cos \theta$ for all values of $\theta$.
(v) $\cot A$ is not defined for $A=0^{\circ}$.
Show Answer
Solution
(i) $\sin (A+B)=\sin A+\sin B$
Let $A=30^{\circ}$ and $B=60^{\circ}$
$\sin (A+B)=\sin (30^{\circ}+60^{\circ})$
$=\sin 90^{\circ}$
$=1$
$\sin A+\sin B=\sin 30^{\circ}+\sin 60^{\circ}$
$=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}=\dfrac{1+\sqrt{3}}{2}$
Clearly, $\sin (A+B) \neq \sin A+\sin B$
Hence, the given statement is false.
(ii) The value of $\sin \theta$ increases as $\theta$ increases in the interval of $0^{\circ}<\theta<90^{\circ}$ as
$\sin 0^{\circ}=0$
$\sin 30^{\circ}=\dfrac{1}{2}=0.5$
$\sin 45^{\circ}=\dfrac{1}{\sqrt{2}}=0.707$
$\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}=0.866$
$\sin 90^{\circ}=1$
Hence, the given statement is true.
(iii) $\cos 0^{\circ}=1$
$\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}=0.866$
$\cos 45^{\circ}=\dfrac{1}{\sqrt{2}}=0.707$
$\cos 60^{\circ}=\dfrac{1}{2}=0.5$
$\cos 90^{\circ}=0$
It can be observed that the value of $\cos \theta$ does not increase in the interval of $0^{\circ}<\theta<90^{\circ}$.
Hence, the given statement is false.
(iv) $\sin \theta=\cos \theta$ for all values of $\theta$.
This is true when $\theta=45^{\circ}$
$ \begin{aligned} & \sin 45^{\circ}=\dfrac{1}{\sqrt{2}} \\ & \text{ As } \\ & \cos 45^{\circ}=\dfrac{1}{\sqrt{2}} \end{aligned} $
It is not true for all other values of $\theta$.
As $\sin 30^{\circ}=\dfrac{1}{2}$ and $\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$,
Hence, the given statement is false.
(v) $\cot A$ is not defined for $A=0^{\circ}$
$ \begin{aligned} & \text{ As } \cot A=\dfrac{\cos A}{\sin A} \\ & \cot 0^{\circ}=\dfrac{\cos 0^{\circ}}{\sin 0^{\circ}}=\dfrac{1}{0}=\text{ undefined } \end{aligned} $
Hence, the given statement is true.
8.4 Trigonometric Identities
You may recall that an equation is called an identity when it is true for all values of the variables involved. Similarly, an equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.
In this section, we will prove one trigonometric identity, and use it further to prove other useful trigonometric identities.
In $\triangle ABC$, right-angled at $B$ (see Fig. 8.21), we have:
$ AB^{2}+BC^{2}=AC^{2} \tag{1} $

Fig. 8.21
Dividing each term of (1) by $AC^{2}$, we get
$ \dfrac{AB^{2}}{AC^{2}}+\dfrac{BC^{2}}{AC}=\dfrac{AC^{2}}{A C^{2}} $
i.e., $ (\dfrac{AB}{AC})^{2}+(\dfrac{BC}{AC})^{2}=(\dfrac{AC}{AC})^{2} $
i.e., $ (\cos A)^{2}+(\sin A)^{2}=1 $
i.e., $ \cos ^{2} A+\sin ^{2} A=1 \tag{2} $
This is true for all A such that $0^{\circ} \leq A \leq 90^{\circ}$. So, this is a trigonometric identity.
Let us now divide (1) by $AB^{2}$. We get
$ \dfrac{AB^{2}}{AB^{2}}+\dfrac{BC^{2}}{AB^{2}}=\dfrac{AC^{2}}{AB^{2}} $
or, $ (\dfrac{AB}{AB})^{2}+(\dfrac{BC}{AB})^{2}=(\dfrac{AC}{AB})^{2} $
$ \text{ i.e., } \quad 1+\tan ^{2} A=\sec ^{2} A \tag{3} $
Is this equation true for $A=0^{\circ}$ ? Yes, it is. What about $A=90^{\circ}$ ? Well, $\tan A$ and sec $A$ are not defined for $A=90^{\circ}$. So, (3) is true for all A such that $0^{\circ} \leq A<90^{\circ}$.
Let us see what we get on dividing (1) by $BC^{2}$. We get
$ \dfrac{AB^{2}}{BC^{2}}+\dfrac{BC^{2}}{BC^{2}}=\dfrac{AC^{2}}{BC^{2}} $
$ \text{i.e.,} \quad \quad \quad(\dfrac{A B}{B C})^{2}+(\dfrac{B C}{B C})^{2}=(\dfrac{A C}{B C})^{2}$
$$\text{i.e.,} \quad \quad \quad \cot^{2} \mathbf{A}+1=cosec^{2} \mathbf{A} \tag{4}$$
Note that $\text{cosec} A$ and $\cot A$ are not defined for $A=0^{\circ}$. Therefore (4) is true for all A such that $0^{\circ}<A \leq 90^{\circ}$.
Using these identities, we can express each trigonometric ratio in terms of other trigonometric ratios, i.e., if any one of the ratios is known, we can also determine the values of other trigonometric ratios.
Let us see how we can do this using these identities. Suppose we know that $\tan A=\dfrac{1}{\sqrt{3}} \cdot$ Then, $\cot A=\sqrt{3}$.
Since, $\sec ^{2} A=1+\tan ^{2} A=1+\dfrac{1}{3}=\dfrac{4}{3}$, sec $A=\dfrac{2}{\sqrt{3}}$, and $\cos A=\dfrac{\sqrt{3}}{2}$.
Again, $\sin A=\sqrt{1-\cos ^{2} A}=\sqrt{1-\dfrac{3}{4}}=\dfrac{1}{2}$. Therefore, cosec $A=2$.
Example 9 : Express the ratios $\cos A$, $\tan A$ and sec $A$ in terms of $\sin A$.
Solution : Since
$ \cos ^{2} A+\sin ^{2} A=1 \text{, therefore, } $
$ \cos ^{2} A=1-\sin ^{2} A \text{, i.e., } \cos A= \pm \sqrt{1-\sin ^{2} A} $
This gives
$ \cos A=\sqrt{1-\sin ^{2} A} \quad \text{ (Why?) } $
Hence, $\quad \tan A=\dfrac{\sin A}{\cos A}=\dfrac{\sin A}{\sqrt{1-\sin ^{2} A}}$ and sec $A=\dfrac{1}{\cos A}=\dfrac{1}{\sqrt{1-\sin ^{2} A}}$
Example 10 : Prove that sec $A(1-\sin A)(\sec A+\tan A)=1$.
Solution :
LHS $=\sec A(1-\sin A)(\sec A+\tan A)=(\dfrac{1}{\cos A})(1-\sin A)(\dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A})$
$ \begin{aligned} & =\dfrac{(1-\sin A)(1+\sin A)}{\cos ^{2} A}=\dfrac{1-\sin ^{2} A}{\cos ^{2} A} \\ & =\dfrac{\cos ^{2} A}{\cos ^{2} A}=1=RHS \end{aligned} $
Example 11 : Prove that $\dfrac{\cot A-\cos A}{\cot A+\cos A}=\dfrac{cosec A-1}{cosec A+1}$
Solution : LHS $=\dfrac{\cot A-\cos A}{\cot A+\cos A}=\dfrac{\dfrac{\cos A}{\sin A}-\cos A}{\dfrac{\cos A}{\sin A}+\cos A}$
$ =\dfrac{\cos A(\dfrac{1}{\sin A}-1)}{\cos A(\dfrac{1}{\sin A}+1)}=\dfrac{(\dfrac{1}{\sin A}-1)}{(\dfrac{1}{\sin A}+1)}=\dfrac{cosec A-1}{cosec A+1}=\text{ RHS } $
Example 12 : Prove that $\dfrac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\dfrac{1}{\sec \theta-\tan \theta}$, using the identity $\sec ^{2} \theta=1+\tan ^{2} \theta$.
Solution : Since we will apply the identity involving sec $\theta$ and $\tan \theta$, let us first convert the LHS (of the identity we need to prove) in terms of sec $\theta$ and $\tan \theta$ by dividing numerator and denominator by $\cos \theta$.
$$ \begin{aligned} \text{ LHS } & =\dfrac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\dfrac{\tan \theta-1+\sec \theta}{\tan \theta+1-\sec \theta} \\ & =\dfrac{(\tan \theta+\sec \theta)-1}{(\tan \theta-\sec \theta)+1}=\dfrac{{(\tan \theta+\sec \theta)-1}(\tan \theta-\sec \theta)}{{(\tan \theta-\sec \theta)+1}(\tan \theta-\sec \theta)} \\ & =\dfrac{(\tan ^{2} \theta-\sec ^{2} \theta)-(\tan \theta-\sec \theta)}{{\tan \theta-\sec \theta+1}(\tan \theta-\sec \theta)} \\ & =\dfrac{-1-\tan \theta+\sec \theta}{(\tan \theta-\sec \theta+1)(\tan \theta-\sec \theta)} \\ & =\dfrac{-1}{\tan \theta-\sec \theta}=\dfrac{1}{\sec \theta-\tan \theta} \end{aligned} $$
which is the RHS of the identity, we are required to prove.
EXERCISE 8.3
1. Express the trigonometric ratios $\sin A, \sec A$ and $\tan A$ in terms of $\cot A$.
Show Answer
Solution
We know that,
$cosec^{2} A=1+\cot ^{2} A$
$\dfrac{1}{cosec^{2} A}=\dfrac{1}{1+\cot ^{2} A}$
$\sin ^{2} A=\dfrac{1}{1+\cot ^{2} A}$
$\sin A= \pm \dfrac{1}{\sqrt{1+\cot ^{2} A}}$
$\sqrt{1+\cot ^{2} A}$ will always be positive as we are adding two positive quantities.
Therefore, $\sin A=\dfrac{1}{\sqrt{1+\cot ^{2} A}}$
We know that, $\tan A=\dfrac{\sin A}{\cos A}$
However, $\cot A=\dfrac{\cos A}{\sin A}$
Therefore, $\tan A=\dfrac{1}{\cot A}$
Also, $\sec ^{2} A=1+\tan ^{2} A$
$=1+\dfrac{1}{\cot ^{2} A}$
$=\dfrac{\cot ^{2} A+1}{\cot ^{2} A}$
$\sec A=\dfrac{\sqrt{\cot ^{2} A+1}}{\cot A}$
2. Write all the other trigonometric ratios of $\angle A$ in terms of sec $A$.
Show Answer
Solution
We know that,
$\cos A=\dfrac{1}{\sec A}$
Also, $\sin ^{2} A+\cos ^{2} A=1$
$\sin ^{2} A=1-\cos ^{2} A$
$ \begin{aligned} \sin A & =\sqrt{1-(\dfrac{1}{\sec A})^{2}} \\ & =\sqrt{\dfrac{\sec ^{2} A-1}{\sec ^{2} A}}=\dfrac{\sqrt{\sec ^{2} A-1}}{\sec A} \end{aligned} $
$\tan ^{2} A+1=\sec ^{2} A$
$\tan ^{2} A=\sec ^{2} A-1$
$ \begin{aligned} \tan A & =\sqrt{\sec ^{2} A-1} \\ \cot A & =\dfrac{\cos A}{\sin A}=\dfrac{\dfrac{1}{\sec A}}{\dfrac{\sqrt{\sec ^{2} A-1}}{\sec A}} \\ & =\dfrac{1}{\sqrt{\sec ^{2} A-1}} \end{aligned} $
$cosec A=\dfrac{1}{\sin A}=\dfrac{\sec A}{\sqrt{\sec ^{2} A-1}}$
3. Choose the correct option. Justify your choice.
(i) $9 \sec ^{2} A-9 \tan ^{2} A=$
(A) 1
(B) 9
(C) 8
(D) 0
(ii) $(1+\tan \theta+\sec \theta)(1+\cot \theta-cosec \theta)=$
(A) 0
(B) 1
(C) 2
(D) -1
(iii) $(\sec A+\tan A)(1-\sin A)=$
(A) $\sec A$
(B) $\sin A$
(C) $cosec A$
(D) $\cos A$
(iv) $\dfrac{1+\tan ^{2} A}{1+\cot ^{2} A}=$
(A) $\sec ^{2} A$
(B) -1
(C) $\cot ^{2} A$
(D) $\tan ^{2} A$
Show Answer
Solution
(i) $9 \sec ^{2} A-9 \tan ^{2} A$
$=9(\sec ^{2} A-\tan ^{2} A)$
$=9$ (1) [As $.\sec ^{2} A-\tan ^{2} A=1]$
$=9$
Hence, alternative (B) is correct.
(ii)
$ \begin{aligned} & (1+\tan \theta+\sec \theta)(1+\cot \theta-cosec \theta) \\ & =(1+\dfrac{\sin \theta}{\cos \theta}+\dfrac{1}{\cos \theta})(1+\dfrac{\cos \theta}{\sin \theta}-\dfrac{1}{\sin \theta}) \\ & =(\dfrac{\cos \theta+\sin \theta+1}{\cos \theta})(\dfrac{\sin \theta+\cos \theta-1}{\sin \theta}) \\ & =\dfrac{(\sin \theta+\cos \theta)^{2}-(1)^{2}}{\sin \theta \cos \theta} \\ & =\dfrac{\sin \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta-1}{\sin \theta \cos \theta} \\ & =\dfrac{1+2 \sin \theta \cos \theta-1}{\sin \theta \cos \theta} \\ & =\dfrac{2 \sin \theta \cos \theta}{\sin \theta \cos \theta}=2 \end{aligned} $
Hence, alternative (C) is correct.
(iii) $(\sec A+\tan A)(1-\sin A)$
$ \begin{aligned} & =(\dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A})(1-\sin A) \\ & =(\dfrac{1+\sin A}{\cos A})(1-\sin A) \\ & =\dfrac{1-\sin ^{2} A}{\cos A}=\dfrac{\cos ^{2} A}{\cos A} \\ & =\cos A \end{aligned} $
Hence, alternative (D) is correct.
(iv)
$ \dfrac{1+\tan ^{2} A}{1+\cot ^{2} A}=\dfrac{1+\dfrac{\sin ^{2} A}{\cos ^{2} A}}{1+\dfrac{\cos ^{2} A}{\sin ^{2} A}} $
$ =\dfrac{\dfrac{\cos ^{2} A+\sin ^{2} A}{\cos ^{2} A}}{\dfrac{\sin ^{2} A+\cos ^{2} A}{\sin ^{2} A}}=\dfrac{\dfrac{1}{\cos ^{2} A}}{\dfrac{1}{\sin ^{2} A}} $
$=\dfrac{\sin ^{2} A}{\cos ^{2} A}=\tan ^{2} A$
Hence, alternative (D) is correct.
4. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
(i) $(cosec \theta-\cot \theta)^{2}=\dfrac{1-\cos \theta}{1+\cos \theta}$
(ii) $\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2 \sec A$
(iii) $\dfrac{\tan \theta}{1-\cot \theta}+\dfrac{\cot \theta}{1-\tan \theta}=1+\sec \theta cosec \theta$
[Hint : Write the expression in terms of $\sin \theta$ and $\cos \theta$ ]
(iv) $\dfrac{1+\sec A}{\sec A}=\dfrac{\sin ^2 A}{1-\cos A}$
[Hint : Simplify LHS and RHS separately]
(v) $\dfrac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec} A+\cot A$, wsing the identity $\operatorname{cosec}^2 A=1+\cot ^2 A$.
(vi) $\sqrt{\dfrac{1+\sin A}{1-\sin A}}=\sec A+\tan A$
(vii) $\dfrac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}=\tan \theta$
(viii) $(\sin \mathrm{A}+\operatorname{cosec} \mathrm{A})^2+(\cos \mathrm{A}+\sec \mathrm{A})^2=7+\tan ^2 \mathrm{~A}+\cot ^2 \mathrm{~A}$
(ix) $(\operatorname{cosec} A-\sin A)(\sec A-\cos A)=\dfrac{1}{\tan A+\cot A}$
[Hint : Simplify LHS and RHS separately]
(x) $\left(\dfrac{1+\tan ^2 A}{1+\cot ^2 A}\right)=\left(\dfrac{1-\tan A}{1-\cot A}\right)^2-\tan ^2 A$
Show Answer
Solution
(i)
$(cosec \theta-\cot \theta)^{2}=\dfrac{1-\cos \theta}{1+\cos \theta}$
L.H.S. $=(cosec \theta-\cot \theta)^{2}$
$=(\dfrac{1}{\sin \theta}-\dfrac{\cos \theta}{\sin \theta})^{2}$
$=\dfrac{(1-\cos \theta)^{2}}{(\sin \theta)^{2}}=\dfrac{(1-\cos \theta)^{2}}{\sin ^{2} \theta}$
$=\dfrac{(1-\cos \theta)^{2}}{1-\cos ^{2} \theta}=\dfrac{(1-\cos \theta)^{2}}{(1-\cos \theta)(1+\cos \theta)}=\dfrac{1-\cos \theta}{1+\cos \theta}$
$=$ R.H.S.
(ii)
$\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}=2 \sec A$
L.H.S. $=\dfrac{\cos A}{1+\sin A}+\dfrac{1+\sin A}{\cos A}$
$=\dfrac{\cos ^{2} A+(1+\sin A)^{2}}{(1+\sin A)(\cos A)}$
$=\dfrac{\cos ^{2} A+1+\sin ^{2} A+2 \sin A}{(1+\sin A)(\cos A)}$
$=\dfrac{\sin ^{2} A+\cos ^{2} A+1+2 \sin A}{(1+\sin A)(\cos A)}$
$=\dfrac{1+1+2 \sin A}{(1+\sin A)(\cos A)}=\dfrac{2+2 \sin A}{(1+\sin A)(\cos A)}$
$=\dfrac{2(1+\sin A)}{(1+\sin A)(\cos A)}=\dfrac{2}{\cos A}=2 \sec A$
$=$ R.H.S.
(iii) $\dfrac{\tan \theta}{1-\cot \theta}+\dfrac{\cot \theta}{1-\tan \theta}=1+\sec \theta cosec \theta$
$ \begin{aligned} \text{ L.H.S. } & =\dfrac{\tan \theta}{1-\cot \theta}+\dfrac{\cot \theta}{1-\tan \theta} \\ & =\dfrac{\dfrac{\sin \theta}{\cos \theta}}{1-\dfrac{\cos \theta}{\sin \theta}}+\dfrac{\dfrac{\cos \theta}{\sin \theta}}{1-\dfrac{\sin \theta}{\cos \theta}} \\ & =\dfrac{\dfrac{\cos \theta}{\cos \theta - \sin \theta}}{\cos \theta} by \dfrac{\dfrac{\cos \theta}{\sin \theta}{\cos \theta - \sin \theta}}{\cos \theta}\\ = & \dfrac{\sin ^{2} \theta}{\cos \theta(\sin ^{2} \theta-\cos \theta)}-\dfrac{\cos ^{2} \theta}{\sin ^{2} \theta(\sin \theta-\cos \theta)} \end{aligned} $
(iv)
By LHS
$\begin{aligned} & =\dfrac{\dfrac{1}{1}+\dfrac{1}{\cos A}}{\dfrac{1}{\cos A}} \\ \\ & =\frac{\frac{\cos A+1}{\cos A}}{\frac{1}{\cos A}}\\ \\ & =\cos A+1 \\ & =1+\cos A \\ \end{aligned}$
By RHS
$=\dfrac{1^2 -\cos ^2 A}{1-\cos A}$
$ \begin{array}{l} \because a^2-b^2=(a+b)(a-b) \\ \sin ^2 A+\cos ^2 A=1 \\ \sin ^2 A=1-\cos ^2 A \\ \end{array}$
$=\dfrac{(1+\cos A) (1-\cos A)} {(1-\cos A)}$
$1+\cos A$
LHS $=$ RHS
(v)
By LHS
$\text { Divide each term by } \sin \mathrm{A}$
$\begin{aligned} & =\dfrac{\dfrac{\cos A}{\sin A}-\dfrac{\sin A 1}{\sin A}+\dfrac{1}{\sin A}} {\dfrac{\cos A}{\sin A}+\dfrac{\sin A 1}{\sin A}-\dfrac{1}{\sin A}} \\ \\ & =\dfrac{\cot A-1+\operatorname{cosec} A}{\cot A+1-\operatorname{cosec} A} \\ \\ & =\frac{\cot A+\operatorname{cosec} A-\left(\operatorname{cosec}^2 A-\cot ^2 A\right)}{\cot A+1-\operatorname{cosec} A} \\ \\ & =\dfrac{\cot A+\operatorname{cosec} A-(\operatorname{cosec} A-\cot A)(\operatorname{cosec} A+\cot A)}{\cot A+1-\operatorname{cosec} A} \\ \\ & =\dfrac{\cot A+\operatorname{cosec} A[1-(\operatorname{cosec} A+\cot A)]}{\cot A+1-\operatorname{cosec} A} \\ \\ & =\dfrac{\cot A+\operatorname{cosec} A(1-\operatorname{cosec} A+\cot A)}{\cot A+1-\operatorname{cosec} A} \\ \\ & =\cot A+\operatorname{cosec} A \\ \\ & =\operatorname{cosec} A+\cot A &\end{aligned}$
= RHS
(vi)
By LHS
$\begin{aligned} & =\sqrt{\dfrac{(1+\sin A) \times(1+\sin A)}{(1-\sin A) \times(1+\sin A)}} \\ \\ & =\sqrt{\dfrac{(1+\sin A)^2}{1^2-\sin ^2 A}} \\ \\ & =\sqrt{\dfrac{(1+\sin A)^2}{\cos ^2 A}} \\ \\ & =\dfrac{\sqrt{(1+\sin A)^2}}{\sqrt{\cos^2 A}} \\ \\ & =\dfrac{1+\sin A}{\cos A} \\ \\ & \because (a-b)(a+b)=a^2-b^2 \\ \\ & \sin ^2 A+\cos ^2 A=1 \\ \\ & \cos ^2 A=1-\sin ^2 A \\ \\ & =\dfrac{1}{\cos A}+\dfrac{\sin A}{\cos A} \\ \\ & =\sec A+\tan A \end{aligned}$
= RHS Hence proved
(vii)
By LHS
$\begin{aligned} &= \dfrac{\sin \theta\left(1-2 \sin ^2 \theta\right)}{\cos \theta\left(2 \cos ^2 \theta-1\right)} \\ \\ &=\dfrac{\sin \theta\left(\sin ^2 \theta+\cos ^2 \theta-2 \sin ^2 \theta\right)}{\cos \theta\left(2 \cos ^2 \theta-\left(\sin ^2 \theta+\cos ^2 \theta\right)\right.} \\ \\ &=\dfrac{\sin \theta\left(-\sin ^2 \theta+\cos ^2 \theta\right)}{\cos \theta\left(2 \cos ^2 \theta-\sin ^2 \theta-\cos ^2 \theta\right)} \\ \\ &\because \sin ^2 \theta+\cos ^2 \theta=1 , \sin ^2 \theta-2 \sin ^2 \theta = -\sin ^2 \theta, 2 \cos ^2 \theta-\cos ^2 \theta =\cos ^2 \theta\\ \\ &=\dfrac{\sin \theta\left(\cos ^2 \theta-\sin ^2 \theta\right)}{\cos \theta\left(\cos ^2 \theta-\sin ^2 \theta\right)} \end{aligned}$
$\begin{aligned} =\frac{\sin \theta}{\cos \theta}=\tan \theta \end{aligned}$ = RHS Hence proved
(viii)
By LHS
$\begin{aligned} & =\sin ^2 A+\operatorname{cosec}^2 A+2 \sin A \operatorname{cosec} A+\cos ^2 A+\sec ^2 A+2 \cos A \sec A \\ \\ & \because (a+b)^2=a^2+b^2+2 a b \\ & \sec ^2 A=1+\tan ^2 \theta \\ & \operatorname{cosec}^2 A=1+\cot ^2 A \\ \\ & =\sin ^2 A+\cos ^2 A+\operatorname{cosec}^2 A+\sec ^2 A+2 \sin A \operatorname{cosec} A+2 \cos A \sec A \\ \\ & =1+1+\cot ^2+1+\tan ^2 A+2 \sin A \frac{1}{\sin A}+2 \cos A \times \frac{1}{\cos A} \\ \\ & =2+\cot ^2 A+1+\tan ^2 A+2+2 \\ \\ & =7+\cot ^2 A+\tan ^2 A \end{aligned}$
= RHS Hence proved
(ix)
LHS
$\begin{aligned} & \left(\dfrac{1}{\sin A}-\dfrac{\sin A}{1}\right)\left(\dfrac{1}{\cos A}-\dfrac{\cos A}{1}\right) \\ \\ &=\left(\dfrac{1-\sin ^2 A}{\sin A}\right)\left(\dfrac{1-\cos ^2 A}{\cos A}\right) \\ \\ &=\left(\dfrac{\cos ^2 A}{\sin A}\right)\left(\dfrac{\sin ^2 A}{\cos A}\right) \\ \\ &= \dfrac{\cos A \cos A}{\sin A} \times \dfrac{\sin A \sin A}{\cos A} \\ \\ &=\cos A \sin A &\end{aligned}$
RHS
$\begin{aligned} & =\dfrac{1}{\dfrac{\sin A}{\cos A}+\dfrac{\cos A}{\sin A}} \\ \\ & =\dfrac{1}{\dfrac{\sin ^2 A+\cos ^2 A}{\cos A \sin A}} \\ \\ & \because \sin^2 A+\cos ^2 A=1 \\ & \hspace{.6cm}\sin^2 A=1-\cos ^2 A \quad\quad \\ & =\dfrac{1}{\dfrac{1}{\cos A \sin A}} \\ \\ & =1 \times \dfrac{\cos A \sin A}{1} \\ \\ & =\cos A \sin A &\end{aligned}$
LHS = RHS Hence proved
(x)
LHS
$\begin{aligned} & =\dfrac{\sec ^2 A}{\operatorname{cosec}^2 A} \\ & =\dfrac{\dfrac{1}{\cos ^2 A}}{\dfrac{1}{\sin ^2 A}} \\ & =\dfrac{1}{\cos ^2 A} \times \dfrac{\sin ^2 A}{1} \\ & =\dfrac{\sin ^2 A}{\cos ^2 A}=\tan ^2 A \\ & =\left(\frac{1-\tan A}{\frac{1}{1}-\frac{1}{\tan A}}\right)^2 \\ & =\left[\frac{1-\tan A}{\frac{\tan A-1}{\tan A}}\right]^2 \\ & =\left[\frac{1-\tan A}{\frac{-(1-\tan A)}{\tan A}}\right]^2 \\ & =\left[(1-\tan A) \times \frac{(-\tan A)}{(1-\tan A)}\right]^2 \\ & =[-\tan A]^2 \\ & =\tan ^2 A \\ \end{aligned}$
LHS = RHS
8.5 Summary
In this chapter, you have studied the following points :
1. In a right triangle $A B C$, right-angled at $B$,
$ \begin{aligned} & \sin A=\dfrac{\text{ side opposite to angle } A}{\text{ hypotenuse }}, \cos A=\dfrac{\text{ side adjacent to angle } A}{\text{ hypotenuse }} \\ & \tan A=\dfrac{\text{ side opposite to angle } A}{\text{ side adjacent to angle } A} . \end{aligned} $
2. $\text{cosec} A=\dfrac{1}{\sin A} ; \sec A=\dfrac{1}{\cos A} ; \tan A=\dfrac{1}{\cot A}, \tan A=\dfrac{\sin A}{\cos A}$.
3. If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of the angle can be easily determined.
4. The values of trigonometric ratios for angles $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ and $90^{\circ}$.
5. The value of $\sin A$ or $\cos A$ never exceeds 1 , whereas the value of sec $A$ or $cosec A$ is always greater than or equal to 1 .
6. $\sin ^{2} A+\cos ^{2} A=1$,
$\sec ^{2} A-\tan ^{2} A=1$ for $0^{\circ} \leq A<90^{\circ}$,
$\text{cosec}^{2} A=1+\cot ^{2} A$ for $0^{\circ}<A \leq 90^{\circ}$.
संभवतः त्रिकोणमिति के अतिरिक्त गणणित की कोई ऐसी शाखा नहीं है, जो उसकी मध्य स्थिति का स्थान ले सकी।
J.F. Herbart (1890)
8.1 भूमिका
आप अपनी पिछली कक्षाओं में त्रिभुजों, विशेष रूप से समकोण त्रिभुजों के बारे में अध्ययन कर चुके हैं। आइए हम अपने आस-पास के परिवेश से कुछ ऐसे उदाहरण लें, जहाँ समकोण त्रिभुजों के बनने की कल्पना की जा सकती है। उदाहरण के लिए :
1. मान लीजिए एक स्कूल के छात्र कुतुबमीनार देखने गए हैं। अब, यदि कोई छात्र मीनार के शिखर को देख रहा हो, तो एक समकोण त्रिभुज बनने की कल्पना की जा सकती है जैसाकि आकृति 8.1 में दिखाया गया है। क्या वास्तव में मापे बिना ही छात्र मीनार की ऊँचाई ज्ञात कर सकता है?

आकृति 8.1
2. मान लीजिए एक लड़की नदी के किनारे स्थित अपने मकान की बालकनी पर बैठी हुई है और वह इस नदी के दूसरे किनारे पर स्थित पास ही के मंदिर की एक निचली सीढ़ी पर रखे गमले को देख रही है। इस स्थिति में, एक समकोण त्रिभुज बनने की कल्पना की जा सकती है जैसाकि आकृति 8.2 में दिखाया गया है, यदि आपको वह ऊँचाई ज्ञात हो, जिस पर लड़की बैठी हुई है, तो क्या आप नदी की चौड़ाई ज्ञात कर सकते हैं?

आकृति 8.2
3. मान लीजिए एक गर्म हवा वाला गुब्बारा हवा में उड़ रहा है। आसमान में उड़ने पर आकृति 8.2 इस गुब्बारे को एक लड़की देख लेती है और इस बात को बताने के लिए वह अपनी माँ के पास दौड़कर जाती है। गुब्बारे को देखने के लिए उसकी माँ तुरंत घर से बाहर निकल आती है। अब मान लीजिए कि जब पहले-पहल लड़की गुब्बारे को देखती है, तब गुब्बारा बिंदु $A$ पर था। जब माँ-बेटी दोनों ही गुब्बारे को देखने के लिए बाहर निकलकर आती हैं तब तक गुब्बारा एक अन्य बिंदु $\mathrm{B}$ तक आ चुका होता है। क्या आप जमीन के उस स्थान से, जहाँ माँ और बेटी दोनों खड़ी हैं, $\mathrm{B}$ की ऊँचाई ज्ञात कर सकते हैं?

आकृति 8.3
ऊपर बताई गई सभी स्थितियों में दूरियाँ अथवा ऊँचाईयाँ कुछ गणितीय तकनीकों को, जो त्रिकोणमिति नामक गणित की एक शाखा के अंतर्गत आते हैं, लागू करके ज्ञात किया जा सकता है। अंग्रेजी शब्द ’trigonometry’ की व्युत्पत्ति ग्रीक शब्दों ’tri’ (जिसका अर्थ है तीन), ‘gon’ (जिसका अर्थ है, भुजा) और ‘metron’ (जिसका अर्थ है माप) से हुई है। वस्तुतः त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच के संबंधों का अध्ययन किया जाता है। प्राचीन काल में त्रिकोणमिति पर किए गए कार्य का उल्लेख मिस्र और बेबीलॉन में मिलता है। प्राचीन काल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियाँ मापने में करते थे। आज भी इंजीनियरिंग और भौतिक विज्ञान में प्रयुक्त अधिकांश प्रौद्योगिकीय उन्नत विधियाँ त्रिकोणमितीय संकल्पनाओं पर आधारित हैं।
इस अध्याय में हम एक समकोण त्रिभुज की भुजाओं के कुछ अनुपातों का उसके न्यून कोणों के सापेक्ष अध्ययन करेंगे जिन्हें कोणों के त्रिकोणमितीय अनुपात कहते हैं। यहाँ हम अपनी चर्चा केवल न्यून कोणों तक ही सीमित रखेंगे। यद्यपि इन अनुपातों का विस्तार दूसरे कोणों के लिए भी किया जा सकता है। यहाँ हम $0^{\circ}$ और $90^{\circ}$ के माप वाले कोणों के त्रिकोणमितीय अनुपातों को भी परिभाषित करेंगे। हम कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात परिकलित करेंगे और इन अनुपातों से संबंधित कुछ सर्वसमिकाएँ (identities), जिन्हें त्रिकोणमितीय सर्वसमिकाएँ कहा जाता है, स्थापित करेंगे।
8.2 त्रिकोणमितीय अनुपात
अनुच्छेद 8.1 में आप विभिन्न स्थितियों में बने कुछ समकोण त्रिभुजों की कल्पना कर चुके हैं।
आइए हम एक समकोण त्रिभुज $\mathrm{ABC}$ लें, जैसाकि आकृति 8.4 में दिखाया गया है।

आकृति 8.4
यहाँ, $\angle \mathrm{CAB}$ (या संक्षेप में कोण $\mathrm{A}$ ) एक न्यून कोण है। कोण $\mathrm{A}$ के सापेक्ष भुजा $\mathrm{BC}$ की स्थिति पर ध्यान दीजिए। यह भुजा कोण $\mathrm{A}$ के सामने है। इस भुजा को हम कोण $\mathrm{A}$ की सम्मुख भुजा कहते हैं, भुजा $\mathrm{AC}$ समकोण त्रिभुज का कर्ण है और भुजा $\mathrm{AB}, \angle \mathrm{A}$ का एक भाग है। अतः इसे हम कोण $\mathrm{A}$ की संलग्न भुजा कहते हैं।
ध्यान दीजिए कि कोण $\mathrm{A}$ के स्थान पर कोण $\mathrm{C}$ लेने पर भुजाओं की स्थिति बदल जाती है। (देखिए आकृति 8.5)

आकृति 8.5
पिछली कक्षाओं में आप “अनुपात” की संकल्पना के बारे में अध्ययन कर चुके हैं। यहाँ अब हम समकोण त्रिभुज की भुजाओं से संबंधित कुछ अनुपातों को, जिन्हें हम त्रिकोणमितीय अनुपात कहते हैं, परिभाषित करेंगे।
समकोण त्रिभुज $\mathrm{ABC}$ (देखिए आकृति 8.4) के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपात निम्न प्रकार से परिभाषित किए जाते हैं:
$$ \begin{aligned} & \angle \mathrm{A} \text { का sine }=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कर्ण }}=\frac{\mathrm{BC}}{\mathrm{AC}} \\ & \angle \mathrm{A} \text { का cosine }=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कर्ण }}=\frac{\mathrm{AB}}{\mathrm{AC}} \end{aligned} $$
$$\angle \mathrm{A}$ का tangent $=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}=\frac{\mathrm{BC}}{\mathrm{AB}}$$
$$\angle \mathrm{A}$ का cosecant $=\frac{1}{\angle \mathrm{A} \text { का sine }}=\frac{\text { कर्ण }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AC}}{\mathrm{BC}}$$
$$\angle \mathrm{A}$ का secant $=\frac{1}{\angle \mathrm{A} \text { का cosine }}=\frac{\text { कर्ण }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AC}}{\mathrm{AB}}$$
$$\angle \mathrm{A}$ का cotangent $=\frac{1}{\angle \mathrm{A} \text { का tangent }}=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}=\frac{\mathrm{AB}}{\mathrm{BC}}$$
ऊपर परिभाषित किए गए अनुपातों को संक्षेप में क्रमशः $\sin \mathrm{A}, \cos \mathrm{A}, \tan \mathrm{A}, \operatorname{cosec} \mathrm{A}$, $\sec \mathrm{A}$ और $\cot \mathrm{A}$ लिखा जाता है। ध्यान दीजिए कि अनुपात $\operatorname{cosec} \mathrm{A}, \sec \mathrm{A}$ और $\cot \mathrm{A}$ अनुपातों $\sin \mathrm{A}, \cos \mathrm{A}$ और $\tan \mathrm{A}$ के क्रमशः व्युत्क्रम होते हैं।
और आप यहाँ यह भी देख सकते हैं कि $\tan A=\frac{B C}{A B}=\frac{\frac{B C}{A C}}{\frac{A B}{A C}}=\frac{\sin A}{\cos A}$ और $\cot A=\frac{\cos A}{\sin A}$.
अतः एक समकोण त्रिभुज के एक न्यून कोण के त्रिकोणमितीय अनुपात त्रिभुज के कोण और उसकी भुजाओं की लंबाई के बीच के संबंध को व्यक्त करते हैं।
क्यों न यहाँ आप एक समकोण त्रिभुज के कोण $\mathrm{C}$ के त्रिकोणमितीय अनुपातों को परिभाषित करने का प्रयास करें (देखिए आकृति 8.5)?
शब्द “sine” का सबसे पहला प्रयोग जिस रूप में आज हम करते हैं उसका उल्लेख 500 ई. में आर्यभट्ट द्वारा लिखित पुस्तक आर्यभटीयम में मिलता है। आर्यभट्ट ने शब्द अर्ध-ज्या का प्रयोग अर्ध-जीवा के लिए किया था जिसने समय-अंतराल में ज्या या जीवा का संक्षिप्त रूप ले लिया। जब पुस्तक आर्यभटीयम का अनुवाद अरबी भाषा में किया गया, तब शब्द जीवा को यथावत रख लिया गया। शब्द जीवा को साइनस (Sinus) के रूप में अनूदित किया गया, जिसका अर्थ वक्र है, जबकि अरबी रूपांतर को लैटिन में अनूदित किया गया। इसके तुरंत बाद sine के रूप में प्रयुक्त शब्द sinus भी पूरे यूरोप में गणितीय पाठों में प्रयुक्त होने लगा। खगोलविद् के एक अंग्रेजी प्रोफ़ेसर एडमंड गुंटर (1581-1626) ने पहले-पहल संक्षिप्त संकेत ’ $\sin$ ’ का प्रयोग किया था।

आर्यभट्ट $476 - 550$ सा.यु.
शब्दों ‘cosine’ और ’tangent’ का उद्गम बहुत बाद में हुआ था। cosine फलन का उद्गम पूरक कोण के sine का अभिकलन करने को ध्यान में रखकर किया गया था। आर्यभट्ट ने इसे कोटिज्या का नाम दिया था। नाम cosinus का उद्गम एडमंड गुंटर के साथ हुआ था। 1674 में अंग्रेज गणितज्ञ सर जोनास मूरे ने पहले-पहल संक्षिप्त संकेत ‘cos’ का प्रयोग किया था।
टिप्पणी : ध्यान दीजिए कि प्रतीक $\sin \mathrm{A}^{2}$ का प्रयोग कोण $\mathrm{A}^{\prime}$ के $\sin$ के संक्षिप्त रूप में किया गया है। यहाँ $\sin \mathrm{A}, \sin$ और $\mathrm{A}$ का गुणनफल नहीं है। $\mathrm{A}$ से अलग रहकर ’ $\sin$ ’ का कोई अर्थ ही नहीं होता। इसी प्रकार $\cos \mathrm{A}$, ’ $\cos$ ’ और $\mathrm{A}$ का गुणनफल नहीं है। इस प्रकार की व्याख्या अन्य त्रिकोणमितीय अनुपातों के साथ भी की जाती है।
अब, यदि हम समकोण त्रिभुज $\mathrm{ABC}$ के कर्ण $\mathrm{AC}$ पर एक बिंदु $P$ लें या बढ़ी हुई भुजा $A C$ पर बिंदु $Q$ लें और $A B$ पर लंब $\mathrm{PM}$ डालें और बढ़ी हुई भुजा $\mathrm{AB}$ पर लंब $\mathrm{QN}$ डालें (देखिए आकृति 8.6), तो $\triangle \mathrm{PAM}$ के $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों और $\triangle \mathrm{QAN}$ के $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों में क्या अंतर होगा?

आकृति 8.6
इस प्रश्न का उत्तर ज्ञात करने के लिए आइए पहले हम इन त्रिभुजों को देखें। क्या $\triangle \mathrm{PAM}$ और $\triangle \mathrm{CAB}$ समरूप हैं? आपको याद होगा कि अध्याय 6 में आप AA समरूपता कसौटी के बारे में अध्ययन कर चुके हैं। इस कसौटी को लागू करने पर आप पाएँगे कि त्रिभुज PAM और CAB समरूप हैं। अतः समरूप त्रिभुजों के गुणधर्म के अनुसार इन त्रिभुजों की संगत भुजाएँ आनुपातिक हैं।
अत:
$ \frac{AM}{AB}=\frac{AP}{AC}=\frac{MP}{BC} $
इससे हमें यह प्राप्त होता है
$ \begin{aligned} \frac{\mathrm{MP}}{\mathrm{AP}}=\frac{\mathrm{BC}}{\mathrm{AC}}=\sin \mathrm{A} \end{aligned} $
इसी प्रकार
$ \frac{\mathrm{AM}}{\mathrm{AP}}=\frac{\mathrm{AB}}{\mathrm{AC}}=\cos \mathrm{A}, \frac{\mathrm{MP}}{\mathrm{AM}}=\frac{\mathrm{BC}}{\mathrm{AB}}=\tan \mathrm{A} \text { आदि-आदि } $
इससे यह पता चलता है कि $\triangle \mathrm{PAM}$ के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपात और $\triangle \mathrm{CAB}$ के कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपातों में कोई अंतर नहीं होता।
इसी प्रकार आप यह जाँच कर सकते हैं कि $\triangle \mathrm{QAN}$ में भी $\sin \mathrm{A}$ का मान (और अन्य त्रिकोणमितीय अनुपातों का मान) समान बना रहता है।
अपने प्रेक्षणों से अब यह स्पष्ट हो जाता है कि यदि कोण समान बना रहता हो, तो एक कोण के त्रिकोणमितीय अनुपातों के मानों में त्रिभुज की भुजाओं की लंबाइयों के साथ कोई परिवर्तन नहीं होता।
टिप्पणी: सुविधा के लिए $(\sin \mathrm{A})^{2},(\cos \mathrm{A})^{2}$, आदि के स्थान पर हम क्रमशः $\sin ^{2} \mathrm{~A}, \cos ^{2} \mathrm{~A}$ आदि लिख सकते हैं। परंतु $\operatorname{cosec} \mathrm{A}=(\sin \mathrm{A})^{-1} \neq \sin ^{-1} \mathrm{~A}$ (इसे साइन इनवर्स $\mathrm{A}$ कहा जाता है)। $\sin ^{-1} \mathrm{~A}$ का एक अलग अर्थ होता है जिस पर चर्चा हम उच्च कक्षाओं में करेंगे। इसी प्रकार की परंपराएँ अन्य त्रिकोणमितीय अनुपातों पर भी लागू होती हैं। कभी-कभी ग्रीक अक्षर $\theta$ (थीटा) का प्रयोग कोण को प्रकट करने के लिए किया जाता है।
यहाँ हमने एक न्यून कोण के छः त्रिकोणमितीय अनुपात परिभाषित किए हैं। यदि हमें कोई एक अनुपात ज्ञात हो, तो क्या हम अन्य अनुपात प्राप्त कर सकते हैं? आइए हम इस पर विचार करें।
यदि एक समकोण त्रिभुज $\mathrm{ABC}$ में $\sin \mathrm{A}=\frac{1}{3}$, तब इसका अर्थ यह है कि $\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{3}$, अर्थात् त्रिभुज $\mathrm{ABC}$ की भुजाओं $\mathrm{BC}$ और $\mathrm{AC}$ की लंबाइयाँ $1: 3$ के अनुपात में हैं (देखिए आकृति 8.7)। अतः यदि $\mathrm{BC}, k$ के बराबर हो, तो $\mathrm{AC}, 3 k$ के बराबर होगी, जहाँ $k$ एक धन संख्या है। कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात करने के लिए हमें तीसरी भुजा $\mathrm{AB}$ की लंबाई ज्ञात करनी होती है। क्या आपको पाइथागोरस प्रमेय याद है? आइए हम पाइथागोरस प्रमेय की सहायता से अपेक्षित लंबाई $\mathrm{AB}$ ज्ञात करें।

आकृति 8.7
$ \mathrm{AB}^{2}=\mathrm{AC}^{2}-\mathrm{BC}^{2}=(3 k)^{2}-(k)^{2}=8 k^{2}=(2 \sqrt{2} k)^{2} $
अत:
$ \quad\quad\quad\mathrm{AB}= \pm 2 \sqrt{2} k $
अतः हमें प्राप्त होता है $\mathrm{AB}=2 \sqrt{2} k \quad(\mathrm{AB}=-2 \sqrt{2} k$ क्यों नहीं है? $)$
अब
$ \quad\quad\quad \quad \cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{2 \sqrt{2} k}{3 k}=\frac{2 \sqrt{2}}{3} $
इसी प्रकार, आप कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात प्राप्त कर सकते हैं।
टिप्पणी: क्योंकि समकोण त्रिभुज का कर्ण, त्रिभुज की सबसे लंबी भुजा होता है, इसलिए $\sin \mathrm{A}$ या $\cos \mathrm{A}$ का मान सदा ही 1 से कम होता है (या विशेष स्थिति में 1 के बराबर होता है।)
आइए अब हम कुछ उदाहरण लें।
उदाहरण 1 : यदि $\tan \mathrm{A}=\frac{4}{3}$, तो कोण $\mathrm{A}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।
हल : आइए सबसे पहले हम एक समकोण $\triangle \mathrm{ABC}$ खींचें (देखिए आकृति 8.8)।

आकृति 8.8
अब, हम जानते हैं कि $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{4}{3}$
अतः यदि $\mathrm{BC}=4 k$, तब $\mathrm{AB}=3 k$, जहाँ $k$ धन संख्या है।
अब पाइथागोरस प्रमेय लागू करने पर हमें यह प्राप्त होता है
$ \mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}=(4 k)^{2}+(3 k)^{2}=25 k^{2} $
इसलिए
$ \mathrm{AC}=5 k $
अब हम इनकी परिभाषाओं की सहायता से सभी त्रिकोणमितीय अनुपात लिख सकते हैं।
$ \begin{matrix} \sin A=\frac{BC}{AC}=\frac{4 k}{5 k}=\frac{4}{5} \\ \cos A=\frac{AB}{AC}=\frac{3 k}{5 k}=\frac{3}{5} \end{matrix} $
अत: $\cot \mathrm{A}=\frac{1}{\tan \mathrm{A}}=\frac{3}{4}, \operatorname{cosec} \mathrm{A}=\frac{1}{\sin \mathrm{A}}=\frac{5}{4}$ और $\sec \mathrm{A}=\frac{1}{\cos \mathrm{A}}=\frac{5}{3}$
उदाहरण 2 : यदि $\angle \mathrm{B}$ और $\angle \mathrm{Q}$ ऐसे न्यूनकोण हों जिससे कि $\sin \mathrm{B}=\sin \mathrm{Q}$, तो सिद्ध कीजिए कि $\angle \mathrm{B}=\angle \mathrm{Q}$
हल : आइए हम दो समकोण त्रिभुज $\mathrm{ABC}$ और $\mathrm{PQR}$ लें, जहाँ $\sin \mathrm{B}=\sin \mathrm{Q}$ (देखिए आकृति 8.9)।

आकृति 8.9
यहाँ
$ \sin B=\frac{A C}{A B} $
$ \text{ और } \quad \quad \quad \quad \quad \sin Q=\frac{P R}{P Q} $
तब $ \quad \quad \quad \frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{PR}}{\mathrm{PQ}} $
अत :
$$ \begin{equation*} \frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=k \text { (मान लीजिए) } \tag{1} \end{equation*} $$
अब, पाइथागोरस प्रमेय लागू करने पर हमें ये प्राप्त होते हैं
$ \mathrm{BC}=\sqrt{\mathrm{AB}^{2}-\mathrm{AC}^{2}} $
और
$ \begin{aligned} QR & =\sqrt{PQ^{2}-PR^{2}} \end{aligned} $
अत: $\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\sqrt{\mathrm{AB}^{2}-\mathrm{AC}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=\frac{\sqrt{k^{2} \mathrm{PQ}^{2}-k^{2} \mathrm{PR}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=\frac{k \sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}{\sqrt{\mathrm{PQ}^{2}-\mathrm{PR}^{2}}}=k$
(1) और (2) से हमें यह प्राप्त होता है
$$ \frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}} $$
तब प्रमेय 6.4 का प्रयोग करने पर $\triangle \mathrm{ACB} \sim \triangle \mathrm{PRQ}$ प्राप्त होता है। अतः $\angle \mathrm{B}=\angle \mathrm{Q}$
उदाहरण 3 : $\triangle \mathrm{ACB}$ लीजिए जिसका कोण $\mathrm{C}$ समकोण है जिसमें $\mathrm{AB}=29$ इकाई, $\mathrm{BC}=21$ इकाई और $\angle \mathrm{ABC}=\theta$ (देखिए आकृति 8.10) हैं तो निम्नलिखित के मान ज्ञात कीजिए।

आकृति 8.10
(i) $\cos ^{2} \theta+\sin ^{2} \theta$
(ii) $\cos ^{2} \theta-\sin ^{2} \theta$.
हल : $\triangle \mathrm{ACB}$ में हमें यह प्राप्त होता है
$$ \begin{aligned} \mathrm{AC} & =\sqrt{\mathrm{AB}^{2}-\mathrm{BC}^{2}}=\sqrt{(29)^{2}-(21)^{2}} \quad \text { आकृति } 8.10 \\ & =\sqrt{(29-21)(29+21)}=\sqrt{(8)(50)}=\sqrt{400}=20 \text { इकाई } \end{aligned} $$
अतः $\quad \sin \theta=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{20}{29}, \cos \theta=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{21}{29}$.
अब , (i) $\cos ^{2} \theta+\sin ^{2} \theta=\left(\frac{20}{29}\right)^{2}+\left(\frac{21}{29}\right)^{2}=\frac{20^{2}+21^{2}}{29^{2}}=\frac{400+441}{841}=1$,
और (ii) $\cos ^{2} \theta-\sin ^{2} \theta=\left(\frac{21}{29}\right)^{2}-\left(\frac{20}{29}\right)^{2}=\frac{(21+20)(21-20)}{29^{2}}=\frac{41}{841}$
उदाहरण 4 : एक समकोण त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि $\tan \mathrm{A}=1$ तो सत्यापित कीजिए कि
$2 \sin \mathrm{A} \cos \mathrm{A}=1$
हल : $\triangle \mathrm{ABC}$ में $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}=1$ (देखिए आकृति 8.11) अर्थात्

आकृति 8.11
अर्थात्
$ \mathrm{BC}=\mathrm{AB} $
मान लीजिए $\mathrm{AB}=\mathrm{BC}=k$, जहाँ $k$ एक धन संख्या है।
अब
$$ \begin{aligned} \mathrm{AC} & =\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}} \\ & =\sqrt{(k)^{2}+(k)^{2}}=k \sqrt{2} \end{aligned} $$
अतः
$ \sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{1}{\sqrt{2}} \text { और } \cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{1}{\sqrt{2}} $
इसलिए $\quad 2 \sin \mathrm{A} \cos \mathrm{A}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right)=1$, जो कि अपेक्षित मान है।
उदाहरण 5: $ \triangle \mathrm{OPQ}$ में, जिसका कोण $\mathrm{P}$ समकोण है, $\mathrm{OP}=7 \mathrm{~cm}$ और $\mathrm{OQ}-\mathrm{PQ}=1 \mathrm{~cm}$ (देखिए आकृति 8.12), $\sin Q$ और $\cos Q$ के मान ज्ञात कीजिए।

आकृति 8.12
हल : $\triangle \mathrm{OPQ}$ से हमें यह प्राप्त है कि
$ OQ^{2}=OP^{2}+PQ^{2} $
अर्थात्
$ (1+P Q)^{2}=OP^{2}+PQ^{2} $(क्यों?)
अर्थात्
$\quad 1+\mathrm{PQ}^{2}+2 \mathrm{PQ}=\mathrm{OP}^{2}+\mathrm{PQ}^{2}$
अर्थात्
$\quad 1+2 \mathrm{PQ}=7^{2}$(क्यों?)
अर्थात्
$ \mathrm{PQ}=24 \mathrm{~cm} \text { और } \mathrm{OQ}=1+\mathrm{PQ}=25 \mathrm{~cm} $
अत :
$ \quad \sin Q=\frac{7}{25} \text { और } \cos Q=\frac{24}{25} $
प्रश्नावली 8.1
1. $\triangle \mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, $\mathrm{AB}=24 \mathrm{~cm}$ और $\mathrm{BC}=7 \mathrm{~cm}$ है। निम्नलिखित का मान ज्ञात कीजिए :
(i) $\sin \mathrm{A}, \cos \mathrm{A}$
(ii) $\sin \mathrm{C}, \cos \mathrm{C}$
Show Answer
#missing2. आकृति 8.13 में, $\tan \mathrm{P}-\cot \mathrm{R}$ का मान ज्ञात कीजिए।
आकृति 8.13
Show Answer
#missing3. यदि $\sin \mathrm{A}=\frac{3}{4}$, तो $\cos \mathrm{A}$ और $\tan \mathrm{A}$ का मान परिकलित कीजिए।
Show Answer
#missing4. यदि $15 \cot \mathrm{A}=8$ हो तो $\sin \mathrm{A}$ और $\sec \mathrm{A}$ का मान ज्ञात कीजिए।
Show Answer
#missing5. यदि $\sec \theta=\frac{13}{12}$, हो तो अन्य सभी त्रिकोणमितीय अनुपात परिकलित कीजिए।
Show Answer
#missing6. यदि $\angle \mathrm{A}$ और $\angle \mathrm{B}$ न्यून कोण हो, जहाँ $\cos \mathrm{A}=\cos \mathrm{B}$, तो दिखाइए कि $\angle \mathrm{A}=\angle \mathrm{B}$
Show Answer
#missing7. यदि $\cot \theta=\frac{7}{8}$, तो
(i) $\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}$,
(ii) $\cot ^{2} \theta$ का मान निकालिए?
Show Answer
#missing8. यदि $3 \cot \mathrm{A}=4$, तो जाँच कीजिए कि $\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}=\cos ^{2} \mathrm{~A}-\sin ^{2} \mathrm{~A}$ है या नहीं।
Show Answer
#missing9. त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि $\tan \mathrm{A}=\frac{1}{\sqrt{3}}$, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) $\sin \mathrm{A} \cos \mathrm{C}+\cos \mathrm{A} \sin \mathrm{C}$
(ii) $\cos \mathrm{A} \cos \mathrm{C}-\sin \mathrm{A} \sin \mathrm{C}$
Show Answer
#missing10. $\triangle \mathrm{PQR}$ में, जिसका कोण $\mathrm{Q}$ समकोण है, $\mathrm{PR}+\mathrm{QR}=25 \mathrm{~cm}$ और $\mathrm{PQ}=5 \mathrm{~cm}$ है। $\sin \mathrm{P}, \cos \mathrm{P}$ और $\tan \mathrm{P}$ के मान ज्ञात कीजिए।
Show Answer
#missing11. बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) $\tan \mathrm{A}$ का मान सदैव 1 से कम होता है।
(ii) कोण $\mathrm{A}$ के किसी मान के लिए $\sec \mathrm{A}=\frac{12}{5}$
(iii) $\cos \mathrm{A}$, कोण $\mathrm{A}$ के cosecant के लिए प्रयुक्त एक संक्षिप्त रूप है।
(iv) $\cot \mathrm{A}, \cot$ और $\mathrm{A}$ का गुणनफल होता है।
(v) किसी भी कोण $\theta$ के लिए $\sin \theta=\frac{4}{3}$
Show Answer
#missing8.3 कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात
ज्यामिति के अध्ययन से आप $30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के कोणों की रचना से आप अच्छी तरह से परिचित हैं। इस अनुच्छेद में हम इन कोणों और साथ ही $0^{\circ}$ वाले कोण के त्रिकोणमितीय अनुपातों के मान ज्ञात करेंगे।
$45^{\circ}$ के त्रिकोणमितीय अनुपात
$\triangle \mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है, यदि एक कोण $45^{\circ}$ का हो, तो अन्य कोण भी $45^{\circ}$ का होगा अर्थात् $\angle \mathrm{A}=\angle \mathrm{C}=45^{\circ}$ (देखिए आकृति 8.14)।

आकृति 8.14
अत:
$ \mathrm{BC}=\mathrm{AB} \quad \text { (क्यों? }) $
अब मान लीजिए $\mathrm{BC}=\mathrm{AB}=a$
तब पाइथागोरस प्रमेय के अनुसार $\mathrm{AC}^{2}=\mathrm{AB}^{2}+\mathrm{BC}^{2}=a^{2}+a^{2}=2 a^{2}$
इसलिए $\quad \mathrm{AC}=a \sqrt{2}$.
त्रिकोणमितीय अनुपातों की परिभाषाओं को लागू करने पर हमें यह प्राप्त होता है :
$$ \begin{aligned} & \sin 45^{\circ}=\frac{45^{\circ} \text { के कोण की सम्मुख भुजा }}{\text { कर्ण }}=\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}} \\ & \cos 45^{\circ}=\frac{45^{\circ} \text { के कोण की संलग्न भुजा }}{\text { कर्ण }}=\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}} \\ & \tan 45^{\circ}=\frac{45^{\circ} \text { के कोण की सम्मुख भुजा }}{45^{\circ} \text { के कोण की संलग्न भुजा }}=\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{a}{a}=1 \end{aligned} $$
और $\operatorname{cosec} 45^{\circ}=\frac{1}{\sin 45^{\circ}}=\sqrt{2}, \sec 45^{\circ}=\frac{1}{\cos 45^{\circ}}=\sqrt{2}, \cot 45^{\circ}=\frac{1}{\tan 45^{\circ}}=1$
$30^{\circ}$ और $60^{\circ}$ के त्रिकोणमितीय अनुपात
आइए, अब हम $30^{\circ}$ और $60^{\circ}$ के त्रिकोणमितीय अनुपात परिकलित करें। एक समबाहु त्रिभुज $\mathrm{ABC}$ पर विचार करें। क्योंकि समबाहु त्रिभुज का प्रत्येक कोण, $60^{\circ}$ का होता है, इसलिए $\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}=60^{\circ}$
$\mathrm{A}$ से भुजा $\mathrm{BC}$ पर लंब $\mathrm{AD}$ डालिए (देखिए आकृति 8.15)।

आकृति 8.15
$ \begin{aligned} \text{अब } \quad \quad \quad & \Delta ABD \cong \Delta ACD \quad(\text{ क्यों? }) \\ \text{इसलिए } \quad \quad \quad & BD =DC \\ \text{ और } \quad \quad \quad & \angle BAD =\angle CAD \quad(CPCT) \end{aligned} $
अब आप यह देख सकते हैं कि:
$\triangle \mathrm{ABD}$ एक समकोण त्रिभुज है जिसका कोण $\mathrm{D}$ समकोण है, और जहाँ $\angle \mathrm{BAD}=30^{\circ}$ और $\angle \mathrm{ABD}=60^{\circ}$ ( देखिए आकृति 8.15)।
जैसा कि आप जानते हैं, कि त्रिकोणमितीय अनुपातों को ज्ञात करने के लिए हमें त्रिभुज की भुजाओं की लंबाइयाँ ज्ञात करने की आवश्यकता होती है। आइए, हम यह मान लें कि $\mathrm{AB}=2 a$
तब
$ \mathrm{BD}=\frac{1}{2} \mathrm{BC}=a $
और
$ \mathrm{AD}^{2}=\mathrm{AB}^{2}-\mathrm{BD}^{2}=(2 a)^{2}-(a)^{2}=3 a^{2} $
इसलिए
$ \mathrm{AD}=a \sqrt{3} $
अब
$$ \begin{aligned} & \sin 30^{\circ}=\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{a}{2 a}=\frac{1}{2}, \cos 30^{\circ}=\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2} \\ & \tan 30^{\circ}=\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}} \end{aligned} $$
और $\quad \operatorname{cosec} 30^{\circ}=\frac{1}{\sin 30^{\circ}}=2, \sec 30^{\circ}=\frac{1}{\cos 30^{\circ}}=\frac{2}{\sqrt{3}}$
$$ \cot 30^{\circ}=\frac{1}{\tan 30^{\circ}}=\sqrt{3} $$
इसी प्रकार
$ \begin{aligned} \sin 60^{\circ}=\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2}, \cos 60^{\circ}=\frac{1}{2}, \tan 60^{\circ}=\sqrt{3}\\ \operatorname{cosec} 60^{\circ}=\frac{2}{\sqrt{3}}, \sec 60^{\circ}=2 \text{और} \cot 60^{\circ}=\frac{1}{\sqrt{3}} \end{aligned} $
$0^{\circ}$ और $90^{\circ}$ के त्रिकोणमितीय अनुपात
आइए, हम देखें कि यदि समकोण त्रिभुज $\mathrm{ABC}$ के कोण $\mathrm{A}$ को तब तक और छोटा किया जाए जब तक कि यह शून्य नहीं हो जाता है, तब इस स्थिति में कोण $\mathrm{A}$ के त्रिकोणमितीय अनुपातों पर क्या प्रभाव पड़ता है (देखिए आकृति 8.16)। जैसे-जैसे $\angle \mathrm{A}$ छोटा होता जाता है, वैसे-वैसे भुजा $\mathrm{BC}$ की लंबाई कम होती जाती है। बिंदु $\mathrm{C}$, बिंदु $\mathrm{B}$ के निकट आता जाता है और अंत में, जब $\angle \mathrm{A}, 0^{\circ}$ के काफी निकट हो जाता है तब $\mathrm{AC}$ लगभग वही हो जाता है जो कि $\mathrm{AB}$ है (देखिए आकृति 8.17)।

आकृति 8.16

आकृति 8.17
जब $\angle \mathrm{A}, 0^{\circ}$ के अत्यधिक निकट होता है तब $\mathrm{BC}, 0$ के अत्यधिक निकट आ जाता है। तब $\sin \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AC}}$ का मान 0 के अत्यधिक निकट आ जाता है। और, जब $\angle \mathrm{A}, 0^{\circ}$ के अत्यधिक निकट होता है, तब $\mathrm{AC}$ लगभग वही होता है जो कि $\mathrm{AB}$ होता है और $\cos \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{AC}}$ का मान 1 के अत्यधिक समीप होता है।
इसकी सहायता से हम उस स्थिति में $\sin \mathrm{A}$ और $\cos \mathrm{A}$ के मान परिभाषित कर सकते हैं जबकि $\mathrm{A}=0^{\circ}$, हम $\sin 0^{\circ}=0$ और $\cos 0^{\circ}=1$ परिभाषित करते हैं।
इनका प्रयोग करने पर हमें ये प्राप्त होते हैं:
$\tan 0^{\circ}=\frac{\sin 0^{\circ}}{\cos 0^{\circ}}=0, \cot 0^{\circ}=\frac{1}{\tan 0^{\circ}}$, जो कि परिभाषित नहीं है (क्यों?)
$\sec 0^{\circ}=\frac{1}{\cos 0^{\circ}}=1$ तथा $\operatorname{cosec} 0^{\circ}=\frac{1}{\sin 0^{\circ}}$, और यह भी परिभाषित नहीं है। (क्यों?)
आइए अब हम उस स्थिति में देखें कि $\angle \mathrm{A}$ के त्रिकोणमितीय अनुपातों के साथ क्या होता है जबकि $\triangle \mathrm{ABC}$ के इस कोण को तब तक बड़ा किया जाता है, जब तक कि $90^{\circ}$ का नहीं हो जाता। $\angle \mathrm{A}$ जैसे-जैसे बड़ा होता जाता है, $\angle \mathrm{C}$ वैसे-वैसे छोटा होता जाता है। अतः ऊपर वाली स्थिति की भाँति भुजा $\mathrm{AB}$ की लंबाई कम होती जाती है। बिंदु $\mathrm{A}$, बिंदु $\mathrm{B}$ के निकट होता जाता है और, अंत में जब $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट आ जाता है, तो $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट आ जाता है और भुजा $\mathrm{AC}$ भुजा $\mathrm{BC}$ के साथ लगभग संपाती हो जाती है (देखिए आकृति 8.18)।

आकृति 8.18
जब $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट होता है तो $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट हो जाता है और भुजा $\mathrm{AC}$ लगभग वही हो जाती है, जो भुजा $\mathrm{BC}$ है। अतः $\sin \mathrm{A}, 1$ के अत्यधिक निकट हो जाता है और, जब $\angle \mathrm{A}, 90^{\circ}$ के अत्यधिक निकट होता है, तब $\angle \mathrm{C}, 0^{\circ}$ के अत्यधिक निकट हो जाता है और भुजा $\mathrm{AB}$ लगभग शून्य हो जाती है। अतः $\cos \mathrm{A}, 0$ के अत्यधिक निकट हो जाता है।
अतः हम यह परिभाषित करते हैं :
$\sin 90^{\circ}=1$ और $\cos 90^{\circ}=0$
अब आप क्यों नहीं $90^{\circ}$ के अन्य त्रिकोणमितीय अनुपात ज्ञात करते हैं?
अब हम तुरंत संदर्भ के लिए एक सारणी 8.1 के रूप में $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के सभी त्रिकोणमितीय अनुपातों के मान प्रस्तुत करेंगे।
सारणी 8.1
| $\angle \mathrm{A}$ | $\mathbf{0}^{\circ}$ | $\mathbf{3 0 ^ { \circ }}$ | $\mathbf{4 5 ^ { \circ }}$ | $\mathbf{6 0}^{\circ}$ | $\mathbf{9 0}^{\circ}$ |
|---|---|---|---|---|---|
| $\sin \mathrm{A}$ | 0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | 1 |
| $\cos \mathrm{A}$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | 0 |
| $\tan \mathrm{A}$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | अपरिभाषित |
| $\operatorname{cosec} \mathrm{A}$ | अपरिभाषित | 2 | $\sqrt{2}$ | $\frac{2}{\sqrt{3}}$ | 1 |
| $\sec \mathrm{A}$ | 1 | $\frac{2}{\sqrt{3}}$ | $\sqrt{2}$ | 2 | अपरिभाषित |
| $\cot \mathrm{A}$ | अपरिभाषित | $\sqrt{3}$ | 1 | $\frac{1}{\sqrt{3}}$ | 0 |
टिप्पणी : उपर्युक्त सारणी से आप देख सकते हैं कि जैसे-जैसे $\angle \mathrm{A}$ का मान $0^{\circ}$ से $90^{\circ}$ तक बढ़ता जाता है, $\sin \mathrm{A}$ का मान 0 से बढ़कर 1 हो जाता है और $\cos \mathrm{A}$ का मान 1 से घटकर 0 हो जाता है।
आइए, अब हम कुछ उदाहरण लेकर ऊपर की सारणी में दिए गए मानों के प्रयोग को प्रदर्शित करें।
उदाहरण 6: $ \triangle \mathrm{ABC}$ में जिसका कोण $\mathrm{B}$ समकोण है, $\mathrm{AB}=5 \mathrm{~cm}$ और $\angle \mathrm{ACB}=30^{\circ}$ ( देखिए आकृति 8.19)। भुजाओं $\mathrm{BC}$ और $\mathrm{AC}$ की लंबाइयाँ ज्ञात करें।

आकृति 8.19
हल : भुजा $\mathrm{BC}$ की लंबाई ज्ञात करने के लिए हम उस त्रिकोणमितीय अनुपात को लेंगे जिसमें $\mathrm{BC}$ और दी हुई भुजा $\mathrm{AB}$ हो। क्योंकि $\mathrm{BC}$ कोण $\mathrm{C}$ की संलग्न भुजा है, और $\mathrm{AB}$ कोण $\mathrm{C}$ की सम्मुख भुजा है, इसलिए
$ \frac{\mathrm{AB}}{\mathrm{BC}}=\tan \mathrm{C} $
अर्थात्
$ \frac{5}{\mathrm{BC}}=\tan 30^{\circ}=\frac{1}{\sqrt{3}} $
जिससे
$ \mathrm{BC}=5 \sqrt{3} \mathrm{~cm} \text { प्राप्त होता है। } $
भुजा $\mathrm{AC}$ की लंबाई ज्ञात करने के लिए हम
$ \begin{aligned} & \sin 30^{\circ} =\frac{AB}{AC} \quad \quad \quad \text{(क्यों?)} \\ \text{ अर्थात् }\quad \quad \quad & \frac{1}{2} =\frac{5}{AC} \\ \text{ अर्थात् }\quad \quad \quad & AC =10 ~cm \end{aligned} $
ध्यान दीजिए कि ऊपर के उदाहरण में तीसरी भुजा की लंबाई ज्ञात करने के लिए विकल्प के रूप में हम पाइथागोरस प्रमेय को लागू कर सकते थे,
अर्थात्
$$ \mathrm{AC}=\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}=\sqrt{5^{2}+(5 \sqrt{3})^{2}} \mathrm{~cm}=10 \mathrm{~cm} $$
उदाहरण 7: $ \triangle \mathrm{PQR}$ में, जिसका कोण $\mathrm{Q}$ समकोण है (देखिए आकृति 8.20 ), $\mathrm{PQ}=3 \mathrm{~cm}$ और $\mathrm{PR}=6 \mathrm{~cm}$ है। $\angle \mathrm{QPR}$ और $\angle \mathrm{PRQ}$ ज्ञात कीजिए।

आकृति 8.20
हल : दिया हुआ है $\mathrm{PQ}=3 \mathrm{~cm}$ और $\mathrm{PR}=6 \mathrm{~cm}$
इसलिए
$ \frac{\mathrm{PQ}}{\mathrm{PR}}=\sin \mathrm{R} $
या
$ \sin \mathrm{R}=\frac{3}{6}=\frac{1}{2} $
अत:
$ \angle \mathrm{PRQ}=30^{\circ} $
और, इसलिए
$\angle \mathrm{QPR}=60^{\circ} \quad \quad (क्यों?)$
आप यहाँ यह देख सकते हैं कि यदि एक समकोण त्रिभुज की एक भुजा और कोई एक अन्य भाग (जो या तो न्यून कोण हो या कोई एक भुजा हो) ज्ञात हो, तो त्रिभुज की शेष भुजाएँ और कोण ज्ञात किए जा सकते हैं।
उदाहरण 8 : यदि $\sin (\mathrm{A}-\mathrm{B})=\frac{1}{2}, \cos (\mathrm{A}+\mathrm{B})=\frac{1}{2}, 0^{\circ}<\mathrm{A}+\mathrm{B} \leq 90^{\circ}, \mathrm{A}>\mathrm{B}$, तो $\mathrm{A}$ और $\mathrm{B}$ ज्ञात कीजिए।
हल : क्योंकि $\sin (\mathrm{A}-\mathrm{B})=\frac{1}{2}$, इसलिए, $\mathrm{A}-\mathrm{B}=30^{\circ} \quad$ (क्यों?) $\quad \quad \quad \quad (1)$
और, क्योंकि $\cos (\mathrm{A}+\mathrm{B})=\frac{1}{2}$, इसलिए, $\mathrm{A}+\mathrm{B}=60^{\circ}$ (क्यों?) $\quad \quad \quad \quad (2)$
(1) और (2) को हल करने पर हमें $\mathrm{A}=45^{\circ}$ और $\mathrm{B}=15^{\circ}$ प्राप्त होता है।
प्रश्नावली 8.2
1. निम्नलिखित के मान निकालिए :
(i) $\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}$
(ii) $2 \tan ^{2} 45^{\circ}+\cos ^{2} 30^{\circ}-\sin ^{2} 60^{\circ}$
(iii) $\frac{\cos 45^{\circ}}{\sec 30^{\circ}+\operatorname{cosec} 30^{\circ}}$
(iv) $\frac{\sin 30^{\circ}+\tan 45^{\circ}-\operatorname{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}$
(v) $\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}$
Show Answer
#missing2. सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए:
(i) $\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}=$
(A) $\sin 60^{\circ}$
(B) $\cos 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
(ii) $\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=$
(A) $\tan 90^{\circ}$
(B) 1
(C) $\sin 45^{\circ}$
(D) 0
(iii) $\sin 2 \mathrm{~A}=2 \sin \mathrm{A}$ तब सत्य होता है, जबकि $\mathrm{A}$ बराबर है:
(A) $0^{\circ}$
(B) $30^{\circ}$
(C) $45^{\circ}$
(D) $60^{\circ}$
(iv) $\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}$ बराबर है:
(A) $\cos 60^{\circ}$
(B) $\sin 60^{\circ}$
(C) $\tan 60^{\circ}$
(D) $\sin 30^{\circ}$
Show Answer
#missing3. यदि $\tan (\mathrm{A}+\mathrm{B})=\sqrt{3}$ और $\tan (\mathrm{A}-\mathrm{B})=\frac{1}{\sqrt{3}} ; 0^{\circ}<\mathrm{A}+\mathrm{B} \leq 90^{\circ} ; \mathrm{A}>\mathrm{B}$ तो $\mathrm{A}$ और $\mathrm{B}$ का मान ज्ञात कीजिए।
Show Answer
#missing4. बताइए कि निम्नलिखित में कौन-कौन सत्य हैं या असत्य हैं। कारण सहित अपने उत्तर की पुष्टि कीजिए।
(i) $\sin (\mathrm{A}+\mathrm{B})=\sin \mathrm{A}+\sin \mathrm{B}$.
(ii) $\theta$ में वृद्धि होने के साथ $\sin \theta$ के मान में भी वृद्धि होती है।
(iii) $\theta$ में वृद्धि होने के साथ $\cos \theta$ के मान में भी वृद्धि होती है।
(iv) $\theta$ के सभी मानों पर $\sin \theta=\cos \theta$
(v) $\mathrm{A}=0^{\circ}$ पर $\cot \mathrm{A}$ परिभाषित नहीं है।
Show Answer
#missing8.4 त्रिकोणमितीय सर्वसमिकाएँ
आपको याद होगा कि एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि यह संबंधित चरों के सभी मानों के लिए सत्य हो। इसी प्रकार एक कोण के त्रिकोणमितीय अनुपातों से संबंधित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है। जबकि यह संबंधित कोण (कोणों) के सभी मानों के लिए सत्य होता है।
इस भाग में, हम एक त्रिकोणमितीय सर्वसमिका सिद्ध करेंगे और इसका प्रयोग अन्य उपयोगी त्रिकोणमितीय सर्वसमिकाओं को सिद्ध करने में करेंगे।
$\triangle \mathrm{ABC}$ में, जो $\mathrm{B}$ पर समकोण है (देखिए आकृति 8.21) हमें यह प्राप्त है
$\mathrm{AB}^{2}+\mathrm{BC}^{2}=\mathrm{AC}^{2}$

आकृति 8.21
(1) के प्रत्येक पद को $\mathrm{AC}^{2}$ से भाग देने पर हमें यह प्राप्त होता है
$ \frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AC}^{2}} $
या
$ \left(\frac{\mathrm{AB}}{\mathrm{AC}}\right)^{2}+\left(\frac{\mathrm{BC}}{\mathrm{AC}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{AC}}\right)^{2} $
अर्थात्
$ (\cos A)^{2}+(\sin A)^{2}=1 $
अर्थात्
$ \cos ^{2} A+\sin ^{2} A=1 \tag{2} $
यह सभी $\mathrm{A}$ के लिए, जहाँ $0^{\circ} \leq \mathrm{A} \leq 90^{\circ}$, सत्य होता है। अतः यह एक त्रिकोणमितीय सर्वसमिका है।
आइए, अब हम (1) को $\mathrm{AB}^{2}$ से भाग दें। ऐसा करने पर हमें यह प्राप्त होता है
$ \frac{\mathrm{AB}^{2}}{\mathrm{AB}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{AB}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{AB}^{2}} $
या
$ \left(\frac{\mathrm{AB}}{\mathrm{AB}}\right)^{2}+\left(\frac{\mathrm{BC}}{\mathrm{AB}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{AB}}\right)^{2} $
$ \text{ अर्थात् } \quad 1+\tan ^{2} A=\sec ^{2} A \tag{3} $
क्या यह समीकरण, $\mathrm{A}=0^{\circ}$ के लिए सत्य है? हाँ, यह सत्य है। क्या यह $\mathrm{A}=90^{\circ}$ के लिए भी सत्य है? $\mathrm{A}=90^{\circ}$ के लिए $\tan \mathrm{A}$ और $\sec \mathrm{A}$ परिभाषित नहीं है। अतः (3), ऐसे सभी $\mathrm{A}$ के लिए सत्य होता है, जहाँ $0^{\circ} \leq \mathrm{A}<90^{\circ}$
आइए हम यह देखें कि (1) को $\mathrm{BC}^{2}$ से भाग देने पर हमें क्या प्राप्त होता है।
$ \frac{\mathrm{AB}^{2}}{\mathrm{BC}^{2}}+\frac{\mathrm{BC}^{2}}{\mathrm{BC}^{2}}=\frac{\mathrm{AC}^{2}}{\mathrm{BC}^{2}} $
$ \text{अर्थात्} \quad \quad \quad(\frac{A B}{B C})^{2}+(\frac{B C}{B C})^{2}=(\frac{A C}{B C})^{2}$
$$\text{अर्थात्} \quad \quad \quad \cot^{2} \mathbf{A}+1=cosec^{2} \mathbf{A} \tag{4}$$
ध्यान दीजिए कि $\mathrm{A}=0^{\circ}$ के लिए $\operatorname{cosec} \mathrm{A}$ और $\cot \mathrm{A}$ परिभाषित नहीं है। अतः ऐसे सभी $\mathrm{A}$ के लिए (4) सत्य होता है जहाँ $0^{\circ}<\mathrm{A} \leq 90^{\circ}$
इन सर्वसमिकाओं का प्रयोग करके हम प्रत्येक त्रिकोणमितीय अनुपात को अन्य त्रिकोणमितीय अनुपातों के पदों में व्यक्त कर सकते हैं अर्थात् यदि कोई एक अनुपात ज्ञात हो, तो हम अन्य त्रिकोणमितीय अनुपातों के मान भी ज्ञात कर सकते हैं।
आइए हम यह देखें कि इन सर्वसमिकाओं का प्रयोग करके इसे हम कैसे ज्ञात कर सकते हैं। मान लीजिए हमें $\tan \mathrm{A}=\frac{1}{\sqrt{3}}$ ज्ञात है। तब $\cot \mathrm{A}=\sqrt{3}$
क्योंकि $\sec ^{2} \mathrm{~A}=1+\tan ^{2} \mathrm{~A}=1+\frac{1}{3}=\frac{4}{3}, \sec \mathrm{A}=\frac{2}{\sqrt{3}}$, और $\cos \mathrm{A}=\frac{\sqrt{3}}{2}$
और, क्योंकि $\sin \mathrm{A}=\sqrt{1-\cos ^{2} \mathrm{~A}}=\sqrt{1-\frac{3}{4}}=\frac{1}{2}$. इसलिए $\operatorname{cosec} \mathrm{A}=2$
उदाहरण 9 : अनुपातों $\cos \mathrm{A}, \tan \mathrm{A}$ और $\sec \mathrm{A}$ को $\sin \mathrm{A}$ के पदों में व्यक्त कीजिए।
हल : क्योंकि
$\cos ^{2} \mathrm{~A}+\sin ^{2} \mathrm{~A}=1$, इसलिए
$ \cos ^{2} \mathrm{~A}=1-\sin ^{2} \mathrm{~A} \text {, अर्थात् } \cos \mathrm{A}= \pm \sqrt{1-\sin ^{2} \mathrm{~A}} $
इससे यह प्राप्त होता है
$ \cos \mathrm{A}=\sqrt{1-\sin ^{2} \mathrm{~A}} \quad \text { (क्यों?) } $
अत: $\quad \tan \mathrm{A}=\frac{\sin \mathrm{A}}{\cos \mathrm{A}}=\frac{\sin \mathrm{A}}{\sqrt{1-\sin ^{2} \mathrm{~A}}}$ और $\sec \mathrm{A}=\frac{1}{\cos \mathrm{A}}=\frac{1}{\sqrt{1-\sin ^{2} \mathrm{~A}}}$
उदाहरण 10 : सिद्ध कीजिए कि $\sec \mathrm{A}(1-\sin \mathrm{A})(\sec \mathrm{A}+\tan \mathrm{A})=1$
हल :
वाम पक्ष $=\sec A(1-\sin A)(\sec A+\tan A)=(\frac{1}{\cos A})(1-\sin A)(\frac{1}{\cos A}+\frac{\sin A}{\cos A})$
$ \begin{aligned} & =\frac{(1-\sin A)(1+\sin A)}{\cos ^{2} A}=\frac{1-\sin ^{2} A}{\cos ^{2} A} \\ & =\frac{\cos ^{2} A}{\cos ^{2} A}=1=दाँया पक्ष \end{aligned} $
उदाहरण 11: सिद्ध कीजिए कि $\frac{\cot \mathrm{A}-\cos \mathrm{A}}{\cot \mathrm{A}+\cos \mathrm{A}}=\frac{\operatorname{cosec} \mathrm{A}-1}{\operatorname{cosec} \mathrm{A}+1}$
हल : वाम पक्ष $=\frac{\cot \mathrm{A}-\cos \mathrm{A}}{\cot \mathrm{A}+\cos \mathrm{A}}=\frac{\frac{\cos \mathrm{A}}{\sin \mathrm{A}}-\cos \mathrm{A}}{\frac{\cos \mathrm{A}}{\sin \mathrm{A}}+\cos \mathrm{A}}$
$$ \frac{\cos A\left(\frac{1}{\sin A}-1\right)}{\cos A\left(\frac{1}{\sin A}+1\right)}=\frac{\left(\frac{1}{\sin A}-1\right)}{\left(\frac{1}{\sin A}+1\right)}=\frac{\operatorname{cosec} A-1}{\operatorname{cosec} A+1}=\text { दाँया पक्ष } $$
उदाहरण 12 : सर्वसमिका $\sec ^{2} \theta=1+\tan ^{2} \theta$ का प्रयोग करके सिद्ध कीजिए कि $\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{1}{\sec \theta-\tan \theta}$
हल : क्योंकि हमें $\sec \theta$ और $\tan \theta$ से संबंधित सर्वसमिका प्रयुक्त करनी है, इसलिए आइए हम सबसे पहले सर्वसमिका के वाम पक्ष के अंश और हर को $\cos \theta$ से भाग देकर वाम पक्ष को $\sec \theta$ और $\tan \theta$ के पदों में रूपांतरित करें।
$$ \begin{aligned} \text{ वाम पक्ष } & =\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{\tan \theta-1+\sec \theta}{\tan \theta+1-\sec \theta} \\ & =\frac{(\tan \theta+\sec \theta)-1}{(\tan \theta-\sec \theta)+1}=\frac{{(\tan \theta+\sec \theta)-1}(\tan \theta-\sec \theta)}{{(\tan \theta-\sec \theta)+1}(\tan \theta-\sec \theta)} \\ & =\frac{(\tan ^{2} \theta-\sec ^{2} \theta)-(\tan \theta-\sec \theta)}{{\tan \theta-\sec \theta+1}(\tan \theta-\sec \theta)} \\ & =\frac{-1-\tan \theta+\sec \theta}{(\tan \theta-\sec \theta+1)(\tan \theta-\sec \theta)} \\ & =\frac{-1}{\tan \theta-\sec \theta}=\frac{1}{\sec \theta-\tan \theta} \end{aligned} $$
जो सिद्ध की जाने वाली अपेक्षित सर्वसमिका का दाँया पक्ष है।
प्रश्नावली 8.3
1. त्रिकोणमितीय अनुपातों $\sin \mathrm{A}, \sec \mathrm{A}$ और $\tan \mathrm{A}$ को $\cot \mathrm{A}$ के पदों में व्यक्त कीजिए।
Show Answer
#missing2. $\angle \mathrm{A}$ के अन्य सभी त्रिकोणमितीय अनुपातों को $\sec \mathrm{A}$ के पदों में लिखिए।
Show Answer
#missing3. सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए :
(i) $9 \sec ^{2} \mathrm{~A}-9 \tan ^{2} \mathrm{~A}$ बराबर है:
(A) 1 $\quad$
(B) 9 $\quad$
(C) 8 $\quad$
(D) 0
(ii) $(1+\tan \theta+\sec \theta)(1+\cot \theta-\operatorname{cosec} \theta)$ बराबर है:
(A) 0 $\quad$
(B) 1 $\quad$
(C) 2 $\quad$
(D) -1
(iii) $(\sec \mathrm{A}+\tan \mathrm{A})(1-\sin \mathrm{A})$ बराबर है:
(A) $\sec \mathrm{A}$ $\quad$
(B) $\sin \mathrm{A}$ $\quad$
(C) $\operatorname{cosec} \mathrm{A}$ $\quad$
(D) $\cos \mathrm{A}$
(iv) $\frac{1+\tan ^{2} \mathrm{~A}}{1+\cot ^{2} \mathrm{~A}}$ बराबर है:
(A) $\sec ^{2} \mathrm{~A}$ $\quad$
(B) -1 $\quad$
(C) $\cot ^{2} \mathrm{~A}$ $\quad$
(D) $\tan ^{2} \mathrm{~A}$
Show Answer
#missing4. निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए, जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण है :
(i) $(\operatorname{cosec} \theta-\cot \theta)^{2}=\frac{1-\cos \theta}{1+\cos \theta}$
(ii) $\frac{\cos \mathrm{A}}{1+\sin \mathrm{A}}+\frac{1+\sin \mathrm{A}}{\cos \mathrm{A}}=2 \sec \mathrm{A}$
(iii) $\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \operatorname{cosec} \theta$
[संकेतः व्यंजक को $\sin \theta$ और $\cos \theta$ के पदों में लिख्ए]]
(iv) $\frac{1+\sec A}{\sec A}=\frac{\sin ^2 A}{1-\cos A}$
[संकेत: वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए।]
(v) सर्वसमिका $\operatorname{cosec}^2 \mathrm{~A}=1+\cot ^2 \mathrm{~A}$ को लागू करके $ \frac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec} A+\cot A $
(vi) $\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A$
(vii) $\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta}-\tan \theta$
(viii) $(\sin \mathrm{A}+\operatorname{cosec} \mathrm{A})^2+(\cos \mathrm{A}+\sec \mathrm{A})^2=7+\tan ^2 \mathrm{~A}+\cot ^2 \mathrm{~A}$
(ix) $(\operatorname{cosec} A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}$
[संकेत : वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए]
(x) $\left(\frac{1+\tan ^2 \mathrm{~A}}{1+\cot ^2 \mathrm{~A}}\right)=\left(\frac{1-\tan \mathrm{A}}{1-\cot \mathrm{A}}\right)^2=\tan ^2 \mathrm{~A}$
Show Answer
#missing8.5 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है:
1. समकोण त्रिभुज $\mathrm{ABC}$ में, जिसका कोण $\mathrm{B}$ समकोण है,
$$ \begin{aligned} & \sin \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कर्ण }}, \cos \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }}{\text { कर्ण }} \\ & \tan \mathrm{A}=\frac{\text { कोण } \mathrm{A} \text { की सम्मुख भुजा }}{\text { कोण } \mathrm{A} \text { की संलग्न भुजा }} \end{aligned} $$
2. $\operatorname{cosec} \mathrm{A}=\frac{1}{\sin \mathrm{A}} ; \sec \mathrm{A}=\frac{1}{\cos \mathrm{A}} ; \tan \mathrm{A}=\frac{1}{\cot \mathrm{A}}, \tan \mathrm{A}=\frac{\sin \mathrm{A}}{\cos \mathrm{A}}$
3. यदि एक न्यून कोण का एक त्रिकोणमितीय अनुपात ज्ञात हो, तो कोण के शेष त्रिकोणमितीय अनुपात सरलता से ज्ञात किए जा सकते हैं।
4. $0^{\circ}, 30^{\circ}, 45^{\circ}, 60^{\circ}$ और $90^{\circ}$ के कोणों के त्रिकोणमितीय अनुपातों के मान।
5. $\sin \mathrm{A}$ या $\cos \mathrm{A}$ का मान कभी भी 1 से अधिक नहीं होता, जबकि $\sec \mathrm{A} \operatorname{या} \operatorname{cosec} \mathrm{A}$ का मान सदैव 1 से अधिक या 1 के बराबर होता है।
6. $\sin ^{2} \mathrm{~A}+\cos ^{2} \mathrm{~A}=1$
$\sec ^{2} \mathrm{~A}-\tan ^{2} \mathrm{~A}=1$ जहाँ $0^{\circ} \leq \mathrm{A}<90^{\circ}$
$\operatorname{cosec}^{2} \mathrm{~A}=1+\cot ^{2} \mathrm{~A}$ जहाँ $0^{\circ}<\mathrm{A} \leq 90^{\circ}$





