13.1 भूमिका: तल-आकृतियाँ और ठोस आकार

इस अध्याय में, आप अब तक देखी गई आकृतियों को उनकी विमाओं के रूप में (dimensions) वर्गीकृत करेंगे।

अपने दैनिक जीवन में, हम अपने परिवेश से विभिन्न आकारों की अनेक वस्तुएँ देखते हैं, जैसे पुस्तकें, गेंदें, आइसक्रीम शंकु, इत्यादि। अधिकांशतः, इन सभी वस्तुओं में एक बात सर्वनिष्ठ (common) है, वह यह है कि इनमें से प्रत्येक की कुछ लंबाई, चौड़ाई, ऊँचाई या गहराई है।

इसी कारण, ये सभी स्थान घेरते हैं और इनकी तीन विमाएँ हैं। इसीलिए, ये त्रिविमीय आकार (three dimensional shapes) कहलाते हैं

क्या आपको पिछली कक्षाओं में देखे गए कुछ त्रिविमीय आकारों (ठोस आकारों) के बारे में याद है ?

प्रयास कीजिए

आकारों का नामों से मिलान (match) कीजिए :

आकृति 13.1

उपरोक्त में से प्रत्येक आकार जैसी कुछ वस्तुओं की पहचान करने का प्रयत्न कीजिए।

इसी प्रकार के तर्क द्वारा, हम कह सकते हैं कि एक कागज़ पर खींची जा सकने वाली आकृतियों (जिनकी केवल लंबाई और चौड़ाई होती है) को द्विविमीय (two dimensional) (या तल) कहना चाहिए। हम दो विमाओं की कुछ आकृतियों को पिछली कक्षाओं में भी देख चुके हैं। द्विविमीय आकृतियों का नामों के साथ मिलान कीजिए (आकृति 13.2):

आकृति 13.2

टिप्पणी: हम संक्षेप में, द्विविमीय को 2-D और त्रिविमीय को 3-D लिख सकते हैं।

13.2 फलक, किनारे और शीर्ष

क्या आपको पहले पढ़े हुए ठोस आकारों के फलकों, शीर्षों और किनारों के बारे में कुछ याद है ? यहाँ, एक घन के लिए, इन्हें दिखाया गया है :

आकृति 13.3

घन के 8 कोने उसके शीर्ष (vertices) हैं। घन के ढाँचे को बनाने वाले 12 रेखाखंड उसके किनारे या कोर (edges) कहलाते हैं। 6 सपाट वर्गाकार पृष्ठ, जो घन की खाल या त्वचा हैं, उसके फलक (faces) कहलाते हैं।

इन्हें कीजिए

निम्नलिखित सारणी को पूरा कीजिए :

सारणी 13.1

क्या आप देख सकते हैं कि द्विविमीय आकृतियों के रूप में त्रिविमीय आकारों के फलकों की पहचान की जा सकती है ? उदाहरणार्थ, एक बेलन के दो फलक ऐसे हैं जो वृत्त हैं, तथा दर्शाए गए पिरामिड के फलक त्रिभुज हैं।

अब हम यह देखने का प्रयत्न करेंगे कि किस प्रकार कुछ 3-D आकारों को 2-D आकृतियों (अर्थात् कागज़ पर) को चित्रीय रूप से निरूपित किया जा सकता है ।

ऐसा करने के लिए, हम त्रिविमीय वस्तुओं से निकटतम रूप से परिचित होना चाहेंगे। आइए इन वस्तुओं को उनसे बनाने का प्रयास करें, जो इनके जाल (net) कहलाते हैं।

13.3 3-D आकार बनाने के लिए जाल ( नेट )

एक गत्ते का बक्सा (box) लीजिए। इसको कुछ किनारों के अनुदिश काट कर सपाट (flat) बना लीजिए। अब आपके पास इस बक्से का जाल है। जाल 2-D में एक प्रकार का ऐसा ढाँचा (या रूपरेखा) होता है (आकृति 13.4 (i)) जिसे मोड़ने पर (आकृति 13.4 (ii))। परिणामस्वरूप एक 3-D आकार प्राप्त हो जाता है (आकृति 13.4 (iii))।

आकृति 13.4

यहाँ आपने किनारों को उपयुक्त रूप से पृथक् करके, एक जाल 3 प्राप्त किया है। क्या इसकी विपरीत प्रक्रिया संभव है ? यहाँ, एक बक्से के जाल का प्रतिरूप दिया है (आकृति 13.5)। इसका प्रतिरूप बनाकर उसका विस्तार (enlarge) कर लीजिए। फिर इसे उपयुक्त प्रकार से मोड़ कर और चिपका कर एक बक्सा बनाइए।

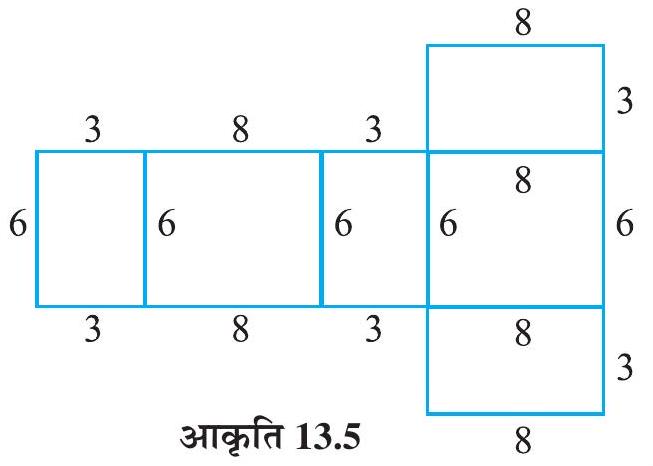
आकृति 13.5

आप उपयुक्त इकाइयों या मात्रकों (units) का प्रयोग कर सकते हैं। प्राप्त बक्सा एक ठोस है। यह घनाभ (cuboid) के आकार की एक 3-D वस्तु है। इसी प्रकार, आप एक शंकु को उसके तिर्यक पृष्ठ के अनुदिश एक पतली पट्टी (या झिरी) काट कर, इसका जाल प्राप्त कर सकते हैं (आकृति 13.6)।

आकृति 13.6

भिन्न-भिन्न आकारों के लिए, भिन्न-भिन्न जाल होते हैं। दिए हुए जालों के प्रतिरूप बनाइए और उनका विस्तार कीजिए, अथवा दिए हुए जालों के विस्तारित रूपों के प्रतिरूप बनाइए (आकृति 13.7) फिर इनके नीचे लिखें 3-D आकारों को बनाने का प्रयास कीजिए। आप गत्ते की पतली पट्टियाँ लेकर और उन्हें कागज़ के क्लिपों (clips) से बाँध कर आकारों के ढाँचे भी बनाना चाह सकते हैं।

आकृति 13.7

हम गिज़ा (मिस्न में हैं) के ग्रेट पिरामिड (Great Pyramid) (आकृति 13.8) के प्रकार के पिरामिड के लिए भी जाल बनाने का प्रयास कर सकते हैं। इस पिरामिड का आधार एक वर्ग है तथा चारों भुजाओं पर त्रिभुज बने हुए हैं। देखिए कि क्या आप दिए हुए जाल (आकृति 13.9) से इस पिरामिड को बना सकते हैं।

आकृति 13.8

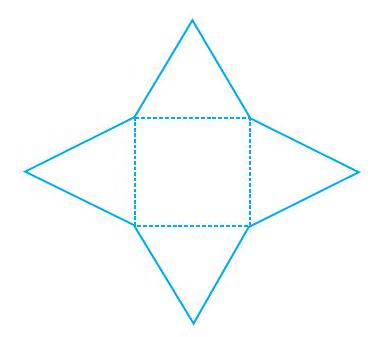
आकृति 13.9

प्रयास कीजिए

यहाँ आप चार जालों को देख रहे हैं (आकृति 13.10)। एक चतुष्फलक (tetrahedron) बनाने के लिए, इनमें से दो जाल सही हैं। देखिए कि क्या आप यह ज्ञात कर सकते हैं कि किन-किन जालों से चतुष्फलक बन सकता है।

आकृति 13.10

प्रश्नावली 13.1

1. उन जालों को पहचानिए,जिनका प्रयोग करके आप घनों को बना सकते हैं (इन जालों के प्रतिरूप काट कर ऐसा करने का प्रयास कीजिए):

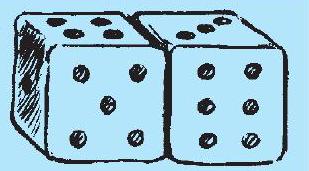
2. पासे (dice) ऐसे घन होते हैं, जिनके प्रत्येक फलक पर बिंदु (dots) अंकित होते हैं। एक पासे के सम्मुख फलकों पर अंकित बिंदुओं की संख्याओं का योग सदैव 7 होता है । यहाँ, पासे (घनों) को बनाने के लिए, दो जाल दिए जा रहे हैं। प्रत्येक वर्ग में लिखी संख्या उस बक्से के बिंदुओं को दर्शाती है ।

यह याद रखते हुए कि पासे के सम्मुख फलकों की संख्याओं का योग सदैव 7 होता है, रिक्त स्थानों पर उपयुक्त संख्याएँ लिखिए।

3. क्या यह पासे कि लिए एक जाल हो सकता है ? अपने उत्तर को स्पष्ट कीजिए।

4. यहाँ एक घन बनाने के लिए, एक अधूरा जाल दिया गया है । इसको कम-से-कम दो विभिन्न विधियों से पूरा कीजिए। याद रखिए कि घन के 6 फलक होते हैं। यहाँ इस जाल में कितने फलक दिए हुए हैं। (दो पृथक्-पृथक् चित्र दीजिए। कार्य को सरल बनाने के लिए, आप वर्गांकित कागज़ का प्रयोग कर सकते हैं।)

5. जालों को उपयुक्त ठोसों से मिलान कीजिए :

यह खेल खेलिए :

आप और आपका मित्र परस्पर पीठ-से-पीठ मिलाकर बैठे हैं। आप में से एक व्यक्ति कोई 3-D आकार बनाने के लिए एक जाल पढ़ता है, जबकि दूसरा व्यक्ति इसका प्रतिरूप बना कर, बोले गए 3-D आकार को खींचने या बनाने का प्रयत्न करता है।

13.4 एक सपाट पृष्ठ पर ठोसों को खींचना

आपका यह सपाट पृष्ठ एक कागज़ है। जब आप एक ठोस आकार को खींचते हैं, तो प्रतिबिंबों को कुछ विकृत (टेढ़ा) कर दिया जाता है, ताकि वे त्रिविमीय दिखाई दें। यह एक दृष्टिभ्रम है । यहाँ आपकी सहायता के लिए, दो तकनीकें दी जा रही हैं।

13.4.1 तिर्यक या अनियमित चित्र

यहाँ एक घन का चित्र दिया है (आकृति 13.11)। जब इसे सामने से देखा जाए तो इससे यह स्पष्ट पता चलता है कि एक घन कैसा दिखता है। आप इसके कुछ फलकों को देख नहीं पाते हैं।

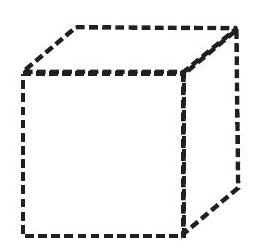
आकृति 13.11

खींचे गए इस चित्र में लंबाई बराबर नहीं है। जबकि घन में यह बराबर होनी चाहिए। फिर भी आप यह पहचान कर लेते हैं कि यह एक घन है। किसी ठोस का ऐसा चित्र एक तिर्यक (या अनियमित) चित्र (oblique sketch) कहलाता है। आप ऐसे चित्र किस प्रकार खींच सकते हैं ? आइए इसकी तकनीक को सीखने का प्रयत्न करें। आपको एक वर्गांकित (रेखांकित या बिंदुकित) कागज़ की आवश्यकता है। प्रारंभ में इस प्रकार के कागज़ पर चित्र खींचने का अभ्यास करने के बाद, आप बिना इस प्रकार के कागज़ की सहायता के सादे कागज़ पर ये चित्र सरलता से खींच सकते हैं। आइए एक $3 \times 3 \times 3$ का एक तिर्यक चित्र (एक ऐसा घन जिसका प्रत्येक किनारा 3 इकाई है) खींचने का प्रयत्न करें (आकृति 13.12)।

चरण 1

सामने का फलक खींचिए

चरण 2

सामने के फलक का सम्मुख फलक खींचिए। फलकों के माप बराबर होने चाहिए। परंतु यह चित्र चरण 1 के चित्र को कुछ खिसका कर ही बनाया गया है

चरण 3

संगत कोनों को मिलाइए

चरण 4

छिपे हुए किनारों के लिए, चित्र को बिंदुकित रेखाओं का प्रयोग करते हुए पुन: खींचिए (यह एक परंपरा या परिपाटी है) अब अभीष्ट चित्र तैयार है

आकृति 13.12

उपरोक्त तिर्यक चित्र में, क्या आप निम्नलिखित बातों को देख रहें हैं ?

(i) सामने के फलक और उसके सम्मुख फलक के माप समान हैं; तथा

(ii) घन के किनारे जो बराबर होते हैं, चित्र में भी बराबर-बराबर प्रतीत होते हैं यद्यपि इनको बराबर नहीं लिया गया है।

अब आप एक घनाभ का तिर्यक चित्र बनाने का प्रयास कर सकते हैं (याद रखिए इस स्थिति में, फलक आयत है ।

टिप्पणी : आप ऐसे चित्र भी खींच सकते हैं, जिनमें माप (या मापन), दिए हुए ठोस के मापों के अनुसार (अनुकूल) ही हो। ऐसा करने के लिए हमें एक ऐसे कागज़ की आवश्यकता होगी, जिसे समदूरीक शीट (isometric sheet) अर्थात् समान दूरियों वाली शीट) कहते हैं। आइए हम एक समदूरीक शीट पर ऐसा घनाभ बनाने का प्रयास करते हैं जिसकी लंबाई $4 \mathrm{~cm}$, चौड़ाई $3 \mathrm{~cm}$ और ऊँचाई $3 \mathrm{~cm}$ है।

13.4.2 समदूरीक चित्र

क्या आपने एक समदूरीक बिंदुकित शीट देखी है ? (इसका एक प्रतिदर्श (sample) इस पुस्तक के अंत में दिया है।) इस प्रकार की शीट में, पूरा कागज़ (अर्थात् स्वयं यह शीट) बिंदुकित रेखाओं से बने छोटे-छोटे समबाहु त्रिभुजों में बँट जाता है। ऐसे चित्र खींचने के लिए जिनके माप दिए हुए ठोस की मापों के अनुसार हों, हम इन बिंदुकित समदूरीक शीटों का प्रयोग कर सकते हैं।

आइए विमाओं $4 \times 3 \times 3$ वाले एक घनाभ (जिसका अर्थ है कि इसकी लंबाई, चौड़ाई और ऊँचाई क्रमशः 4,3 और 3 इकाइयों की हैं) का एक समदूरीक चित्र बनाने का प्रयत्न करें (आकृति 13.13)।

आकृति 13.13

ध्यान दीजिए कि एक समदूरीक चित्र में, मापन ठीक (यथार्थ में) ठोस की दी हुई मापों के होते हैं, जबकि तिर्यक चित्र की स्थिति में ऐसा नहीं होता है।

उदाहरण 1 यहाँ किसी घनाभ का एक तिर्यक चित्र दिया है (आकृति 13.14 (i))। इस चित्र से मिलान करने वाला एक समदूरीक चित्र खींचिए।

हल इसका आकृति 13.14 (ii) में चित्र खींच कर दर्शाया गया है। ध्यान दीजिए कि किस प्रकार मापों के अनुसार चित्र खींचा गया है ।

आकृति 13.14 (i)

आकृति 13.14 (ii)

आपने (i) लंबाई (ii) चौड़ाई और (iii) ऊँचाई में से प्रत्येक के अनुदिश कितनी-कितनी इकाइयाँ ली हैं ? क्या ये तिर्यक चित्र में दशाई गई इकाइयों से सुमेलित हैं?

प्रश्नावली 13.2

1. एक समदूरीक बिंदुकित कागज़ का प्रयोग करते हुए, निम्नलिखित आकृतियों में से प्रत्येक का एक समदूरीक चित्र खींचिए :

2. किसी घनाभ की विमाएँ $5 \mathrm{~cm} 3 \mathrm{~cm}$ और $2 \mathrm{~cm}$ हैं। इस घनाभ के तीन भिन्न-भिन्न समदूरीक चित्र खींचिए।

3. $2 \mathrm{~cm}$ किनारों वाले तीन घनों को परस्पर सटा कर रखते हुए एक घनाभ बनाया गया है । इस घनाभ का एक तिर्यक अथवा एक समदूरीक चित्र खींचिए।

4. निम्नलिखित समदूरीक आकारों में से प्रत्येक के लिए, एक तिर्यक चित्र खींचिए :

5. निम्नलिखित में से प्रत्येक के लिए, (i) एक तिर्यक चित्र और (ii) एक समदूरीक चित्र खींचिए :

(a) $5 \mathrm{~cm}, 3 \mathrm{~cm}$ और $2 \mathrm{~cm}$ विमाओं वाला एक घनाभ (क्या आपका चित्र अद्वितीय है ?)

(b) $4 \mathrm{~cm}$ लंबे किनारे वाला एक घन।

इस पुस्तक के अंत में, एक समदूरीक शीट लगी है। आप इस पर अपने मित्र द्वारा निर्दिष्ट विमाओं के घन या घनाभ खींच सकते हैं।

13.4.3 ठोस वस्तुओं का चित्रण

इन्हें कीजिए

कभी-कभी जब आप संयोजित या जुड़े हुए आकारों को देखते हैं, तो इनमें से कुछ आपकी दृष्टि से छिप जाते हैं, अर्थात् आपको दिखाई नहीं देते हैं।

यहाँ कुछ क्रियाकलाप दिए जा रहे हैं, जिन्हें आप अपने खाली समय में करने का प्रयास कर सकते हैं। इनसे आपको कुछ ठोस वस्तुओं के चित्रण या उनके बारे में यह कल्पना करने में सहायता मिलेगी कि वे कैसे दिखाई देते हैं।

आकृति 13.16

कुछ घन लीजिए तथा उन्हें आकृति 13.16 में दर्शाए अनुसार व्यवस्थित कीजिए। अब अपने मित्र से पूछिए कि वह इसका अनुमान लगाए कि तीर के चिह्न के अनुसार इसको देखने पर कितने घन दिखाई देते हैं ?

प्रयास कीजिए

यह अनुमान लगाने का प्रयत्न कीजिए कि निम्नलिखित व्यवस्थाओं में घनों की संख्या कितनी है (आकृति 13.17) ।

आकृति 13.17

इस प्रकार का चित्रीयकरण बहुत सहायक होता है। मान लीजिए आप ऐसे घनों को जोड़ कर एक घनाभ बनाते हैं। इस स्थिति में, आप यह अनुमान लगा सकते हैं कि उस घनाभ की लंबाई, चौड़ाई और ऊँचाई क्या होगी?

उदाहरण 2 यदि $2 \mathrm{~cm} \times 2 \mathrm{~cm} \times 2 \mathrm{~cm}$ विमाओं वाले दो घनों को परस्पर सटा कर रखा जाए, तो परिणामी घनाभ की विमाएँ क्या होंगी ?

हल जैसाकि आप देख सकते हैं (आकृति 13.18) जब घनों को सटा कर रखा जाता है, तो केवल लंबाई ही एक ऐसा मापन है जिसमें वृद्धि हुई है। यह $2+2=$ $4 \mathrm{~cm}$ हो जाती है। घनाभ की चौड़ाई $=2 \mathrm{~cm}$ है और ऊँचाई भी $=2 \mathrm{~cm}$ है।

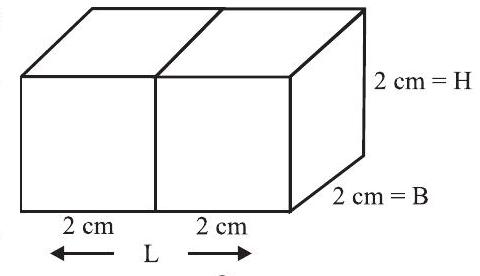
आकृति 13.18

प्रयास कीजिए

1. दो पासों को आकृति में दर्शाए अनुसार, परस्पर सटा कर रखा गया है। क्या आप बता सकते हैं कि निम्नलिखित फलकों के विपरीत फलकों पर अंकित बिंदुओं का योग क्या होगा ?

(a) $5+6$

(b) $4+3$

आकृति 13.19

(याद रखिए कि एक पासे पर सम्मुख फलकों पर अंकित संख्याओं का योग सदैव 7 होता है।)

2. $2 \mathrm{~cm}$ किनारों वाले तीन घनों को परस्पर सटा कर रखते हुए, एक घनाभ बनाया गया है। इस घनाभ का एक तिर्यक चित्र बनाने का प्रयास कीजिए और बताइए कि इसकी लंबाई, चौड़ाई और ऊँचाई क्या हो सकती है ?

13.5 किसी ठोस के विभिन्न भागों को देखना

आइए अब इस पर चर्चा करें कि एक 3-D वस्तु को किस प्रकार विभिन्न विधियों से देखा जा सकता है।

13.5.1 किसी वस्तु को देखने की एक विधि है उसे काटना या उसके पतले टुकड़े करना

टुकड़े करने वाला खेल

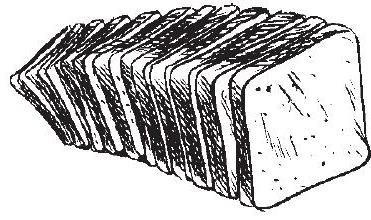
यहाँ एक डबल रोटी (bread) दी हुई है (आकृति 13.20)। यह वर्गाकार आधार वाले एक घनाभ जैसा है। आप चाकू से इसके टुकड़े कीजिए।

आकृति 13.20

जब आप इसे ऊर्ध्वाधर रूप से काटते हैं, तो आपको अनेक टुकड़े प्राप्त हो जाते हैं, जैसा आकृति 13.20 में दर्शाया गया है। एक टुकड़े का प्रत्येक फलक एक वर्ग है। हम इस फलक को डबल रोटी की एक अनुप्रस्थ-काट (cross section) कहते हैं। वस्तुतः, इस स्थिति में, अनुप्रस्थ काट लगभग एक वर्ग है। ध्यान रखिए! यदि आपका यह काटना या कटाव ‘ऊर्ध्वाधर’ नहीं होगा, तो आपको एक भिन्न अनुप्रस्थ-काट प्राप्त हो सकती है। इसके बारे में सोचिए! आपके द्वारा प्राप्त अनुप्रस्थ-काट की परिसीमा एक तल-आकृति है। क्या आप इसे देख रहे हैं?

एक रसोई खेल

क्या आपने सब्जियों के अनुप्रस्थ-काट के आकारों पर ध्यान दिया है, जब उन्हें रसोई में पकाने के लिए काटा जाता है ? विभिन्न टुकड़ों को देखिए तथा सब्जियों को काटने से प्राप्त अनुप्रस्थ-काट के आकारों से परिचित हो जाइए।

इसे खेलिए

निम्नलिखित ठोसों के मिट्टी (या प्लास्टिक की मिट्टी) के मॉडल (models) बनाइए तथा इनको ऊर्र्वाधर या क्षैतिज रूप से काटिए। अपने द्वारा प्राप्त अनुप्रस्थ-काटों के रफ़ (rough) चित्र खींजिए। जहाँ भी संभव हो, इनके नाम भी लिखिए।

आकृति 13.21

प्रश्नावली 13.3

1. आपको कौनसा अनुप्रस्थ-काट प्राप्त होती है, जब आप निम्नलिखित ठोसों को

(i) ऊर्ध्वाधर रूप से और

(ii) क्षैतिज रूप से काटते हैं ?

(a) एक ईंट

(b) एक गोल सेब

(c) एक पासा

(d) एक बेलनाकार पाइप

(e) एक आइसक्रीम शंकु

13.5.2 एक अन्य विधि छाया खेल वाली है

एक छाया खेल

यह समझाने के लिए कि किस प्रकार त्रिविमीय वस्तुओं को द्विविमीय आकारों के रूप में देखा जा सकता है, छायाएँ इनके अच्छे (या सुंदर) उदाहरण हैं।

क्या आपने कभी एक छाया खेल (shadow play) देखा है ? यह एक प्रकार का मनोरंजन है

आकृति 13.22

जिसमें सुस्पष्ट ठोस आकृतियों को एक प्रकाशमय स्रोत के सामने रखकर उनके आकृति 13.23 गतिमान प्रतिबिंबों के भ्रम उत्पन्न किए जाते हैं। इसमें गणित की अवधारणाओं का कुछ अप्रत्यक्ष रूप से प्रयोग होता है ।

आपको इस क्रियाकलाप के लिए, एक प्रकाश के स्रोत तथा कुछ ठोस आकारों की आवश्यकता होगी। (यदि आपके पास एक ओवरहैड प्रोजेक्टर (overhead projector) है, तो ठोस को बल्ब के अंतर्गत रखिए और इनकी खोज कीजिए।) एक शंकु के ठीक सामने एक टार्च का प्रकाश डालिए। यह पर्दे पर किस प्रकार की छाया दर्शाता है (आकृति 13.23)? ठोस तीन विमाओं वाला है। इसकी छाया की कितनी विमाएँ हैं ?

आकृति 13.23

यदि आप इस खेल में, शंकु के स्थान पर एक घन को टार्च के सामने रखें, तो आपको किस प्रकार की छाया प्राप्त होगी ?

प्रकाश के स्रोत की विभिन्न स्थितियों तथा ठोस वस्तु की विभिन्न स्थितियों को लेकर प्रयोग कीजिए। प्राप्त की गई छायाओं के आकारों तथा मापों पर इनके प्रभावों का अध्ययन कीजिए। यहाँ एक और मनोरंजक प्रयोग दिया जा रहा है,

जिसे संभवतः आप पहले ही कर चुके होंगे। एक वृत्ताकार चाय के प्याले को खुले में रख दीजिए, जब दोपहर 12 बजे के समय सूर्य उसके ठीक ऊपर हो। इसे आकृति 13.24 में दिखाया गया है। आपको उसकी छाया कैसी दिखाई देती है ?

क्या यह छाया एक ही प्रकार की रहती है?

सूर्य की स्थितियों और प्रेक्षण के समयों के अनुसार, छायाओं का अध्ययन कीजिए।

प्रश्नावली 13.4

1. निम्नलिखित ठोसों के ठीक ऊपर एक जलता हुआ बल्ब रखा गया है। प्रत्येक स्थिति में प्राप्त छाया के आकार का नाम बताइए। इस छाया का एक रफ़ चित्र बनाने का प्रयास कीजिए। (पहले आप प्रयोग करने का प्रयास करें और फिर उत्तर दें।)

2. यहाँ कुछ 3-D वस्तुओं की छायाएँ दी गई हैं जो उन्हें एक ओवरहैड प्रोजेक्टर के लैंप (बल्ब) के अंतर्गत या नीचे रख कर प्राप्त की गई हैं। प्रत्येक छाया से मिलान वाले ठोस की पहचान कीजिए। (इनमें एक से अधिक उत्तर हो सकते हैं!)

3. जाँच कीजिए कि क्या ये कथन सत्य हैं।

(i) एक घन एक आयत के आकार की छाया दे सकता है ।

(ii) एक घन एक षड्भुज के आकार की छाया दे सकता है।

13.5.3 एक तीसरी विधि यह है कि इसके विभिन्न दृश्य देखने के लिए इसे कुछ विशेष कोणों से देखा जाए

कोई भी व्यक्ति किसी वस्तु को उसके सामने से या उसकी एक ओर (पार्श्व) से या उसके ऊपर से देख सकता है। प्रत्येक बार उसे एक भिन्न दृश्य मिलेगा (आकृति 13.25)।

आकृति 13.25

यहाँ, एक उदाहरण दिया जा रहा है, जिसमें कोई व्यक्ति एक भवन के विभिन्न दृश्य प्राप्त कर सकता है (आकृति 13.26)।

आकृति 13.26

आप इन्हें, घनों को जोड़ने से बनी आकृतियों के लिए भी कर सकते हैं।

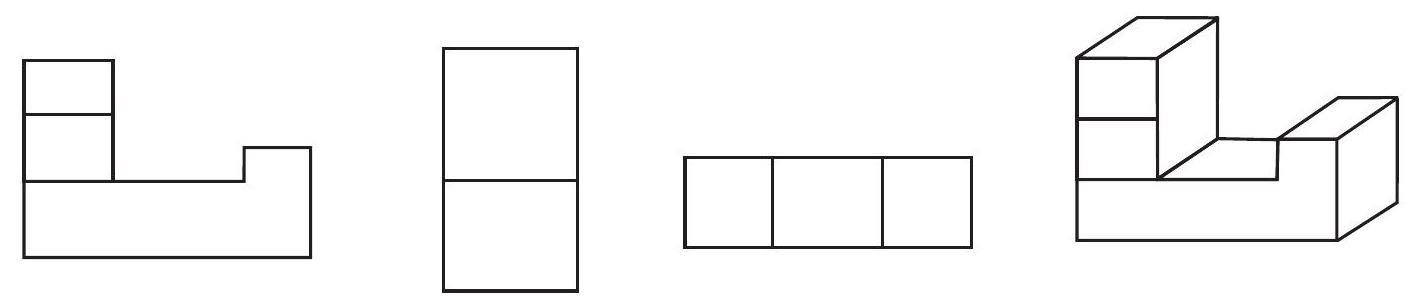
आकृति 13.27

घनों को एक साथ रखकर ठोस बनाइए और फिर उन्हें विभिन्न दिशाओं से देखकर उनके ऊपर बताए अनुसार चित्र बनाने का प्रयत्न कीजिए।

प्रयास कीजिए

1. प्रत्येक ठोस के लिए, तीन दृश्य $(1), (2)$ और $(3)$ दिए हैं। प्रत्येक ठोस के लिए संगत ऊपर के, सामने के और पाश्र्व दृश्यों की पहचान कीजिए।

2. नीचे दिए प्रत्येक ठोस का, तीर द्वारा सूचित दिशा से उसे देखने पर, एक दृश्य खींचिए।

हमने क्या चर्चा की ?

1. वृत्त, वर्ग, आयत, चतुर्भज और त्रिभुज समतल आकृतियों के उदाहरण हैं तथा घन, घनाभ, गोला, बेलन, शंकु और पिरामिड ठोस आकारों के उदाहरण हैं।

2. समतल आकृतियों की दो विमाएँ (संक्षिप्त में 2-D) होती हैं तथा ठोस आकारों की तीन विमाएँ (संक्षिप्त में 3-D) होती हैं।

3. ठोस आकार के कोने उसके शीर्ष, उसके ढाँचें के रेखाखंड उसके किनारे (या कोर) तथा उसके सपाट पृष्ठ उसके फलक कहलाते हैं।

4. ठोस का एक जाल दो विमाओं में एक ऐसा ढाँचा (या रूप रेखा) है, जिसे मोड़कर वह ठोस प्राप्त हो जाता है। एक ही ठोस के अनेक प्रकार के जाल हो सकते हैं।

5. वास्तविक रूप से, ठोस आकारों को सपाट पृष्ठों (जैसे कागज़) पर खींचा जा सकता है। हम इसे 3-D ठोस का 2-D निरूपण कहते हैं।

6. एक ठोस के दो प्रकार के चित्र बनाना संभव है :

(a) एक तिर्यक चित्र, जिसमें लंबाइयाँ समानुपाती नहीं होती हैं। फिर भी यह ठोस के रुप के बारे में सभी महत्वपूर्ण जानकारी प्रदान कर देता है।

(b) एक समदूरीक चित्र को एक समदूरीक बिंदुकित कागज़ पर खींचा जाता है, जिसका एक प्रतिदर्श इस पुस्तक के अंत में दिया गया है। किसी ठोस के एक समदूरीक चित्र में लंबाइयों को समानुपाती रखा जाता है।

7. ठोस आकारों का चित्रण एक बहुत ही उपयोगी कौशल है। आपको ठोस आकार के छिपे हुए भाग दिखाई दे जाने चाहिए।

8. एक ठोस के विभिन्न भागों को अनेक विधियों से देखा जा सकता है।

(a) एक विधि यह है कि दिए हुए आकार को काट लिया जाए। इससे हमें ठोस का एक अनुप्रस्थ-काट प्राप्त हो जाती है।

(b) एक अन्य विधि यह है कि एक 3-D आकार की एक 2-D छाया देखी जाए।

(c) तीसरी विधि यह है कि ठोस आकार को विभिन्न कोणों से देखा जाए। देखे गए आकार