9.1 भूमिका

हम अध्ययन कर चुके हैं कि किसी बंद समतल आकृति की सीमा के चारों ओर की दूरी उसका परिमाप कहलाता है और उस आकृति द्वारा घिरे हुए क्षेत्र को उसका क्षेत्रफल कहते हैं। हम त्रिभुज, आयत, वृत्त इत्यादि विभिन्न समतल आकृतियों का परिमाप और क्षेत्रफल ज्ञात करना सीख चुके हैं तथा आयताकार आकार के किनारों अथवा पगडंडियों का क्षेत्रफल भी सीख चुके हैं।

इस अध्याय में हम चतुर्भुज जैसी दूसरी बंद आकृतियों के क्षेत्रफल एवं परिमाप से संबंधित समस्याएँ हल करने का प्रयत्न करेंगे। हम घन, घनाभ और बेलन जैसे ठोसों के पृष्ठीय क्षेत्रफल एवं आयतन का भी अध्ययन करेंगे।

9.2 बहुभुज का क्षेत्रफल

हम एक चतुर्भुज को त्रिभुजों में खंडित करते हैं और इसका क्षेत्रफल ज्ञात करते हैं। इसी प्रकार की विधि बहुभुज का क्षेत्रफल ज्ञात करने के लिए उपयोग की जा सकती है। एक पंचभुज के लिए निम्नलिखित पर विचार कीजिए (आकृति 9.1, 9.2)

विकर्ण $\mathrm{AC}$ तथा $\mathrm{AD}$ की रचना करते हुए पंचभुज $\mathrm{ABCDE}$ को तीन भागों में बाँटा गया है। इसलिए $\mathrm{ABCDE}$ का क्षेत्रफल $=\triangle \mathrm{ABC}$ का क्षेत्रफल $+\triangle \mathrm{ADC}$ का क्षेत्रफल $+\triangle \mathrm{AED}$ का क्षेत्रफल।

एक विकर्ण $\mathrm{AD}$ और इस पर दो लंब $\mathrm{BF}$ एवं $\mathrm{CG}$ की रचना करते हुए पंचभुज $\mathrm{ABCDE}$ को चार भागों में बाँटा गया है। इसलिए $\mathrm{ABCDE}$ का क्षेत्रफल $=$ समकोण त्रिभुज $\mathrm{AFB}$ का क्षेत्रफल + समलंब $\mathrm{BFGC}$ का क्षेत्रफल + समकोण त्रिभुज $\mathrm{CGD}$ का क्षेत्रफल + $\triangle \mathrm{AED}$ का क्षेत्रफल (समलंब $\mathrm{BFGC}$ की समांतर भुजाओं को पहचानिए)

प्रयास कीजिए

(i) निम्नलिखित बहुभुजों (आकृति 9.3) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलंबों) में विभाजित कीजिए।

(ii) बहुभुज $\mathrm{ABCDE}$ को विभिन्न भागों में बाँटा गया है जैसा कि आकृति 9.4 में दर्शाया गया है। यदि $\mathrm{AD}=8 \mathrm{~cm}, \mathrm{AH}=6 \mathrm{~cm}, \mathrm{AG}=4 \mathrm{~cm}, \mathrm{AF}=3 \mathrm{~cm}$ और लंब $\mathrm{BF}=2 \mathrm{~cm}$, $\mathrm{CH}=3 \mathrm{~cm}, \mathrm{EG}=2.5 \mathrm{~cm}$ तो इसका क्षेत्रफल ज्ञात कीजिए। बहुभुज $\mathrm{ABCDE}$ का क्षेत्रफल $=\triangle \mathrm{AFB}$ का क्षेत्रफल $+\ldots$.

$\Delta \mathrm{AFB}$ का क्षेत्रफल $=\frac{1}{2} \times \mathrm{AF} \times \mathrm{BF}=\frac{1}{2} \times 3 \times 2=$.. समलंब $\mathrm{FBCH}$ का क्षेत्रफल $=\mathrm{FH} \times \frac{(\mathrm{BF}+\mathrm{CH})}{2}$

$$ =3 \times \frac{(2+3)}{2} \quad[\mathrm{FH}=\mathrm{AH}-\mathrm{AF}] $$

$\Delta \mathrm{CHD}$ का क्षेत्रफल $=\frac{1}{2} \times \mathrm{HD} \times \mathrm{CH}=\ldots . \Delta \mathrm{ADE}$ का क्षेत्रफल $=\frac{1}{2} \times \mathrm{AD} \times \mathrm{GE}=$ इसलिए बहुभुज $\mathrm{ABCDE}$ का क्षेत्रफल $=\ldots$.

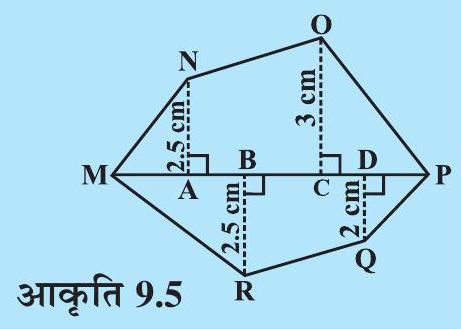
(iii) यदि $\mathrm{MP}=9 \mathrm{~cm}, \mathrm{MD}=7 \mathrm{~cm}, \mathrm{MC}=6 \mathrm{~cm}$, $\mathrm{MB}=4 \mathrm{~cm}, \mathrm{MA}=2 \mathrm{~cm}$ तो बहुभुज $\mathrm{MNOPQR}$ (आकृति 9.5) का क्षेत्रफल ज्ञात कीजिए। NA, OC, $\mathrm{QD}$ एवं $\mathrm{RB}$ विकर्ण $\mathrm{MP}$ पर खींचे गए लंब हैं।

उदाहरण 1 : समलंब के आकार के एक खेत का क्षेत्रफल $480 \mathrm{~m}^{2}$ हैं; दो समांतर भुजाओं के बीच की दूरी $15 \mathrm{~m}$ है और उनमें से एक समांतर भुजा की लंबाई $20 \mathrm{~m}$ है। दूसरी समांतर भुजा की लंबाई ज्ञात कीजिए।

हल : समलंब की समांतर भुजाओं में से एक की लंबाई $a=20 \mathrm{~m}$, मान लीजिए दूसरी समांतर भुजा $b$ है, ऊँचाई $h=15 \mathrm{~m}$

समलंब का दिया हुआ क्षेत्रफल $=480 \mathrm{~m}^{2}$

$$ \text { समलंब का क्षेत्रफल }=\frac{1}{2} h(a+b) $$

इसलिए $\quad 480=\frac{1}{2} \times 15 \times(20+b) \quad$ अथवा $\quad \frac{480 \times 2}{15}=20+b$

अथवा $64=20+b \quad$ अथवा $\quad b=44 \mathrm{~m}$

अतः समलंब की दूसरी समांतर भुजा $44 \mathrm{~m}$ है।

उदाहरण 2 : एक समचतुर्भुज का क्षेत्रफल $240 \mathrm{~cm}^{2}$ है और विकर्णों में से एक की लंबाई $16 \mathrm{~cm}$ है। दूसरा विकर्ण ज्ञात कीजिए।

हल : मान लीजिए एक विकर्ण की लंबाई $d_{1}=16 \mathrm{~cm}$

और $\qquad $ दूसरे विकर्ण की लंबाई $=d_{2}$

$\qquad \quad $ समचतुर्भुज का क्षेत्रफल $=\frac{1}{2} d_{1} \cdot d_{2}=240$

इसलिए, $\qquad \qquad \frac{1}{2} 16 \cdot d_{2}=240$

अतः, $\qquad \qquad \qquad \quad d_{2}=30 \mathrm{~cm}$

इस प्रकार दूसरे विकर्ण की लंबाई $30 \mathrm{~cm}$ है।

उदाहरण 3: MNOPQR (आकृति 9.6) एक षड्भुज है जिसकी प्रत्येक भुजा $5 \mathrm{~cm}$ है। अमन और रिधिमा ने इसे दो विभिन्न प्रकार से विभाजित किया (आकृति 9.7)। दोनों प्रकार का उपयोग करते हुए इस षड्भुज का क्षेत्रफल ज्ञात कीजिए।

हल : अमन की विधि

क्योंकि यह एक षड्भुज है इसलिए $\mathrm{NQ}$ इस षड्भुज को दो सर्वांगसम समलंबों में विभाजित करता है। आप इसे कागज़ मोड़ने की विधि से सत्यापित कर सकते हैं। (आकृति 9.8)

अब समलंब MNQR का क्षेत्रफल $=4 \times \frac{(11+5)}{2}=2 \times 16=32 \mathrm{~cm}^{2}$.

आकृति 9.9

इसलिए षड्भुज MNOPQR का क्षेत्रफल $=2 \times 32=64 \mathrm{~cm}^{2}$.

रिधिमा की विधि :

$\triangle \mathrm{MNO}$ और $\triangle \mathrm{RPQ}$ सर्वांगसम त्रिभुज हैं जिनमें से प्रत्येक का शीर्षलंब $3 \mathrm{~cm}$ है (आकृति 9.9)

आप इन त्रिभुजों को काटकर और एक-दूसरे के ऊपर रखकर इसका सत्यापन कर सकते हैं। $\triangle \mathrm{MNO}$ का क्षेत्रफल $=\frac{1}{2} \times 8 \times 3=12 \mathrm{~cm}^{2}=\triangle \mathrm{RPQ}$ का क्षेत्रफल आयत $\mathrm{MOPR}$ का क्षेत्रफल $=8 \times 5=40 \mathrm{~cm}^{2}$.

अब, षड्भुज $\mathrm{MNOPQR}$ का क्षेत्रफल $=40+12+12=64 \mathrm{~cm}^{2}$.

प्रश्नावली 9.1

1. एक मेज़ के ऊपरी पृष्ठ (सतह) का आकार समलंब जैसा है। यदि इसकी समांतर भुजाएँ $1 \mathrm{~m}$ और $1.2 \mathrm{~m}$ हैं तथा इन समांतर भुजाओं के बीच की दूरी $0.8 \mathrm{~m}$ है, तो इसका क्षेत्रफल ज्ञात कीजिए।

2. एक समलंब का क्षेत्रफल $34 \mathrm{~cm}^{2}$ है और इसकी ऊँचाई $4 \mathrm{~cm}$ है। समांतर भुजाओं में से एक की $10 \mathrm{~cm}$ लंबाई है। दूसरी समांतर भुजा की लंबाई ज्ञात कीजिए।

3. एक समलंब के आकार के खेत $\mathrm{ABCD}$ की बाड़ की लंबाई $120 \mathrm{~m}$ है। यदि $\mathrm{BC} =48 \mathrm{~m}, \mathrm{CD}=17 \mathrm{~m}$ और $\mathrm{AD}=40 \mathrm{~m}$ है, तो इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा $\mathrm{AB}$ समांतर भुजाओं $\mathrm{AD}$ तथा $\mathrm{BC}$ पर लंब है।

4. एक चतुर्भुज आकार के खेत का विकर्ण $24 \mathrm{~m}$ है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गए लंब $8 \mathrm{~m}$ एवं $13 \mathrm{~m}$ हैं। खेत का क्षेत्रफल ज्ञात कीजिए।

5. किसी समचतुर्भुज के विकर्ण $7.5 \mathrm{~cm}$ एवं $12 \mathrm{~cm}$ हैं। इसका क्षेत्रफल ज्ञात कीजिए।

6. एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा $6 \mathrm{~cm}$ और शीर्षलंब $4 \mathrm{~cm}$ है। यदि एक विकर्ण की लंबाई $8 \mathrm{~cm}$ है तो दूसरे विकर्ण की लंबाई ज्ञात कीजिए।

7. किसी भवन के फर्श में समचतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण $45 \mathrm{~cm}$ एवं $30 \mathrm{~cm}$ लंबाई के हैं। 4 रुपये प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।

8. मोहन एक समलंब के आकार का खेत खरीदना चाहता है। इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समांतर हैं और लंबाई में दुगुनी है। यदि इस खेत का क्षेत्रफल $10,500 \mathrm{~m}^{2}$ हैं और दो समांतर भुजाओं के बीच की लंबवत् दूरी $100 \mathrm{~m}$ है, तो नदी के साथ वाली भुजा की लंबाई ज्ञात कीजिए।

9. एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का है। जैसा कि आकृति में दर्शाया गया है। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कीजिए।

10. एक पंचभुज आकार का बगीचा है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया। दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?

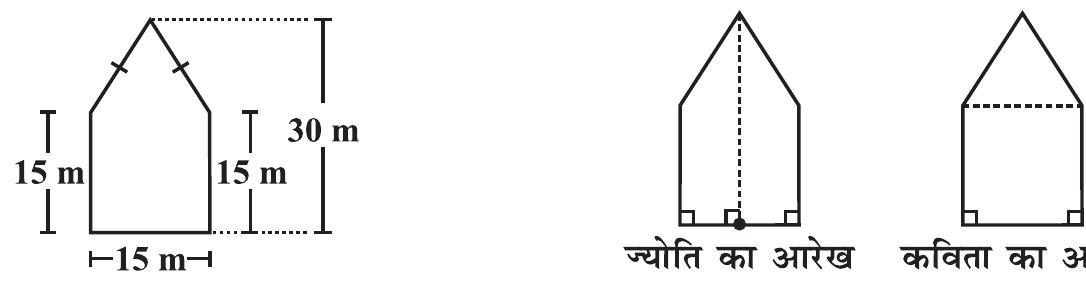
कविता का आरेख

11. संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अंतः विमाएँ क्रमशः $24 \mathrm{~cm} \times 28 \mathrm{~cm}$ एवं $16 \mathrm{~cm} \times 20 \mathrm{~cm}$ हैं। यदि फ्रेम के प्रत्येक खंड की चौड़ाई समान है, तो प्रत्येक खंड का क्षेत्रफल ज्ञात कीजिए।

9.3 ठोस आकार

आप अपनी पिछली कक्षाओं में अध्ययन कर चुके हैं कि द्विविमीय आकृतियों को त्रिविमीय आकारों के फलकों के रूप में पहचाना जा सकता है। अभी तक हमने जिन ठोसों का अध्ययन किया है उन पर ध्यान दीजिए (आकृति 9.10)।

ध्यान दीजिए कि कुछ आकारों में दो या दो से अधिक समरूप (सर्वांगसम) फलक हैं। उनको नाम दीजिए। कौन से ठोसों में सभी फलक सर्वांगसम हैं?

इन्हें कीजिए

साबुन, खिलौने, मंजन, अल्पाहार इत्यादि प्राय: घनाभकार, घनाकार अथवा बेलनाकार डिब्बों में बंद आते हैं। ऐसे डिब्बों को एकत्रित कीजिए (आकृति 9.11)।

आकृति 9.12

(यह एक लंब वृत्तीय बेलन है।)

अब एक समय में एक प्रकार के डिब्बे को लीजिए। इसके सभी फलकों को काटिए। प्रत्येक फलक के आकार को देखिए और समान फलकों को एक-दूसरे के ऊपर रखकर डिब्बे में फलकों की संख्या ज्ञात कीजिए। अपने प्रेक्षणों को लिखिए।

क्या आपने निम्नलिखित पर ध्यान दिया- बेलन के, सर्वांगसम वृत्ताकार फलक एक-दूसरे के समांतर हैं (आकृति 9.12)। ध्यान दीजिए कि वृत्ताकार फलकों के मध्य बिंदुओं को मिलाने वाला रेखाखंड आधार पर लंब है। ऐसे बेलन लंबवृत्तीय बेलन कहलाते हैं। हम केवल इस प्रकार के बेलनों का ही अध्ययन करेंगे, यद्यपि दूसरे प्रकार के बेलन भी होते हैं (आकृति 9.13)।

आकृति 9.13

(यह एक लंब वृत्तीय बेलन नहीं है।)

सोचिए, चर्चा कीजिए और लिखिए

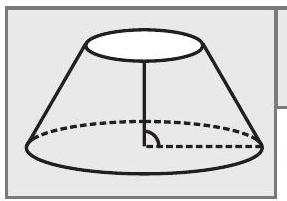
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?

9.4 घन, घनाभ और बेलन का पृष्ठीय क्षेत्रफल

इमरान, मोनिका और जसपाल क्रमशः समान ऊँचाई वाले घनाभाकार, घनाकार और बेलनाकार डिब्बों को पेंट कर रहे (आकृति 9.14)।

वे यह ज्ञात करने का प्रयास करते हैं कि किसने अधिक क्षेत्रफल को पेंट किया है। हरी उन्हें सुझाव देता है कि प्रत्येक डिब्बे का पृष्ठीय क्षेत्रफल ज्ञात करना उनकी मदद करेगा।

कुल पृष्ठीय क्षेत्रफल ज्ञात करने के लिए प्रत्येक फलक का क्षेत्रफल ज्ञात कीजिए और इनका योग कीजिए। किसी ठोस का पृष्ठीय क्षेत्रफल उसके फलकों के क्षेत्रफलों का योग होता है। और अधिक स्पष्ट करने के लिए हम प्रत्येक आकार को एक-एक करके लेते हैं।

9.4.1 घनाभ

मान लीजिए, आप एक घनाभकार डिब्बे (आकृति 9.15) को काटकर और खोलकर समतल फैला देते हैं (आकृति 9.16), हमें एक जाल (नेट) प्राप्त होता है।

प्रत्येक भुजा की विमा लिखिए। आप जानते हैं कि घनाभ में सर्वांगसम फलकों के तीन युग्म होते हैं। प्रत्येक फलक का क्षेत्रफल ज्ञात करने के लिए आप कौन-सा व्यंजक (सूत्र) उपयोग कर सकते हैं?

डिब्बे के सभी फलकों का कुल क्षेत्रफल ज्ञात कीजिए।

आकृति 9.16 हम देखते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = क्षेत्रफल $\mathrm{I}+$ क्षेत्रफल II + क्षेत्रफल III + क्षेत्रफल $\mathrm{IV}+$ क्षेत्रफल $\mathrm{V}+$ क्षेत्रफल $\mathrm{VI}$

$=h \times l+b \times l+b \times h+l \times h+b \times h+l \times b$

इसलिए कुल पृष्ठीय क्षेत्रफल $=2(h \times l+b \times h+b \times l)=2(l b+b h+h l)$

जिसमें $h, l$ और $b$ क्रमशः घनाभ की ऊँचाई, लंबाई और चौड़ाई हैं।

यदि उपर्युक्त दर्शाए गए डिब्बे की ऊँचाई, लंबाई और चौड़ाई क्रमश: $20 \mathrm{~cm}, 15 \mathrm{~cm}$ और $10 \mathrm{~cm}$ हैं, तो कुल पृष्ठीय क्षेत्रफल

$$=2(20 \times 15+20 \times 10+10 \times 15)$$

$$ =2(300+200+150)=1300 \mathrm{~m}^{2} $$

प्रयास कीजिए

निम्नलिखित घनाभों (आकृति 9.17) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

• घनाभ की दीवारें (तल एवं शीर्ष के अतिरिक्त फलक) पार्श्व पृष्ठ क्षेत्रफल प्रदान करती हैं। उदाहरणतः जिस घनाभाकार कमरे में आप बैठे हुए हैं उस कमरे की चारदीवारों का कुल क्षेत्रफल कमरे का पाश्श्व पृष्ठीय क्षेत्रफल है (आकृति 9.18)। अतः घनाभ का पाश्र्व पृष्ठीय क्षेत्रफल $2(h \times l+b \times h)$ अथवा $2 h(l+b)$ द्वारा प्राप्त किया जाता है।

इन्हें कीजिए

(i) एक घनाभाकार डस्टर (जिसे आपके अध्यापक कक्षा में उपयोग करते हैं) के पार्श्व पृष्ठ को भूरे रंग के कागज़ की पट्टी से इस प्रकार ढकिए कि यह डस्टर के पृष्ठ के चारों ओर बिल्कुल ठीक बैठे। कागज़ को हटाइए। कागज़ का क्षेत्रफल मापिए। क्या यह डस्टर का पार्श्व पृष्ठीय क्षेत्रफल है?

(ii) अपनी कक्षा के कमरे की लंबाई, चौड़ाई और ऊँचाई मापिए और निम्नलिखित को ज्ञात कीजिए :

(a) खिड़कियों और दरवाजों के क्षेत्रफल को छोड़कर कमरे का कुल पृष्ठीय क्षेत्रफल।

(b) इस कमरे का पार्श्व पृष्ठीय क्षेत्रफल।

(c) सफेदी किए जाने वाला, कमरे का कुल क्षेत्रफल।

सोचिए, चर्चा कीजिए और लिखिए

1. क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल $=$ पार्श्व पृष्ठीय क्षेत्रफल $+2 \times$ आधार का क्षेत्रफल ?

2. यदि हम किसी घनाभ (आकृति 9.19(i)) की ऊँचाई और आधार की लंबाई को परस्पर बदलकर एक दूसरा घनाभ (आकृति 9.19(ii)), प्राप्त कर लें तो क्या पाश्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?

9.4 .2 घन

इन्हें कीजिए

एक वर्गांकित कागज़ पर दर्शाए गए पैटर्न को खींचिए और उसे काटिए (आकृति 9.20(i))। आप जानते हैं कि यह पैटर्न घन का जाल (नेट) है। इसे रेखाओं के अनुदिश मोड़िए (आकृति 9.20(ii)) और घन बनाने के लिए किनारों पर टेप लगाइए (आकृति 9.20(iii))

(a) इस घन की लंबाई, चौड़ाई और ऊँचाई क्या है? ध्यान दीजिए घन के सभी फलक वर्गाकार हैं। इसलिए घन की लंबाई, चौड़ाई और ऊँचाई समान होती है (आकृति 9.21(i))।

(b) प्रत्येक फलक का क्षेत्रफल लिखिए। क्या सभी फलकों के क्षेत्रफल समान हैं?

(c) इस घन का कुल पृष्ठीय क्षेत्रफल लिखिए।

(d) यदि घन की प्रत्येक भुजा $l$ है, तो प्रत्येक फलक का क्षेत्रफल क्या होगा (आकृति 9.21(ii))। क्या हम कह सकते हैं कि $l$ भुजा वाले घन का कुल पृष्ठीय क्षेत्रफल $6 l^{2}$ है?

प्रयास कीजिए

घन $\mathrm{A}$ का पृष्ठीय क्षेत्रफल और घन $\mathrm{B}$ का पार्श्व पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति 9.22)।

सोचिए, चर्चा कीजिए और लिखिए

(i) $b$ भुजा वाले दो घनों को मिलाकर एक घनाभ बनाया गया है (आकृति 9.23)। इस घनाभ का पृष्ठीय क्षेत्रफल क्या है? क्या यह $12 b^{2}$ है? क्या ऐसे तीन घनों को मिलाकर बनाए गए घनाभ का पृष्ठीय क्षेत्रफल $18 b^{2}$ है? क्यों?

आकृति 9.23

(ii) न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?

(iii) किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति 9.24)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है? कितने घनों के 2 फलक पेंट हुए हैं? कितने घनों के तीन फलक पेंट हुए हैं?

आकृति 9.24

9.4 .3 बेलन

जितने भी बेलन हम देखते हैं उनमें से अधिकतर लंब वृत्तीय बेलन है। उदाहरणतः एक टिन, एक गोल खंभा, ट्यूबलाइट, पानी के पाइप इत्यादि :

इन्हें कीजिए

(i) एक बेलनाकार कैन अथवा डिब्बा लीजिए और इसके आधार का ग्राफ पेपर पर बनाइए और इसे काटकर बाहर निकाल लीजिए (आकृति 9.25(i))। एक ऐसा ग्राफ पेपर लीजिए जिसकी चौड़ाई कैन की ऊँचाई के समान हो। इस पट्टी को कैन के चारों ओर इस प्रकार लपेटिए ताकि यह कैन के चारों ओर बिल्कुल ठीक बैठे (अतिरिक्त कागज़ को हटा दीजिए) (आकृति 9.25(ii)) टुकड़ों को एक दूसरे से मिलाकर टेप लगाइए (आकृति 9.25(iii)) ताकि एक बेलन बन जाए (आकृति 9.25(iv)) कैन के चारों ओर लपेटे गए कागज़ का आकार क्या है।

नि:संदेह यह आकार में आयताकार है। जब आप इस बेलन के भागों को एक दूसरे से मिलाकर टेप लगा देते हैं तो आयताकार पट्टी की लंबाई वृत्त की परिधि के समान है। वृत्ताकार आधार की त्रिज्या $(r)$ और आयताकार पट्टी की लंबाई $(l)$ एवं चौड़ाई $(h)$ को नोट कीजिए। क्या $2 \pi r=$ पट्टी की लंबाई? जाँच कीजिए क्या आयताकार पट्टी का क्षेत्रफल $2 \pi r h$ है? गिनती कीजिए कि वर्गांकित कागज़ की कितनी वर्ग इकाई बेलन को निर्मित करने में उपयोग की गई है। जाँच कीजिए क्या यह गिनती $2 \pi r(r+h)$ के मान के लगभग समान है।

(ii) हम बेलन के पृष्ठीय क्षेत्रफल के रूप में संबंध $2 \pi r(r+h)$ का निगमन दूसरी विधि से भी कर सकते हैं। जैसा निम्नलिखित आकृति में दर्शाया गया है वैसे ही एक बेलन को काटने की कल्पना कीजिए (आकृति 9.26):

नोट : जब तक कुछ कहा न गया हो हम $\pi$ का मान $\frac{22}{7}$ लेते हैं।

आकृति 9.26

इसलिए बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय) क्षेत्रफल $2 \pi r h$ है।

$$ \begin{aligned} \text { बेलन का कुल पृष्ठीय क्षेत्रफल } & =\pi r^{2}+2 \pi r h+\pi r^{2} \\ & =2 \pi r^{2}+2 \pi r h \text { या } 2 \pi r(r+h) \end{aligned} $$

प्रयास कीजिए

निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति 9.27)

सोचिए, चर्चा कीजिए और लिखिए

नोट कीजिए कि किसी बेलन का पाश्श्व पृष्ठीय (वक्र पृष्ठीय क्षेत्रफल, आधार की परिधि $\times$ बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप $\times$ घनाभ की ऊँचाई के रूप में लिख सकते हैं?

उदाहरण 4 : एक मछलीघर घनाभ के आकार का है जिसके बाह्य माप $80 \mathrm{~cm} \times 30 \mathrm{~cm} \times 40 \mathrm{~cm}$ हैं। इसके तल, पृष्ठभाग वाले फलक और पीछे वाले फलक को रंगीन कागज़ से ढकना है। आवश्यक कागज़ का क्षेत्रफल ज्ञात कीजिए।

हल :

$$ \begin{aligned} \text { मछलीघर की लंबाई } & =l=80 \mathrm{~cm} \\ \text { मछलीघर की चौड़ाई } & =b=30 \mathrm{~cm} \\ \text { मछलीघर की ऊँचाई } & =h=40 \mathrm{~cm} \\ \text { आधार का क्षेत्रफल } & =l \times b=80 \times 30=2400 \mathrm{~cm}^{2} \end{aligned} $$

पृष्ठभाग वाले फलक का क्षेत्रफल $=b \times h=30 \times 40=1200 \mathrm{~cm}^{2}$

पीछे वाले फलक का क्षेत्रफल $=l \times h=80 \times 40=3200 \mathrm{~cm}^{2}$

वांछित क्षेत्रफल $=$ आधार का क्षेत्रफल + पीछे वाले फलक का क्षेत्रफल

$$ \begin{aligned} & +(2 \times \text { पृष्ठभाग वाले फलक का क्षेत्रफल }) \\ = & 2400+3200+(2 \times 1200)=8000 \mathrm{~cm}^{2} \end{aligned} $$

अतः वांछित रंगीन कागज़ का क्षेत्रफल $8000 \mathrm{~cm}^{2}$ है।

उदाहरण 5 : एक घनाभाकार कक्ष की आंतरिक माप $12 \mathrm{~m} \times 8 \mathrm{~m} \times 4 \mathrm{~m}$ है। यदि सफ़ेदी कराने का खर्च ₹ 5 प्रति वर्ग मीटर है तो उस कक्ष की चार दीवारों पर सफ़ेदी कराने का खर्च ज्ञात कीजिए। यदि उस कमरे की छत की भी सफ़ेदी कराई जाए तो सफ़ेदी कराने का खर्च कितना होगा?

हल : मान लीजिए, कमरे की लंबाई $=l=12 \mathrm{~m}$

कमरे की चौड़ाई $=b=8 \mathrm{~m}$, कमरे की ऊँचाई $=h=4 \mathrm{~m}$

कमरे की चारों दीवारों का क्षेत्रफल $=$ आधार का परिमाप $\times$ कमरे की ऊँचाई

$$ \begin{aligned} & =2(l+b) \times h=2(12+8) \times 4 \\ & =2 \times 20 \times 4=160 \mathrm{~m}^{2} \end{aligned} $$

सफ़ेदी कराने का प्रति वर्गमीटर खर्च $=$ ₹ 5

इसलिए कमरे की चार दीवारों पर सफ़ेदी कराने का कुल खर्च $=160 \times 5=$ ₹ 800

छत का क्षेत्रफल $=12 \times 8=96 \mathrm{~m}^{2}$

छत पर सफ़ेदी कराने का कुल खर्च $=96 \times 5=₹ 480$

सफ़ेदी कराने का कुल खर्च $=800+480=₹ 1280$

उदाहरण 6: एक भवन में 24 बेलनाकार खंभे हैं। प्रत्येक खंभे की त्रिज्या 28 सेमी और ऊँचाई 4 मी है। ₹ 8 प्रति वर्ग मीटर की दर से सभी खंभे के वक्र पृष्ठीय क्षेत्रफल पर पेंट कराने का व्यय ज्ञात कीजिए।

हल : बेलनाकार खंभे की त्रिज्या, $r=28 \mathrm{~cm}=0.28 \mathrm{~m}$

$\text { ऊँचाई, } h=4 \mathrm{~m}$

बेलन का वक्र पृष्ठीय क्षेत्रफल $=2 \pi r h$

खंभे का वक्र पृष्ठीय क्षेत्रफल $=2 \times \frac{22}{7} \times 0.28 \times 4=7.04 \mathrm{~m}^{2}$

ऐसे 24 खंभों का वक्र पृष्ठीय क्षेत्रफल $=7.04 \times 24=168.96 \mathrm{~m}^{2}$

$1 \mathrm{~m}^{2}$ पर पेंट कराने का खर्च $=$ ₹ 8

अतः $168.96 \mathrm{~m}^{2}$ क्षेत्रफल पर पेंट कराने का खर्च $=168.96 \times 8=$ ₹ 1351.68

उदाहरण 7 : एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए जिसकी त्रिज्या $7 \mathrm{~cm}$ और कुल पृष्ठीय क्षेत्रफल $968 \mathrm{~cm}^{2}$ है।

हल : मान लीजिए, बेलन की ऊँचाई $=h$, त्रिज्या $=r=7 \mathrm{~cm}$

$$ \begin{aligned} & \text { कुल पृष्ठीय क्षेत्रफल }=2 \pi r(h+r) \\ \text { अर्थात्} & \qquad \qquad 2 \times \frac{22}{7} \times 7 \times(7+h)=968 \quad \text { या } \quad h=15 \mathrm{~cm} \end{aligned} $$

अत: बेलन की ऊँचाई $15 \mathrm{~cm}$ है।

प्रश्नावली 9.2

1. दो घनाभाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?

2. $80 \mathrm{~cm} \times 48 \mathrm{~cm} \times 24 \mathrm{~cm}$ माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। ऐसे 100 सूटकेसों को ढकने के लिए $96 \mathrm{~cm}$ चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता है?

3. एक ऐसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल $600 \mathrm{~cm}^{2}$ है।

4. रूखसार ने $1 \mathrm{~m} \times 2 \mathrm{~m} \times 1.5 \mathrm{~m}$ माप वाली एक पेटी को बाहर से पेंट किया। यदि उसने पेटी के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया।

5. डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है जिसकी लंबाई, चौड़ाई और ऊँचाई क्रमश: $15 \mathrm{~m}, 10 \mathrm{~m}$ एवं $7 \mathrm{~m}$ हैं। पेंट की प्रत्येक कैन की सहायता से $100 \mathrm{~m}^{2}$ क्षेत्रफल को पेंट किया जा सकता है। तो उस कमरे के लिए उसे पेंट की कितनी कैनों की आवश्यकता होगी?

6. वर्णन कीजिए कि दाईं तरफ दी गई आकृतियाँ किस प्रकार एक समान हैं और किस प्रकार एक दूसरे से भिन्न हैं? किस डिब्बे का पाश्र्व पृष्ठीय क्षेत्रफल अधिक है?

7. $7 \mathrm{~m}$ त्रिज्या और $3 \mathrm{~m}$ ऊँचाई वाला एक बंद बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।

8. एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल $4224 \mathrm{~cm}^{2}$ है। इसे इसकी ऊँचाई के अनुदिश काटकर $32 \mathrm{~cm}$ चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए।

9. किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं। यदि सड़क रोलर का व्यास $84 \mathrm{~cm}$ और लंबाई $1 \mathrm{~m}$ है तो सड़क का क्षेत्रफल ज्ञात कीजिए।

10. एक कंपनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास $14 \mathrm{~cm}$ और ऊँचाई $20 \mathrm{~cm}$ है। कंपनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शाया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से $2 \mathrm{~cm}$ की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?

9.5 घन, घनाभ और बेलन का आयतन

एक त्रिविमीय वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है। अपने आसपास की वस्तुओं के आयतन की तुलना करने का प्रयत्न कीजिए। उदाहरणतः किसी कमरे के अंदर रखी हुई अलमारी की तुलना में कमरे का आयतन अधिक है। इसी प्रकार आपके पेंसिल बक्स का आयतन इसके अंदर रखे पेन और मिटाने वाली रबर के आयतन से अधिक है। क्या आप इनमें से किसी भी वस्तु का आयतन माप सकते हैं?

स्मरण कीजिए, हम किसी क्षेत्र का क्षेत्रफल ज्ञात करने के लिए वर्ग इकाई का उपयोग करते हैं। यहाँ हम ठोस का आयतन ज्ञात करने के लिए घन इकाई का उपयोग करेंगे क्योंकि घन सबसे अधिक सुविधाजनक ठोस आकार हैं (ठीक उसी प्रकार जैसे किसी क्षेत्र का क्षेत्रफल मापने के लिए वर्ग सबसे अधि क सुविधाजनक आकार है)।

क्षेत्रफल ज्ञात करने के लिए हम क्षेत्र को वर्ग इकाइयों में विभाजित करते हैं, इसी प्रकार, किसी ठोस का आयतन ज्ञात करने के लिए हमें उस ठोस को घन इकाइयों में विभाजित करने की आवश्यकता है।

विचार कीजिए कि निम्नलिखित ठोसों में से प्रत्येक का आयतन 8 घन इकाई है (आकृति 9.28)।

इस प्रकार हम कह सकते हैं कि किसी ठोस का आयतन मापने के लिए हम उसमें स्थित घन इकाइयों को गिनते हैं।

$$ \begin{align*} & 1 \text { घन सेंटीमीटर }=1 \mathrm{~cm} \times 1 \mathrm{~cm} \times 1 \mathrm{~cm}=1 \mathrm{~cm}^{3} \\ & =10 \mathrm{~mm} \times 10 \mathrm{~mm} \times 10 \mathrm{~mm}= ………………\mathrm{mm}^{3} \\ & 1 \text { घन मीटर }=1 \mathrm{~m} \times 1 \mathrm{~m} \times 1 \mathrm{~m}=1 \mathrm{~m}^{3} \\ & =……………………. \mathrm{cm}^{3}\\ & 1 \text { घन मिलीमीटर }=1 \mathrm{~mm} \times 1 \mathrm{~mm} \times 1 \mathrm{~mm}=1 \mathrm{~mm}^{3} \\ & =0.1 \mathrm{~cm} \times 0.1 \mathrm{~cm} \times 0.1 \mathrm{~cm}= ………………….\mathrm{~cm}^{3} \end{align*} $$

अब हम घनाभ, घन और बेलन का आयतन ज्ञात करने के लिए कुछ व्यंजक (सूत्र) ज्ञात करते हैं। आइए, प्रत्येक ठोस पर एक-एक करके चर्चा करते हैं।

9.5.1 घनाभ

समान आकार (प्रत्येक घन की लंबाई समान) वाले 36 घन लीजिए एक घनाभ बनाने के लिए उन्हें व्यवस्थित कीजिए। आप इन्हें अनेक रूपों में व्यवस्थित कर सकते हैं। निम्नलिखित सारणी पर विचार कीजिए और रिक्त स्थानों की पूर्ति कीजिए :

आप क्या देखते करते हैं?

क्योंकि इन घनाभों को बनाने के लिए हमने 36 घनों का उपयोग किया है इसलिए प्रत्येक घनाभ का आयतन 36 घन इकाई है। इसके अतिरिक्त प्रत्येक घनाभ का आयतन उसकी लंबाई, चौड़ाई और ऊँचाई के गुणनफल के समान है। उपर्युक्त उदाहरण से हम कह सकते हैं कि घनाभ का आयतन $=l \times b \times h$ है। क्योंकि $l \times b$ आधार का क्षेत्रफल है इसलिए हम यह भी कह सकते हैं कि घनाभ का आयतन $=$ आधार का क्षेत्रफल $\times$ ऊँचाई।

इन्हें कीजिए

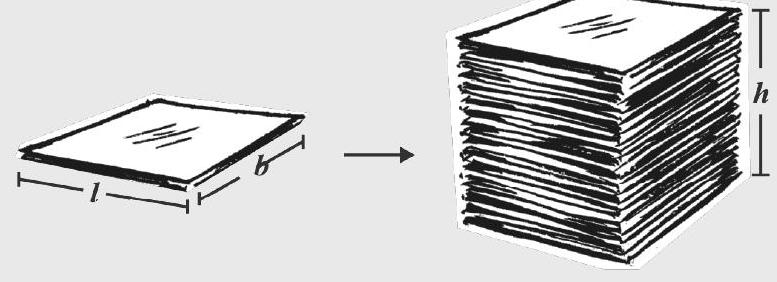
एक कागज़ की शीट लीजिए और इसके क्षेत्रफल को मापिए। इसी के समान आकार वाली कागज़ की शीटों का ढेर लगाकर एक घनाभ बनाइए (आकृति 9.29)। इस ढेर की ऊँचाई मापिए। शीट के क्षेत्रफल और शीटों की ऊँचाई का गुणनफल ज्ञात करते हुए घनाभ का आयतन ज्ञात कीजिए।

यह क्रियाकलाप इस विचार को दर्शाता है कि ठोस के आयतन का निगमन इस विधि से भी किया जा सकता है (यदि किसी ठोस का आधार और शीर्ष सर्वांगसम हैं और एक दूसरे के समांतर हैं और इसके किनारे आधार पर लंब हैं) क्या आप ऐसी वस्तुओं के बारे में सोच सकते हैं जिनका आयतन इस विधि का उपयोग करते हुए ज्ञात किया जा सकता है?

आकृति 9.29

प्रयास कीजिए

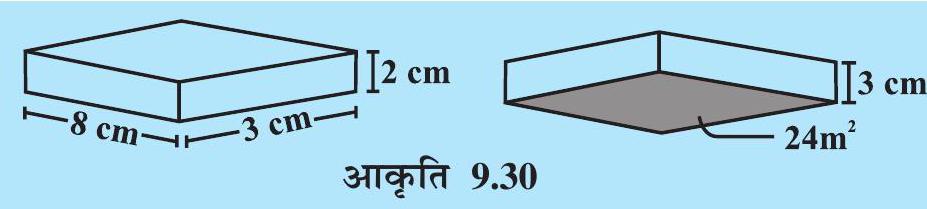
निम्नलिखित घनाभों (आकृति 9.30) का आयतन ज्ञात कीजिए :

9.5.2 घन

घन, घनाभ का एक अनोखा (विशेष) उदाहरण है जिसमें $l=b=h$. अत: घन का आयतन $=l \times l \times l=l^{3}$

प्रयास कीजिए

निम्नलिखित घनों का आयतन ज्ञात कीजिए :

(a) $4 \mathrm{~cm}$ भुजा वाला

(b) $1.5 \mathrm{~m}$ भुजा वाला

इन्हें कीजिए

समान आकार वाले 64 घनों को जितने रूपों में आप व्यवस्थित कर सकते हैं उतने रूपों में व्यवस्थित करते हुए घनाभ बनाइए। प्रत्येक रूप का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। क्या समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान होता है?

सोचिए, चर्चा कीजिए और लिखिए

एक कंपनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा $\mathrm{A} \rightarrow 3 \mathrm{~cm} \times 8 \mathrm{~cm} \times 20 \mathrm{~cm}$, डिब्बा $\mathrm{B} \rightarrow 4 \mathrm{~cm} \times 12 \mathrm{~cm} \times 10 \mathrm{~cm}$ डिब्बे का कौन सा आकार कंपनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परंतु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो।

9.5.3 बेलन

हम जानते हैं कि घनाभ का आयतन उसके आधार के क्षेत्रफल और ऊँचाई का गुणनफल ज्ञात करते हुए ज्ञात किया जा सकता है। क्या इसी प्रकार हम बेलन का आयतन ज्ञात कर सकते हैं?

घनाभ की तरह बेलन में भी एक आधार और शीर्ष होता है जो एक दूसरे के सर्वांगसम और समांतर होते हैं। घनाभ की तरह इसका वक्रपृष्ठ आधार पर लंब होता है। इसलिए

$$ \begin{aligned} \text { घनाभ का आयतन } & =\text { आधार का क्षेत्रफल } \times \text { ऊँचाई } \\ & =l \times b \times h=l b h \\ \text { बेलन का आयतन } & =\text { आधार का क्षेत्रफल } \times \text { ऊँचाई } \\ & =\pi r^{2} \times h=\pi r^{2} h \end{aligned} $$

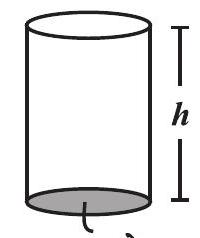
आधार का क्षेत्रफल $\left(=\pi r^{2}\right)$

9.6 आयतन और धारिता

इन दो शब्दों में अधिक अंतर नहीं है।

(a) किसी वस्तु द्वारा घिरी हुई जगह की मात्रा उसका आयतन कहलाता है।

(b) किसी बर्तन में भरी गई वस्तु की मात्रा उसकी धारिता कहलाती है।

नोट : यदि किसी पानी रखे जाने वाले टिन के बर्तन में $100 \mathrm{~cm}^{3}$ पानी भरा जा सकता है तो उस टिन के बर्तन की धारिता $100 \mathrm{~cm}^{3}$ है।

धारिता को लीटरों में भी मापा जाता है। लीटर और $\mathrm{cm}^{3}$ में निम्नलिखित संबंध है : $1 \mathrm{~mL}=1 \mathrm{~cm}^{3}, 1 \mathrm{~L}=1000 \mathrm{~cm}^{3}$. अत: $1 \mathrm{~m}^{3}$ $=1000000 \mathrm{~cm}^{3}=1000 \mathrm{~L}$.

प्रयास कीजिए

संलग्न बेलनों का आयतन ज्ञात कीजिए :

उदाहरण 8: एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए जिसका आयतन $275 \mathrm{~cm}^{3}$ और आधार का क्षेत्रफल $25 \mathrm{~cm}^{2}$ है।

हल :

घनाभ का आयतन $=$ आधार का क्षेत्रफल $\times$ ऊँचाई

अतः घनाभ की ऊँचाई $=\frac{\text { घनाभ का आयतन }}{\text { आधार का क्षेत्रफल }}=\frac{275}{25}=11 \mathrm{~cm}$

इस प्रकार घनाभ की ऊँचाई $11 \mathrm{~cm}$ है।

उदाहरण 9 : एक घनाभाकार गोदाम, जिसकी माप $60 \mathrm{~m} \times 40 \mathrm{~m} \times 30 \mathrm{~m}$ है, के अंदर कितने घनाभाकार डिब्बे रखे जा सकते हैं, यदि एक डिब्बे का आयतन 0.8 मी $^{3}$ है?

हल :

एक डिब्बे का आयतन $=0.8$ मी $^{3}$

गोदाम का आयतन $=60 \times 40 \times 30=72000$ मी $^{3}$

गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या $=\frac{\text { गोदाम का आयतन }}{1 \text { डिब्बे का आयतन }}$

$$ =\frac{60 \times 40 \times 30}{0.8}=90,000 $$

इस प्रकार गोदाम के अंदर रखे जा सकने वाले डिब्बों की संख्या 90,000 है।

उदाहरण 10: $14 \mathrm{~cm}$ चौड़ाई वाले एक आयताकार कागज़ को चौड़ाई के अनुदिश मोड़कर $20 \mathrm{~cm}$ त्रिज्या वाला एक बेलन बनाया जाता है। बेलन का आयतन ज्ञात कीजिए (आकृति 9.31)। ( $\pi$ के लिए $\frac{22}{7}$ लीजिए )

हल : कागज़ का चौड़ाई के अनुदिश मोड़कर बेलन का निर्माण किया गया है, इसलिए कागज़ की चौड़ाई बेलन की ऊँचाई होगी और बेलन की त्रिज्या $20 \mathrm{~cm}$ होगी।

$ \text { बेलन की ऊँचाई }=h=14 \mathrm{~cm} $

$ \text { त्रिज्या }=r=20 \mathrm{~cm} $

बेलन का आयतन $=\mathrm{V}=\pi r^{2} h$

$ \qquad \qquad \qquad =\frac{22}{7} \times 20 \times 20 \times 14=17600 \mathrm{~cm}^{3} $

अतः बेलन का आयतन $17600 \mathrm{~cm}^{3}$ है।

उदाहरण 11: $11 \mathrm{~cm} \times 4 \mathrm{~cm}$ माप वाले आयताकार कागज़ के टुकड़े को बिना अतिव्यापन किए, मोड़कर एक $4 \mathrm{~cm}$ ऊँचाई का बेलन बनाया जाता है। बेलन का आयतन ज्ञात कीजिए।

हल : कागज़ की लंबाई बेलन के आधार की परिधि बन जाती है और चौड़ाई, ऊँचाई बन जाती है। मान लीजिए बेलन की त्रिज्या $=r$ और ऊँचाई $=h$

$$ \text { बेलन के आधार की परिधि }=2 \pi r=11 $$

अथवा $\qquad \qquad $ $ \begin{aligned} 2 \times \frac{22}{7} \times r & =11 \ r & =\frac{7}{4} \mathrm{~cm} \end{aligned} $

इसलिए $\qquad \qquad \text { बेलन का आयतन }=\mathrm{V}=\pi r^{2} h$

$$ =\frac{22}{7} \times \frac{7}{4} \times \frac{7}{4} \times 4 \mathrm{~cm}^{3}=38.5 \mathrm{~cm}^{3} $$

अतः बेलन का आयतन $38.5 \mathrm{~cm}^{3}$ है।

प्रश्नावली 9.3

1. आपको एक बेलनाकार टैंक दिया हुआ है, निम्नलिखित में से किस स्थिति में आप उसका पृष्ठीय क्षेत्रफल ज्ञात करेंगे और किस स्थिति में आयतन :

(a) यह ज्ञात करने के लिए कि इसमें कितना पानी रखा जा सकता है।

(b) इसका प्लास्टर करने के लिए वांछित सीमेंट बोरियों की संख्या।

(c) इसमें भरे पानी से भरे जाने वाले छोटे टैंकों की संख्या।

2. बेलन $\mathrm{A}$ का व्यास $7 \mathrm{~cm}$ और ऊँचाई $14 \mathrm{~cm}$ है। बेलन $\mathrm{B}$ का व्यास $14 \mathrm{~cm}$ और ऊँचाई $7 \mathrm{~cm}$ है। परिकलन किए बिना क्या आप बता सकते हैं कि इन दोनों में किसका आयतन अधिक है। दोनों बेलनों का आयतन ज्ञात करते हुए इसका सत्यापन कीजिए। जाँच कीजिए कि क्या अधिक आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी अधिक है।

3. एक ऐसे घनाभ की ऊँचाई ज्ञात कीजिए जिसके आधार का क्षेत्रफल $180 \mathrm{~cm}^{2}$ और जिसका आयतन $900 \mathrm{~cm}^{3}$ है?

4. एक घनाभ की विमाएँ $60 \mathrm{~cm} \times 54 \mathrm{~cm} \times 30 \mathrm{~cm}$ हैं। इस घनाभ के अंदर $6 \mathrm{~cm}$ भुजा वाले कितने छोटे घन रखे जा सकते हैं।

5. एक ऐसे बेलन की ऊँचाई ज्ञात कीजिए जिसका आयतन $1.54 \mathrm{~m}^{3}$ और जिसके आधार का व्यास $140 \mathrm{~cm}$ है?

6. एक दूध का टैंक बेलन के आकार का है जिसकी त्रिज्या $1.5 \mathrm{~m}$ और लंबाई $7 \mathrm{~m}$ है। इस टैंक में भरे जा सकने वाले दूध की मात्रा लीटर में ज्ञात कीजिए।

7. यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो

(i) इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?

(ii) इसके आयतन में कितने गुना वृद्धि होगी?

8. एक कुंड के अंदर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन $108 \mathrm{~m}^{3}$ है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?

हमने क्या चर्चा की ?

1. एक ठोस का पृष्ठीय क्षेत्रफल इसके फलकों के क्षेत्रफलों के योग के समान होता है।

2. घनाभ का पृष्ठीय क्षेत्रफल $=2(l b+b h+h l)$

घन का पृष्ठीय क्षेत्रफल $=6 l^{2}$

बेलन का पृष्ठीय क्षेत्रफल $=2 \pi r(r+h)$

3. किसी ठोस द्वारा घिरी हुई जगह की मात्रा इसका आयतन कहलाती है।

4. घनाभ का आयतन $=l \times b \times h$

घन का आयतन $=l^{3}$

बेलन का आयतन $=\pi r^{2} h$

5. (i) $1 \mathrm{~cm}^{3}=1 \mathrm{~mL}$

(ii) $1 \mathrm{~L}=1000 \mathrm{~cm}^{3}$

(iii) $1 \mathrm{~m}^{3}=1000000 \mathrm{~cm}^{3}=1000 \mathrm{~L}$