title: “Lata knowledge-route-Class10-Math1-2 Merged.Pdf(1)” type: “reveal” weight: 1
| S.No. | Topics | Pages |
|---|---|---|
| 1. | Circles | $1-5$ |
| 2. | Constructions | $6-11$ |
| 3. | Heights and Distances | $12-16$ |
| 4. | Mensration | $16-28$ |
| 5. | Probability | $29-32$ |
| 6. | Quadratic Equations | $33-39$ |
| 7. | Arithmetic Progression | $40-43$ |
| 8. | Co-Ordinate Geometry | $44-52$ |
CIRCLES
9.1 CIRCLE
A circle is the locus of a points which moves in a plane in such a way that its distance from a fixed point remains constant.
9.2 SECANT AND TANGENT :
$\Rightarrow \quad$ Secant to a circle is a line which intersects the circle in two distinct points.
$\Rightarrow \quad$ A tangent to a circle is a line that intersects the circle in exactly one point.
CIRCLES
9.3 THEOREM :
Statement : A tangent to a circle i perpendicular to the radius through the point of contact.

Given : $\quad A$ circle $C(O, r)$ and a tangent $A B$ at a point $P$.
To prove : $\quad OP \perp AB$
Construction : Take any points $Q$, other than $P$ on the tangent $A B$. Join $O Q$. Suppose $O Q$ meets the circle at $R$.
CIRCLES
Proof: $\quad$ Among all line segments joining the point $O$ to a point on $A B$, the shorted one is perpendicular to $A B$. So, to prove that $O P \perp A B$, it is sufficient to prove that $O P$ is shorter than any other segment joining $O$ to any point of $A B$.
Clearly $OP = OR\quad\quad\quad$ Now, $OQ$ $OR + RQ $
$⇒ OQ > OR \quad\quad\quad$ $⇒ OQ > OP (∴OP = OR) $
Thus, $O P$ is shorter than any other segment joining $O$ to any point of $A B$.
Hence, $OP \perp AB$.
CIRCLES
9.4 THEORM :
Statement : Lengths of two tangents drawn from an external point to a circle are equal.
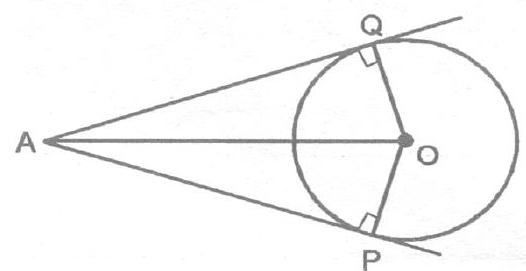
Given: $\quad A P$ and $A Q$ are two tangents drawn from a point $A$ to a circle $C(O, r)$.
To prove $A P=A Q$
Construction : Join $O P, O Q$ and $O A$.
CIRCLES
Proof : $\quad$ In $\triangle AOQ$ and $\triangle APO$
$\angle OQA=\angle OPA$ [Tangent at any point of a circle is perp. to radius through the point of contact]
$AO=AO \quad$ [Common] $OQ=OP \quad$ [Radius]
So, by R.H.S. criterion of congruency $\triangle AOQ \cong \triangle AOP$
$\therefore \quad A Q=A P$ [By CPCT] Hence Proved.
CIRCLES
Result :
(i) If two tangents are drawn to a circle from an external point, then they subtend equal angles at the centre. $\angle OAQ=\angle OAP$ [By CPCT]
(ii) If two tangents are drawn to a circle from an external point, they are equally inclined to the segment, joining the centre to that point $\angle OAQ=\angle OAP$ [By CPCT]
CIRCLES
Ex. 1 If all the sides of a parallelogram touches a circle, show that the parallelogram is a rhombus.
CIRCLES
Sol. Given : Sides $A B, B C, C D$ and $D A$ of a $|| g m$ ABCD touch a circle at $P, Q, R$ and $S$ respectively.
To prove $||^{g m} ABCD$ is a rhombus.
Proof :
$A P=A S$ …(i)
$B P=B Q$ …(ii)
$CR=CQ$ …(iii)
$DR=DS$ …(iv)

CIRCLES
[Tangents drawn from an external point to a circle are equal] Adding (1), (2), (3) and (4), we get
$\Rightarrow A P+B P+C R+D R=A S+B Q+C Q+D S $
$\Rightarrow (A P+B P)+(C R+D R)= A S+D S_+(B Q+C Q). $
$\Rightarrow A B+C D=A D+B C $
$\Rightarrow A B+A B=A D+A D \quad \quad $ ${[\text { In a } || \text { gm } A B C D, \text {opposite side are equal] }}$
$\Rightarrow 2 A B=2 A D \text { or } A B=A D $
$\text { But } A B=C D \quad \text{AND} \quad A D=B C \quad \quad$ $\text {[opposite side of a ||gm ]}$
$\therefore A B=B C=C D=D A \quad \quad \quad \text { Hence, } || \text { gm } A B C D \text { is a rhombus. }$
CIRCLES
Ex. 2 A circle touches the $B C$ of a $\triangle A B C$ at $P$ and touches $A B$ and $A C$ when produced at $Q$ and $R$ respectively as shown in figure, Show that $=\frac{1}{2}$ (Perimeter of $\triangle ABC$ ).
CIRCLES
Sol. Given : $A$ circle is touching side $B C$ of $\triangle A B C$ at $P$ and touching $A B$ and $A C$ when produced at $Q$ and $R$ respectively.
To prove : $\quad AQ=\frac{1}{2}$ (perimeter of $.\triangle ABC)$

Proof :
$ \begin{aligned} & AQ=AR …(i)\\ & BQ=BP …(ii)\\ & CP=CR …(iii) \end{aligned} $
CIRCLES
[Tangents drawn from and external point to a circle are equal]
Now, perimeter of $\triangle ABC$
$ \begin{aligned} & =A B+B C+C A \\ & =A B+B P+P C+C A \\ & =(A B+B Q)+(C R+C A)\quad \quad \text{[From (ii) and (iii)]}\\ & =A Q+A R=A Q+A Q \quad \quad \text{[From (i)]}\\ A Q=\frac{1}{2} & \text { (perimeter of } \triangle A B C) . \end{aligned} $
CIRCLES
Ex. 3 Prove that the tangents at the extremities of any chord make equal angles with the chord.
CIRCLES
Sol. Let $A B$ be a chord of a circle with centre $O$, and let AP and BP be the tangents at $A$ and $B$ respectively. Suppose, the tangents meet at point $P$. Join OP. Suppose OP meets $A B$ at $C$.
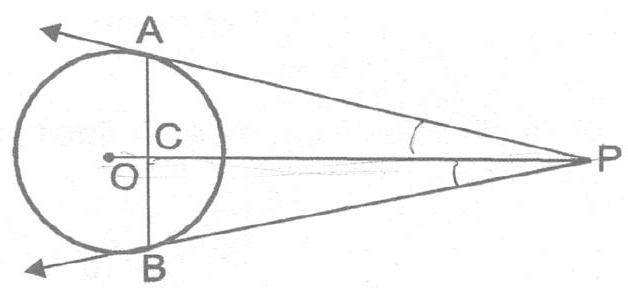
We have to prove that $ \angle PAC=\angle PBC $
In triangles PCA and PCB
$P A=P B$
CIRCLES
$[\therefore$ Tangent from an external point are equal]
$ \angle APC=\angle BPC $ $[\therefore PA$ and $PB$ are equally inclined to OP]
And $\quad P C=P C$ [Common]
So, by SAS criteria of congruence
$ \triangle PAC \cong \triangle BPC \quad \Rightarrow \quad \angle PAC=\angle PBC $
[By CPCT]
CIRCLES
Ex. 4 Prove that the segment joining the points of contact of two parallel tangents passes through the centre.
CIRCLES
Sol. Let PAQ and RBS be two parallel tangents to a circle with centre O. Join OA and OB. Draw OC||PQ Now, $PA || CO$

$ \begin{matrix} \Rightarrow & \angle PAO+\angle COA=180^{\circ} & {[\text { Sum of co-interior angle is } 180^{\circ}]} \\ \Rightarrow & 90^{\circ}+\angle COA=180^{\circ} & {[\therefore \angle PAO=90]} \\ \Rightarrow & \angle COA=90^{\circ} & \end{matrix} $
Similarly, $\angle CON=90^{\circ}$
$\therefore \quad \angle C O A+\angle C O B=90^{\circ}+90^{\circ}=180^{\circ} \quad$ Hence, $A O B$ is a straight line passing through $O$.
CIRCLES
DAILY PRACTICE PROBLEMS 9
OBJECTIVE DPP - 9.1
1. The length of the tangent drawn from a point $8 cm$ away from the centre of a circle of radius $6 cm$ is
(A) $\sqrt{7} cm$
(B) $\sqrt[2]{7} cm$
(C) $10 cm$
(D) $5 cm$
CIRCLES
| Que. | 1 |
|---|---|
| Ans. | B |
CIRCLES
2. $ A$ tangent $P Q$ at a point $P$ of a circle of radius $5 cm$ meets a line through the centre $O$ at a point $Q$, so that $O Q=12 cm$. Length of $P Q$ is :
(A) $12 cm$
(B) $13 cm$
(C) $8.5 cm$
(D) $\sqrt{119} cm$
CIRCLES
| Que. | 2 |
|---|---|
| Ans. | D |
CIRCLES
3. If tangents $P A$ and $P B$ from a point $P$ to a circle with centre $O$ are inclined to each other at an angle of $80^{\circ}$ then $\angle POA$ is equal to
(A) $50^{\circ}$
(B) $60^{\circ}$
(C) $70^{\circ}$
(D) $80^{\circ}$
CIRCLES
| Que. | 3 |
|---|---|
| Ans. | A |
CIRCLES
4. Two circle touch each other externally at $C$ and $A B$ is a common tangent to the circle. Then $\angle A C B=$
(A) $60^{\circ}$
(B) $45^{\circ}$
(C) $30^{\circ}$
(D) $90^{\circ}$
CIRCLES
| Que. | 4 |
|---|---|
| Ans. | D |
CIRCLES
5. $\quad A B C$ is a right angled triangle, right angled at $B$ such that $B C=6$ am and $A B=8 cm$. $A$ circle with centre $O$ is inscribed in $\triangle ABC$. The radius of the circle is
(A) $1 cm$
(B) $2 cm$
(C) $3 cm$
(D) $4 cm$
CIRCLES
| Que. | 5 |
|---|---|
| Ans. | B |
CIRCLES
SUBJECTIVE DPP - 9.2
1. $A B C D$ is a quadrilateral such than $\angle D=90^{\circ}$. A circle $C(O, r)$ touches the sides $A B, B C, C D$ and $D A$ at $P, Q, R$ and $S$ respectively. If $B C=38 cm, C D=25 cm$ and $B P=27 cm$, find $r$.
CIRCLES
Sol. 1. $\quad 14 cm$
CIRCLES
2. Two concentric circles are of radius $5 cm$ and $3 cm$. Find the length of the chord of the larger circle which touches the smaller circle.
CIRCLES
Sol. 2. $\quad 8 cm$
CIRCLES
3. In a circle of radius $5 cm, A B$ and $A C$ are two chords, such that $A B=A C=6 cm$. Find the length of chord BC.
CIRCLES
Sol. 3. $\quad 9.6 cm $.
CIRCLES
4. The radius of the incircle of a triangle is $4 cm$ and the segments into which one side is divided by the point of contact are $6 cm$ and $8 cm$. Determine the other two sides of the triangle.
CIRCLES
Sol. 4. $\quad 13 cm$ and $15 cm$
CIRCLES
5. In figure, $\ell$ and $m$ are two parallel tangents at $P$ and $R$. The tangent at $Q$ makes an intercept ST between $\ell$ and $m$. Prove that $\angle SOT=90^{\circ}$

CIRCLES
6. $P Q R$ is a right angled triangle with $P Q=12 cm$ and $Q R=5 cm$. A circle with centre $O$ and radius $x$ is inscribed in $\triangle P Q R$. Find the value of $x$.

CIRCLES
Sol. 6. $\quad 2 cm \quad $
CIRCLES
7. From an external point $P$, two tangents $PA$ and $PB$ are drawn to the circle with centre $O$. Prove that $OP$ is the perpendicular dissector of $A B$.
CIRCLES
8. Two tangent $T P$ and $T Q$ are drawn to a circle with centre $O$ from an external point $T$. Prove that $\angle PTQ=2 \angle OPQ$.
CIRCLES
9. A circle touches the sides of a quadrilateral $A B C D$ at $P, Q, R, S$ respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
CIRCLES
10. In figure, a circle touches all the four sides of a quadrilateral $A B C D$ with $A B=6 cm, B C=7 cm$ and $C D=$ $4 cm$. Find AD.
[CBSE - 2002]

CIRCLES
Sol. 10. $\quad 3 cm$
CIRCLES
11. Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Using the above, do the following :
In figure, $T P$ and $T Q$ are tangents from $T$ to the circle with centre $O$ and $R$ is any point on the circle. If $A B$ is a tangent to the circle at $R$, prove that
$ TA+AR=TB+BR $
[CBSE - 208]

CIRCLES
12. In figure, if $\angle A T O=40^{\circ}$, find $\angle A O B$
[CBSE - 2008]

CIRCLES
Sol. 12. $\quad 100^{0}$
CIRCLES
13. In figure $OP$ is equal to diameter of the circle. Prove that $ABP$ is an equilateral triangle.
[CBSE - 2008]






