अध्याय 09 त्रिकोणमिति के कुछ अनुप्रयोग
9.1 ऊँचाइयाँ और दूरियाँ
#missing
आइए हम अध्याय 8 में दी गई आकृति 8.1 पर विचार करें, जिसे नीचे आकृति 9.1 में पुनः खींचा गया है।

आकृति 9.1
इस आकृति में, छात्र की आँख से मीनार के शिखर तक खींची गई रेखा $\mathrm{AC}$ को दृष्टि-रेखा (line of sight) कहा जाता है। छात्र मीनार के शिखर की ओर देख रहा है। दृष्टि-रेखा और क्षैतिज रेखा से बने कोण BAC को छात्र की आँख से मीनार के शिखर का उन्नयन कोण (angle of elevation) कहा जाता है।
इस प्रकार, दृष्टि-रेखा प्रेक्षक की आँख के उस वस्तु के बिंदु को मिलाने वाली रेखा होती है जिसे प्रेक्षक देखता है। देखे गए बिंदु का उन्नयन कोण उस स्थिति में, दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है, जबकि देखा जा रहा बिंदु क्षैतिज स्तर से ऊपर होता है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपना सिर उठाना होता है। (देखिए आकृति 9.2)।

आकृति 9.2
आइए अब हम आकृति 8.2 में दी गई स्थिति पर विचार करें। बालकनी में बैठी लड़की मंदिर की सीढ़ी पर रखे गमले को नीचे की ओर देख रही है। इस स्थिति में, दृष्टि-रेखा क्षैतिज स्तर से नीचे है। दृष्टि-रेखा और क्षैतिज रेखा से इस प्रकार बने कोण को अवनमन कोण (angle of depression) कहा जाता है।
अतः देखी जा रही वस्तु पर स्थित बिंदु का अवनमन कोण उस स्थिति में दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जबकि बिंदु क्षैतिज रेखा से नीचे होता है अर्थात् वह स्थिति जबकि देखे जाने वाले बिंदु को देखने के लिए हमें अपना सिर नीचे झुकाना होता है (देखिए आकृति 9.3)।

आकृति 9.3
अब आप आकृति 8.3 में बनी दृष्टि-रेखाएँ और इस तरह बने कोणों को पहचान सकते हैं। ये कोण उन्नयन कोण हैं या अवनमन कोण?
आइए हम आकृति 9.1 को पुनः देखें। यदि आप सही मायने में बिना मापे ही मीनार की ऊँचाई $\mathrm{CD}$ ज्ञात करना चाहते हैं तो इसके लिए आपको किस जानकारी की आवश्यकता होती है? इसके लिए निम्नलिखित तथ्यों का ज्ञान होना आवश्यक होता है:
(i) दूरी $\mathrm{DE}$ जहाँ छात्र मीनार के पाद-बिंदु से इस दूरी पर खड़ा है।
(ii) मीनार के शिखर का उन्नयन कोण $\angle \mathrm{BAC}$
(iii) छात्र की ऊँचाई $\mathrm{AE}$
यह मानकर कि ऊपर बतायी गयीं तीनों जानकारियाँ हमें ज्ञात हैं तो हम किस प्रकार मीनार की ऊँचाई ज्ञात कर सकते हैं?
आकृति में $\mathrm{CD}=\mathrm{CB}+\mathrm{BD}$ यहाँ $\mathrm{BD}=\mathrm{AE}$ है जो कि छात्र की ऊँचाई है।
$\mathrm{BC}$ ज्ञात करने के लिए हम $\angle \mathrm{BAC}$ या $\angle \mathrm{A}$ के त्रिकोणमिति अनुपातों का प्रयोग करेंगे।
$\triangle \mathrm{ABC}$ में, भुजा $\mathrm{BC}$ ज्ञात कोण $\angle \mathrm{A}$ के संबंध में सम्मुख भुजा है। यहाँ हम किन-किन त्रिकोणमिति अनुपातों का प्रयोग कर सकते हैं? इनमें से किसके दो मान हमें ज्ञात है और हमें किसका मान ज्ञात करने की आवश्यकता होती है? $\tan \mathrm{A}$ या $\cot \mathrm{A}$ का प्रयोग करने से हमारी खोज का क्षेत्र कम हो जाता है, क्योंकि इन अनुपातों में $\mathrm{AB}$ और $\mathrm{BC}$ का प्रयोग होता है।
अतः $\tan \mathrm{A}=\frac{\mathrm{BC}}{\mathrm{AB}}$ या $\cot \mathrm{A}=\frac{\mathrm{AB}}{\mathrm{BC}}$, जिसे हल करने पर हमें $\mathrm{BC}$ प्राप्त हो जाएगा।
$\mathrm{BC}$ और $\mathrm{AE}$ जोड़ने पर मीनार की ऊँचाई प्राप्त हो जाएगी।
आइए अब हम कुछ उदाहरण हल करके अभी-अभी चर्चित किए गए प्रक्रम की व्याख्या करें।
उदाहरण 1 : धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिंदु से, जो मीनार के पाद-बिंदु से $15 \mathrm{~m}$ दूर है, मीनार के शिखर का उन्नयन कोण $60^{\circ}$ है। मीनार की ऊँचाई ज्ञात कीजिए।

आकृति 9.4
हल : आइए पहले हम प्रश्न को निरूपित करने के लिए एक सरल आरेख बनाएँ (देखिए आकृति 9.4)। यहाँ $\mathrm{AB}$ मीनार को निरूपित करता है, $\mathrm{CB}$ मीनार से बिंदु की दूरी है और $\angle \mathrm{ACB}$ उन्नयन कोण है। हम मीनार की ऊँचाई अर्थात् $\mathrm{AB}$ ज्ञात करना चाहते हैं और, यहाँ $\mathrm{ACB}$ एक त्रिभुज है जो $\mathrm{B}$ पर समकोण है।
प्रश्न को हल करने के लिए हम त्रिकोणमितीय अनुपात $\tan 60^{\circ}\left(य ा \cot 60^{\circ}\right)$ लेते हैं, क्योंकि इस अनुपात में $\mathrm{AB}$ और $\mathrm{BC}$ दोनों होते हैं
$\begin{array}{rlrl} & \text { अब } & \tan 60^{\circ} & =\frac{\mathrm{AB}}{\mathrm{BC}} \\ & \text { अर्थात् } & \sqrt{3} & =\frac{\mathrm{AB}}{15} \\ \text { अर्थात् }& & \mathrm{AB} & =15 \sqrt{3}\end{array}$
अतः मीनार की ऊँचाई $15 \sqrt{3} \mathrm{~m}$ है।
उदाहरण 2 : एक बिजली मिस्त्री को एक $5 \mathrm{~m}$ ऊँचे खंभे पर आ गई खराबी की मरम्मत करनी है। मरम्मत का काम करने के लिए उसे खंभे के शिखर से $1.3 \mathrm{~m}$ नीचे एक बिंदु तक वह पहुँचना चाहती है (देखिए आकृति 9.5)। यहाँ तक पहुँचने के लिए प्रयुक्त सीढ़ी की लंबाई कितनी होनी चाहिए जिससे कि क्षैतिज से $60^{\circ}$ के कोण से झुकाने पर वह अपेक्षित स्थिति तक पहुँच जाए? और यह भी बताइए कि खंभे का पाद-बिंदु कितनी दूरी पर सीढ़ी के पाद-बिंदु से होना चाहिए? (यहाँ आप $\sqrt{3}=1.73$ ले सकते हैं।)

आकृति 9.5
हल : आकृति 9.5 में, बिजली मिस्त्री को खंभे $\mathrm{AD}$ पर बिंदु $\mathrm{B}$ तक पहुँचना है।
$$ \text { अत: } \quad \mathrm{BD}=\mathrm{AD}-\mathrm{AB}=(5-1.3) \mathrm{m}=3.7 \mathrm{~m} $$
यहाँ $\mathrm{BC}$ सीढ़ी को प्रकट करता है। हमें इसकी लंबाई अर्थात् समकोण त्रिभुज $\mathrm{BDC}$ का कर्ण ज्ञात करना है।
अब, क्या आप यह बता सकते हैं कि हमें किस त्रिकोणमिति अनुपात का प्रयोग करना चाहिए?
यह त्रिकोणमिति अनुपात $\sin 60^{\circ}$ होना चाहिए।
अत: $\quad \frac{\mathrm{BD}}{\mathrm{BC}}=\sin 60^{\circ}$ या $\frac{3.7}{\mathrm{BC}}=\frac{\sqrt{3}}{2}$
इसलिए
$$ \mathrm{BC}=\frac{3.7 \times 2}{\sqrt{3}}=4.28 \mathrm{~m} \text { (लगभग) } $$
अर्थात् सीढ़ी की लंबाई $4.28 \mathrm{~m}$ होनी चाहिए।
अब
$$ \frac{\mathrm{DC}}{\mathrm{BD}}=\cot 60^{\circ}=\frac{1}{\sqrt{3}} $$
अर्थात्
$$ \mathrm{DC}=\frac{3.7}{\sqrt{3}}=2.14 \mathrm{~m} \text { (लगभग) } $$
अतः उसे सीढ़ी के पाद को खंभे से $2.14 \mathrm{~m}$ की दूरी पर रखना चाहिए।
उदाहरण 3: $ 1.5 \mathrm{~m}$ लंबा एक प्रेक्षक एक चिमनी से $28.5 \mathrm{~m}$ की दूरी पर है। उसकी आँखों से चिमनी के शिखर का उन्नयन कोण $45^{\circ}$ है। चिमनी की ऊँचाई बताइए।
हल : यहाँ $\mathrm{AB}$ चिमनी है, $\mathrm{CD}$ प्रेक्षक है और $\angle \mathrm{ADE}$ उन्नयन कोण है (देखिए आकृति 9.6)। यहाँ $\mathrm{ADE}$ एक त्रिभुज है जिसमें कोण $\mathrm{E}$ समकोण है और हमें चिमनी की ऊँचाई ज्ञात करनी है।

आकृति 9.6
यहाँ
$$ \mathrm{AB}=\mathrm{AE}+\mathrm{BE}=(\mathrm{AE}+1.5) \mathrm{m} $$
और
$$ \mathrm{DE}=\mathrm{CB}=28.5 \mathrm{~m} $$
$\mathrm{AE}$ ज्ञात करने के लिए हमें एक ऐसा त्रिकोणमिति अनुपात लेना चाहिए जिसमें $\mathrm{AE}$ और $\mathrm{DE}$ दोनों हो। इसके लिए आइए हम उन्नयन कोण का tangent लें।
अब
$$ \tan 45^{\circ}=\frac{\mathrm{AE}}{\mathrm{DE}} $$
अर्थात्
$$ 1=\frac{\mathrm{AE}}{28.5} $$
इसलिए
$$ \mathrm{AE}=28.5 $$
अतः चिमनी की ऊँचाई $(\mathrm{AB})=(28.5+1.5) \mathrm{m}=30 \mathrm{~m}$
उदाहरण 4 : भूमि के एक बिंदु $P$ से एक $10 \mathrm{~m}$ ऊँचे भवन के शिखर का उन्नयन कोण $30^{\circ}$ है। भवन के शिखर पर एक ध्वज को लहराया गया है और $P$ से ध्वज के शिखर का उन्नयन कोण $45^{\circ}$ है। ध्वजदंड की लंबाई और बिंदु $\mathrm{P}$ से भवन की दूरी ज्ञात कीजिए। (यहाँ आप $\sqrt{3}=1.732$ ले सकते हैं।)
हल : आकृति 9.7 में, $\mathrm{AB}$ भवन की ऊँचाई प्रकट करता है, $\mathrm{BD}$ ध्वजदंड प्रकट करता है और $\mathrm{P}$ दिया हुआ बिंदु प्रकट करता है। ध्यान दीजिए कि यहाँ दो समकोण त्रिभुज PAB और $\mathrm{PAD}$ हैं। हमें ध्वजदंड की लंबाई अर्थात् $\mathrm{DB}$ और बिंदु $\mathrm{P}$ से भवन की दूरी अर्थात् $\mathrm{PA}$ ज्ञात करना है।

आकृति 9.7
क्योंकि हमें भवन की ऊँचाई $\mathrm{AB}$ ज्ञात है इसलिए पहले हम समकोण $\triangle \mathrm{PAB}$ लेंगे।
यहाँ
$$ \tan 30^{\circ}=\frac{\mathrm{AB}}{\mathrm{AP}} $$
अर्थात्
$$ \frac{1}{\sqrt{3}}=\frac{10}{\mathrm{AP}} $$
इसलिए
$$ \mathrm{AP}=10 \sqrt{3} $$
अर्थात् $P$ से भवन की दूरी $10 \sqrt{3} \mathrm{~m}=17.32 \mathrm{~m}$
आइए अब हम यह मान लें कि $\mathrm{DB}=x \mathrm{~m}$ है तब $\mathrm{AD}=(10+x) \mathrm{m}$
अब समकोण $\triangle \mathrm{PAD}$ में
$$ \tan 45^{\circ}=\frac{\mathrm{AD}}{\mathrm{AP}}=\frac{10+x}{10 \sqrt{3}} $$
इसलिए
$$ 1=\frac{10+x}{10 \sqrt{3}} $$
अर्थात्
$$ x=10(\sqrt{3}-1)=7.32 $$
अतः ध्वजदंड की लंबाई $7.32 \mathrm{~m}$ है।
उदाहरण 5 : एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में $40 \mathrm{~m}$ अधिक लंबी हो जाती है जबकि सूर्य का उन्नतांश (altitude) $60^{\circ}$ से घटकर $30^{\circ}$ हो जाता है अर्थात् छाया के एक सिरे से मीनार के शिखर का उन्नयन कोण $60^{\circ}$ है और $\mathrm{DB}$ छाया की लंबाई है जबकि उन्नयन कोण $30^{\circ}$ है। मीनार की ऊँचाई ज्ञात कीजिए।
हल : मान लीजिए कि $\mathrm{AB}$ की लंबाई $h$ मीटर है और $\mathrm{BC}, x$ मीटर है। प्रश्न के अनुसार $\mathrm{DB}, \mathrm{BC}$ से $40 \mathrm{~m}$ अधिक लंबा है।

आकृति 9.8
#missing
अत:
$$ \quad \mathrm{DB}=(40+x) \mathrm{m} $$
अब, यहाँ दो समकोण त्रिभुज $\mathrm{ABC}$ और $\mathrm{ABD}$ है।
$\begin{array}{rlrl}\Delta \mathrm{ABC} \text { में } & \tan 60^{\circ} & =\frac{\mathrm{AB}}{\mathrm{BC}} \\ & \text { या } & \sqrt{3} & =\frac{h}{x} \\ \Delta \mathrm{ABD} & \text { में } & \tan 30^{\circ} & =\frac{\mathrm{AB}}{\mathrm{BD}} \\ & \text { अर्थात् } & \frac{1}{\sqrt{3}} & =\frac{h}{x+40}\end{array}$
(1) से हमें यह प्राप्त होता है
$$ h=x \sqrt{3} $$
इस मान को (2) में प्रतिस्थापित करने पर हमें यह प्राप्त होता है $(x \sqrt{3}) \sqrt{3}=x+40$, अर्थात् $3 x=x+40$
$$ \begin{align*} \text{ अर्थात् } \qquad\qquad & x=20 \\ \text{ इसलिए }\qquad\qquad & h=20 \sqrt{3} \tag{1 से } \end{align*} $$
अतः मीनार की ऊँचाई $20 \sqrt{3} \mathrm{~m}$ है।
उदाहरण 6 : एक बहुमंजिल भवन के शिखर से देखने पर एक $8 \mathrm{~m}$ ऊँचे भवन के शिखर और तल के अवनमन-कोण क्रमशः $30^{\circ}$ और $45^{\circ}$ हैं। बहुमंजिल भवन की ऊँचाई और दो भवनों के बीच की दूरी ज्ञात कीजिए।
हल : आकृति 9.9 में $\mathrm{PC}$ बहुमंजिल भवन को और $\mathrm{AB}, 8 \mathrm{~m}$ ऊँचे भवन को प्रकट करता है। हम बहुमंजिल भवन की ऊँचाई, अर्थात् $\mathrm{PC}$ और दो भवनों के बीच की दूरी अर्थात् $\mathrm{AC}$ ज्ञात करना चाहते हैं। आकृति को अच्छी तरह देखिए। आप यहाँ देखेंगे कि $\mathrm{PB}$ समांतर रेखाओं $\mathrm{PQ}$ और $\mathrm{BD}$ की एक तिर्यक-छेदी रेखा है। अतः $\angle \mathrm{QPB}$ और $\angle \mathrm{PBD}$ एकांतर कोण हैं और इसलिए बराबर हैं। अतः $\angle \mathrm{PBD}=30^{\circ}$, इसी प्रकार, $\angle \mathrm{PAC}=45^{\circ}$ समकोण $\triangle \mathrm{PBD}$ में

आकृति 9.9
$$\frac{\mathrm{PD}}{\mathrm{BD}}=\tan 30^{\circ}=\frac{1}{\sqrt{3}} \text { या } \mathrm{BD}=\mathrm{PD} \sqrt{3}$$
समकोण $\triangle \mathrm{PAC}$ में हम पाते हैं
$ \frac{\mathrm{PC}}{\mathrm{AC}}=\tan 45^{\circ}=1 $
$ \text { अर्थात् } \quad \mathrm{PC}=\mathrm{AC} $
और $\quad \mathrm{PC}=\mathrm{PD}+\mathrm{DC}$ इसलिए $\mathrm{PD}+\mathrm{DC}=\mathrm{AC}$
क्योंकि $\mathrm{AC}=\mathrm{BD}$ और $\mathrm{DC}=\mathrm{AB}=8 \mathrm{~m}$, इसलिए $\mathrm{PD}+8=\mathrm{BD}=\mathrm{PD} \sqrt{3}$ (क्यों?)
इससे यह प्राप्त होता है:
$\mathrm{PD}=\frac{8}{\sqrt{3}-1}=\frac{8(\sqrt{3}+1)}{(\sqrt{3}+1)(\sqrt{3}-1)}=4(\sqrt{3}+1) \mathrm{m}$
अतः बहुमंजिल भवन की ऊँचाई ${4(\sqrt{3}+1)+8} \mathrm{m}=4(3+\sqrt{3}) \mathrm{m}$ है और दो भवनों के बीच की दूरी भी $4(3+\sqrt{3}) \mathrm{m}$ है।
उदाहरण 7 : एक नदी के पुल के एक बिंदु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः $30^{\circ}$ और $45^{\circ}$ हैं। यदि पुल किनारों से $3 \mathrm{~m}$ की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात कीजिए।
हल : आकृति 9.10 में, $\mathrm{A}$ और $\mathrm{B}$ नदी के सम्मुख किनारों के बिंदुओं को प्रकट करते हैं, जिससे कि $\mathrm{AB}$ नदी की चौड़ाई है। $3 \mathrm{~m}$ की ऊँचाई पर बने पुल पर एक बिंदु $\mathrm{P}$ है अर्थात् $\mathrm{DP}=3 \mathrm{~m}$ है। हम नदी की चौड़ाई ज्ञात करना चाहते हैं जो कि $\triangle \mathrm{APB}$ की भुजा $\mathrm{AB}$ की लंबाई है।

आकृति 9.10
अब
$$ \mathrm{AB}=\mathrm{AD}+\mathrm{DB} $$
समकोण $\triangle \mathrm{APD}$ में $\angle \mathrm{A}=30^{\circ}$
अत : $\quad \tan 30^{\circ}=\frac{\mathrm{PD}}{\mathrm{AD}}$
अर्थात् $\quad\quad\quad \frac{1}{\sqrt{3}}=\frac{3}{\mathrm{AD}} \text { या } \mathrm{AD}=3 \sqrt{3} \mathrm{~m}$
अतः समकोण $\triangle \mathrm{PBD}$ में, $\angle \mathrm{B}=45^{\circ}$ है। इसलिए $\mathrm{BD}=\mathrm{PD}=3 \mathrm{~m}$
अब
$ \mathrm{AB}=\mathrm{BD}+\mathrm{AD}=3+3 \sqrt{3}=3(1+\sqrt{3}) \mathrm{m} $
इसलिए नदी की चौड़ाई $3(\sqrt{3}+1) \mathrm{m}$ है।
प्रश्नावली 9.1
1. सर्कस का एक कलाकार एक $20 \mathrm{~m}$ लंबी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंधा हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण $30^{\circ}$ का हो तो खंभे की ऊँचाई ज्ञात कीजिए (देखिए आकृति 9.11)।
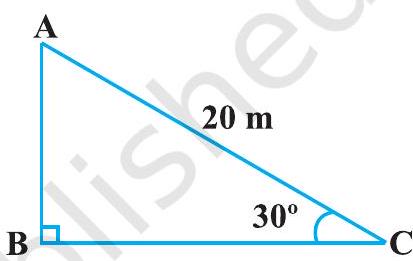
आकृति 9.11
Show Answer
#missing2. आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ $30^{\circ}$ का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, $8 \mathrm{~m}$ है। पेड़ की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing3. एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर $1.5 \mathrm{~m}$ की ऊँचाई पर हो और भूमि के साथ $30^{\circ}$ के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह $3 \mathrm{~m}$ की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ $60^{\circ}$ का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
Show Answer
#missing4. भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से $30 \mathrm{~m}$ की दूरी पर है, मीनार के शिखर का उन्नयन कोण $30^{\circ}$ है। मीनार की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing5. भूमि से $60 \mathrm{~m}$ की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध दिया गया है। भूमि के साथ डोरी का झुकाव $60^{\circ}$ है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
Show Answer
#missing6. $1.5 \mathrm{~m}$ लंबा एक लड़का $30 \mathrm{~m}$ ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण $30^{\circ}$ से $60^{\circ}$ हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।
Show Answer
#missing7. भूमि के एक बिंदु से एक $20 \mathrm{~m}$ ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः $45^{\circ}$ और $60^{\circ}$ है। मीनार की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing8. एक पेडस्टल के शिखर पर एक $1.6 \mathrm{~m}$ ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण $60^{\circ}$ है और उसी बिंदु से पेडस्टल के शिखर का उन्नयन कोण $45^{\circ}$ है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing9. एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण $30^{\circ}$ है और भवन के पाद-बिंदु से मीनार के शिखर का उन्नयन कोण $60^{\circ}$ है। यदि मीनार $50 \mathrm{~m}$ ऊँची हो, तो भवन की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing10. एक $80 \mathrm{~m}$ चौड़ी सड़क के दोनों ओर आमने-सामने समान लंबाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बीच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमशः $60^{\circ}$ और $30^{\circ}$ है। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
Show Answer
#missing11. एक नहर के एक तट पर एक टीवी टॉवर ऊर्ध्वाधरतः खड़ा है। टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण $60^{\circ}$ है। इसी तट पर इस बिंदु से $20 \mathrm{~m}$ दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण $30^{\circ}$ है। (देखिए आकृति 9.12)। टॉवर की ऊँचाई और नहर की चौड़ाई ज्ञात कीजिए।
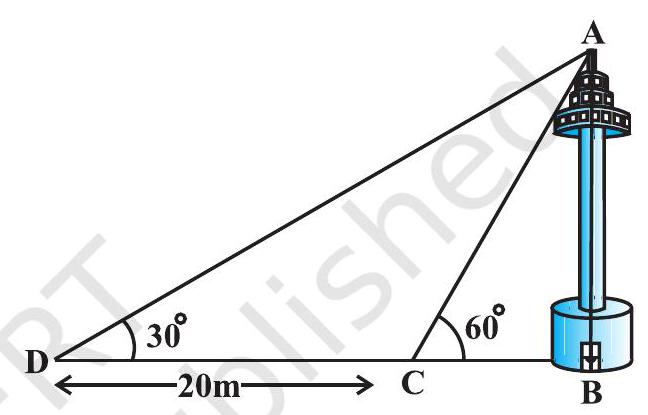
आकृति 9.12
Show Answer
#missing12. $7 \mathrm{~m}$ ऊँचे भवन के शिखर से एक केबल टॉवर के शिखर का उन्नयन कोण $60^{\circ}$ है और इसके पाद का अवनमन कोण $45^{\circ}$ है। टॉवर की ऊँचाई ज्ञात कीजिए।
Show Answer
#missing13. समुद्र-तल से $75 \mathrm{~m}$ ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण $30^{\circ}$ और $45^{\circ}$ हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
Show Answer
#missing14. $1.2 \mathrm{~m}$ लंबी एक लड़की भूमि से 88.2 $\mathrm{m}$ की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण $60^{\circ}$ है। कुछ समय बाद उन्नयन कोण घटकर $30^{\circ}$ हो जाता है (देखिए आकृति 9.13)। इस अंतराल के दौरान गुब्बारे द्वारा तय की गई दूरी ज्ञात कीजिए।
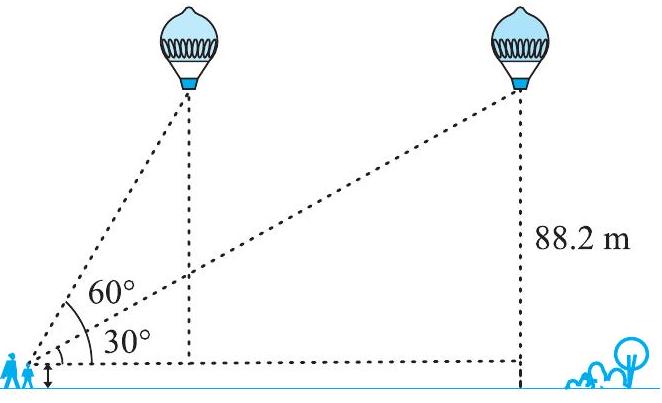
आकृति 9.13
Show Answer
#missing15. एक सीधा राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को $30^{\circ}$ के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एक समान चाल से जाता है। छः सेकेंड बाद कार का अवनमन कोण $60^{\circ}$ हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
Show Answer
#missing9.2 सारांश
इस अध्याय में, आपने निम्नलिखित तथ्यों का अध्ययन किया है :
1. (i) दृष्टि-रेखा प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिंदु को मिलाने वाली रेखा होती है।
(ii) देखी गई वस्तु का उन्नयन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जबकि यह क्षैतिज स्तर से ऊपर होता है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपने सिर को ऊपर उठाना होता है।
(iii) देखी गई वस्तु का अवनमन कोण दृष्टि-रेखा और क्षैतिज रेखा से बना कोण होता है जबकि क्षैतिज रेखा क्षैतिज स्तर से नीचे होती है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपने सिर को झुकाना पड़ता है।
2. त्रिकोणमितीय अनुपातों की सहायता से किसी वस्तु की ऊँचाई या लंबाई या दो सुदूर वस्तुओं के बीच की दूरी ज्ञात की जा सकती है।





