Let the relation of knowledge to real life be very visible to your pupils and let them understand how by knowledge the world could be transformed". - BERTRAND RUSSELL

10.1 भूमिका (Introduction)

पिछले अध्याय में हमने एक रेखा के समीकरणों के विभिन्न रूपों का अध्ययन किया है। इस अध्याय में, हम कुछ अन्य वक्रों का अध्ययन करेंगे जैसे वृत्त (circle), परवलय (parabola), दीर्घवृत्त (ellipse) और अतिपरवलय (hyperbola)। परवलय और अतिपरवलय Apollonius द्वारा दिए गए नाम हैं। वास्तव में इन वक्रों को शंकु परिच्छेद या सामान्यतः शांकव कहा जाता है क्योंकि इन्हें एक लंब वृत्तीय द्विशंकु और एक समतल के परिच्छेदन से प्राप्त किया जा सकता है। इन वक्रों का ग्रहों के घूर्णन, दूरदर्शीयंत्र (telescope) और एंटीना के निर्माण, आटोमोबाइल्स की हेडलाइट में, परावर्तक इत्यादि में बहुत अधिक उपयोगी होता है।

Apollonius (262 B.C. -190 B.C.)

अब हम आगे आने वाले अनुभागों में देखेंगें कि किस प्रकार एक लंब वृत्तीय द्विशंकु और एक तल के परिच्छेदन के परिणाम स्वरूप विभिन्न प्रकार के वक्र प्राप्त होते हैं।

10.2 शंकु के परिच्छेद

मान लीजिए $l$ एक स्थिर ऊर्ध्वाधर रेखा है $m$ एक दूसरी रेखा है जो इस रेखा को स्थिर बिंदु $\mathrm{V}$ पर प्रतिच्छेद करती है और इससे एक कोण $\alpha$ बनाती है (आकृति 10.1)।

आकृति 10.1

मान लीजिए हम रेखा $m$ को रेखा $l$ के परितः इस प्रकार घुमाते हैं कि $m$ की सभी स्थितियों में, कोण $\alpha$ अचर रहे तब उत्पन्न पृष्ठ एक लंब वृत्तीय खोखले द्विशंकु है जिन्हें अब से शंकु कहेंगे जो दोनों दिशाओं में अनिश्चित दूरी तक बढ़ रहे हैं (आकृति 10.2)।

आकृति 10.2

स्थिर बिंदु $\mathrm{V}$ को शंकु का शीर्ष (vertex) और स्थिर रेखा $l$ शंकु का अक्ष (axis) कहलाता है। इन सभी स्थितियों में घूमने वाली रेखा $m$ शंकु की जनक (generator) कहलाती है। शंकु को शीर्ष दो भागों में विभक्त करता है जिन्हें नापे (Nappes) कहते हैं।

यदि हम एक तल और एक शंकु का परिच्छेदन लेते हैं तो इस प्रकार प्राप्त परिच्छेद वक्र, शंकु परिच्छेद कहलाते हैं। इस प्रकार, शंकु परिच्छेद वे वक्र हैं जिन्हें एक लंब वृत्तीय शंकु और एक तल के परिच्छेदन से प्राप्त किया जाता है।

शंकु के ऊर्ध्वाधर अक्ष और परिच्छेदी तल के बीच बने कोण और परिच्छेदी तल की स्थितियों के अनुसार विभिन्न प्रकार के शंकु परिच्छेद प्राप्त होते हैं। मान लीजिए परिच्छेदी तल, शंकु के ऊर्ध्वाधर अक्ष के साथ $\beta$ कोण बनाता है (आकृति 10.3)।

आकृति 10.3

शंकु के साथ तल का परिच्छेदन या तो शंकु के शीर्ष पर हो सकता है या नापे के दूसरे किसी भाग पर ऊपर या नीचे हो सकता हैं।

10.2.1 वृत्त, दीर्घवृत्त, परवलय और अतिपरवलय (Circle, ellipse, parabola and hyperbola)

जब तल, शंकु के नापे (शीर्ष के अतिरिक्त) को काटता है, तो हमें निम्नांकित स्थितियाँ प्राप्त होती हैं:

(a) जब $\beta=90^{\circ}$, तो परिच्छेद एक वृत्त होता है (आकृति 10.4)।

आकृति 10.4

(b) जब $\alpha<\beta<90^{\circ}$, तो परिच्छेद एक दीर्घवृत्त होता है (आकृति 10.5)।

आकृति 10.5

(c) जब $\beta=\alpha$, तो परिच्छेद एक परवलय होता है (आकृति 10.6)।

आकृति 10.6

(उपरोक्त तीनों स्थितियों की प्रत्येक स्थिति में तल शंकु को नापे के पूर्णतः आर-पार काटता है)।

(d) जब $0 \leq \beta<\alpha$, तो तल शंकु के दोनों नेप्स को काटता है तो परिच्छेद वक्र एक अतिपरवलय होता है (आकृति 10.7)।

आकृति 10.7

10.2.2 अपभ्रष्ट शंकु परिच्छेद (Degenerated conic sections)

जब तल शंकु के शीर्ष पर काटता है तो निम्नलिखित स्थितियाँ प्राप्त होती हैं:

(a) जब $\alpha<\beta \leq 90^{\circ}$, तो परिच्छेद एक बिंदु है (आकृति 10.8)।

आकृति 10.8

(b) जब $\beta=\alpha$, तो तल, जनक को अंतर्विष्ट करता है और परिच्छेद एक सरल रेखा होती है (आकृति 10.9)।

आकृति 10.9

यह परवलय की अपभ्रष्ट स्थिति है।

(c) जब $0 \leq \beta<\alpha$, तो परिच्छेद एक प्रतिच्छेद करने वाली रेखाओं का युग्म है (आकृति 10.10)। यह अतिपरवलय की अपभ्रष्ट स्थिति है।

आकृति 10.10 (a)

आकृति 10.10 (b)

आगे आने वाले अनुच्छेद में हम इन शंकु परिच्छेदों को ज्यामितीय गुणों के आधार पर परिभाषित करते हुए उनमें से प्रत्येक के समीकरण मानक रूप में प्राप्त करेंगे।

10.3 वृत्त (Circle)

परिभाषा 1 वृत्त, तल के उन बिंदुओं का समुच्चय होता है जो तल के एक स्थिर बिंदु से समान दूरी पर होते हैं।

स्थिर बिंदु को वृत्त का केंद्र (centre) कहते हैं तथा वृत्त पर किसी एक बिंदु की केंद्र से दूरी को वृत्त की त्रिज्या (radius) कहते हैं (आकृति 10.11)।

आकृति 10.11

यदि वृत्त का केंद्र मूल बिंदु पर होता है तो वृत्त का समीकरण सरलतम होता है। फिर भी, हम ज्ञात केंद्र तथा त्रिज्या के वृत्त का समीकरण निम्नलिखित प्रकार से व्युत्पन्न करेंगें (आकृति 10.12)।

आकृति 10.12

वृत्त का केंद्र $\mathrm{C}(h, k)$ तथा त्रिज्या $r$ ज्ञात है। मान लीजिए वृत्त पर कोई बिंदु $\mathrm{P}(x, y)$ है (आकृति 10.12)। तब परिभाषा से, $|\mathrm{CP}|=r$ दूरी सूत्र द्वारा, हम पाते हैं

अर्थात्

$ \begin{aligned} & \sqrt{(x-h)^{2}+-k)^{2}}=r & (x-h)^{2}+(y-k)^{2}=r^{2} \end{aligned} $

यह केंद्र $(h, k)$ तथा त्रिज्या $r$ वाले वृत्त का अभीष्ट समीकरण है।

उदाहरण 1 केंद्र $(0,0)$ तथा त्रिज्या $r$ वाले वृत्त का समीकरण ज्ञात कीजिए।

हल यहाँ $h=k=0$. अतः वृत्त का समीकरण $x^{2}+y^{2}=r^{2}$ है।

उदाहरण 2 केंद्र $(-3,2)$ तथा त्रिज्या 4 इकाई वाले वृत्त का समीकरण ज्ञात कीजिए।

हल यहाँ $h=-3, k=2$ और $r=4$. अतः वृत्त का अभीष्ट समीकरण

$$ (x+3)^{2}+(y-2)^{2}=16 \text { है। } $$

उदाहरण 3 वृत्त $x^{2}+y^{2}+8 x+10 y-8=0$ का केंद्र तथा त्रिज्या ज्ञात कीजिए।

हल दिया गया समीकरण

$$ \left(x^{2}+8 x\right)+\left(y^{2}+10 y\right)=8 $$

अब कोष्ठकों को पूर्ण वर्ग बनाने पर,

या $ (x^{2}+8 x+16)+(y^{2}+10 y+25)=8+16+25 $

या

$ (x+4)^{2}+(y+5)^{2}=49 $

या

$ {x-(-4)}^{2}+{y-(-5)}^{2}=7^{2} $

अतः वृत्त का केंद्र $(-4,-5)$ व त्रिज्या 7 इकाई है।

उदाहरण 4 बिंदुओं $(2,-2)$, और $(3,4)$ से होकर जाने वाले उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखा $x+y=2$ पर स्थित है।

हल मान लीजिए कि वृत्त का समीकरण $(x-h)^{2}+(y-k)^{2}=r^{2}$ है।

यह बिंदुओं $(2,-2)$ और $(3,4)$ से जाता है। इसलिए हम पाते हैं कि

$$ \begin{equation*} (2-h)^{2}+(-2-k)^{2}=r^{2} \tag{1} \end{equation*} $$

और $$ \begin{equation*} (3-h)^{2}+(4-k)^{2}=r^{2} \tag{2} \end{equation*} $$

तथा वृत्त का केंद्र रेखा $x+y=2$, पर स्थित है, इसलिए

$$ \begin{equation*} h+k=2 \tag{3} \end{equation*} $$

समीकरण (1), (2) व (3), को हल करने पर, हम पाते हैं कि

$$ h=0.7, \quad k=1.3 \text { और } r^{2}=12.58 $$

अतः वृत्त का अभीष्ट समीकरण

$$ (x-0.7)^{2}+(y-1.3)^{2}=12.58 $$

प्रश्नावली 10.1

निम्नलिखित प्रश्न 1 से 5 तक प्रत्येक में वृत्त का समीकरण ज्ञात कीजिए:

1. केंद्र $(0,2)$ और त्रिज्या 2 इकाई

Show Answer

\misisng

2. केंद्र $(-2,3)$ और त्रिज्या 4 इकाई

Show Answer

\misisng

3. केंद्र $(\frac{1}{2}, \frac{1}{4})$ और त्रिज्या $\frac{1}{12}$

Show Answer

\misisng

4. केंद्र $(-a,-b)$ और त्रिज्या $\sqrt{a^{2}-b^{2}}$ है।

Show Answer

\misisng

5. केंद्र $(-a,-b)$ और त्रिज्या $\sqrt{a^{2}-b^{2}}$

Show Answer

\misisng

6. $(x+5)^{2}+(y-3)^{2}=36$

Show Answer

\misisng

7. $x^{2}+y^{2}-4 x-8 y-45=0$

Show Answer

\misisng

8. $x^{2}+y^{2}-8 x+10 y-12=0$

Show Answer

\misisng

9. $2 x^{2}+2 y^{2}-x=0$

Show Answer

\misisng

10. बिंदुओं $(4,1)$ और $(6,5)$ से जाने वाले वृत्त का समीकरण कीजिए जिसका केंद्र रेखा $4 x+y=16$ पर स्थित है।

Show Answer

\misisng

11. बिंदुओं $(2,3)$ और $(-1,1)$ से जाने वाले वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र रेखा $x-3 y-11=0$ पर स्थित है।

Show Answer

\misisng

12. त्रिज्या 5 के उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंन्द्र $x$-अक्ष पर हो और जो बिंदु $(2,3)$ से जाता है।

Show Answer

\misisng

13. $(0,0)$ से होकर जाने वाले वृत्त का समीकरण ज्ञात कीजिए जो निर्देशांक्षों पर $a$ और $b$ अंतःखण्ड बनाता है।

Show Answer

\misisng

14. उस वृत्त का समीकरण ज्ञात कीजिए जिसका केंद्र $(2,2)$ हो तथा बिंदु $(4,5)$ से जाता है।

Show Answer

\misisng

15. क्या बिंदु $(-2.5,3.5)$ वृत्त $x^{2}+y^{2}=25$ के अंदर, बाहर या वृत्त पर स्थित है ?

Show Answer

\misisng

10.4 परवलय (Parabola)

परिभाषा 2 एक परवलय तल के उन सभी बिंदुओं का समुच्चय है जो एक निश्चित सरल रेखा और तल के एक निश्चित बिंदु (जो रेखा पर स्थित नहीं है) से समान दूरी पर है।

निश्चित सरल रेखा को परवलय की नियता (directrix) और निश्चित बिंदु $\mathrm{F}$ को परवलय की नाभि (focus) कहते हैं (आकृति 10.13)। (अंग्रेजी भाषा में ‘Para’ का अर्थ ‘से’ व ‘bola’ का अर्थ ‘फेंकना’, अर्थात् हवा में गेंद फेंकने से बना हुआ पथ)

आकृति 10.13

टिप्पणी यदि निश्चित बिंदु, निश्चित सरल रेखा पर स्थित हो तो तल के उन बिंदुओं का समुच्चय जो निश्चित बिंदु और निश्चित रेखा से समान दूरी पर हैं, निश्चित बिंदु से गुज़रने वाली निश्चित रेखा पर लंबवत सरल रेखा होती है। हम इस सरल रेखा को परवलय की अपभ्रष्ट स्थिति कहते हैं।

परवलय की नाभि से जाने वाली तथा नियता पर लंब रेखा को परवलय का अक्ष कहा जाता है। परवलय का अक्ष जिस बिंदु पर परवलय को काटता है उसे परवलय का शीर्ष(vertex) कहते हैं (आकृति 10.14)।

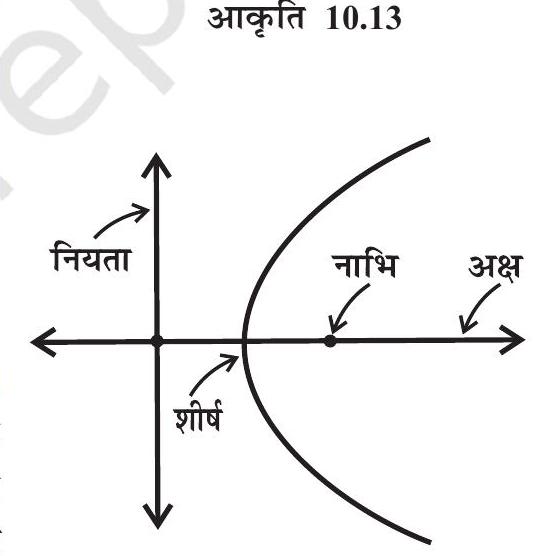
आकृति 10.14

10.4.1 परवलय का प्रमाणिक समीकरण (Standard equation of parabola)

परवलय का समीकरण सरलतम होता है यदि इसका शीर्ष मूल बिंदु पर हो और इसकी सममित अक्ष, $x$-अक्ष या $y$-अक्ष के अनुदिश होता है। परवलय के ऐसे चार संभव दिक्विन्यास नीचे आकृति $10.15(\mathrm{a})$ से $(\mathrm{d})$ तक में दर्शाए गए हैं।

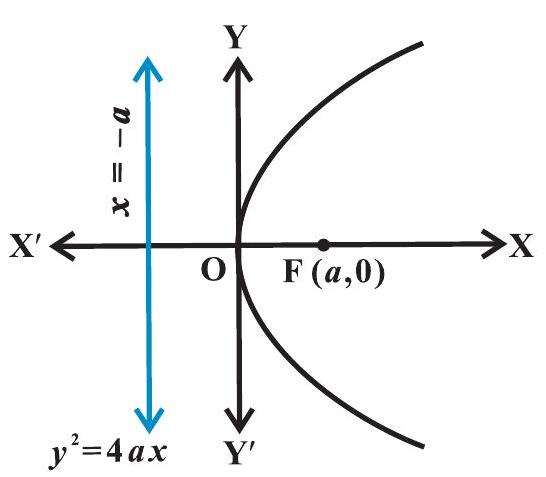
(a)

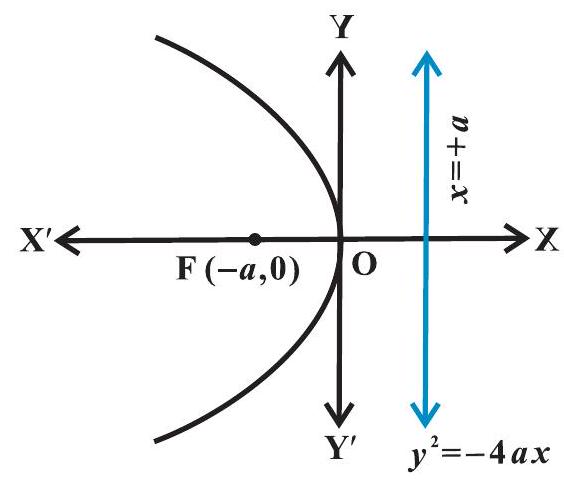
(b)

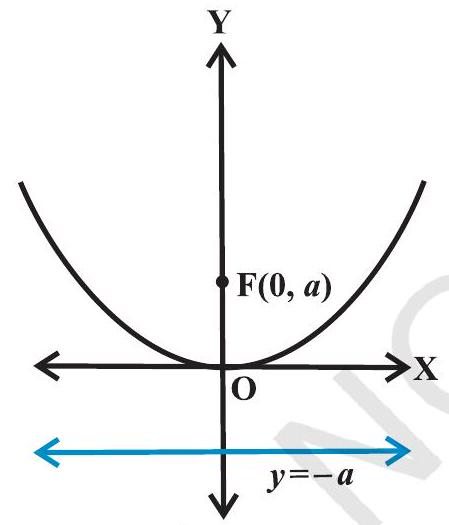
$x^{2}=4 a y$

(c)

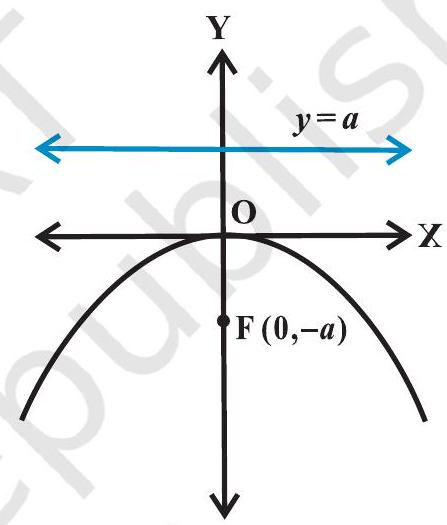
$x^{2}=-4 a y$

(d)

अब हम आकृति 10.15 (a) में दर्शाए गए परवलय का समीकरण जिसकी नाभि $(a, 0) a>$ 0 और नियता $x=-a$ को निम्नवत प्राप्त करेंगे।

मान लीजिए कि नाभि $\mathrm{F}$ और नियता $l$ है। नियता पर लंब FM खींचिए और $\mathrm{FM}$ को बिंदु $\mathrm{O}$ पर समद्विभाजित कीजिए। $M O$ को $X$ तक बढ़ाइए। परवलय की परिभाषा के अनुसार मध्य बिंदु $\mathrm{O}$ परवलय पर है और परवलय का शीर्ष कहलाता है। $\mathrm{O}$ को मूल बिंदु मानकर $\mathrm{OX}$ को $x$-अक्ष और इसके लंबवत $\mathrm{OY}$ को $y$-अक्ष लीजिए। मान लीजिए कि नाभि की नियता से दूरी $2 a$ है। तब नाभि के निर्देशांक $(a, 0), a>0$ है तथा नियता का समीकरण $x+a=0$ जैसा कि आकृति 10.16 में है।

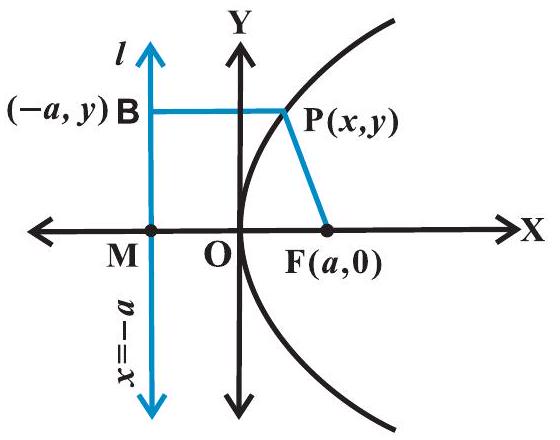
आकृति $\mathbf{1 0 . 1 6}$

मान लीजिए परवलय पर कोई बिंदु $\mathrm{P}(x, y)$ इस प्रकार है कि

$ \begin{equation*} P F=P B \tag{1} \end{equation*} $

जहाँ $\mathrm{PB}$ रेखा $l$ पर लंब है। $\mathrm{B}$ के निर्देशांक $(-a, y)$ हैं। दूरी सूत्र से हम पाते हैं

$ \mathrm{PF}=\sqrt{(x-a)^{2}+y^{2}} \text { और } \mathrm{PB}=\sqrt{(x+a)^{2}} $

क्योंकि $\mathrm{PF}=\mathrm{PB}$, हम पाते हैं,

$ \sqrt{(x-a)^{2}+y^{2}}=\sqrt{(x+a)^{2}} $

इसलिए $ \quad\quad\quad(x-a)^{2}+y^{2}=(x+a)^{2}$

या $\quad\quad\quad x^{2}-2 a x+a^{2}+y^{2}=x^{2}+2 a x+a^{2}$

या $\quad\quad\quad y^{2}=4 a x(a>0)$.

इस प्रकार परवलय पर कोई बिंदु समीकरण

$ \begin{equation*} y^{2}=4 a x \text { को संतुष्ट करता है। } \tag{2} \end{equation*} $

विलोमतः माना $(2)$ पर $\mathrm{P}(x, y)$ एक बिंदु है।

अब $ \begin{align*} \mathrm{PF} & =\sqrt{(x-a)^{2}+y^{2}}=\sqrt{(x-a)^{2}+4 a x} \\ & =\sqrt{(x+a)^{2}}=\mathrm{PB} \tag{3} \end{align*} $

इसलिए $\mathrm{P}(x, y)$, परवलय पर स्थित है।

इस प्रकार (2) और (3) से हमने सिद्ध किया कि एक परवलय जिसका शीर्ष मूल बिंदु पर नाभि $(a, 0)$ तथा नियता $x=-a$ का समीकरण $y^{2}=4 a x$ होता है।

विवेचना समीकरण (2) में, यदि $a>0, x$ का मान धनात्मक या शून्य हो सकता है परंतु ऋणात्मक नहीं। इस स्थिति में परवलय को प्रथम और चतुर्थ चतुर्थांश में अनिश्चित रूप से दूर तक बढ़ाया जा सकता है और परवलय का अक्ष, $x$-अक्ष का धनात्मक भाग है।

इसी प्रकार हम परवलयों का समीकरण प्राप्त कर सकते हैं।

आकृति $10.15(\mathrm{~b})$ में $y^{2}=-4 a x$,

आकृति $10.15(\mathrm{c})$ में $x^{2}=4 a y$,

आकृति $10.15(\mathrm{~d})$ में $x^{2}=-4 a y$,

इन चार समीकरणों को परवलय के मानक समीकरण कहते हैं।

टिप्पणी परवलय के मानक समीकरण में, परवलय की नाभि किसी एक निर्देशांक अक्ष पर स्थित होती है, शीर्ष मूल बिंदु पर होता है और नियता, दूसरे अक्ष के समांतर होती है। यहाँ ऐसे परवलयों का अध्ययन, जिनकी नाभि कोई भी बिंदु हो सकती है और नियता कोई भी रेखा हो सकती है, इस पुस्तक के विषय से बाहर है।

आकृति 10.15 , से प्राप्त परवलय के प्रमाणिक समीकरण के निरीक्षण से निम्नांकित निष्कर्ष प्राप्त होते हैं:

1. परवलय, परवलय अक्ष के सापेक्ष सममित होता है। यदि परवलय के समीकरण में $y^{2}$ का पद है तो सममित, $x$-अक्ष के अनुदिश है और यदि समीकरण में $x^{2}$ का पद है तो सममित अक्ष, $y$-अक्ष के अनुदिश है।

2. यदि सममित अक्ष, $x$-अक्ष के अनुदिश हो और

(a) $x$ का गुणांक धनात्मक हो तो परवलय दाईं ओर खुलता है।

(b) $x$ का गुणांक ऋणात्मक हो तो परवलय बाईं ओर खुलता है।

3. यदि सममित अक्ष, $y$-अक्ष के अनुदिश हो और

(a) $y$ का गुणांक धनात्मक हो तो परवलय ऊपर की ओर खुलता है।

(b) $y$ का गुणांक ऋणात्मक हो तो परवलय नीचे की ओर खुलता है।

10.4.2 नाभिलंब जीवा (Latus rectum)

परिभाषा 3 परवलय की नाभि से जाने वाली और परवलय की अक्ष के लंबवत रेखाखंड जिसके अंत्य बिंदु परवलय पर हों, को परवलय की नाभिलंब जीवा कहते हैं (आकृति 10.17)

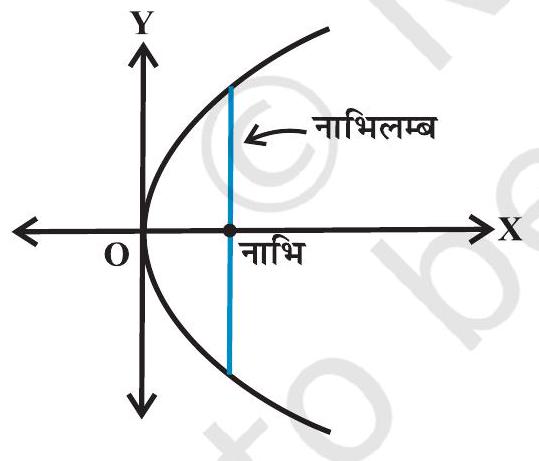
आकृति 10.17

परवलय $y^{2}=4 a x$ की नाभिलंब जीवा की लंबाई ज्ञात करना (आकृति 10.18)

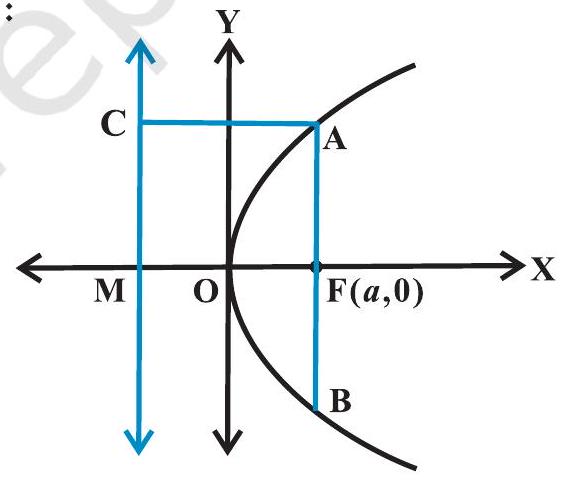
आकृति 10.18

परवलय की परिभाषा के अनुसार, $\mathrm{AF}=\mathrm{AC}$

परंतु $ \mathrm{AC}=\mathrm{FM}=2 a $

अत: $ \mathrm{AF}=2 a $

और क्योंकि परवलय, $x$-अक्ष के परितः सममित है। अतः $\mathrm{AF}=\mathrm{FB}$ और इसलिए

$\mathrm{AB}=$ नाभिलंब जीवा की लंबाई $=4 a$

उदाहरण 5 यदि एक परवलय का समीकरण $y^{2}=8 x$ है तो नाभि के निर्देशांक, अक्ष, नियता का समीकरण और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।

हल दिए समीकरण में $y^{2}$ का पद है इसलिए परवलय $x$-अक्ष के परितः सममित है।

क्योंकि समीकरण में पद $x$ का गुणांक धनात्मक है इसलिए परवलय दाहिनी ओर खुलता है। दिए गए समीकरण $y^{2}=4 a x$, से तुलना करने पर, $a=2$

अतः परवलय की नाभि $(2,0)$ है और परवलय की नियता का समीकरण $x=-2$ है (आकृति 10.19)।

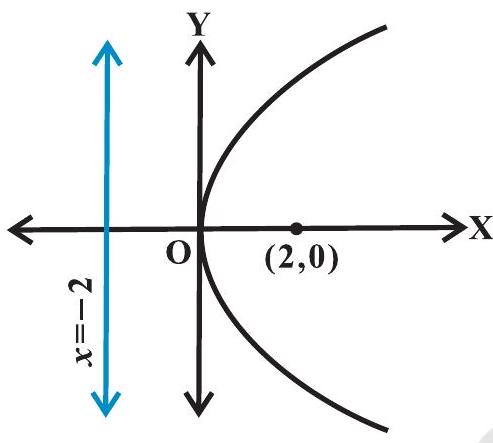
आकृति 10.19

नाभिलंब जीवा की लंबाई $4 a=4 \times 2=8$

उदाहरण 6 नाभि $(2,0)$ और नियता $x=-2$ वाले परवलय का समीकरण ज्ञात कीजिए।

हल क्योंकि नाभि $(2,0) x$-अक्ष पर है इसलिए $x$-अक्ष स्वयं परवलय का अक्ष है। अतः परवलय का समीकरण $y^{2}=4 a x$ या $y^{2}=-4 a x$ के रूप में होना चाहिए क्योंकि नियता $x=-2$ है और नाभि $(2,0)$ है, इसलिए परवलय का समीकरण $y^{2}=4 a x$ के रूप में है जहाँ $a=2$. अत: परवलय का अभीष्ट समीकरण

$y^{2}=4(2) x=8 x$ है।

उदाहरण 7 एक परवलय का समीकरण ज्ञात कीजिए जिसका शीर्ष $(0,0)$ और नाभि $(0,2)$ है।

हल क्योंकि शीर्ष $(0,0)$ पर और नाभि $(0,2)$ पर है, जो $y$-अक्ष पर स्थित है, अतः परवलय का अक्ष, $y$-अक्ष है। इसलिए परवलय का समीकरण, $x^{2}=4 a y$ के रूप में है। अत: परवलय का समीकरण है

$x^{2}=4(2) y$, अर्थात् $x^{2}=8 y$

उदाहरण 8 उस परवलय का समीकरण ज्ञात कीजिए जो $y$-अक्ष के परितः सममित हो और बिंदु $(2,-3)$ से गुज़रता है।

हल क्योंकि परवलय $y$-अक्ष के परितः सममित है और इसका शीर्ष मूल बिंदु पर है, अतः इसका समीकरण $x^{2}=4 a y$ या $x^{2}=-4 a y$, के रूप में है जहाँ चि्न परवलय के ऊपर या नीचे खुलने पर निर्भर करता है परंतु परवलय चतुर्थ चतुर्थांश में स्थित बिंदु $(2,-3)$ से गुज़रता है इसलिए यह अवश्य ही नीचे की ओर खुलेगा। अत: परवलय का समीकरण $x^{2}=-4 a y$ के अनुरूप है, क्योंकि परवलय $(2,-3)$, से गुज़रता है,

अतः हमें प्राप्त होता है,

$ 2^{2}=-4 a(-3), \text { अर्थात् } a=\frac{1}{3} $

अतः परवलय का समीकरण है

$ x^{2}=-4 \frac{1}{3} y, \text { अर्थात् } 3 x^{2}=-4 y $

प्रश्नावली 10.2

निम्नलिखित प्रश्न 1 से 6 तक प्रत्येक में नाभि के निर्देशांक, परवलय का अक्ष, नियता का समीकरण और नाभिलंब जीवा की लंबाई ज्ञात कीजिए:

1. $y^{2}=12 x$

Show Answer

/missing

2. $x^{2}=6 y$

Show Answer

/missing

3. $y^{2}=-8 x$

Show Answer

/missing

4. $x^{2}=-16 y$

Show Answer

/missing

5. $y^{2}=10 x$

Show Answer

6. $x^{2}=-9 y$

Show Answer

/missing

निम्नलिखित प्रश्न 7 से 12 तक प्रत्येक में परवलय का समीकरण ज्ञात कीजिए जो दिए प्रतिबंध को संतुष्ट करता है:

7. Focus $(6,0)$; directrix $x=-6$

Show Answer

/missing

8. Vertex $(0,0)$; focus $(3,0)$

Show Answer

/missing

9. Focus $(0,-3)$; directrix $y=3$

Show Answer

/missing

10. Vertex $(0,0)$; focus $(-2,0)$

Show Answer

/missing

11. Vertex $(0,0)$ passing through $(2,3)$ and axis is along $x$-axis.

Show Answer

/missing

12. Vertex $(0,0)$, passing through $(5,2)$ and symmetric with respect to $y$-axis.

Show Answer

/missing

10.5 दीर्घवृत्त (Ellipse)

परिभाषा 4 एक दीर्घवृत्त तल के उन बिंदुओं का समुच्चय है जिनका तल में दो स्थिर बिंदुओं से दूरी का योग अचर होता है।

दो स्थिर बिंदुओं को दीर्घवृत्त की नाभियाँ कहते हैं (आकृति 10.20)।

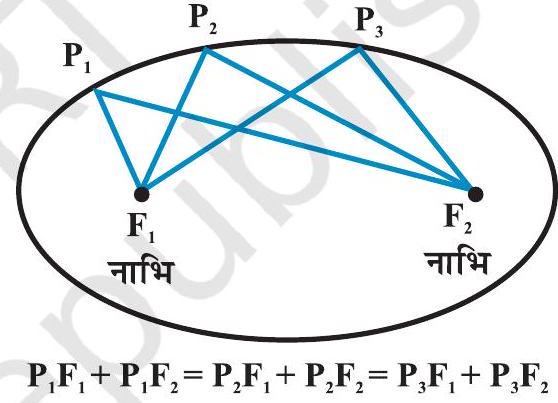
आकृति 10.20

टिप्पणी दीर्घवृत्त पर किसी बिंदु का दो स्थिर बिंदुओं से दूरियों का योग अचर होता है, वह स्थिर बिंदुओं के बीच की दूरी से अधिक होता है।

नाभियों को मिलाने वाले रेखाखंड के मध्य बिंदु को दीर्घवृत्त का केंद्र कहते हैं। दीर्घवृत्त की नाभियों से जाने वाला रेखाखंड, दीर्घवृत्त का दीर्ध अक्ष (Major axis) कहलाता है और केंद्र से जाने वाला और दीर्ध अक्ष पर लंबवत रेखाखंड, दीर्घवृत्त का लघु अक्ष (Minor axis) कहलाता है। र्दीर्घ अक्ष के अन्त्य बिंदुओं को दीर्घवृत्त के शीर्ष कहते हैं (आकृति 10.21)।

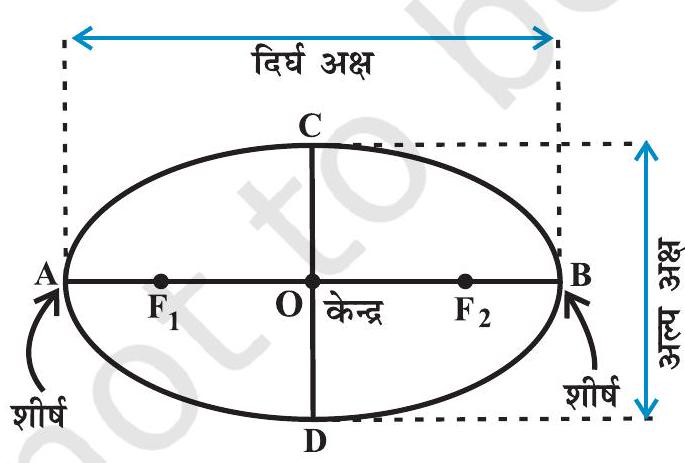
आकृति 10.21

हम दीर्घ अक्ष की लंबाई को, $2 a$ से लघु अक्ष की लंबाई को, $2 b$ से और नाभियों के बीच की दूरी को $2 c$ से लिखते हैं। अतः अर्ध-दीर्घ अक्ष की लंबाई $a$ तथा अर्ध-लघु अक्ष की लंबाई $b$ है ( आकृति 10.22)।

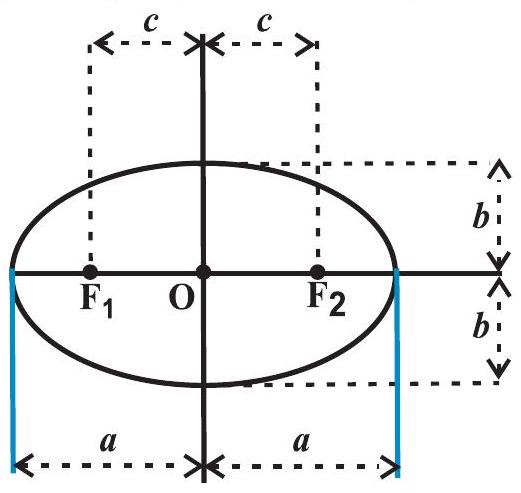
आकृति 10.22

10.5.1 अर्ध-दीर्ध अक्ष, अर्ध-लघु अक्ष और दीर्घवृत्त के केंद्र से नाभि की दूरी के बीच में संबंध (आकृति 10.23)।

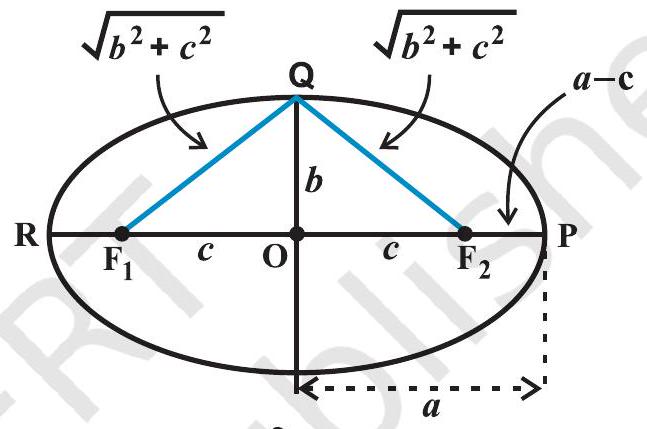
आकृति 10.23

दीर्घवृत्त के दीर्घ अक्ष पर एक अंत्य बिंदु $\mathrm{P}$ लीजिए।

बिंदु $\mathrm{P}$ की नाभियों से दूरियों का योग

$F_1P + F_2P = F_1O + OP + F_2P$

(क्योंकि, $F_1P = F_1O + OP$)

$\quad \quad \quad \quad \quad = c + a +a - c = 2a$

अब लघु अक्ष पर एक अंत्य बिंदु $\mathrm{Q}$ लीजिए।

बिंदु $\mathrm{Q}$ की नाभियों से दूरियों का योग

$$ \mathrm{F} _{1} \mathrm{Q}+\mathrm{F} _{2} \mathrm{Q}=\sqrt{b^{2}+c^{2}}+\sqrt{b^{2}+c^{2}}=2 \sqrt{b^{2}+c^{2}} $$

क्योंकि $\mathrm{P}$ और $\mathrm{Q}$ दोनों दीर्घवृत्त पर स्थित हैं।

अतः दीर्घवृत्त की परिभाषा से हम पाते हैं

$ \begin{aligned} 2 \sqrt{b^{2}+c^{2}} & =2 a, \text{ अर्थात् } \quad a=\sqrt{b^{2}+c^{2}} \\ \text{या} \quad \quad \quad \quad a^{2} & =b^{2}+c^{2}, \text{ अर्थात् } c=\sqrt{a^{2}-b^{2}} \end{aligned} $

10.5.2 उत्केंद्रता (Eccentricity)

परिभाषा 5 दीर्घवृत्त की उत्केंद्रता, दीर्घवृत्त के केंद्र से नाभि और केंद्र से शीर्ष की दूरियों का अनुपात है। उत्केंद्रता को $e$ के द्वारा निर्दिष्ट करते हैं, अर्थात् $e=\frac{c}{a}$ है।

क्योंकि नाभि की केंद्र से दूरी $c$ है इसलिए उत्केंद्रता के पद में नाभि की केंद्र से दूरी $a e$ है।

10.5.3 दीर्घवृत्त का मानक समीकरण (Standard equation of an ellipse)

एक दीर्घवृत्त का समीकरण सरलतम होता है यदि दीर्घवृत्त का केंद्र मूल बिंदु पर हो और नाभियाँ $x$-अक्ष या $y$-अक्ष पर स्थित हों। ऐसे दो संभव दिकविन्यास आकृति 10.24 में दर्शाए गए हैं।

अब हम आकृति 10.24 (a) में दर्शाए गए दीर्घवृत्त, जिसकी नाभियाँ $x$-अक्ष पर स्थित हैं, का समीकरण व्युत्पन्न करेंगें।

मान लीजिए $\mathrm{F} _{1}$ और $\mathrm{F} _{2}$ नाभियाँ हैं और रेखाखंड $\mathrm{F} _{1} \mathrm{~F} _{2}$ का मध्य बिंदु $\mathrm{O}$ है। मान लीजिए $\mathrm{O}$ मूल बिंदु है और $\mathrm{O}$ से $\mathrm{F} _{2}$ की ओर धनात्मक $x$-अक्ष व $\mathrm{O}$ से $\mathrm{F} _{1}$ की ओर ऋणात्मक $x$-अक्ष है। माना $\mathrm{O}$ से $x$-अक्ष पर लंब रेखा $y$-अक्ष है। $\mathrm{F} _{1}$ के निर्देशांक $(-c, 0)$ तथा $\mathrm{F} _{2}$ के निर्देशांक $(c, 0)$ मान लेते हैं (आकृति 10.27)।

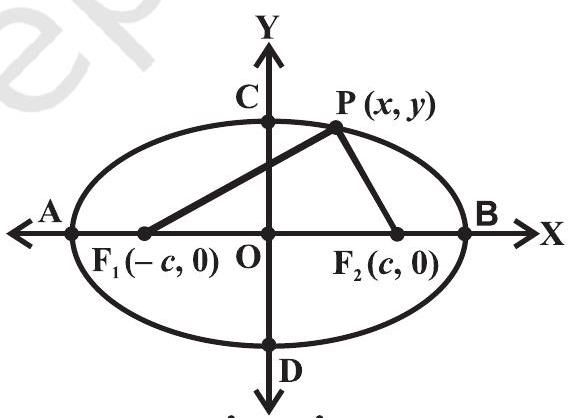
आकृति 10.25

मान लीजिए दीर्घवृत्त पर कोई बिंदु $\mathrm{P}(x, y)$ इस प्रकार है कि $\mathrm{P}$ से दोनों नाभियों की दूरियों का योग $2 a$ है अर्थात्

$ PF_1+PF_2=2 a . \quad \quad \quad \quad \quad \quad \quad \ldots (1) $

दूरी सूत्र से हम पाते हैं,

$ \begin{aligned} & \qquad \sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2 a \\ & \text{ i.e., } \sqrt{(x+c)^{2}+y^{2}}=2 a-\sqrt{(x-c)^{2}+y^{2}} \end{aligned} $

$ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 $

दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं

$ (x+c)^{2}+y^{2}=4 a^{2}-4 a \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2} $

जिसे सरल करने पर मिलता है

$ \sqrt{(x-c)^{2}+y^{2}}=a-\frac{c}{a} x $

पुनः वर्ग करने व सरल करने पर हमें प्राप्त होता है

$ \begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1 & \\ \text{अर्थात्., } \quad \quad\quad \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 & (\text{ क्योंकि } c^{2}=a^{2}-b^{2}) \end{aligned} $

अतः दीर्घवृत्त पर कोई बिंदु

$$ \begin{equation*} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \tag{2} \end{equation*} $$ को संतुष्ट करता है।

विलोमतः माना $\mathrm{P}(x, y)$ समीकरण (2) को संतुष्ट करता है, $0<c<a$. तब

$$ y^{2}=b^{2} \quad 1-\frac{x^{2}}{a^{2}} $$

इसलिए $\mathrm{PF} _{1} \quad=\sqrt{(x+c)^{2}+y^{2}}$

$ =\sqrt{(x+c)^{2}+b^{2} \frac{a^{2}-x^{2}}{a^{2}}} $ $ \begin{aligned} & \left.=\sqrt{(x+c)^{2}+\left(a^{2}-c^{2}\right) \frac{a^{2}-x^{2}}{a^{2}}} \text { (क्योंकि } b^{2}=a^{2}-c^{2}\right) \\ & =\sqrt{a+\frac{c x^{2}}{a}}=a+\frac{c}{a} x \end{aligned} $

इसी प्रकार $ \mathrm{PF} _{2}=a-\frac{c}{a} x $

अत: $ \begin{equation*} \mathrm{PF} _{1}+\mathrm{PF} _{2}=a+\frac{c}{a} x+a-\frac{c}{a} x=2 a \tag{3} \end{equation*} $

इसलिए, कोई बिंदु जो $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, को संतुष्ट करता है, वह ज्यामितीय अनुबंधों को भी संतुष्ट करता है और इसलिए $\mathrm{P}(x, y)$ दीर्घवृत्त पर स्थित है।

इस प्रकार (2) ओर (3) से हमने सिद्ध किया कि एक दीर्घवृत्त, जिसका केंद्र मूल बिंदु और दीर्घ अक्ष $x$-अक्ष के अनुदिश है, का समीकरण

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ है।

विवेचना दीर्घवृत्त के समीकरण से हम यह निष्कर्ष पाते हैं कि दीर्घवृत्त पर प्रत्येक बिंदु $\mathrm{P}(x, y)$ के लिए

$$ \frac{x^{2}}{a^{2}}=1-\frac{y^{2}}{b^{2}} \leq 1 \text {, अर्थात् } x^{2} \leq a^{2} \text {, इसलिए }-a \leq x \leq a \text {. } $$

अतः दीर्घवृत्त रेखाओं $x=-a$ और $x=a$ के बीच में स्थित है और इन रेखाओं को स्पर्श भी करता है।

इसी प्रकार, दीर्घवृत्त, रेखाओं $y=-b$ और $y=b$ के बीच में इन रेखाओं को स्पर्श करता हुआ स्थित है।

इसी प्रकार, हम आकृति 10.24 (b) में, दर्शाए गए दीर्घवृत्त के समीकरण $\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$ को व्युत्पन्न कर सकते हैं। इन दो समीकरणों को दीर्घवृत्त के मानक समीकरण कहते हैं।

टिप्पणी दीर्घवृत्त के मानक समीकरण में, दीर्घवृत्त का केंद्र, मूल बिंदु पर और दीर्घ अक्ष व लघु अक्ष निर्देशांक्षों पर स्थित है। यहाँ ऐसे दीर्घवृत्तों का अध्ययन, जिनका केंद्र कोई अन्य बिंदु हो सकता है और केंद्र से गुज़रने वाली रेखा, दीर्घ अक्ष व लघु अक्ष हो सकते हैं, इस पुस्तक की विषय वस्तु से बाहर हैं।

आकृति 10.24 से प्राप्त दीर्घवृत्त के मानक समीकरण के निरीक्षण से हमें निम्नांकित निष्कर्ष प्राप्त होते हैं।

1. दीर्घवृत्त दोनों निर्देशांक्षों के सापेक्ष सममित है क्योंकि यदि दीर्घवृत्त पर एक बिंदु $(x, y)$ है तो बिंदु $(-x, y),(x,-y)$ और $(-x,-y)$ भी दीर्घवृत्त पर स्थित हैं।

2. दीर्घवृत्त की नाभियाँ सदैव दीर्घ अक्ष पर स्थित होती हैं। दीर्घ अक्ष को सममित रेखा पर अन्त: खंड निकालकर प्राप्त किया जा सकता है। जैसे कि यदि $x^{2}$ का हर बड़ा है तो दीर्ध अक्ष $x$-अक्ष के अनुदिश है और यदि $y^{2}$ का हर बड़ा है तो दीर्घ अक्ष $y$-अक्ष के अनुदिश होता है।

10.5.4 नाभिलंब जीवा (Latus rectum)

परिभाषा 6 दीर्घवृत्त की नाभियों से जाने वाली और दीर्घ अक्ष पर लंबवत रेखाखंड जिसके अंत्य बिंदु दीर्घवृत्त पर हों, को दीर्घवृत्त की नाभिलंब जीवा कहते हैं (आकृति 10.26)।

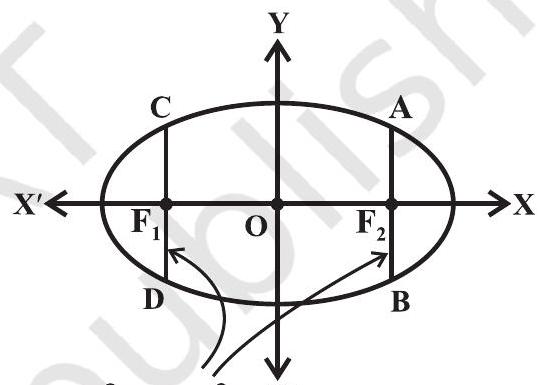
आकृति 10.26

दीर्घवृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ की नाभिलंब जीवा की लंबाई ज्ञात करना

माना $\mathrm{AF} _{2}$ की लंबाई $l$ है

तब $\mathrm{A}$ के निर्देशांक $(c, l)$,अर्थात् $(a e, l)$ है।

क्योंकि $\mathrm{A}$, दीर्घवृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, पर स्थित है। इससे हमें प्राप्त होता है:

$ \begin{aligned} & \frac{(a e)^{2}}{a^{2}}+\frac{l^{2}}{b^{2}}=1 \\ & \Rightarrow l^{2}=b^{2}\left(1-e^{2}\right) \end{aligned} $
परंतु $e^{2}=\frac{c^{2}}{a^{2}}=\frac{a^{2}-b^{2}}{a^{2}}=1-\frac{b^{2}}{a^{2}}$

इसलिए $ l^{2}=\frac{b^{4}}{a^{2}}, \text { अर्थात् } l=\frac{b^{2}}{a} $

क्योंकि दीर्घवृत्त $y$-अक्ष के सापेक्ष सममित होता है, (निःसंदेह यह दोनों अक्षों के सापेक्ष सममित हैं) इसलिए $\mathrm{AF} _{2}=\mathrm{F} _{2} \mathrm{~B}$. अतः नाभिलंब जीवा की लंबाई $\frac{2 b^{2}}{a}$ है।

उदाहरण 9 दीर्घवृत्त $\frac{x^{2}}{25}+\frac{y^{2}}{9}=1$ के नाभियों और शीर्षों के निर्देशांक, दीर्घ एव लघु अक्ष की लंबाइयाँ, उत्केंद्रता और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।

हल क्योंकि $\frac{x^{2}}{25}$ का हर, $\frac{y^{2}}{9}$ के हर से बड़ा है, इसलिए दीर्घ अक्ष $x$-अक्ष के अनुदिश हैं। दिए गए समीकरण की $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$, से तुलना करने पर

$ \begin{gathered} a=5 \text { और } b=3 \text { साथ ही } \\c=\sqrt{a^{2}-b^{2}}=\sqrt{25-9}=4 \end{gathered} $

अतः नाभियों के निर्देशांक $(-4,0)$ और $(4,0)$ है, शीर्षों के निर्देशांक $(-5,0)$ और $(5,0)$ हैं। दीर्घ अक्ष की लंबाई $2 a=10$ इकाइयाँ, लघु अक्ष की लंबाई $2 b=6$ इकाइयाँ और उत्केंद्रता $\frac{4}{5}$ और नाभिलंब $\frac{2 b^{2}}{a}=\frac{18}{5}$ है।

उदाहरण 10 दीर्घवृत्त $9 x^{2}+4 y^{2}=36$ के नाभियों और शीर्षों के निर्देशांक, दीर्घ और लघु अक्ष की लंबाइयाँ, और उत्केंद्रता ज्ञात कीजिए।

हल दिए गए दीर्घवृत्त की समीकरण की प्रमाणिक समीकरण के रूप में लिखने पर

$$ \frac{x^{2}}{4}+\frac{y^{2}}{9}=1 $$

क्योंकि $\frac{y^{2}}{9}$ का हर, $\frac{x^{2}}{4}$ के हर से बड़ा, इसलिए दीर्घ अक्ष, $y$-अक्ष के अनुदिश है । दिए गए समीकरण की मानक समीकरण

$\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$, से तुलना करने पर हमें प्राप्त होता है $b=2$ और $a=3$

$\quad c=\sqrt{a^{2}-b^{2}}=\sqrt{9-4}=\sqrt{5}$

और $\quad e=\frac{c}{a}=\frac{\sqrt{5}}{3}$

अतः नाभियों के निर्देशांक $(0, \sqrt{5})$ व $(0,-\sqrt{5})$, हैं। शीर्षों के निर्देशांक $(0,3)$ व $(0,-3)$ हैं । दीर्घ अक्ष की लंबाई $2 a=6$ इकाइयाँ लघु अक्ष की लंबाई 4 इकाइयाँ और दीर्घवृत्त की उत्केंद्रता $\frac{\sqrt{5}}{3}$ है।

उदाहरण 11 उस दीर्घवृत्त का समीकरण ज्ञात कीजिए, जिसकी नाभियों के निर्देशांक $( \pm 5,0)$ तथा शीर्षों के निर्देशांक $( \pm 13,0)$ हैं।

हल क्योंकि दीर्घवृत्त का शीर्ष $x$-अक्ष पर स्थित है अतः इसका समीकरण

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ के अनुरूप होगा,जहाँ अर्ध-दीर्घ अक्ष की लंबाई $a$ है।

हमें ज्ञात है, कि, $a=13, c= \pm 5$.

अत: $c^{2}=a^{2}-b^{2}$, के सूत्र से हमें प्राप्त होता है,

$25=169-b^{2}$ या $b=12$

अत: दीर्घवृत्त का समीकरण $\frac{x^{2}}{169}+\frac{y^{2}}{144}=1$ है।

उदाहरण 12 उस दीर्घवृत्त का समीकरण ज्ञात कीजिए, जिसके दीर्घ अक्ष की लंबाई 20 है तथा नाभियाँ $(0, \pm 5)$ हैं।

हल क्योंकि नाभियाँ $y$-अक्ष पर स्थित हैं, इसलिए दीर्घवृत्त का समीकरण $\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$ के अनुरूप है।

दिया है $ a=\text { अर्ध दीर्घ अक्ष }=\frac{20}{2}=10 $

और सूत्र

$ \begin{aligned} & c^{2}=a^{2}-b^{2} \text { से प्राप्त होता है, } \\ & 5^{2}=10^{2}-b^{2} \text { या } b^{2}=75 \end{aligned} $

अत:

$ \frac{x^{2}}{75}+\frac{y^{2}}{100}=1 $

उदाहरण 13 उस दीर्घवृत्त का समीकरण ज्ञात कीजिए, जिसकी दीर्घ अक्ष, $x$-अक्ष के अनुदिश है और $(4,3)$ तथा $(-1,4)$ दीर्घवृत्त पर स्थित हैं।

हल दीर्घवृत्त के समीकरण का मानक रूप $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ है। चूँकि बिंदु $(4,3)$ तथा $(-1,4)$ दीर्घवृत्त पर स्थित हैं। अतः हमें प्राप्त होता है,

$ \begin{align*} & \frac{16}{a^{2}}+\frac{9}{b^{2}}=1 \tag{1}\\ & \frac{1}{a^{2}}+\frac{16}{b^{2}}=1 \tag{2} \end{align*} $

समीकरण (1) और (2) को हल करने पर $a^{2}=\frac{247}{7}$ व $b^{2}=\frac{247}{15}$ प्राप्त होता है।

अतः अभीष्ट समीकरण:

$ \frac{x^{2}}{\frac{247}{7}}+\frac{y^{2}}{\frac{247}{15}}=1 \text { या } 7 x^{2}+15 y^{2}=247 \text { है। } $

प्रश्नावली 10.3

निम्नलिखित प्रश्नों 1 से 9 तक प्रत्येक दीर्घवृत्त में नाभियों और शीर्षों के निर्देशांक, दीर्घ और लघु अक्ष की लंबाइयाँ, उत्केंद्रता तथा नाभिलंब जीवा की लंबाई ज्ञात कीजिए:

1. $\frac{x^{2}}{36}+\frac{y^{2}}{16}=1$

Show Answer

\missing

2. $\frac{x^{2}}{4}+\frac{y^{2}}{25}=1$

Show Answer

/missing

3. $\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$

Show Answer

/missing

4. $\frac{x^{2}}{25}+\frac{y^{2}}{100}=1$

Show Answer

/missing

5. $\frac{x^{2}}{49}+\frac{y^{2}}{36}=1$

Show Answer

/missing

6. $\frac{x^{2}}{100}+\frac{y^{2}}{400}=1$

Show Answer

/missing

7. $36 x^{2}+4 y^{2}=144$

Show Answer

/missing

8. $16 x^{2}+y^{2}=16$

Show Answer

/missing

9. $4 x^{2}+9 y^{2}=36$

Show Answer

/missing

निम्नलिखित प्रश्नों 10 से 20 तक प्रत्येक में, दिए प्रतिबंधों को संतुष्ट करते हुए दीर्घवृत्त का समीकरण ज्ञात कीजिए:

10. शीर्षों $( \pm 5,0)$, नाभियाँ $( \pm 4,0)$

Show Answer

/missing

11. शीर्षों $(0, \pm 13)$, नाभियाँ $(0, \pm 5)$

Show Answer

/missing

12. शीर्षों $( \pm 6,0)$, नाभियाँ $( \pm 4,0)$

Show Answer

/missing

13. दीर्घ अक्ष के अंत्य बिंदु $( \pm 3,0)$, लघु अक्ष के अंत्य बिंदु $(0, \pm 2)$

Show Answer

/missing

14. दीर्घ अक्ष के अंत्य बिंदु $(0, \pm \sqrt{5})$, लघु अक्ष के अंत्य बिंदु $( \pm 1,0)$

Show Answer

/missing

15. दीर्घ अक्ष की लंबाई 26 , नाभियाँ $( \pm 5,0)$

Show Answer

/missing

16. दीर्घ अक्ष की लंबाई 16 , नाभियाँ $(0, \pm 6)$.

Show Answer

/missing

17. नाभियाँ $( \pm 3,0), a=4$

Show Answer

/missing

18. $b=3, c=4$, केंद्र मूल बिंदु पर, नाभियाँ $x$ अक्ष पर

Show Answer

/missing

19. केंद्र $(0,0)$ पर, दीर्घ-अक्ष, $y$-अक्ष पर और बिंदुओं $(3,2)$ और $(1,6)$ से जाता है।

Show Answer

/missing

20. दीर्घ अक्ष, $x$-अक्ष पर और बिंदुओं $(4,3)$ और $(6,2)$ से जाता है।

Show Answer

/missing

10.6 अतिपरवलय (Hyperbola)

परिभाषा 7 एक अतिपरवलय, तल के उन सभी बिंदुओं का समुच्चय है जिनकी तल में दो स्थिर बिंदुओं से दूरी का अंतर अचर होता है।

परिभाषा में ‘अंतर’ शब्द का प्रयोग किया गया है जिसका अर्थ है दूर स्थित बिंदु से दूरी ऋण निकट स्थित बिंदु से दूरी। दो स्थिर बिंदुओं को दीर्घवृत्त की नाभियाँ कहते हैं। नाभियों को मिलाने वाले रेखाखंड के मध्य बिंदु को अतिपरवलय का केंद्र कहते हैं। नाभियों से गुज़रने वाली रेखा को अनुप्रस्थ अक्ष (transverse axis) तथा केंद्र से गुज़रने वाली रेखा और अनुप्रस्थ अक्ष पर लंबवत् रेखा को संयुग्मी अक्ष (conjugate axis) कहते हैं। अतिपरवलय, अनुप्रस्थ अक्ष को जिन बिंदुओं पर काटता है, उन्हें अतिपरवलय के शीर्ष (vertices) कहते हैं (आकृति 10.27)।

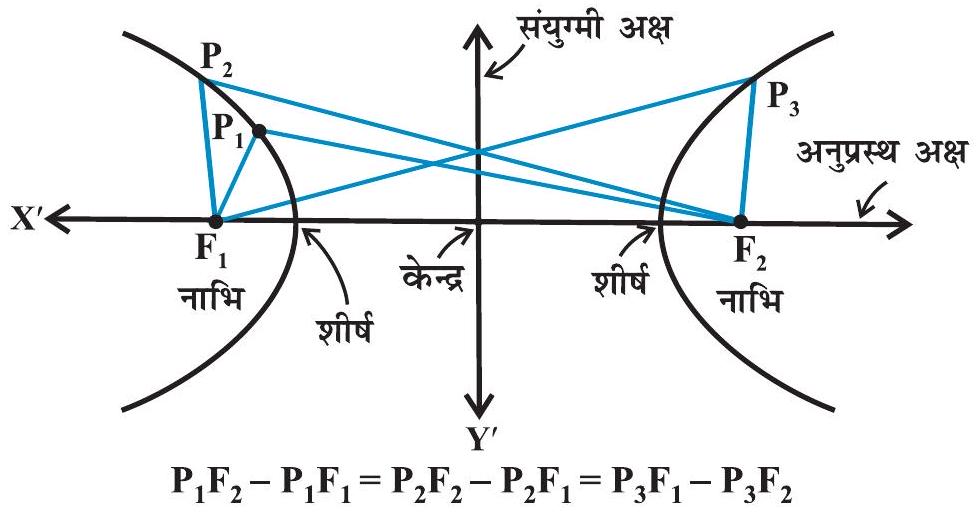
आकृति 10.27

दोनों नाभियों के बीच की दूरी को हम $2 c$ से प्रदर्शित करते हैं, दोनों शीर्षों के बीच की दूरी (अनुप्रस्थ अक्ष की लंबाई) को $2 a$ से प्रदर्शित करते हैं और हम राशि $b$ को इस प्रकार परिभाषित करते हैं कि

$b=\sqrt{c^{2}-a^{2}} $

$2 b$ को संयुग्मी अक्ष की लंबाई भी कहते है (आकृति 10.28)।

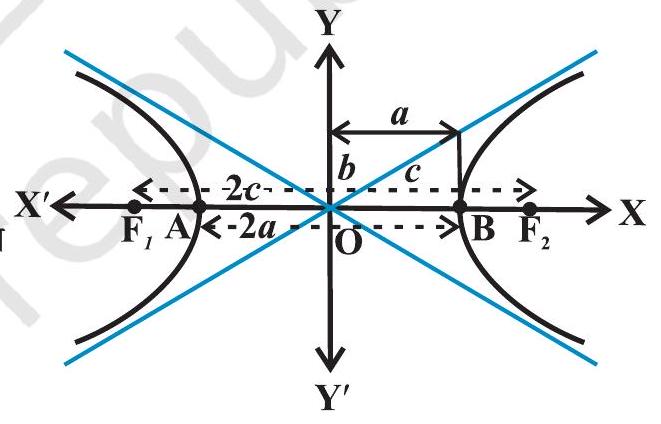
आकृति 10.28

समीकरण (1) की अचर राशि $\mathbf{P} _{1} \mathbf{F} _{2}-\mathbf{P} _{1} \mathbf{F} _{1}$ ज्ञात करना

आकृति 11.30 में $\mathrm{A}$ तथा $\mathrm{B}$ पर बिंदु $\mathrm{P}$ को रखने पर हमें प्राप्त होता है,

$\mathrm{BF} _{1}-\mathrm{BF} _{2}=\mathrm{AF} _{2}-\mathrm{AF} _{1}$ (अतिपरवलय की परिभाषा के अनुसार)

$\mathrm{BA}+\mathrm{AF} _{1}-\mathrm{BF} _{2}=\mathrm{AB}+\mathrm{BF} _{2}-\mathrm{AF} _{1}$

अर्थात् $\mathrm{AF} _{1}=\mathrm{BF} _{2}$

इसलिए, $\mathrm{BF} _{1}-\mathrm{BF} _{2}=\mathrm{BA}+\mathrm{AF} _{1}-\mathrm{BF} _{2}=\mathrm{BA}=2 a$

10.6.1 उत्केंद्रता (Eccentricity)

परिभाषा 8 दीर्घवृत्त की तरह ही अनुपात $e=\frac{c}{a}$ को अतिपरवलय की उत्केंद्रता कहते हैं। चूँकि $c \geq a$, इसलिए उत्केंद्रता कभी भी एक से कम नहीं होती है। उत्केंद्रता के संबंध में, नाभियाँ केंद्र से $a e$ की दूरी पर होती है।

10.6.2 अतिपरवलय का मानक समीकरण (Standard equation of Hyperbola)

यदि अतिपरवलय का केंद्र मूल बिंदु पर और नाभियाँ $x$-अक्ष और $y$-अक्ष पर स्थित हों तो अतिपरवलय का समीकरण सरलतम होता है ऐसे दो संभव दिक्विन्यास आकृति 10.29 में दर्शाए गए हैं।

अब हम आकृति 10.29(a) में दर्शाए गए अतिपरिवलय, जिसकी नाभियाँ $x$-अक्ष पर स्थित हैं का समीकरण व्युत्पन्न करेंगे।

मान लीजिए $\mathrm{F} _{1}$ और $\mathrm{F} _{2}$ नाभियाँ हैं और रेखाखंड $\mathrm{F} _{1} \mathrm{~F} _{2}$ का मध्य बिंदु $\mathrm{O}$ है। मान लीजिए $\mathrm{O}$ मूल बिंदु है और $\mathrm{O}$ से $\mathrm{F} _{2}$ की ओर धनात्मक $x$-अक्ष व $\mathrm{O}$ से $\mathrm{F} _{1}$ की ओर ऋणात्मक $x$-अक्ष है। माना $\mathrm{O}$ से $x$-अक्ष पर लंब $y$-अक्ष है। $\mathrm{F} _{1}$ के निर्देशांक $(-c, 0)$ और $\mathrm{F} _{2}$ के निर्देशांक $(c, 0)$ मान लेते हैं (आकृति 10.30)।

आकृति 10.30

मान लीजिए अतिपरवलय पर कोई बिंदु $\mathrm{P}(x, y)$ इस प्रकार है कि $\mathrm{P}$ की दूरस्थ बिंदु से व निकटस्थ बिंदु से दूरीयों का अंतर $2 a$ है इसलिए, $\mathrm{PF} _{1}-\mathrm{PF} _{2}=2 a$

दूरी सूत्र से हम पाते हैं

$ \begin{aligned} & \quad \quad \quad \quad \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}=2 a \\ &\text{अतः, } \quad \quad \quad \sqrt{(x+c)^{2}+y^{2}}=2 a+\sqrt{(x-c)^{2}+y^{2}} \end{aligned} $

दोनों पक्षों का वर्ग करने पर, हम प्राप्त करते हैं,

$ (x+c)^{2}+y^{2}=4 a^{2}+4 a \quad \sqrt{(x-c)^{2}+y^{2}}+(x-c)^{2}+y^{2} $

जिसे सरल करने पर मिलता है

$ \frac{c x}{a}-a=\sqrt{(x-c)^{2}+y^{2}} $

पुन: वर्ग करने व सरल करने पर हमें प्राप्त होता है,

$ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{c^{2}-a^{2}}=1 $

अतः, $\quad \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad$ (Since $c^{2}-a^{2}=b^{2}$ )

अतः अप्रतिपरवलय पर स्थित कोई बिंदु $ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 $ को संतुष्ट करता है।

विलोमतः माना $\mathrm{P}(x, y)$, समीकरण (3) को संतुष्ट करता है, $0<a<c$. तब,

$ y^{2}=b^{2}(\frac{x^{2}-a^{2}}{a^{2}}) $

इस प्रकार

$ \begin{aligned} PF_1 & =+\sqrt{(x+c)^{2}+y^{2}} \\ & =+\sqrt{(x+c)^{2}+b^{2}(\frac{x^{2}-a^{2}}{a^{2}})}=a+\frac{c}{a} x \end{aligned} $

इसी प्रकार $ \mathrm{PF} _{2}=a-\frac{a}{c} x $

अतिपरवलय में $c>a$ और चूँकि $\mathrm{P}$ रेखा $x=a$, के दाहिनी ओर है, $x>a$, और इसलिए $\frac{c}{a} x>a$.

या $a-\frac{c}{a} x$ ॠणात्मक हो जाता है। अत: $\mathrm{PF} _{2}=\frac{c}{a} x-a$.

इसलिए $\mathrm{PF} _{1}-\mathrm{PF} _{2}=a+\frac{c}{a} x-\frac{c x}{a}+a=2 a$

ध्यान दीजिए, यदि $\mathrm{P}$ रेखा $x=-a$, के बाईं ओर होता तब

$\mathrm{PF} _{1}=-\left(a+\frac{c}{a} x\right), \mathrm{PF} _{2}=a-\frac{c}{a} x$.

उस स्थिति में $\mathrm{PF} _{2}-\mathrm{PF} _{1}=2 a$. इसलिए कोई बिंदु जो $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, को संतुष्ट करता है तो अतिपरवलय पर स्थित होता है।

इस प्रकार हमने सिद्ध किया कि एक अतिपरवलय, जिसका केंद्र $(0,0)$ व अनुप्रस्थ अक्ष, $x$-अक्ष के अनुदिश है, का समीकरण है $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$.

टिप्पणी एक अतिपरवलय जिसमें $a=b$ हो, समकोणीय अतिपरवलय (rectangular hyperbola) कहलाता है।

विवेचना अतिपरवलय के समीकरण से हम यह निष्कर्ष पाते हैं कि अतिपरवलय पर प्रत्येक बिंदु $(x, y)$ के लिए, $\frac{x^{2}}{a^{2}}=1+\frac{y^{2}}{b^{2}} \geq 1$.

अर्थात् $\left|\frac{x}{a}\right| \geq 1$, अर्थात् $x \leq-a$ या $x \geq a$. इसलिए, वक्र का भाग रेखाओं $x=+a$ और $x=-a$, के बीच में स्थित नहीं है (अथवा संयुग्मी अक्ष पर वास्तविक अंतःखंड नहीं होते हैं)।

इसी प्रकार, आकृति 10.29 (b) में, हम अतिपरवलय का समीकरण $\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1$ व्युत्पन्न कर सकते हैं। इन दो समीकरणों को अतिपरवलय का मानक समीकरण कहते हैं।

टिप्पणी अतिपरवलय के मानक समीकरण में, अतिपरवलय का केंद्र, मूल बिंदु पर और अनुप्रस्थ अक्ष व संयुग्मी अक्ष निर्देशांक्षो पर स्थित हैं। तथापि यहाँ ऐसे भी अतिपरवलय होते हैं जिनमें कोई दो लंबवत् रेखाएँ अनुप्रस्थ अक्ष व संयुग्मी अक्ष होते हैं परंतु ऐसी स्थितियों का अध्ययन उच्च कक्षाओं में हैं।

आकृति 10.27 , से प्राप्त अतिपरवलयों के मानक समीकरण के निरीक्षण से हमें निम्नलिखित निष्कर्ष प्राप्त होते हैं:

1. अतिपरवलय, दोनों निर्देशांक्षों के सापेक्ष सममित हैं क्योंकि यदि अतिपरवलय पर एक बिंदु $(x, y)$ है तो बिंदु $(-x, y),(x,-y)$ और $(-x,-y)$ भी अतिपरवलय पर स्थित हैं।

2. अतिपरवलय की नाभियाँ सदैव अनुप्रस्थ अक्ष पर स्थित होती हैं। यह सदैव एक धनात्मक पद है जिसका हर अनुप्रस्थ अक्ष देता है। उदाहरणतः $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$ का अनुप्रस्थ अक्ष, $x$-अक्ष के अनुदिश है और इसकी लंबाई 6 है जबकि $\frac{y^{2}}{25}-\frac{x^{2}}{16}=1$ का अनुप्रस्थ अक्ष, $y$-अक्ष के अनुदिश है और इसकी लंबाई 10 है।

10.6.3 नाभिलंब जीवा (Latus rectum)

परिभाषा 9 अतिपरवलय की नाभियों से जाने वाली और अनुप्रस्थ अक्ष पर लंबवत् रेखाखंड जिसके अंत्य बिंदु अतिपरवलय पर हों, को अतिपरवलय की नाभिलंब जीवा कहते हैं।

दीर्घवृत्तों की भाँति, यह दर्शाना सरल है कि अतिपरवलय की नाभिलंब जीवा की लंबाई $\frac{2 b^{2}}{a}$ है।

उदाहरण 14 निम्नलिखित अतिपरवलयों के शीर्षों और नाभियों के निर्देशांकों, उत्केंद्रता और नाभिलंब जीवा की लंबाई ज्ञात कीजिए।

(i) $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$ (ii) $y^{2}-16 x^{2}=16$

हल (i) दिए गए समीकरण $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$ का मानक समीकरण

$$ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \text { से तुलना करने पर, हम पाते हैं कि } $$

$a=3, b=4$ और $c=\sqrt{a^{2}+b^{2}}=\sqrt{9+16}=5$

अतः नाभियों के निर्देशांक $( \pm 5,0)$ हैं और शीर्षों के निर्देशांक $( \pm 3,0)$ हैं।

उत्केंद्रता $e=\frac{c}{a}=\frac{5}{3}$ नाभिलंब जीवा की लंबाई $=\frac{2 b^{2}}{a}=\frac{32}{3}$

(ii) दिये गए समीकरण के दोनों पक्षों को 16 से भाग करने पर $\frac{y^{2}}{16}-\frac{x^{2}}{1}=1$

हमें प्राप्त होता है, मानक समीकरण $\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1$, से तुलना करने पर हम पाते हैं कि $a=4, b=1$ और $c=\sqrt{a^{2}+b^{2}}=\sqrt{16+1}=\sqrt{17}$

अतः नाभियों के निर्देशांक $(0, \pm \sqrt{17})$ हैं और शीर्षों के निर्देशांक $(0, \pm 4)$ हैं।

उत्केंद्रता $e=\frac{c}{a}=\frac{\sqrt{17}}{4}$ नाभिलंब जीवा की लंबाई $=\frac{2 b^{2}}{a}=\frac{1}{2}$.

उदाहरण 15 नाभियाँ $(0, \pm 3)$ और शीर्षों $\left(0, \pm \frac{\sqrt{11}}{2}\right)$ वाले अतिपरवलय का समीकरण ज्ञात कीजिए।

हल क्योंकि नाभियाँ $y$-अक्ष पर हैं, इसलिए अतिपरवलय का समीकरण $\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1$ के रूप में है।

क्योंकि शीर्ष $\left(0, \pm \frac{\sqrt{11}}{2}\right)$, इसलिए $a=\frac{\sqrt{11}}{2}$

और नाभियाँ $(0, \pm 3) ; c=3$ और $b^{2}=c^{2}-a^{2}=\frac{25}{4}$.

इसलिए, अतिपरवलय का समीकरण है

$ \frac{y^{2}}{\left(\frac{11}{4}\right)}-\frac{x^{2}}{\left(\frac{25}{4}\right)}=1, \text { अर्थात् } 100 y^{2}-44 x^{2}=275 $

उदाहरण 16 उस अतिपरवलय का समीकरण ज्ञात कीजिए जिसकी नाभियाँ $(0, \pm 12)$ और नाभिलंब जीवा की लंबाई 36 है।

हल क्योंकि नाभियाँ $(0, \pm 12)$, है इसलिए $c=12$.

नाभिलंब जीवा की लंबाई $=\frac{2 b^{2}}{a}=36, b^{2}=18 a$

$ \begin{aligned} & \text{इसलिए} \quad \quad\quad\quad c^{2}=a^{2}+b^{2} ; \text{ gives } \\ & \quad\quad\quad\quad\quad\quad\quad\quad\quad 144=a^{2}+18 a \\ & \text{ अर्थात् } \quad\quad\quad\quad\quad\quad\quad a^{2}+18 a-144=0, \\ & \text{ } \quad \quad\quad\quad\quad\quad\quad a=-24,6 . \end{aligned} $

क्योंकि $a$ ॠणात्मक नहीं हो सकता है, इसलिए हम $a=6$ लेते हैं और $b^{2}=108$.

अतः अभीष्ट अतिपरवलय का समीकरण $\frac{y^{2}}{36}-\frac{x^{2}}{108}=1$ है, अर्थात् $3 y^{2}-x^{2}=108$

प्रश्नावली 10.4

निम्नलिखित प्रश्न 1 से 6 तक प्रत्येक में, अतिपरवलयों के शीर्षों, नाभियों के निर्देशांक, उत्केंद्रता और नाभिलंब जीवा की लंबाई ज्ञात कीजिए:

1. $\frac{x^{2}}{16}-\frac{y^{2}}{9}=1$

Show Answer

\missing

2. $\frac{y^{2}}{9}-\frac{x^{2}}{27}=1$

Show Answer

/missing

3. $9 y^{2}-4 x^{2}=36$

Show Answer

\missing

4. $16 x^{2}-9 y^{2}=576$

Show Answer

/missing

5. $5 y^{2}-9 x^{2}=36$

Show Answer

/missing

6. $49 y^{2}-16 x^{2}=784$.

Show Answer

/missing

निम्नलिखित प्रश्न 7 से 15 तक प्रत्येक में, दिए गए प्रतिबंधों को संतुष्ट करते हुए अतिपरवलय का समीकरण ज्ञात कीजिए:

7. शीर्ष $( \pm 2,0)$, नाभियाँ $( \pm 3,0)$

Show Answer

\missing

8. शीर्ष $(0, \pm 5)$, नाभियाँ $(0, \pm 8)$

Show Answer

\missing

9. शीर्ष $(0, \pm 3)$, नाभियाँ $(0, \pm 5)$

Show Answer

\missing

10. नाभियाँ $( \pm 5,0)$, अनुप्रस्थ अक्ष की लंबाई 8 है।

Show Answer

\missing

11. नाभियाँ $(0, \pm 3)$, संयुग्मी अक्ष की लंबाई 24 है।.

Show Answer

\missing

12. नाभियाँ $( \pm 3 \sqrt{5}, 0)$, नाभिलंब जीवा की लंबाई 8 है।

Show Answer

/missing

13. नाभियाँ $( \pm 4,0)$, नाभिलंब जीवा की लंबाई 12 है।

Show Answer

\missing

14. शीर्ष $( \pm 7,0), e=\frac{4}{3}$.

Show Answer

\missing

15. नाभियाँ $(0, \pm \sqrt{10})$, हैं तथा $(2,3)$ से होकर जाता है।

Show Answer

\missing

विविध उदाहरण

उदाहरण 17 एक परवलयाकार परावर्तक की नाभि, इसके शीर्ष केंद्र से 5 सेमी की दूरी पर है जैसा कि आकृति 10.31 में दर्शाया गया है। यदि परावर्तक 45 सेमी गहरा है, तो आकृति 10.31 में दूरी $\mathrm{AB}$ ज्ञात कीजिए (आकृति 10.31)।

आकृति 10.31

हल क्योंकि नाभि की केंद्र शीर्ष से दूरी 5 सेमी है, हम $a=5$ सेमी पाते हैं। यदि शीर्ष मूल बिंदु और दर्पण की अक्ष, $x$-अक्ष के धन भाग के अनुदिश हो तो परवलयाकार परिच्छेद का समीकरण

$ \quad\quad\quad\quad\quad\quad\quad\quad\quad y^{2}=4(5) x=20 x $

यदि $ \quad\quad\quad\quad\quad x=45 . \text{ तो हम पाते हैं } $

$ \quad\quad\quad\quad\quad\quad\quad\quad\quad y^{2}=900 $

इसलिए $ \quad\quad\quad\quad\quad\quad y= \pm 30 $

अतः $\quad\quad\quad\quad\quad\quad AB = 2y = 2 \times 30 = 60 \text{cm} $.

उदाहरण 18 एक दंड के सिरे, 12 मीटर दूर रखे आधारों पर टिके हैं। चूँकि दंड का भार केंद्र पर केंद्रित होने से दंड में केंद्र पर 3 सेमी का झुकाव आ जाता है और झुका हुआ दंड एक परवलयाकार है। केंद्र से कितनी दूरी पर झुकाव 1 सेमी है?

हल मान लीजिए शीर्ष निम्नतम बिंदु पर और अक्ष उर्ध्वाधर है। माना निर्देशांक्ष, आकृति 10.32 के अनुसार दर्शाए गए हैं।

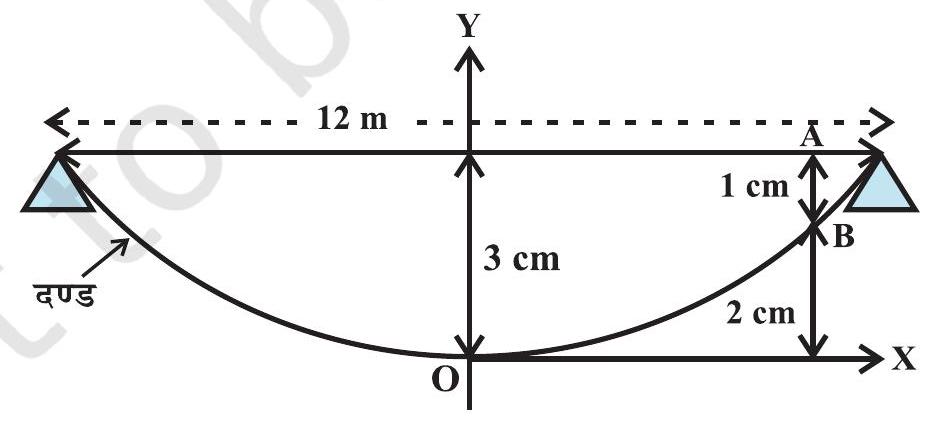
आकृति 10.32

परवलय का समीकरण $x^{2}=4 a y$ जैसा है। चूँकि यह $6, \frac{3}{100}$, से गुज़रता है इसलिए हमें $(6)^{2}=4 a \frac{3}{100}$, अर्थात् $a=\frac{36 \times 100}{12}=300$ मी प्राप्त है।

अब दंड में झुकाव $\mathrm{AB}, \frac{1}{100}$ मी है। $\mathrm{B}$ के निर्देशांक $\left(x, \frac{2}{100}\right)$ हैं।

$ \begin{aligned} \text{इसलिए } \quad\quad\quad\quad\quad x^{2} & =4 \times 300 \times \frac{2}{100}=24 \\ \text{i.e. }\quad\quad\quad\quad\quad x & =\sqrt{24} \quad=2 \sqrt{6} \text{ मी } \end{aligned} $

उदाहरण 19 15 सेमी लंबी एक छड़ $\mathrm{AB}$ दोनों निर्देशांक्षों के बीच में इस प्रकार रखी गई है कि उसका एक सिरा $\mathrm{A}, x$-अक्ष पर और दूसरा सिरा $\mathrm{B}, y$-अक्ष पर रहता है छड़ पर एक बिंदु $\mathrm{P}(x, y)$ इस प्रकार लिया गया है कि $\mathrm{AP}=6$ सेमी हैं दिखाइए कि $\mathrm{P}$ का बिंदुपथ एक दीर्घवृत्त है।

हल मान लीजिए छड़ $\mathrm{AB}, \mathrm{OX}$ के साथ $\theta$ कोण बनाती है जैसा कि आकृति 10.33 में दिखाया गया है। $\mathrm{AB}$ पर बिंदु $\mathrm{P}(x, y)$ इस प्रकार है कि $\mathrm{AP}=6$ सेमी है।

आकृति 10.33

$ \begin{aligned} & \text {क्योंकि } \quad \quad \quad\quad AB=15 \text{ सेमी, इसलिए } \\ & \quad\quad\quad \quad\quad\quad \quad PB=9 \text{ सेमी.} \end{aligned} $

$\mathrm{P}$ से $\mathrm{PQ}$ और $\mathrm{PR}$ क्रमशः $y$-अक्ष और $x$-अक्ष पर लंब डालिए।

से $\quad\quad\quad \quad \Delta PBQ, \cos \theta=\frac{x}{9}$

से $ \quad\quad\quad \quad \Delta PRA, \sin \theta=\frac{y}{6} $

क्योंकि $\cos ^{2} \theta+\sin ^{2} \theta=1$

अतः $ \frac{x}{9}^{2}+\frac{y}{6}^{2}=1 $

या $ \quad\quad\quad \quad \frac{x^{2}}{81}+\frac{y^{2}}{36}=1 $

अतः $\mathrm{P}$ का बिंदुपथ एक दीर्घवृत्त है।

अध्याय 10 पर आधारित विविध प्रश्नावली

1. यदि एक परवलयाकार परावर्तक का व्यास 20 सेमी और गहराई 5 सेमी है। नाभि ज्ञात कीजिए।

Show Answer

/missing

2. एक मेहराब परवलय के आकार का है और इसका अक्ष ऊर्ध्वाधर है। मेहराव 10 मीटर ऊँचा है और आधार में 5 मीटर चौड़ा है यह, परवलय के दो मीटर की दूरी पर शीर्ष से कितना चौड़ा होगा?

Show Answer

/missing

3. एक सर्वसम भारी झूलते पुल की केबिल (cable)परवलय के रूप में लटकी हुई है। सड़क पथ जो क्षैतिज है 100 मीटर लंबा है तथा केबिल से जुड़े ऊर्ध्वाधर तारों पर टिका हुआ है, जिसमें सबसे लंबा तार 30 मीटर और सबसे छोटा तार 6 मीटर है। मध्य से 18 मीटर दूर सड़क पथ से जुड़े समर्थक (supporting) तार की लंबाई ज्ञात कीजिए।

Show Answer

/missing

4. एक मेहराव अर्ध-दीर्घवृत्ताकार रूप का है। यह 8 मीटर चौड़ा और केंद्र से 2 मीटर ऊँचा है। एक सिरे से 1.5 मीटर दूर बिंदु पर मेहराव की ऊँचाई ज्ञात कीजिए।

Show Answer

/missing

5. एक 12 सेमी लंबी छड़ इस प्रकार चलती है कि इसके सिरे निर्देशांक्षो को स्पर्श करते हैं। छड़ के बिंदु $\mathrm{P}$ का बिंदुपथ ज्ञात कीजिए जो $x$-अक्ष के संपर्क वाले सिरे से 3 सेमी दूर है।

Show Answer

/missing

6. त्रिभुज का क्षेत्रफल ज्ञात कीजिए जो परवलय $x^{2}=12 y$ के शीर्ष को इसकी नाभिलंब जीवा के सिरों को मिलाने वाली रेखाओं से बना है।

Show Answer

/missing

7. एक व्यक्ति दौड़पथ पर दौड़ते हुऐ अंकित करता है कि उससे दो झंडा चौकियों की दूरियों का योग सदैव 10 मीटर रहता है। और झंडा चौकियों के बीच की दूरी 8 मीटर है। व्यक्ति द्वारा बनाए पथ का समीकरण ज्ञात कीजिए।

Show Answer

/missing

8. परवलय $y^{2}=4 a x$, के अंतर्गत एक समबाहु त्रिभुज है जिसका एक शीर्ष परवलय का शीर्ष है। त्रिभुज की भुजा की लंबाई ज्ञात कीजिए।

Show Answer

/missing

सारांश

इस अध्याय में निम्नलिखित संकल्पनाओं एवं व्यापकताओं का अध्ययन किया है।

एक वृत्त, तल के उन बिंदुओं का समुच्चय है जो तल के एक स्थिर बिंदु से समान दूरी पर होते हैं।

केंद्र $(h, k)$ तथा त्रिज्या $r$ के वृत्त का समीकरण

$(x-h)^{2}+(y-k)^{2}=r^{2}$ है।

एक परवलय तल के उन सभी बिंदुओं का समुच्चय है जो एक निश्चित सरल रेखा और तल के एक निश्चित बिंदु से समान दूरी पर हैं।

नाभि $(a, 0), a>0$ और नियता $x=-a$ वाले परवलय का समीकरण

$y^{2}=4 a x$ है।

परवलय की नाभि से जाने वाली और परवलय के अक्ष के लंबवत रेखाखंड जिसके अंत्य बिंदु परवलय पर हों, को परवलय की नाभिलंब जीवा कहते हैं।

परवलय $y^{2}=4 a x$ के नाभिलंब जीवा की लंबाई $4 a$ है।

एक दीर्घवृत्त तल के उन बिंदुओं का समुच्चय है जिनकी तल में दो स्थिर बिंदुओं से दूरी का योग अचर होता है।

$x$-अक्ष पर नाभि वाले दीर्घवृत्त का समीकरण $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ है।

दीर्घवृत्त की किसी भी नाभि से जाने वाली और दीर्घ अक्ष पर लंबवत रेखाखंड, जिसके अंत्य बिंदु दीर्घवृत्त पर हों, को दीर्घवृत्त की नाभिलंब जीवा कहते हैं।

दीर्घवृत्त $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ के नाभिलंब जीवा की लंबाई $\frac{2 b^{2}}{a}$ है।

दीर्घवृत्त की उत्केंद्रता, दीघर्वृत्त के केंद्र से नाभि और केंद्र से शीर्ष की दूरियों का अनुपात है।

एक अतिपरवलय तल के उन सभी बिंदुओं का समुच्चय है जिनकी तल में दो स्थिर बिंदुओं से दूरी का अंतर अचर होता है।

$x$-अक्ष पर नाभि वाले अतिपरवलय का समीकरण $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ है।

अतिपरिवलय की किसी भी नाभि से जाने वाली और अनुप्रस्थ पर लंबवत रेखाखंड जिसके अंत्य बिंदु अतिपरवलय पर हों, को अतिपरवलय की नाभिलंब जीवा कहते हैं।

अतिपरवलय $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ के नाभिलंब जीवा की लंबाई $\frac{2 b^{2}}{a}$ है।

अतिपरवलय की उत्केंद्रता, अतिपरवलय के केंद्र से नाभि और केंद्र से शीर्ष की दूरियों का अनुपात है।

ऐतिहासिक पृष्ठभूमिं

ज्यामिति गणित की सबसे प्राचीन शाखाओं में से एक है। यूनान के ज्यामितिविदों ने अनेक वक्रों के गुणधर्मों का अन्वेषण किया जिनकी सैद्धांतिक और व्यावहारिक महत्ता है। Euclid ने लगभग 300 ई.पू. ज्यामिति पर अपना भाष्य लिखा। वह सर्वप्रथम व्यक्ति थे जिन्होनें भौतिक चिंतन द्वारा सुझाए गए निश्चित अभिग्रहीतियों के आधार पर ज्यामितीय चित्रों को संगठित किया। ज्यामिति, जिसका प्रारंभ भारतियों और यूनानियों ने किया, उसके अध्ययन में उन्होंने बीजगणित की विधियों के अनुप्रयोग को आवश्यक नहीं बताया। ज्यामिति विषय की एकीकरण पहुँच जो Euclid, ने दिया तथा जो सुल्वसूत्रों से प्राप्त थी इत्यादि ने दी, लगभग 1300 वर्षों तक चलती रहीं 200 ई. पू. में Apollonius ने एक पुस्तक, ‘The Conic’ लिखी जो अनेक महत्वपूर्ण अन्वेषणों के साथ शंकु परिच्छेदों के बारे में थी और 18 शताब्दियों तक बेजोड़ रही।

Rene Descartes (1596-1650 A.D.) के नाम पर आधुनिक वेश्लेषिक ज्यामिति को कार्तीय (Cartesian) कहा जाता है जिसकी सार्थकता La Geometry नाम से 1637 ई. में प्रकाशित हुई। परंतु वैश्लेषिक ज्यामिति के मूलभूत सिद्धांत और विधियों को पहले ही Peirre de Farmat (1601-1665 ई.) ने अन्वेषित कर लिया था। दुर्भाग्यवश, Fermates का विषय पर भाष्य, Ad Locus Planos et So LIDOS Isagoge - ‘Introduction to Plane and Solid Loci’ केवल उनकी मृत्यु के बाद 1679 ई. में प्रकाशित हुआ था। इसलिए Descartes की वैश्लेषिक ज्यामिति को अद्वितीय अन्वेषक का श्रेय मिला।

Isaac Barrow ने कार्तीय विधियों के प्रयोग को तिरस्कृत किया। न्यूटन ने वक्रों के समीकरण ज्ञात करने के लिए अज्ञात गुणांको की विधि का प्रयोग किया। उन्होंने अनेक प्रकार के निर्देशांकों, ध्रुवीय (Polar) और द्विध्रुवीय (bipolar) का प्रयोग किया। Leibnitz ने ‘भुज’ (abcissa), ‘कोटि’ (ordinate) और निर्देशांक पदों (Coordinate), का प्रयोग किया। L.Hospital (लगभग 1700 ई.) ने वैश्लेषिक ज्यामिति पर एक महत्वपूर्ण पाठ्य पुस्तक लिखी।

Clairaut (1729 ई.) ने सर्वप्रथम दूरी सूत्र को दिया। यद्यपि यह शुद्ध रूप में था उन्होंने रैखिक समीकरण का अंतःखंड रूप भी दिया। Cramer (1750 ई.) ने औपचारिक रूप से दो निर्देशाक्षों को प्रयोग करके वृत्त का समीकरण

$(y-a)^{2}+(b-x)^{2}=r$ दिया।

उन्होंने उस समय में वैश्लेषिक ज्यामिति का सर्वोत्तम प्रस्तुतीकरण दिया। Monge (1781ई.) ने आधुनिक बिंदु प्रवणता के रूप में रेखा का समीकरण निम्न प्रकार से दिया।

$ y-y^{\prime}=a\left(x-x^{\prime}\right) $

तथा दो रेखाओं के लंबवत होने का प्रतिबंध $a a^{\prime}+1=0$ दिया।

S.F. Lacroix (1765-1843 ई.) प्रसिद्ध पाठ्य पुस्तक लेखक थे, लेकिन उनका वैश्लेषिक ज्यामिति में योगदान कहीं कहीं मिलता है। उन्होंने रेखा के समीकरण का दो बिंदु रूप

$ y-\beta=\frac{\beta^{\prime}-\beta}{\alpha^{\prime}-\alpha}(x-\alpha) $

और $(\alpha, \beta)$ से $y=a x+b$ पर लंब की लंबाई $\frac{(\beta-a \alpha-b)}{\sqrt{1+a^{2}}}$ बताया। उन्होनें दो रेखाओं के मध्यस्थ कोण का सूत्र $\tan \theta=\left(\frac{a^{\prime}-a}{1+a a^{\prime}}\right)$ भी दिया।

यह वास्तव में आश्चर्यजनक है कि वैश्लेषिक ज्यामिति के अन्वेषण के बाद इन मूलभूत आवश्यक सूत्रों को ज्ञात करने के लिए 150 वर्षों से अधिक इंतज़ार करना पड़ा। 1818 ई. में C. Lame, एक सिविल इंजीनियर, ने दो बिंदुपथों $\mathrm{E}=0$ और $\mathrm{E}^{\prime}=0$ के प्रतिच्छेद बिंदु से जाने वाले वक्र $m \mathrm{E}+m^{\prime} \mathrm{E}^{\prime}=0$ को बताया।

विज्ञान एवं गणित दोनों में अनेक महत्वपूर्ण अन्वेषण शंकु परिच्छेदों से संबंधित हैं। यूनानियों विशेषकर Archimedes (287-212 ई.पू.) और Apollonius (200 ई.पू.) ने शंकु परिच्छेदों का अध्ययन किया। आजकल ये वक्र महत्वपूर्ण उपक्रम हैं, जिससे बाह्य अंतरिक्ष और परमाणु कणों के व्यवहार से संबंधित अन्वेषणों के द्वारा अनेक रहस्यों का उद्घाटन हुआ है।