अध्याय 13 सांख्यिकी (Statistics)
सांख्यिकी को औसत और उनके अनुमानों का विज्ञान कहा जा सकता है – ए.एल.बॉली और ए.एल. बोडिंगटन
13.1 भूमिका (Introduction)
हम जानते हैं कि सांख्यिकी का सरोकार किसी विशेष उद्देश्य के लिए एकत्रित आँकड़ों से होता है। हम आँकड़ों का विश्लेषण एवं व्याख्या कर उनके बारे में निर्णय लेते हैं। हमने पिछली कक्षाओं में आँकड़ों को आलेखिक एवं सारणीबद्ध रूप में व्यक्त करने की विधियों का अध्ययन किया है। यह निरूपण आँकड़ों के महत्वपूर्ण गुणों एवं विशेषताओं को दर्शाता है। हमने दिए गए आँकड़ों का एक प्रतिनिधिक मान ज्ञात करने की विधियों के बारे में भी अध्ययन किया है। इस मूल्य को केंद्रीय प्रवृत्ति की माप कहते हैं। स्मरण कीजिए कि माध्य (समांतर माध्य), माध्यिका और बहुलक केंद्रीय प्रवृत्ति की तीन माप हैं। केंद्रीय प्रवृत्ति के माप हमें इस बात का आभास दिलाते

Karl Pearson (1857-1936 A.D.)
हैं कि आँकड़े किस स्थान पर केंद्रित हैं किंतु आँकड़ों के समुचित अर्थ विवेचन के लिए हमें यह भी पता होना चाहिए कि आँकड़ों में कितना बिखराव है या वे केंद्रीय प्रवृत्ति की माप के चारों ओर किस प्रकार एकत्रित हैं।
दो बल्लेबाजों द्वारा पिछले दस मैचों में बनाए गए रनों पर विचार करें:
बल्लेबाज $\mathrm{A}: 30,91,0,64,42,80,30,5,117,71$
बल्लेबाज $\mathrm{B}: 53,46,48,50,53,53,58,60,57,52$
स्पष्टतया आँकड़ों का माध्य व माध्यिका निम्नलिखित हैं:
| बल्लेबाज A | बल्लेबाज B | |
|---|---|---|
| Mean | 53 | 53 |
| Median | 53 | 53 |
स्मरण कीजिए कि हम प्रेक्षणों का माध्य ( $\bar{x}$ द्वारा निरूपित) उनके योग को उनकी संख्या से भाग देकर ज्ञात करते हैं, अर्थात्
$ \bar{x}=\frac{1}{n} \sum\limits_{i=1}^{n} x_i $
माध्यिका की गणना के लिए आँकड़ों को पहले आरोही या अवरोही क्रम में व्यवस्थित किया जाता है और फिर निम्नलिखित नियम लगाया जाता है:
यदि प्रेक्षणों की संख्या विषम है तो माध्यिका $\left(\frac{n+1}{2}\right)$ वाँ प्रेक्षण होती है।
यदि प्रेक्षणों की संख्या सम है तो माध्यिका $\left(\frac{n}{2}\right)$ वें और $\left(\frac{n}{2}+1\right)$ वें प्रेक्षणों का माध्य होती है।
हम पाते हैं कि दोनों बल्लेबाजों $\mathrm{A}$ तथा $\mathrm{B}$ द्वारा बनाए गए रनों का माध्य व माध्यिका बराबर है अर्थात् 53 है। क्या हम कह सकते हैं कि दोनों बल्लेबाजों का प्रदर्शन समान है? स्पष्टता नहीं। क्योंकि $\mathrm{A}$ के रनों में परिवर्तनशीलता 0 (न्यूनतम) से 117 (अधिकतम) तक है। जबकि $\mathrm{B}$ के रनों का विस्तार 46 (न्यूनतम) से 60 (अधिकतम) तक है।
आइए अब उपर्युक्त स्कोरों को एक संख्या रेखा पर अंकित करें। हमें नीचे दर्शाई गई आकृतियाँ प्राप्त होती हैं (आकृति 13.1 और 13.2 )।
बल्लेबाज $A$ के लिए

आकृति 13.1
बल्लेबाज $\mathrm{B}$ के लिए

आकृति 13.2
हम देख सकते हैं कि बल्लेबाज $\mathrm{B}$ के संगत बिंदु एक दूसरे के पास-पास हैं और केंद्रीय प्रवृत्ति की माप (माध्य व माध्यिका) के इर्द गिर्द गुच्छित हैं जबकि बल्लेबाज $\mathrm{A}$ के संगत बिंदुओं में अधिक बिखराव है या वे अधिक फैले हुए हैं।
अतः दिए गए आँकड़ों के बारे में संपूर्ण सूचना देने के लिए केंद्रीय प्रवृत्ति की माप पर्याप्त नहीं हैं। परिवर्तनशीलता एक अन्य घटक है जिसका अध्ययन सांख्यिकी के अंतर्गत किया जाना चाहिए। केंद्रीय प्रवृत्ति की माप की तरह ही हमें परिवर्तनशीलता के वर्णन के लिए एकल संख्या चाहिए। इस संख्या को ‘प्रकीर्णन की माप (Measure of dispersion)’ कहा जाता है। इस अध्याय में हम प्रकीर्णन की माप के महत्व व उनकी वर्गीकृत एवं अवर्गीकृत आँकड़ों के लिए गणना की विधियों के बारे में पढ़ेंगे।
13.2 प्रकीर्णन की माप (Measures of dispersion)
आँकड़ों में प्रकीर्णन या विक्षेपण का माप प्रेक्षणों व वहाँ प्रयुक्त केंद्रीय प्रवृत्ति की माप के आधार पर किया जाता है। प्रकीर्णन के निम्नलिखित माप हैं:
(i) परिसर (Range) (ii) चतुर्थक विचलन (Quartile deviation) (iii) माध्य विचलन (Mean deviation) (iv) मानक विचलन (Standard deviation).
इस अध्याय में हम, चतुर्थक विचलन के अतिरिक्त अन्य सभी मापों का अध्ययन करेंगे।
13.3 परिसर (Range)
स्मरण कीजिए कि दो बल्लेबाजों $\mathrm{A}$ तथा $\mathrm{B}$ द्वारा बनाए गए रनों के उदाहरण में हमने स्कोरों में बिखराव, प्रत्येक श्रृंखला के अधिकतम एवं न्यूनतम रनों के आधार पर विचार किया था। इसमें एकल संख्या ज्ञात करने के लिए हम प्रत्येक शृंखला के अधिकतम व न्यूनतम मूल्यों में अंतर प्राप्त करते हैं। इस अंतर को परिसर कहा जाता है।
बल्लेबाज $\mathrm{A}$ के लिए परिसर $=117-0=117$ और बल्लेबाज $\mathrm{B}$, के लिए परिसर $=60-46=14$ स्पष्टतया परिसर $\mathrm{A}>$ परिसर $\mathrm{B}$, इसलिए $\mathrm{A}$ के स्कोरों में प्रकीर्णन या बिखराव अधिक है जबकि $\mathrm{B}$ के स्कोर एक दूसरे के अधिक पास हैं।
अतः एक शृंखला का परिसर = अधिकतम मान न्यूनतम मान
आँकड़ों का परिसर हमें बिखराव या प्रकीर्णन का मोटा-मोटा (rough) ज्ञान देता है, किंतु केंद्रीय प्रवृत्ति की माप, विचरण के बारे में कुछ नहीं बताता है। इस उद्देश्य के लिए हमें प्रकीर्णन के अन्य माप की आवश्यकता है। स्पष्टतया इस प्रकार की माप प्रेक्षणों की केंद्रीय प्रवृत्ति से अंतर (या विचलन) पर आधारित होनी चाहिए।
केंद्रीय प्रवृत्ति से प्रेक्षणों के अंतर के आधार पर ज्ञात की जाने वाली प्रकीर्णन की महत्वपूर्ण माप माध्य विचलन व मानक विचलन हैं। आइए इन पर विस्तार से चर्चा करें।
13.4 माध्य विचलन (Mean deviation)
याद कीजिए कि प्रेक्षण $x$ का स्थिर मान $a$ से अंतर $(x-a)$ प्रेक्षण $x$ का $a$ से विचलन कहलाता है। प्रेक्षण $x$ का केंद्रीय मूल्य ’ $a$ ’ से प्रकीर्णन ज्ञात करने के लिए हम $a$ से विचलन प्राप्त करते हैं। इन विचलनों का माध्य प्रकीर्णन की निरपेक्ष माप होता है। माध्य ज्ञात करने के लिए हमें विचलनों का योग प्राप्त करना चाहिए, किंतु हम जानते हैं कि केंद्रीय प्रवृत्ति की माप प्रेक्षणों के समुच्चय की अधिकतम तथा न्यूनतम मूल्यों के मध्य स्थित होता है। इसलिए कुछ विचलन ऋणात्मक तथा कुछ धनात्मक होंगे। अतः विचलनों का योग शून्य हो सकता है। इसके अतिरिक्त माध्य $\bar{x}$ से विचलनों का योग शून्य होता है।
साथ ही $\quad \quad \quad $ विचलनों का माध्य $=\frac{\text{ विचलनों का योग }}{\text{ प्रेक्षणों की संख्या }}=\frac{0}{n}=0$
अतः माध्य के सापेक्ष माध्य विचलन ज्ञात करने का कोई औचित्य नहीं है।
स्मरण कीजिए कि प्रकीर्णन की उपर्युक्त माप ज्ञात करने के लिए हमें प्रत्येक मान की केंद्रीय प्रवृत्ति की माप या किसी स्थिर संख्या ’ $a$ ’ से दूरी ज्ञात करनी होती है। याद कीजिए कि किन्हीं दो संख्याओं के अंतर का निरपेक्ष मान उन संख्याओं द्वारा संख्या रेखा पर व्यक्त बिंदुओं के बीच की दूरी को दर्शाता है। अतः स्थिर संख्या ’ $a$ ’ से विचलनों के निरपेक्ष मानों का माध्य ज्ञात करते हैं। इस माध्य को ‘माध्य विचलन’ कहते हैं। अतः केंद्रीय प्रवृत्ति ’ $a$ ’ के सापेक्ष माध्य विचलन प्रेक्षणों का ’ $a$ ’ से विचलनों के निरपेक्ष मानों का माध्य होता है। ’ $a$ ’ के सापेक्ष माध्य विचलन को M.D. (a) द्वारा प्रकट किया जाता है।
$ \text { M.D. }(a)=\frac{{ }^{\prime} a \text { ’ से विचलनों के निरपेक्ष मान का योग }}{\text { प्रेक्षणों की संख्या }} $
टिप्पणी माध्य विचलन केंद्रीय प्रवृत्ति की किसी भी माप से ज्ञात किया जा सकता है। किंतु सांख्यिकीय अध्ययन में सामान्यतः माध्य और माध्यिका के सापेक्ष माध्य विचलन का उपयोग किया जाता है।
13.4.1 अवर्गीकृत आँकडों के लिए माध्य विचलन (Mean deviation for ungrouped
data) मान लीजिए कि $n$ प्रेक्षणों के आँकड़े $x _{1}, x _{2}, x _{3}, \ldots, x _{n}$ दिए गए हैं। माध्य या माध्यिका के सापेक्ष माध्य विचलन की गणना में निम्नलिखित चरण प्रयुक्त होते हैं:
चरण-1 उस केंद्रीय प्रवृत्ति की माप को ज्ञात कीजिए जिससे हमें माध्य विचलन प्राप्त करना है। मान लीजिए यह ’ $a$ ’ है।
चरण-2 प्रत्येक प्रेक्षण $x _{i}$ का $a$ से विचलन अर्थात् $x _{1}-a, x _{2}-a, x _{3}-a, \ldots, x _{n}-a$ ज्ञात करें।
चरण-3 विचलनों का निरपेक्ष मान ज्ञात करें अर्थात् यदि विचलनों में ऋण चिह्न लगा है तो उसे हटा $ \text { दें अर्थात् }\left|x _{1}-a\right|,\left|x _{2}-a\right|,\left|x _{3}-a\right|, \ldots,\left|x _{n}-a\right| \text { ज्ञात करें। } $
चरण-4 विचलनों के निरपेक्ष मानों का माध्य ज्ञात करें। यही माध्य ’ $a$ ’ के सापेक्ष माध्य विचलन है।
$ \text{ M.D. }(a)=\frac{\sum\limits_{i=1}^{n}|x_i-a|}{n} $
अर्थात् $\quad\quad\quad$ M.D. $(\bar{x})=\frac{1}{n} \sum\limits_{i=1}^{n}|x_i-\bar{x}|$,जहाँ $\bar{x}=$ माध्य
तथा $\quad\quad\quad$ $ \text { M.D. }(\mathrm{M})=\frac{1}{n} \sum _{i=1}^{n}\left|x _{i}-\mathrm{M}\right| \text {, जहाँ } \mathrm{M}=\text { माध्यिका } $
टिप्पणी इस अध्याय में माध्यिका को चिह्न $M$ द्वारा निरूपित किया गया है जब तक कि अन्यथा नहीं कहा गया हो। आइए अब उपर्युक्त चरणों को समझने के लिए निम्नलिखित उदाहरण लें:
उदाहरण-1 निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए:
$ 6,7,10,12,13,4,8,12 $
हल हम क्रमबद्ध आगे बढ़ते हुए निम्नलिखित प्राप्त करते हैं:
चरण 1 दिए गए आँकड़ों का माध्य
$ \bar{x}=\frac{6+7+10+12+13+4+8+12}{8}=\frac{72}{8}=9 \text { है। } $
चरण 2 प्रेक्षणों के माध्य $\bar{x}$ से क्रमशः विचलन $x _{\mathrm{i}}-\bar{x}$ अर्थात्
$\quad\quad\quad\quad 6-9,7-9,10-9,12-9,13-9,4-9,8-9,12-9$ हैं।
या $ \quad\quad\quad\quad -3,-2,1,3,4,-5,-1,3 \text { हैं। } $
चरण 3 विचलनों के निरपेक्ष मान $\left|x _{i}-\bar{x}\right|$
$ 3,2,1,3,4,5,1,3 \text { हैं। } $
चरण 4 माध्य के सापेक्ष माध्य विचलन निम्नलिखित है:
$ \begin{aligned} \text { M.D. }(\bar{x}) & =\frac{\sum _{i=1}^{8}\left|x _{i}-\bar{x}\right|}{8} \\ & =\frac{3+2+1+3+4+5+1+3}{8}=\frac{22}{8}=2.75 \end{aligned} $
टिप्पणी प्रत्येक बार चरणों को लिखने के स्थान पर हम, चरणों का वर्णन किए बिना ही क्रमानुसार परिकलन कर सकते हैं।
उदाहरण 2 निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए:
$ 12,3,18,17,4,9,17,19,20,15,8,17,2,3,16,11,3,1,0,5 $
हल हमें दिए गए आँकड़ों का माध्य $(\bar{x})$ ज्ञात करना होगा।
$ \bar{x}=\frac{1}{20} \sum _{i=1}^{20} x _{i}=\frac{200}{20}=10 $
माध्य से विचलनों के निरपेक्ष मान अर्थात् $\left|x _{i}-\bar{x}\right|$ इस प्रकार हैं:
$ 2,7,8,7,6,1,7,9,10,5,2,7,8,7,6,1,7,9,10,5 $
इसलिए $\quad \sum _{i=1}^{20}\left|x _{i}-\bar{x}\right|=124$
और $ \quad\quad\quad\quad\text { M.D. }(\bar{x})=\frac{124}{20}=6.2 $
उदाहरण 3 निम्नलिखित आँकड़ों से माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए:
$ 3,9,5,3,12,10,18,4,7,19,21 $
हल यहाँ प्रक्षेणों की संख्या 11 है जो विषम है। आँकड़ों को आरोही क्रम में लिखने पर हमें $3,3,4$, $5,7,9,10,12,18,19,21$ प्राप्त होता है।
अब
माध्यिका $=\left(\frac{11+1}{2}\right)$ वाँ या 6 वाँ प्रेक्षण $=9$ है।
विचलनों का क्रमशः निरपेक्ष मान $\left|x _{i}-\mathrm{M}\right|$ इस प्रकार से है। $ 6,6,5,4,2,0,1,3,9,10,12 $
इसलिए $\quad\quad\quad\quad\quad \sum _{i=1}^{11}\left|x _{i}-\mathrm{M}\right|=58$
तथा $ \quad\quad\quad\quad\text { M.D. }(\mathrm{M})=\frac{1}{11} \sum _{i=1}^{11}\left|x _{i}-\mathrm{M}\right|=\frac{1}{11} \times 58=5.27 $
13.4.2 वर्गीकृत आँकड़ों के लिए माध्य विचलन (Mean deviation for grouped data)
हम जानते हैं कि आँकड़ों को दो प्रकार से वर्गीकृत किया जाता है।
(a) असतत बारंबारता बंटन (Discrete frequency distribution)
(b) सतत बारंबारता बंटन (Continuous frequency distribution)
आइए इन दोनों प्रकार के आँकड़ों के लिए माध्य विचलन ज्ञात करने की विधियों पर चर्चा करें।
(a) असतत बारंबारता बंटन मान लीजिए कि दिए गए आँकड़ों में $n$ भिन्न प्रेक्षण $x _{1}, x _{2}, \ldots, x _{n}$ हैं जिनकी बारंबारताएँ क्रमशः $f _{1}, f _{2}, \ldots, f _{n}$ हैं। इन आँकड़ों को सारणीबद्ध रूप में निम्नलिखित प्रकार से व्यक्त किया जा सकता है जिसे असतत बारंबारता बंटन कहते हैं:
$ \begin{matrix} x: x_1 & x_2 & x_3 \ldots x_n \\ f: f_1 & f_2 & f_3 \ldots f_n \end{matrix} $
(i) माध्य के सापेक्ष माध्य विचलन
सर्वप्रथम हम दिए गए आँकड़ों का निम्नलिखित सूत्र द्वारा माध्य $\bar{x}$ ज्ञात करते हैं:
$ \bar{x}=\frac{\sum _{i=1}^{n} x _{i} f _{i}}{\sum _{i=1}^{n} f _{i}}=\frac{1}{\mathrm{~N}} \sum _{i=1}^{n} x _{i} f _{i} $
जहाँ $\sum _{i=1}^{n} x _{i} f _{i}$ प्रेक्षणों $x _{i}$ का उनकी क्रमशः बारंबारता $f _{i}$ से गुणनफलों का योग प्रकट करता है। तथा $\mathrm{N}=\sum _{i=1}^{n} f _{i}$ बारंबारताओं का योग है।
तब हम प्रेक्षणों $x _{i}$ का माध्य $\bar{x}$ से विचलन ज्ञात करते हैं और उनका निरपेक्ष मान लेते हैं अर्थात सभी $i=1,2, \ldots, n$ के लिए $\left|x _{i}-\bar{x}\right|$ ज्ञात करते हैं।
इसके पश्चात् विचलनों के निरपेक्ष मान का माध्य ज्ञात करते हैं, जोकि माध्य के सापेक्ष वांछित माध्य विचलन है। अत:
$\quad$ M.D. $(\bar{x})=\frac{\sum _{i=1}^{n} f _{i}\left|x _{i}-\bar{x}\right|}{\sum f _{i}}=\frac{1}{\mathrm{~N}} \sum _{i=1}^{n} f _{i}\left|x _{i}-\bar{x}\right|$
(ii) माध्यिका के सापेक्ष माध्य विचलन माध्यिका के सापेक्ष माध्य विचलन ज्ञात करने के लिए हम दिए गए असतत बारंबारता बंटन की माध्यिका ज्ञात करते हैं। इसके लिए प्रेक्षणों को आरोही क्रम में व्यवस्थित करते हैं। इसके पश्चात् संचयी बांरबारताएँ ज्ञात की जाती हैं। तब उस प्रेक्षण का निर्धारण करते हैं जिसकी संचयी बांरबारता $\frac{\mathrm{N}}{2}$, के समान या इससे थोड़ी अधिक है। यहाँ बारंबारताओं का योग $\mathrm{N}$ से दर्शाया गया है। प्रेक्षणों का यह मान आँकड़ों के मध्य स्थित होता है इसलिए यह अपेक्षित माध्यिका है। माध्यिका ज्ञात करने के बाद हम माध्यिका से विचलनों के निरपेक्ष मानों का माध्य ज्ञात करते हैं। इस प्रकार
$ \text { M.D.(M) }=\frac{1}{\mathrm{~N}} \sum _{i=1}^{n} f _{i}\left|x _{i}-\mathrm{M}\right| $
उदाहरण 4 निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए:
| $x _{i}$ | 2 | 5 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| $f _{i}$ | 2 | 8 | 10 | 7 | 8 | 5 |
हल आइए दिए गए आँकड़ों की सारणी 13.1 बनाकर अन्य स्तंभ परिकलन के बाद लगाएँ
सारणी 13.1
| $x _{i}$ | $f _{i}$ | $f _{i} x _{i}$ | $\left|x _{i}-\bar{x}\right|$ | $f _{\mathrm{i}}\left|x _{i}-\bar{x}\right|$ |
|---|---|---|---|---|
| 2 | 2 | 4 | 5.5 | 11 |
| 5 | 8 | 40 | 2.5 | 20 |
| 6 | 10 | 60 | 1.5 | 15 |
| 8 | 7 | 56 | 0.5 | 3.5 |
| 10 | 8 | 80 | 2.5 | 20 |
| 12 | 5 | 60 | 4.5 | 22.5 |
| 40 | 300 | 92 |
$ N=\sum\limits_{i=1}^{6} f_i=40, \quad \sum\limits_{i=1}^{6} f_i x_i=300, \quad \sum\limits_{i=1}^{6} f_i|x_i-\bar{x}|=92 $
इसलिए $ \quad \quad \quad\bar{x}=\frac{1}{\mathrm{~N}} \sum _{i=1}^{6} f _{i} x _{i}=\frac{1}{40} \times 300=7.5 $
और $ \quad \quad \quad\text { M.D. }(\bar{x})=\frac{1}{\mathrm{~N}} \sum _{i=1}^{6} f _{i}\left|x _{i}-\bar{x}\right|=\frac{1}{40} \times 92=2.3 $
उदाहरण 5 निम्नलिखित आँकड़ों के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए:
| $x _{i}$ | 3 | 6 | 9 | 12 | 13 | 15 | 21 | 22 |
|---|---|---|---|---|---|---|---|---|
| $f _{i}$ | 3 | 4 | 5 | 2 | 4 | 5 | 4 | 3 |
हल दिए गए आँकड़े पहले ही आरोही क्रम में हैं। इन आँकड़ों में संगत संचयी बारंबारता की एक कतार और लगाते हैं (सारणी 13.2)।
सारणी 13.2
| $x _{i}$ | 3 | 6 | 9 | 12 | 13 | 15 | 21 | 22 |
|---|---|---|---|---|---|---|---|---|
| $f _{i}$ | 3 | 4 | 5 | 2 | 4 | 5 | 4 | 3 |
| c.f. | 3 | 7 | 12 | 14 | 18 | 23 | 27 | 30 |
अब, $\mathrm{N}=30$ है जो सम संख्या है,
इसलिए माध्यिका 15 वीं व 16 वीं प्रेक्षणों का माध्य है। यह दोनों प्रेक्षण संचयी बारंबारता 18 में स्थित हैं जिसका संगत प्रेक्षण 13 है।
इसलिए माध्यिका $\mathrm{M}=\frac{15 \text { वाँ प्रेक्षण }+16 \text { वाँ प्रेक्षण }}{2}=\frac{13+13}{2}=13$
अब माध्यिका से विचलनों का निरपेक्ष मान अर्थात् $\left|x _{i}-\mathrm{M}\right|$ निम्नलिखित सारणी 13.3 में दर्शाए गए हैं।
सारणी 13.3
| $\left|x _{i}-\mathrm{M}\right|$ | 10 | 7 | 4 | 1 | 0 | 2 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| $f _{\mathrm{i}}$ | 3 | 4 | 5 | 2 | 4 | 5 | 4 | 3 |
| $f _{\mathrm{i}}\left|x _{i}-\mathrm{M}\right|$ | 30 | 28 | 20 | 2 | 0 | 10 | 32 | 27 |
$ \quad \quad \quad \sum\limits_{i=1}^{8} f_i=30 \text{ and } \sum\limits_{i=1}^{8} f_i|x_i-M|=149 $
इसलिए
$ \begin{aligned} \text{ M. D. }(M) & =\frac{1}{N} \sum\limits_{i=1}^{8} f_i|x_i-M| \\ & =\frac{1}{30} \times 149=4.97 \end{aligned} $
(b) सतत बारंबारता बंटन एक सतत बांरबारता बंटन वह भृंखला होती है जिसमें आँकड़ों को विभिन्न बिना अंतर वाले वर्गों में वर्गीकृत किया जाता है और उनकी क्रमशः बारंबारता लिखी जाती है।
उदाहरण के लिए 100 छात्रों द्वारा प्राप्ताकों को सतत बांरबारता बंटन में निम्नलिखित प्रकार से व्यक्त किया गया है:
| प्राप्त अंक | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
|---|---|---|---|---|---|---|
| छात्रों की संख्या | 12 | 18 | 27 | 20 | 17 | 6 |
(i) माध्य के सापेक्ष माध्य विचलन एक सतत बांरबारता बंटन के माध्य की गणना के समय हमने यह माना था कि प्रत्येक वर्ग (Class ) की बारंबारता उसके मध्य-बिंदु पर केंद्रित होती है। यहाँ भी हम प्रत्येक वर्ग का मध्य-बिंदु लिखते हैं और असतत बारंबारता बंटन की तरह माध्य विचलन ज्ञात करते हैं।
आइए निम्नलिखित उदाहरण देखें
उदाहरण 6 निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए:
| प्राप्तांक | $10-20$ | $20-30$ | $30-40$ | $40-50$ | $50-60$ | $60-70$ | $70-80$ |
|---|---|---|---|---|---|---|---|
| छात्रों की संख्या | 2 | 3 | 8 | 14 | 8 | 3 | 2 |
हल दिए गए आँकड़ों से निम्न सारणी 13.4 बनाते हैं।
सारणी 13.4
| प्राप्तांक | छात्रों की संख्या |
मध्य-बिंदु | $f _{i} x _{i}$ | $\left|x _{i}-\bar{x}\right|$ | $f _{\mathrm{i}}\left|x _{i}-\bar{x}\right|$ |
|---|---|---|---|---|---|
| $10-20$ | 2 | 15 | 30 | 30 | 60 |
| $20-30$ | 3 | 25 | 75 | 20 | 60 |
| $30-40$ | 8 | 35 | 280 | 10 | 80 |
| $40-50$ | 14 | 45 | 630 | 0 | 0 |
| $50-60$ | 8 | 55 | 440 | 10 | 80 |
| $60-70$ | 3 | 65 | 195 | 20 | 60 |
| $70-80$ | 2 | 75 | 150 | 30 | 60 |
| 40 | 1800 | 400 |
यहाँ $ \quad \quad \quad N=\sum\limits_{i=1}^{7} f_i=40, \sum\limits_{i=1}^{7} f_i x_i=1800, \sum\limits_{i=1}^{7} f_i|x_i-\bar{x}|=400 $
इसलिए $\quad \quad \quad\bar{x}=\frac{1}{N} \sum\limits_{i=1}^{7} f_i x_i=\frac{1800}{40}=45$
और $ \quad \quad \quad\text{ M.D. }(\bar{x})=\frac{1}{N} \sum\limits_{i=1}^{7} f_i|x_i-\bar{x}|=\frac{1}{40} \times 400=10 $
माध्य के सापेक्ष माध्य विचलन ज्ञात करने की लघु विधि हम पद विचलन विधि
(Stepdeviation method) का प्रयोग करके $\bar{x}$ के कठिन परिकलन से बच सकते हैं। स्मरण कीजिए कि इस विधि में हम आँकड़ों के मध्य या उसके बिल्कुल पास किसी प्रेक्षण को कल्पित माध्य लेते हैं। तब प्रेक्षणों (या विभिन्न वर्गों के मध्य-बिंदुओं) का इस कल्पित माध्य से विचलन ज्ञात करते हैं। यह विचलन संख्या रेखा पर मूल बिंदु (origin) को शून्य से प्रतिस्थापित कर कल्पित माध्य पर ले जाना ही होता है, जैसा कि आकृति 13.3 में दशार्या गया है।
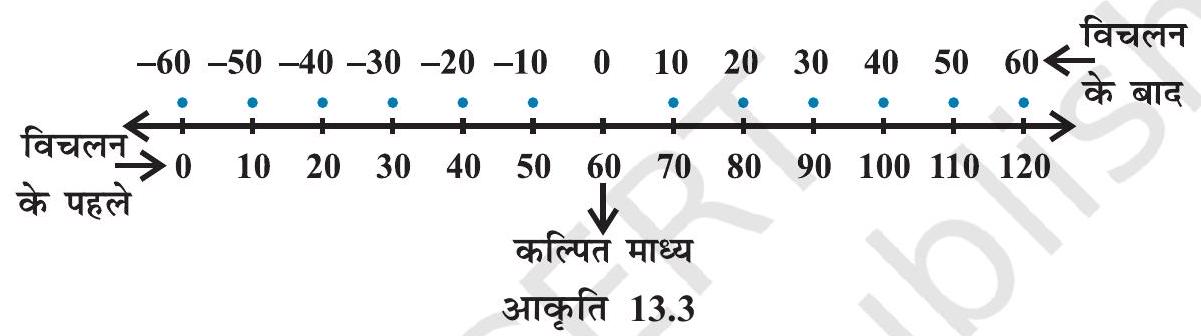
आकृति 13.3
यदि सभी विचलनों में कोई सार्व गुणनखंड (common factor) है तो विचलनों को सरल करने के लिए इन्हें इस सार्व गुणनखंड से भाग देते हैं। इन नए विचलनों को पद विचलन कहते हैं। पद विचलन लेने की प्रक्रिया संख्या रेखा पर पैमाने का परिवर्तन होता है, जैसा कि आकृति 13.4 में दर्शाया गया है।
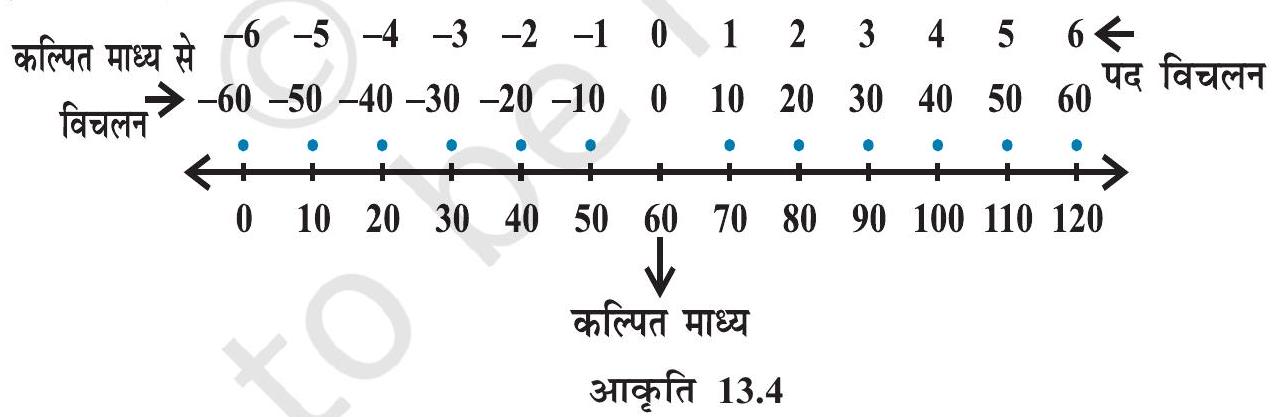
विचलन और पद विचलन प्रेक्षणों के आकार को छोटा कर देते हैं, जिससे गुणन जैसी गणनाएँ सरल हो जाती हैं। मान लीजिए नया चर $d _{i}=\frac{x _{i}-a}{h}$ हो जाता है, जहाँ ’ $a$ ’ कल्पित माध्य है व $h$ सार्व गुणनखंड है। तब पद विचलन विधि द्वारा $\bar{x}$ निम्नलिखित सूत्र से ज्ञात किया जाता है:
$ \bar{x}=a+\frac{\sum _{i=1}^{n} f _{i} d _{i}}{\mathrm{~N}} \times h $
आइए उदाहरण 6 के आँकड़ों के लिए पद विचलन विधि लगाएँ।
हम कल्पित माध्य $a=45$ और $h=10$, लेते हैं और निम्नलिखित सारणी 13.5 बनाते हैं।
सारणी 13.5
| प्राप्तांक | छात्रों की संख्या |
मध्य-बिंदु | $d _{i}=\frac{x _{i}-45}{10}$ | $f _{i} d _{i}$ | $\left|x _{i}-\bar{x}\right|$ | $f _{\mathrm{i}}\left|x _{i}-\bar{x}\right|$ |
|---|---|---|---|---|---|---|
| $f _{i}$ | $x _{i}$ | |||||
| $10-20$ | 2 | 15 | -3 | -6 | 30 | 60 |
| $20-30$ | 3 | 25 | -2 | -6 | 20 | 60 |
| $30-40$ | 8 | 35 | -1 | -8 | 10 | 80 |
| $40-50$ | 14 | 45 | 0 | 0 | 0 | 0 |
| $50-60$ | 8 | 55 | 1 | 8 | 10 | 80 |
| $60-70$ | 3 | 65 | 2 | 6 | 20 | 60 |
| $70-80$ | 2 | 75 | 3 | 6 | 30 | 60 |
| 40 | 0 | 400 |
इसलिए
$ \begin{aligned} & \bar{x}=a+\frac{\sum\limits_{i=1}^{7} f_i d_i}{N} \times h \\ & =45+\frac{0}{40} \times 10=45 \end{aligned} $
and $ \quad \quad \quad \text{ M.D. }(\bar{x})=\frac{1}{N} \sum\limits_{i=1}^{7} f_i|x_i-\bar{x}|=\frac{400}{40}=10 $
टिप्पणी पद विचलन विधि का उपयोग $\bar{x}$ ज्ञात करने के लिए किया जाता है। शेष प्रक्रिया वैसी ही है।
(ii) माध्यिका के सापेक्ष माध्य विचलन दिए गए आँकड़ों के लिए माध्यिका से माध्य विचलन ज्ञात करने की प्रक्रिया वैसी ही है जैसी कि हमने माध्य के सापेक्ष माध्य विचलन ज्ञात करने के लिए की थी। इसमें विशेष अंतर केवल विचलन लेने के समय माध्य के स्थान पर माध्यिका लेने में होता है।
आइए सतत बारंबारता बटंन के लिए माध्यिका ज्ञात करने की प्रक्रिया का स्मरण करें।
आँकडों को पहले आरोही क्रम में व्यवस्थित करते हैं। तब सतत बारंबारता बंटन की माध्यिका ज्ञात करने के लिए पहले उस वर्ग को निर्धारित करते हैं जिसमें माध्यिका स्थित होती है (इस वर्ग को माध्यिका वर्ग कहते हैं) और तब निम्नलिखित सूत्र लगाते हैं:
$ \text{ माध्यिका }=l+\frac{\frac{N}{2}-C}{f} \times h $
जहाँ माध्यिका वर्ग वह वर्ग है जिसकी संचयी बारंबारता $\frac{\mathrm{N}}{2}$ के बराबर या उससे थोड़ी अधिक हो, बांरबारताओं का योग $\mathrm{N}$, माध्यिका वर्ग की निम्न सीमा $l$, माध्यिका वर्ग की बांरबारता $f$, माध्यिका वर्ग से सटीक पहले वाले वर्ग की संचयी बारंबारता $\mathrm{C}$ और माध्यिका वर्ग का विस्तार $h$ है। माध्यिका ज्ञात करने के पश्चात् प्रत्येक वर्ग के मध्य-बिंदुओं $x _{i}$ का माध्यिका से विचलनों का निरपेक्ष मान अर्थात् $\left|x _{i}-\mathrm{M}\right|$ प्राप्त करते हैं।
तब $ \quad \quad \quad \text{ M.D. }(M)=\frac{1}{N} \sum\limits_{i=1}^{n} f_i|x_i-M| $
इस प्रक्रिया को निम्नलिखित उदाहरण से स्पष्ट किया गया है:
उदाहरण 7 निम्नलिखित आँकड़ों के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए।
| वर्ग | $0-10$ | $10-20$ | $20-30$ | $30-40$ | $40-50$ | $50-60$ |
|---|---|---|---|---|---|---|
| बारंबारता | 6 | 7 | 15 | 16 | 4 | 2 |
हल दिए गए आँकड़ों से निम्न सारणी 13.6 बनाते हैं:
सारणी 13.6
| वर्ग | बारंबारता | संचयी बारंबारता | मध्य-बिंदु | $\mid x _{i}$-Med. $\mid$ | $f _{i} \mid x _{i}$-Med. $\mid$ |
|---|---|---|---|---|---|
| $f _{i}$ | $(c . f)$. | $x _{i}$ | |||
| $0-10$ | 6 | 6 | 5 | 23 | 138 |
| $10-20$ | 7 | 13 | 15 | 13 | 91 |
| $20-30$ | 15 | 28 | 25 | 3 | 45 |
| $30-40$ | 16 | 44 | 35 | 7 | 112 |
| $40-50$ | 4 | 48 | 45 | 17 | 68 |
| $50-60$ | 2 | 50 | 55 | 27 | 54 |
| 50 | 508 |
यहाँ $\mathrm{N}=50$, इसलिए $\frac{\mathrm{N}}{2}$ वीं या 25 वीं मद 20-30 वर्ग में हैं। इसलिए 20-30 माध्यिका वर्ग है। हम जानते हैं कि
$ \text { माध्यिका }=l+\frac{\frac{\mathrm{N}}{2}-C}{f} \times h $
यहाँ $l=20, \mathrm{C}=13, f=15, h=10$ और $\mathrm{N}=50$
इसलिए, $\quad$ माध्यिका $=20+\frac{25-13}{15} \times 10=20+8=28$
अतः, माध्यिका के सापेक्ष माध्य विचलन
$ \text{ M.D. }(M)=\frac{1}{N} \sum\limits_{i=1}^{6} f_i|x_i-M|=\frac{1}{50} \times 508=10.16 $
प्रश्नावली 13.1
प्रश्न 1 व 2 में दिए गए आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए।
1. $4,7,8,9,10,12,13,17$
Show Answer
\missing2. $38,70,48,40,42,55,63,46,54,44$
Show Answer
\missingप्रश्न 3 व 4 के आँकड़ों के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए।
3. $13,17,16,14,11,13,10,16,11,18,12,17$
Show Answer
\missing4. $36,72,46,42,60,45,53,46,51,49$
Show Answer
\missingप्रश्न 5 व 6 के आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए।
5. $\begin{array}{llllll} x_i & 5 & 10 & 15 & 20 & 25 \\ f_i & 7 & 4 & 6 & 3 & 5 \\ \end{array}$
Show Answer
\missing6. $\begin{array}{llllll} x_i & 10 & 30 & 50 & 70 & 90 \\ f_i & 4 & 24 & 28 & 16 & 8 \end{array}$
Show Answer
\missingप्रश्न 7 व 8 के आँकड़ों के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए।
7. $\begin{array}{llllll} x_i 5 & 7 & 9 & 10 & 12 & 15 \\ f_i 8 & 6 & 2 & 2 & 2 & 6 \end{array}$
Show Answer
\missing8. $\begin{array}{llllll} x_i 5 & 7 & 9 & 10 & 12 & 15 \\ f_i 8 & 6 & 2 & 2 & 2 & 6 \end{array}$
Show Answer
\missingप्रश्न 9 व 10 के आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिए।
9.
| आय प्रतिदिन (₹ में) |
$0-100$ | $100-200$ | $200-300$ | $300-400$ | $400-500$ | $500-600$ | $600-700$ | $700-800$ |
|---|---|---|---|---|---|---|---|---|
| व्यक्तियों की संख्या |
4 | 8 | 9 | 10 | 7 | 5 | 4 | 3 |
| ऊँचाई (cm में) |
$95-105$ | $105-115$ | $115-125$ | $125-135$ | $135-145$ | $145-155$ | ||
| लड़कों की संख्या |
9 | 13 | 26 | 30 | 12 | 10 |
Show Answer
\missing10.
| सेमी में ऊंचाई | 95-105 | 105-115 | 115-12 | 125 -135 | 135-145 | 145-155 | ||
|---|---|---|---|---|---|---|---|---|
| लड़कों की संख्या | 9 | 13 | 26 | 30 | 12 | 10 |
Show Answer
\missing11. निम्नलिखित आँकड़ों के लिए माध्यिका के सापेक्ष माध्य विचलन ज्ञात कीजिए:
| अंक | $0-10$ | $10-20$ | $20-30$ | $30-40$ | $40-50$ | $50-60$ |
|---|---|---|---|---|---|---|
| लड़कियों की संख्या |
6 | 8 | 14 | 16 | 4 | 2 |
Show Answer
\missing12. नीचे दिए गए 100 व्यक्तियों की आयु के बंटन की माध्यिका आयु के सापेक्ष माध्य विचलन की गणना कीजिए:
| आयु (वर्ष में) | $16-20$ | $21-25$ | $26-30$ | $31-35$ | $36-40$ | $41-45$ | $46-50$ | $51-55$ |
|---|---|---|---|---|---|---|---|---|
| संख्या | 5 | 6 | 12 | 14 | 26 | 12 | 16 | 9 |
[संकेत प्रत्येक वर्ग की निम्न सीमा में से 0.5 घटा कर व उसकी उच्च सीमा में 0.5 जोड़ कर दिए गए आँकड़ों को सतत बारंबारता बंटन में बदलिए]
Show Answer
\missing13.4.3 माध्य विचलन की परिसीमाएँ (Limitations of mean deviation)
बहुत अधिक विचरण या बिखराव वाली शृंखलाओं में माध्यिका केंद्रीय प्रवृत्ति की उपयुक्त माप नहीं होती है। अतः इस दशा में माध्यिका के सापेक्ष माध्य विचलन पर पूरी तरह विश्वास नहीं किया जा सकता है। माध्य से विचलनों का योग (ऋण चिह्न को छोड़कर) माध्यिका से विचलनों के योग से अधिक होता है। इसलिए माध्य के सापेक्ष माध्य विचलन अधिक वैज्ञानिक नहीं है। अतः कई दशाओं में माध्य विचलन असंतोषजनक परिणाम दे सकता है। साथ ही माध्य विचलन को विचलनों के निरपेक्ष मान पर ज्ञात किया जाता है। इसलिए यह और बीजगणितीय गणनाओं के योग्य नहीं होता है। इसका अभिप्राय है कि हमें प्रकीर्णन की अन्य माप की आवश्यकता है। मानक विचलन प्रकीर्णन की ऐसी ही एक माप है।
13.5 प्रसरण और मानक विचलन (Variance and Standard Deviation)
याद कीजिए कि केंद्रीय प्रवृत्ति की माप के सापेक्ष माध्य विचलन ज्ञात करने के लिए हमने विचलनों के निरपेक्ष मानों का योग किया था। ऐसा माध्य विचलन को सार्थक बनाने के लिए किया था, अन्यथा विचलनों का योग शून्य हो जाता है।
विचलनों के चिह्नों के कारण उत्पन्न इस समस्या को विचलनों के वर्ग लेकर भी दूर किया जा सकता है। निसंदेह यह स्पष्ट है कि विचलनों के यह वर्ग ऋणेतर होते हैं।
माना $x _{1}, x _{2}, x _{3}, \ldots, x _{n}, n$ प्रेक्षण हैं तथा $\bar{x}$ उनका माध्य है। तब $ (x _ 1 - \bar {x}) ^ {2} + (x _ 2 - \bar {x} ) ^ {2} + \ldots \ldots . + (x _ {n} - \bar {x} ) ^ {2} = _ {i \neq 1} ^ {n}(x _ {i} - \bar{x})^{2} $
यदि यह योग शून्य हो तो प्रत्येक $\left(x _{i}-\bar{x}\right)$ शून्य हो जाएगा। इसका अर्थ है कि किसी प्रकार का विचरण नहीं है क्योंकि तब सभी प्रेक्षण $\bar{x}$ के बराबर हो जाते हैं।
यदि $\sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2}$ छोटा है तो यह इंगित करता है कि प्रेक्षण $x _{1}, x _{2}, x _{3}, \ldots, x _{n}$, माध्य $\bar{x}$ के निकट हैं तथा प्रेक्षणों का माध्य $\bar{x}$ के सापेक्ष विचरण कम है । इसके विपरीत यदि यह योग बड़ा है तो प्रेक्षणों का माध्य $\bar{x}$ के सापेक्ष विचरण अधिक है। क्या हम कह सकते हैं कि योग $\sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2}$ सभी प्रेक्षणों का माध्य $\bar{x}$ के सापेक्ष प्रकीर्णन या विचरण की माप का एक संतोषजनक प्रतीक है?
आइए इसके लिए छ: प्रेक्षणों $5,15,25,35,45,55$ का एक समुच्चय $\mathrm{A}$ लेते हैं। इन प्रेक्षणों का माध्य 30 है। इस समुच्चय में $\bar{x}$ से विचलनों के वर्ग का योग निम्नलिखित है:
$ \begin{aligned} \sum _{i=1}^{6}\left(x _{i}-\bar{x}\right)^{2} & =(5-30)^{2}+(15-30)^{2}+(25-30)^{2}+(35-30)^{2}+(45-30)^{2}+(55-30)^{2} \\ & =625+225+25+25+225+625=1750 \end{aligned} $
एक अन्य समुच्चय $\mathrm{B}$ लेते हैं जिसके 31 प्रेक्षण निम्नलिखित हैं: $15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37$, $38,39,40,41,42,43,44,45$. इन प्रेक्षणों का माध्य $\bar{y}=30$ है।
दोनों समुच्चयों $\mathrm{A}$ तथा $\mathrm{B}$ के माध्य 30 है।
समुच्चय $\mathrm{B}$ के प्रेक्षणों के विचलनों के वर्गों का योग निम्नलिखित है।
$ \begin{aligned} \sum\limits_{i=1}^{31}(y_i-\bar{y})^{2} & =(15-30)^{2}+(16-30)^{2}+(17-30)^{2}+\ldots+(44-30)^{2}+(45-30)^{2} \\ & =(-15)^{2}+(-14)^{2}+\ldots+(-1)^{2}+0^{2}+1^{2}+2^{2}+3^{2}+\ldots+14^{2}+15^{2} \\ & =2[15^{2}+14^{2}+\ldots+1^{2}] \\ & =2 \times \frac{15 \times(15+1)(30+1)}{6}=5 \times 16 \times 31=2480 \end{aligned} $
(क्योंकि प्रथम $n$ प्राकृत संख्याओं के वर्गों का योग $=\frac{n(n-1)(2 n-1)}{6}$ होता है, यहाँ $n=15$ है)
$ \text { यदि } \sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2} \text { ही माध्य के सापेक्ष प्रकीर्णन की माप हो तो हम कहने के लिए प्रेरित होंगे } $ कि 31 प्रेक्षणों के समुच्चय $\mathrm{B}$ का, 6 प्रेक्षणों वाले समुच्चय $\mathrm{A}$ की अपेक्षा माध्य के सापेक्ष अधिक प्रकीर्णन है यद्यपि समुच्चय $\mathrm{A}$ में 6 प्रेक्षणों का माध्य $\bar{x}$ के सापेक्ष बिखराव (विचलनों का परिसर -25 से 25 है) समुच्चय $\mathrm{B}$ की अपेक्षा (विचलनों का परिसर -15 से 15 है) अधिक है।
यह नीचे दिए गए चित्रों से भी स्पष्ट है:
समुच्चय $\mathrm{A}$, के लिए हम आकृति 13.5 पाते हैं।

आकृति 13.5
समुच्चय $\mathrm{B}$, के लिए आकृति 13.6 हम पाते हैं

आकृति 13.6
अतः हम कह सकते हैं कि माध्य से विचलनों के वर्गों का योग प्रकीर्णन की उपयुक्त माप नहीं है। इस कठिनाई को दूर करने के लिए हम विचलनों के वर्गों का माध्य लें अर्थात् हम $\frac{1}{n} \sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2}$. लें। समुच्चय $\mathrm{A}$, के लिए हम पाते हैं, माध्य $=\frac{1}{6} \times 1750=291.6$ है और समुच्चय $\mathrm{B}$, के लिए यह $\frac{1}{31} \times 2480=80$ है।
यह इंगित करता है कि समुच्चय $\mathrm{A}$ में बिखराव या विचरण समुच्चय $\mathrm{B}$ की अपेक्षा अधिक है जो दोनों समुच्चयों के अपेक्षित परिणाम व ज्यामितिय निरूपण से मेल खाता है।
अतः हम $\frac{1}{n} \sum\left(x _{i}-\bar{x}\right)^{2}$ को प्रकीर्णन की उपयुक्त माप के रूप में ले सकते हैं। यह संख्या अर्थात् माध्य से विचलनों के वर्गों का माध्य प्रसरण (variance) कहलाता है और $\sigma^{2}$ (सिगमा का वर्ग पढ़ा जाता है) से दर्शाते हैं। अतः $n$ प्रेक्षणों $x _{1}, x _{2}, \ldots, x _{n}$ का प्रसरण
$ \sigma^{2}=\frac{1}{n} \sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2} \text { है। } $
13.5.1 मानक विचलन (Standard Deviation)
प्रसरण की गणना में हम पाते हैं कि व्यक्तिगत प्रेक्षणों $x _{i}$ तथा $\bar{x}$ की इकाई प्रसरण की इकाई से भिन्न है, क्योंकि प्रसरण में $\left(x _{i}-\bar{x}\right)$ के वर्गों का समावेश है, इसी कारण प्रसरण के धनात्मक वर्गमूल को प्रेक्षणों का माध्य के सापेक्ष प्रकीर्णन की यथोचित माप के रूप में व्यक्त किया जाता है और उसे मानक विचलन कहते हैं। मानक विचलन को सामान्यतः $\sigma$, द्वारा प्रदर्शित किया जाता है तथा निम्नलिखित प्रकार से दिया जाता है:
$$ \sigma=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}(x_i-\bar{x})^{2}} \quad \quad \quad \quad \quad \ldots(1) $$
आइए अवर्गीकृत आँकड़ों का प्रसरण व मानक विचलन ज्ञात करने के लिए कुछ उदाहरण लेते हैं।
उदाहरण 8 निम्नलिखित आँकड़ों के लिए प्रसरण तथा मानक विचलन ज्ञात कीजिए:
$$ 6,8,10,12,14,16,18,20,22,24 $$
हल दिए गए आँकड़ों को निम्नलिखित प्रकार से सारणी 13.7 में लिख सकते हैं। माध्य को पद विचलन विधि द्वारा 14 को कल्पित माध्य लेकर ज्ञात किया गया है। प्रेक्षणों की संख्या $n=10$ है।
सारणी 13.7
| $x _{i}$ | $d _{i}=\frac{x _{i}-14}{2}$ | माध्य से विचलन $\left(x _{i}-\bar{x}\right)$ |
$\left(x _{i}-\bar{x}\right)$ |
|---|---|---|---|
| 6 | -4 | -9 | 81 |
| 8 | -3 | -7 | 49 |
| 10 | -2 | -5 | 25 |
| 12 | -1 | -3 | 9 |
| 14 | 0 | -1 | 1 |
| 16 | 1 | 1 | 1 |
| 18 | 2 | 3 | 9 |
| 20 | 3 | 5 | 25 |
| 22 | 4 | 7 | 49 |
| 24 | 5 | 9 | 81 |
| 5 | 330 |
इसलिए,
माध्य $\bar{x}=$ कल्पित माध्य $+\frac{\sum _{i=1}^{n} d _{i}}{n} \times h$ $ =14+\frac{5}{10} \times 2=15 $
और
प्रसरण $\sigma^{2}=\frac{1}{n} \sum _{i=1}^{10}\left(x _{i}-\bar{x}\right)^{2}=\frac{1}{10} \times 330=33$
अतः मानक विचलन $\sigma=\sqrt{33}=5.74$
13.5.2 एक असतत बारंबारता बंटन का मानक विचलन (Standard deviation of $a$ discrete frequency distribution)
मान लें दिया गया असतत बंटन निम्नलिखित है:
$ \begin{matrix} x: & x_1, & x_2, \quad x_3, \ldots, x_n \\ \\ & f: & f_1, \quad f_2, \quad f_3, \ldots, f_n \end{matrix} $
इस बंटन के लिए मानक विचलन $(\sigma)=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{n} f_i(x_i-\bar{x})^{2}} \quad \quad \quad \quad \ldots(2)$
जहाँ $N=\sum\limits_{i=1}^{n} f_i$.
आइए निम्नलिखित उदाहरण लें।
उदाहरण 9 निम्नलिखित आँकड़ों के लिए प्रसरण व मानक विचलन ज्ञात कीजिए:
| $x _{i}$ | 4 | 8 | 11 | 17 | 20 | 24 | 32 |
|---|---|---|---|---|---|---|---|
| $f _{i}$ | 3 | 5 | 9 | 5 | 4 | 3 | 1 |
हल आँकड़ों को सारणी के रूप में लिखने पर हमें निम्नलिखित सारणी 13.8 प्राप्त होती है:
सारणी 13.8
| $x _{i}$ | $f _{i}$ | $f _{i} x _{i}$ | $x _{i}-\bar{x}$ | $\left(x _{i}-\bar{x}\right)^{2}$ | $f _{i}\left(x _{i}-\bar{x}\right)^{2}$ |
|---|---|---|---|---|---|
| 4 | 3 | 12 | -10 | 100 | 300 |
| 8 | 5 | 40 | -6 | 36 | 180 |
| 11 | 9 | 99 | -3 | 9 | 81 |
| 17 | 5 | 85 | 3 | 9 | 45 |
| 20 | 4 | 80 | 6 | 36 | 144 |
| 24 | 3 | 72 | 10 | 100 | 300 |
| 32 | 1 | 32 | 18 | 324 | 324 |
| 30 | 420 | 1374 |
$ \begin{gathered} N=30, \sum\limits_ {i=1}^{7} f _ {i} x _ {i}=420, \sum\limits_ {i=1}^{7} f _ {i}(x _ {i}-\bar{x})^{2}=1374 \\ \text{अत}\quad \quad \quad \quad \bar{x}=\frac{\sum\limits_ {i=1}^{7} f _ {i} x _ {i}}{N}=\frac{1}{30} \times 420=14 \\ \text{अत }\quad \quad \quad \quad\text{ vपरसरण }(\sigma^{2})=\frac{1}{N} \sum\limits_ {i=1}^{7} f _ {i}(x _ {i}-\bar{x})^{2} \\ =\frac{1}{30} \times 1374=45.8 \end{gathered} $
$ \text{and }\quad \quad \quad \text{ मानक विचलन }(\sigma)=\sqrt{45.8}=6.77 $
13.5.3 एक सतत बारंबारता बंटन का मानक विचलन (Standard deviation of a continuous frequency distribution)
दिए गए सतत बारंबारता बंटन के सभी वर्गों के मध्य मान लेकर उसे असतत बारंबारता बंटन में निरूपित कर सकते हैं। तब असतत बारंबारता बंटन के लिए अपनाई गई विधि द्वारा मानक विचलन ज्ञात किया जाता है।
यदि एक $n$ वर्गों वाला बारंबारता बंटन जिसमें प्रत्येक अंतराल उसके मध्यमान $x _{i}$ तथा बारंबारता $f _{i}$, द्वारा परिभाषित किया गया है, तब मानक विचलन निम्नलिखित सूत्र द्वारा प्राप्त किया जाएगा:
$ \sigma=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{n} f_i(x_i-\bar{x})^{2}} $
जहाँ $\bar{x}$, बंटन का माध्य है और $\mathrm{N}=\sum _{i=1}^{n} f _{i}$.
मानक विचलन के लिए अन्य सूत्र हमें ज्ञात है कि
प्रसरण $ (\sigma^{2})=\frac{1}{N} \sum\limits_ {i=1}^{n} f _ {i}(x _ {i} \bar{x}) ^ {2} = \frac{1}{N} \sum\limits_{i = 1} ^ {n} f _ {i}(x _ i ^ {2} + \bar x ^{2} 2 \bar {x} x _ {i}) $
$ \begin{aligned} =\frac{1}{N}\begin{bmatrix} \sum\limits_ {i = 1} ^ {n} f _ {i} x _ i ^ {2} + \sum\limits_ {i = 1} ^ {n} \bar x ^{2} f_i-\sum\limits_{i=1}^{n} 2 \bar{x} f_i x_i\end{bmatrix}\end{aligned} $
$ \begin{aligned} & =\frac{1}{N}\begin{bmatrix}\sum\limits_ {i = 1} ^ {n} f _ {i} x _ i ^ {2} + \bar x ^ {2} \sum\limits_ {i = 1} ^ {n} f _ {i} 2 \bar{x} \sum\limits_ {i=1}^{n} x _{i} f _ {i} \end{bmatrix} \end{aligned} $
$ \begin{aligned} & =\frac {1}{N} \sum\limits_ {i = 1} ^ {n} f _ {i} x _ i ^ {2} + \bar x ^ {2} N 2 \bar{x} . N \bar{x} \quad[\text{ जहाँ } \frac {1}{N} \sum\limits_ {i = 1} ^ {n} x _ {i} f _ {i} = \bar{x} \text{ या } \sum\limits_ {i = 1} ^ {n} x _ {i} f _ {i}= N \bar{x}] \\ & =\frac {1}{N} \sum\limits_ {i = 1} ^ {n} f _ {i} x _ i ^ {2} + \bar x ^ {2} 2 \bar x ^ {2}=\frac {1}{N} \sum\limits_ {i = 1} ^ {n} f _ {i} x _ i ^ {2} \bar x^{2} \end{aligned} $
या
$ \sigma^{2}=\frac{1}{N} \sum\limits_{i=1}^{n} f_i x_i^{2}-\left(\frac{\sum\limits_{i=1}^{n} f_i x_i}{N}\right)^{2}=\frac{1}{N^{2}}\left[N \sum\limits_{i=1}^{n} f_i x_i^{2}-(\sum\limits_{i=1}^{n} f_i x_i)^{2}\right] $
अत: मानक विचलन $(\sigma)=\frac{1}{N} \sqrt{N \sum\limits_{i=1}^{n} f_i x_i{ }^{2}-(\sum\limits_{i=1}^{n} f_i x_i)^{2}}$
उदाहरण 10 निम्नलिखित बंटन के लिए माध्य, प्रसरण और मानक विचलन ज्ञात कीजिए:
| वर्ग | $30-40$ | $40-50$ | $50-60$ | $60-70$ | $70-80$ | $80-90$ | $90-100$ |
|---|---|---|---|---|---|---|---|
| बारंबारता | 3 | 7 | 12 | 15 | 8 | 3 | 2 |
हल दिए गए आँकड़ों से निम्नलिखित सारणी 13.9 बनाते हैं।
सारणी 13.9
| वर्ग | बारंबारता $\left(f _{i}\right)$ |
मध्य-बिंदु $\left(x _{i}\right)$ |
$f _{i} x _{i}$ | $\left(x _{i}-\bar{x}\right)^{2}$ | $f _{i}\left(x _{i}-\bar{x}\right)^{2}$ |
|---|---|---|---|---|---|
| $30-40$ | 3 | 35 | 105 | 729 | 2187 |
| $40-50$ | 7 | 45 | 315 | 289 | 2023 |
| $50-60$ | 12 | 55 | 660 | 49 | 588 |
| $60-70$ | 15 | 65 | 975 | 9 | 135 |
| $70-80$ | 8 | 75 | 600 | 169 | 1352 |
| $80-90$ | 3 | 85 | 255 | 529 | 1587 |
| $90-100$ | 2 | 95 | 190 | 1089 | 2178 |
| 50 | 3100 | 10050 |
अत: $ \quad \quad \quad \quad \text{ माध्य } \bar{x}=\frac{1}{N} \sum\limits_{i=1}^{7} f_i x_i=\frac{3100}{50}=62 $
प्रसरण $(\sigma^{2})=\frac{1}{N} \sum\limits_{i=1}^{7} f_i(x_i-\bar{x})^{2}$
$ =\frac{1}{50} \times 10050=201 $
और $ \quad \quad \quad \quad \text{ मानक विचलन }(\sigma)=\sqrt{201}=14.18 $
उदाहरण 11 निम्नलिखित आँकड़ों के लिए मानक विचलन ज्ञात कीजिए:
| $x _{i}$ | 3 | 8 | 13 | 18 | 23 |
|---|---|---|---|---|---|
| $f _{i}$ | 7 | 10 | 15 | 10 | 6 |
हल हम आँकड़ों से निम्नलिखित सारणी 13.10 बनाते हैं:
सारणी 13.10
| $x _{i}$ | $f _{i}$ | $f _{i} x _{i}$ | $x _{i}^{2}$ | $f _{i} x _{i}^{2}$ |
|---|---|---|---|---|
| 3 | 7 | 21 | 9 | 63 |
| 8 | 10 | 80 | 64 | 640 |
| 13 | 15 | 195 | 169 | 2535 |
| 18 | 10 | 180 | 324 | 3240 |
| 23 | 6 | 138 | 529 | 3174 |
| 48 | 614 | 9652 |
अब सूत्र (3) द्वारा
$ \begin{aligned} \sigma & =\frac{1}{N} \sqrt{N \sum{f_i x_i}^{2}-\left(\sum{f_i x_i}\right)^{2}} \\ \\ & =\frac{1}{48} \sqrt{48 \times 9652-(614)^{2}} \\ \\ & =\frac{1}{48} \sqrt{463296-376996} \end{aligned} $
$ =\frac{1}{48} \times 293.77=6.12 $
इसलिए, , $\quad$ मानक विचलन$(\sigma)=6.12$
13.5.4. प्रसरण व मानक विचलन ज्ञात करने के लिए लघु विधि (Shortcut method to find variance and standard deviation)
कभी-कभी एक बारंबारता बंटन के प्रेक्षणों $x _{i}$ अथवा विभिन्न वर्गों के मध्यमान $x _{i}$ के मान बहुत बड़े होते हैं तो माध्य तथा प्रसरण ज्ञात करना कठिन हो जाता है तथा अधिक समय लेता है। ऐसे बारंबारता बंटन, जिसमें वर्ग-अंतराल समान हों, के लिए पद विचलन विधि द्वारा इस प्रक्रिया को सरल बनाया जा सकता है।
मान लीजिए कि कल्पित माध्य ’ $A$ ’ है और मापक या पैमाने को $\frac{1}{h}$ गुना छोटा किया गया है (यहाँ $h$ वर्ग अंतराल है)। मान लें कि पद विचलन या नया चर $y _{i}$ है।
अर्थात् $\quad y_i=\frac{x_i-A}{h}$ or $x_i=A+h y_i \quad \quad \quad \quad \quad \ldots(1)$
हम जानते हैं कि $ \quad \quad \quad \bar{x}=\frac{\sum\limits_{i=1}^{n} f_i x_i}{N} \quad \quad \quad \quad \quad \ldots(2) $
(1) से $x _{i}$ को (2) में रखने पर हमें प्राप्त होता है
$ \begin{aligned} \bar{x} & =\frac{\sum\limits_{i=1}^{n} f_i(A+h y_i)}{N} \\ & =\frac{1}{N}(\sum\limits_{i=1}^{n} f_i A+\sum\limits_{i=1}^{n} h f_i y_i)=\frac{1}{N}(A \sum\limits_{i=1}^{n} f_i+h \sum\limits_{i=1}^{n} f_i y_i) \\ & =A \cdot \frac{N}{N}+h \frac{\sum\limits_{i=1}^{n} f_i y_i}{N} \quad(\text{ क्योंक } \sum\limits_{i=1}^{n} f_i=N) \end{aligned} $
अत: $\quad \bar{x}=A+h \bar{y} \quad \quad \quad\quad \quad \ldots(3)$
अब, चर $x$ का प्रसरण, $\sigma_x^{2}=\frac{1}{N} \sum\limits_{i=1}^{n} f_i(x_i-\bar{x})^{2}$
$ =\frac{1}{N} \sum\limits_{i=1}^{n} f_i(A+h y_i-A-h \bar{y})^{2} \quad \text{((1) और (3) द्वारा) } $
$ \begin{aligned} & =\frac{1}{N} \sum\limits_{i=1}^{n} f_i h^{2}(y_i-\bar{y})^{2} \\ & =\frac{h^{2}}{N} \sum\limits_{i=1}^{n} f_i(y_i-\bar{y})^{2}=h^{2} \times \text{ चर का प्रसरण } y_i \end{aligned} $
अर्थात् $\quad \sigma_x^{2}=h^{2} \sigma_y^{2}$
या $\quad \sigma_x=h \sigma_y \quad \quad \quad \quad \quad \ldots(4)$
(3) और (4), से हमें प्राप्त होता है कि
$ \sigma_x=\frac{h}{N} \sqrt{N \sum\limits_{i=1}^{n} f_i y_i^{2}-(\sum\limits_{i=1}^{n} f_i y_i)^{2}} \quad \quad \quad \quad \quad \ldots(5) $
आइए उदाहरण 11 के आँकड़ों में सूत्र (5) के उपयोग द्वारा लघु विधि से माध्य, प्रसरण व मानक विचलन ज्ञात करें।
उदाहरण 12 निम्नलिखित बंटन के लिए माध्य, प्रसरण व मानक विचलन ज्ञात कीजिए:
| वर्ग | $30-40$ | $40-50$ | $50-60$ | $60-70$ | $70-80$ | $80-90$ | $90-100$ |
|---|---|---|---|---|---|---|---|
| बारंबारता | 3 | 7 | 12 | 15 | 8 | 3 | 2 |
हल मान लें कल्पित माध्य $\mathrm{A}=65$ है। यहाँ $h=10$
दिए गए आँकड़ों से निम्नलिखित सारणी 13.11 प्राप्त होती है।
सारणी 13.11
| वर्ग | बारंबारत | मध्य-बिंदु | $y _{i}=\frac{x _{i}-65}{10}$ | $y _{i}{ }^{2}$ | $f _{i} y _{i}$ | $f _{i} y _{i}{ }^{2}$ |
|---|---|---|---|---|---|---|
| $f _{i}$ | $x _{i}$ | |||||
| $30-40$ | 3 | 35 | -3 | 9 | -9 | 27 |
| $40-50$ | 7 | 45 | -2 | 4 | -14 | 28 |
| $50-60$ | 12 | 55 | -1 | 1 | -12 | 12 |
| $60-70$ | 15 | 65 | 0 | 0 | 0 | 0 |
| $70-80$ | 8 | 75 | 1 | 1 | 8 | 8 |
| $80-90$ | 3 | 85 | 2 | 4 | 6 | 12 |
| $90-100$ | 2 | 95 | 3 | 9 | 6 | 18 |
| $\mathrm{N}=50$ | -15 | 105 |
इसलिए
$\quad \bar{x}=\mathrm{A}+\frac{\sum f _{i} y _{i}}{50} \times h=65-\frac{15}{50} \times 10=62$ $ \text { प्रसरण } \sigma^{2}=\frac{h^{2}}{\mathrm{~N}^{2}}\left[\mathrm{~N} \sum f _{i} y _{i}^{2}-\left(\sum f _{i} y _{i}\right)^{2}\right] $ $ \begin{aligned} & =\frac{(10)^{2}}{(50)^{2}}\left[50 \times 105-(-15)^{2}\right] \\ & =\frac{1}{25}[5250-225]=201 \end{aligned} $
और मानक विचलन $\sigma=\sqrt{201}=14.18$
प्रश्नावली 13.2
प्रश्न 1 से 5 तक के आँकड़ों के लिए माध्य व प्रसरण ज्ञात कीजिए।
1. $6,7,10,12,13,4,8,12$
Show Answer
\Missing2. प्रथम $n$ प्राकृत संख्याएँ
Show Answer
\Missing3. तीन के प्रथम 10 गुणज
Show Answer
\Missing4.
| $x _{i}$ | 6 | 10 | 14 | 18 | 24 | 28 | 30 |
|---|---|---|---|---|---|---|---|
| $f _{i}$ | 2 | 4 | 7 | 12 | 8 | 4 | 3 |
Show Answer
\Missing5.
| $x _{i}$ | 92 | 93 | 97 | 98 | 102 | 104 | 109 |
|---|---|---|---|---|---|---|---|
| $f _{i}$ | 3 | 2 | 3 | 2 | 6 | 3 | 3 |
Show Answer
\Missing6. लघु विधि द्वारा माध्य व मानक विचलन ज्ञात कीजिए।
| $x _{i}$ | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 |
|---|---|---|---|---|---|---|---|---|---|
| $f _{i}$ | 2 | 1 | 12 | 29 | 25 | 12 | 10 | 4 | 5 |
Show Answer
\Missingप्रश्न 7 व 8 में दिए गए बारंबारता बंटन के लिए माध्य व प्रसरण ज्ञात कीजिए।
7.
| वर्ग | $0-30$ | $30-60$ | $60-90$ | $90-120$ | $120-150$ | $150-180$ | $180-210$ |
|---|---|---|---|---|---|---|---|
| बारंबारता | 2 | 3 | 5 | 10 | 3 | 5 | 2 |
Show Answer
\Missing8.
| वर्ग | $0-10$ | $10-20$ | $20-30$ | $30-40$ | $40-50$ |
|---|---|---|---|---|---|
| बारंबारता | 5 | 8 | 15 | 16 | 6 |
Show Answer
\Missing9. लघु विधि द्वारा माध्य, प्रसरण व मानक विचलन ज्ञात कीजिए।
| ऊँचाई (सेमी में) |
$70-75$ | $75-80$ | $80-85$ | $85-90$ | $90-95$ | $95-100$ | $100-105$ | $105-110$ | $110-115$ |
|---|---|---|---|---|---|---|---|---|---|
| बच्चों की संख्या |
3 | 4 | 7 | 7 | 15 | 9 | 6 | 6 | 3 |
Show Answer
\Missing10. एक डिज़ाइन में बनाए गए वृत्तों के व्यास (मिमी में) नीचे दिए गए हैं।
| व्यास | $33-36$ | $37-40$ | $41-44$ | $45-48$ | $49-52$ |
|---|---|---|---|---|---|
| वृत्तों संख्या | 15 | 17 | 21 | 22 | 25 |
वृत्तों के व्यासों का मानक विचलन व माध्य व्यास ज्ञात कीजिए।
[संकेत पहले आँकड़ों को सतत बना लें। वर्गों को 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5-48.5, 48.5 52.5 लें और फिर आगे बढ़ें ]
Show Answer
\Missingविविध उदाहरण
उदाहरण 13 प्रेक्षणों का प्रसरण 5 है। यदि प्रत्येक प्रेक्षण को 2 से गुणा किया गया हो तो प्राप्त प्रेक्षणों का प्रसरण ज्ञात कीजिए।
हल मान लीजिए कि प्रेक्षण $x _{1}, x _{2}, \ldots, x _{20}$ और $\bar{x}$ उनका माध्य है। दिया गया है प्रसरण $=5$ और $n=20$. हम जानते हैं कि
$ \begin{aligned} & \text{ प्रसरण }(\sigma^{2})=\frac{1}{n} \sum\limits_{i=1}^{20}(x_i-\bar{x})^{2}, \text{ अर्थात्, } 5=\frac{1}{20} \sum\limits_{i=1}^{20}(x_i-\bar{x})^{2} \\ & \text{or}\quad \quad \quad \quad \sum\limits_{i=1}^{20}(x_i-\bar{x})^{2}=100 \end{aligned} $
यदि प्रत्येक प्रेक्षण को 2 से गुणा किया जाए, तो परिणामी प्रेक्षण $y _{i}$, हैं। स्पष्टतया
$ y_i=2 x_i \text{ अर्थात्, } x_i=\frac{1}{2} y_i \quad \quad \quad \quad \quad \quad \ldots(1) $
इसलिए $ \quad \quad \quad \quad\bar{y}=\frac{1}{n} \sum\limits_{i=1}^{20} y_i=\frac{1}{20} \sum\limits_{i=1}^{20} 2 x_i=2 \cdot \frac{1}{20} \sum\limits_{i=1}^{20} x_i $
अर्थात् $\quad \quad \quad \quad\bar{y}=2 \bar{x}$ या $\bar{x}=\frac{1}{2} \bar{y}$
$x _{i}$ और $\bar{x}$ के मान (1) में प्रतिस्थापित करने पर हमें प्राप्त होता है।
$ \sum _{i=1}^{20} \frac{1}{2} y _{i}-\frac{1}{2} \bar{y}^{2}=100, \text { अर्थात् } \sum _{i=1}^{20}\left(y _{i}-\bar{y}\right)^{2}=400 $
अतः नए प्रेक्षणों का प्रसरण $=\frac{1}{20} \times 400=20=2^{2} \times 5$
टिप्पणी पाठक ध्यान दें कि यदि प्रत्येक प्रेक्षण को $k$, से गुणा किया जाए, तो नए बने प्रेक्षणों का प्रसरण, पूर्व प्रसरण का $k^{2}$ गुना हो जाता है।
उदाहरण 14 पाँच प्रेक्षणों का माध्य 4.4 है तथा उनका प्रसरण 8.24 है। यदि तीन प्रेक्षण 1,2 तथा 6 हैं, तो अन्य दो प्रेक्षण ज्ञात कीजिए।
हल माना शेष दो प्रेक्षण $x$ तथा $y$ हैं।
इसलिए, शृंखला $1,2,6, x, y$ है।
अब, $ \quad \quad \quad \quad\text{माध्य} \bar{x}=4.4=\frac{1+2+6+x+y}{5} $
या $ \quad \quad \quad \quad 22=9+x+y $
इसलिए $\quad x+y=13\quad \quad \quad \quad\quad \quad \ldots(1)$
साथ ही $\quad$ प्रसरण $=8.24=\frac{1}{n} \sum\limits_{i=1}^{5}(x_i-\bar{x})^{2}$
अर्थात् $8.24=\frac{1}{5}\left[(3.4)^{2}+(2.4)^{2}+(1.6)^{2}+x^{2}+y^{2}-2 \times 4.4(x+y)+2 \times(4.4)^{2}\right]$
या $\quad 41.20=11.56+5.76+2.56+x^{2}+y^{2}-8.8 \times 13+38.72$
इसलिए $\quad x^{2}+y^{2}=97\quad \quad \quad \quad\quad \quad \ldots(2)$
लेकिन (1) से, हमें प्राप्त होता है
$ x^{2}+y^{2}+2 x y=169 \quad \quad \quad \quad\quad \quad \ldots(3) $
(2) और (3), से हमें प्राप्त होता है
$ 2 x y=72 \quad \quad \quad \quad\quad \quad \ldots(4) $
(2) में से (4), घटाने पर,
$ \begin{aligned} & x^{2}+y^{2}-2 x y=97-72 \quad \text{ अर्थात् } \quad (x-y)^{2}=25 \\ & \text{या} \quad \quad \quad x-y= \pm 5 \quad \quad \quad \quad\quad \quad \ldots(5) \end{aligned} $
अब (1) और (5) से, हमें प्राप्त होता है
$ x=9, y=4 \text{ जब } x-y=5 $ या $\quad x=4, y=9$ जब $x-y=-5$
अतः शेष दो प्रेक्षण 4 तथा 9 हैं।
उदाहरण 15 यदि प्रत्येक प्रेक्षण $x _{1}, x _{2}, \ldots, x _{n}$ को ’ $a$ ‘, से बढ़ाया जाए जहाँ $a$ एक ऋणात्मक या धनात्मक संख्या है, तो दिखाइए कि प्रसरण अपरिवर्तित रहेगा।
हल मान लें प्रेक्षण $x _{1}, x _{2}, \ldots, x _{n}$ का माध्य $\bar{x}$ है, तो उनका प्रसरण
$ \sigma _{1}^{2}=\frac{1}{n} \sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2} \text { द्वारा दिया जाता है। } $
यदि प्रत्येक प्रेक्षण में $a$ जोड़ा जाए तो नए प्रेक्षण होंगे
$ \begin{equation*} y _{i}=x _{i}+a \tag{1} \end{equation*} $
मान लीजिए नए प्रेक्षणों का माध्य $\bar{y}$ है तब
$ \begin{aligned} \bar{y} & =\frac{1}{n} \sum\limits_{i=1}^{n} y_i=\frac{1}{n} \sum\limits_{i=1}^{n}(x_i+a) \\ & =\frac{1}{n}[\sum\limits_{i=1}^{n} x_i+\sum\limits_{i=1}^{n} a]=\frac{1}{n} \sum\limits_{i=1}^{n} x_i+\frac{n a}{n}=\bar{x}+a \end{aligned} $
अर्थात् $ \quad \quad \quad \bar{y}=\bar{x}+a \quad \quad \quad \quad\quad \quad \ldots(1) $
अतः नए प्रेक्षणों का प्रसरण
$ \begin{aligned} \sigma _{2}^{2} & =\frac{1}{n} \sum _{i=1}^{n}\left(y _{i}-\bar{y}\right)^{2}=\frac{1}{n} \sum _{i=1}^{n}\left(x _{i}+a-\bar{x}-a\right)^{2} \quad((1) \text { और }(2) \text { के उपयोग से) } \\ & =\frac{1}{n} \sum _{i=1}^{n}\left(x _{i}-\bar{x}\right)^{2}=\sigma _{1}^{2} \end{aligned} $
अतः नए प्रेक्षणों का प्रसरण वही है जो मूल प्रेक्षणों का था।
टिप्पणी ध्यान दीजिए कि प्रेक्षणों के किसी समूह में प्रत्येक प्रेक्षण में कोई एक संख्या जोड़ने अथवा घटाने पर प्रसरण अपरिवर्तित रहता है।
उदाहरण 16 एक विद्यार्थी ने 100 प्रेक्षणों का माध्य 40 और मानक विचलन 5.1 ज्ञात किया, जबकि उसने गलती से प्रेक्षण 40 के स्थान पर 50 ले लिया था। सही माध्य और मानक विचलन क्या है?
हल दिया है, प्रेक्षणों की संख्या $(n)=100$
गलत माध्य $(\bar{x})=40$,
गलत मानक विचलन $(\sigma)=5.1$
हम जानते हैं कि $\bar{x}=\frac{1}{n} \sum\limits_{i=1}^{n} x_i$
अर्थात् $ \quad \quad \quad 40=\frac{1}{100} \sum\limits_{i=1}^{100} x_i \quad \text{ or } \quad \sum\limits_{i=1}^{100} x_i=4000 $
अर्थात् $\quad$ प्रेक्षणों का गलत योग $=4000$
अत: $\quad \quad \quad$प्रेक्षणों का सही योग $=$ गलत योग $-50+40$
$ =4000-50+40=3990 $
इसलिए $\quad$ $ \text { सही माध्य }=\frac{\text { सही योग }}{100}=\frac{3990}{100}=39.9 $
साथ ही $\quad$ मानक विचलन $\sigma=\sqrt{\frac{1}{n} \sum _{i=1}^{n} x _{i}{ }^{2}-\frac{1}{n^{2}}\left(\sum _{i=1}^{n} x _{i}\right)^{2}}$
$ =\sqrt{\frac{1}{n} \sum _{i=1}^{n} x _{i}^{2}-(\bar{x})^{2}} $
अर्थात् $ \quad \quad \quad\quad \quad \quad 5.1=\sqrt{\frac{1}{100} \times गलत \sum\limits_{i=1}^{n} x_i^{2}-(40)^{2}}$
या $ \quad \quad \quad\quad \quad \quad 26.01=\frac{1}{100} \times \text{ गलत } \sum\limits_{i=1}^{n} x_i^{2}-1600 $
इसलिए $\quad$ $ \text { गलत } \sum _{i=1}^{n} x _{i}^{2}=100(26.01+1600)=162601 $
अब $\quad \quad \quad\quad \quad \quad$ सही $\sum\limits_{i=1}^{n} x_i^{2}=$ गलत $\sum\limits_{i=1}^{n} x_i{ }^{2}-(50)^{2}+(40)^{2}$
$ =162601-2500+1600=161701 $
इसलिए सही मानक विचलन
$ \begin{aligned} & =\sqrt{\frac{\text{ सही } \sum x_i^{2}}{n}-(\text{ सही माध्य })^{2}} \\ & =\sqrt{\frac{161701}{100}-(39.9)^{2}} \\ & =\sqrt{1617.01-1592.01}=\sqrt{25}=5 \\ \end{aligned} $
अध्याय 13 पर विविध प्रश्नावली
1. आठ प्रेक्षणों का माध्य तथा प्रसरण क्रमशः 9 और 9.25 हैं। यदि इनमें से छः प्रेक्षण $6,7,10$, 12,12 और 13 हैं, तो शेष दो प्रेक्षण ज्ञात कीजिए।
Show Answer
\missing2. सात प्रेक्षणों का माध्य तथा प्रसरण क्रमश: 8 तथा 16 हैं। यदि इनमें से पाँच प्रेक्षण $2,4,10$, 12,14 हैं तो शेष दो प्रेक्षण ज्ञात कीजिए।
Show Answer
\missing3. छः प्रेक्षणों का माध्य तथा मानक विचलन क्रमशः 8 तथा 4 हैं। यदि प्रत्येक प्रेक्षण को तीन से गुणा कर दिया जाए तो परिणामी प्रेक्षणों का माध्य व मानक विचलन ज्ञात कीजिए।
Show Answer
\missing4. यदि $n$ प्रेक्षणों $x _{1}, x _{2}, \ldots, x _{n}$ का माध्य $\bar{x}$ तथा प्रसरण $\sigma^{2}$ हैं तो सिद्ध कीजिए कि प्रेक्षणों $a x _{1}$, $a x _{2}, a x _{3}, \ldots, a x _{n}$ का माध्य और प्रसरण क्रमशः $a \bar{x}$ तथा $a^{2} \sigma^{2}(a \neq 0)$ हैं।
Show Answer
\missing5. बीस प्रेक्षणों का माध्य तथा मानक विचलन क्रमशः 10 तथा 2 हैं। जाँच करने पर यह पाया गया कि प्रेक्षण 8 गलत है। निम्न में से प्रत्येक का सही माध्य तथा मानक विचलन ज्ञात कीजिए यदि
(i) गलत प्रेक्षण हटा दिया जाए।
(ii) उसे 12 से बदल दिया जाए।
Show Answer
\missing6. 100 प्रेक्षणों का माध्य और मानक विचलन क्रमशः 20 और 3 हैं। बाद में यह पाया गया कि तीन प्रेक्षण 21,21 तथा 18 गलत थे। यदि गलत प्रेक्षणों को हटा दिया जाए तो माध्य व मानक विचलन ज्ञात कीजिए।
Show Answer
\missingसारांश
प्रकीर्णन की माप आँकड़ों में बिखराव या विचरण की माप। परिसर, चतुर्थक विचलन, माध्य विचलन व मानक विचलन प्रकीर्णन की माप हैं।
परिसर $=$ अधिकतम मूल्य न्यूनतम मूल्य
अवर्गीकृत आँकड़ों का माध्य विचलन
M.D. $(\bar{x})=\frac{\sum|x_i-\bar{x}|}{n}, \quad$ M.D. $(M)=\frac{\sum|x_i-M|}{n}$ जहाँ $\bar{x}=$ माध्य और $\mathrm{M}=$ माध्यिका
वर्गीकृत आँकड़ों का माध्य विचलन
M.D. $(\bar{x})=\frac{\sum f_i|x_i \quad \bar{x}|}{N}, \quad$ M.D. (M) $=\frac{\sum f_i \mid x_i}{N}$ M , जहाँ $N=\sum f_i$
अवर्गीकृत आँकड़ों का प्रसरण और मानक विचलन
$\sigma^{2}=\frac{1}{n} \sum(x_i-\bar{x})^{2}, \quad \sigma=\sqrt{\frac{1}{n} \sum(x_i-\bar{x})^{2}}$
असतत बारंबारता बंटन का प्रसरण तथा मानक विचलन
$ \sigma^{2}=\frac{1}{N} \sum f_i(x_i-\bar{x})^{2}, \quad \sigma=\sqrt{\frac{1}{N} \sum f_i(x_i-\bar{x})^{2}} $
सतत बारंबारता बंटन का प्रसरण तथा मानक विचलन
$ \sigma^{2}=\frac{1}{N} \sum f_i(x_i-\bar{x})^{2}, \quad \sigma=\frac{1}{N} \sqrt{N \sum f_i x_i^{2}-(\sum f_i x_i)^{2}} $
प्रसरण और मानक विचलन ज्ञात करने की लघु विधि
$ \begin{aligned} & \sigma^{2}=\frac{h^{2}}{N^{2}}[N \sum f_i y_i^{2}-(\sum f_i y_i)^{2}], \sigma=\frac{h}{N} \sqrt{N \sum f_i y_i^{2}-(\sum f_i y_i)^{2}}, \\ \\ & \text{ जहाँ } y_i=\frac{x_i-A}{h} \end{aligned} $
ऐतिहासिक पृष्ठभूमि
सांख्यिकी का उद्भव लैटिन शब्द ‘status’ से हुआ है जिसका अर्थ एक राजनैतिक राज्य होता है। इससे पता लगता है कि सांख्यिकी मानव सभ्यता जितनी पुरानी है। शायद वर्ष 3050 ई.पू. में यूनान में पहली जनगणना की गई थी। भारत में भी लगभग 2000 वर्ष पहले प्रशासनिक आँकड़े एकत्रित करने की कुशल प्रणाली थी। विशेषतः चंद्रगुप्त मौर्य (324-300 ई.पू.) के राज्य काल में कौटिल्य (लगभग 300 ई.पू.) के अर्थशास्त्र में जन्म और मृत्यु के आँकड़े एकत्रित करने की प्रणाली का उल्लेख मिला है। अकबर के शासनकाल में किए गये प्रशासनिक सर्वेक्षणों का वर्णन अबुलफज़ल द्वारा लिखित पुस्तक आइने-अकबरी मे दिया गया है।
लंदन के केप्टन John Graunt (1620-1675) को उनके द्वारा जन्म और मृत्यु की सांख्यिकी के अध्ययन के कारण उन्हें जन्म और मृत्यु सांख्यिकी का जनक माना जाता है। Jacob Bernoulli (1654-1705) ने 1713 मे प्रकाशित अपनी पुस्तक Ars Conjectandi में बड़ी संख्याओं के नियम को लिखा है।
सांख्यिकी का सैद्धांतिक विकास सत्रहवीं शताब्दी के दौरान खेलों और संयोग घटना के सिद्धांत के परिचय के साथ हुआ तथा इसके आगे भी विकास जारी रहा। एक अंग्रेज़ Francis Galton (1822-1921) ने जीव सांख्यिकी (Biometry) के क्षेत्र में सांख्यिकी विधियों के उपयोग का मार्ग प्रशस्त किया। Karl Pearson (1857-1936) ने काई वर्ग परीक्षण (Chi square test) तथा इंग्लैंड में सांख्यिकी प्रयोगशाला की स्थापना के साथ सांख्यिकीय अध्ययन के विकास में बहुत योगदान दिया है। Sir Ronald a. Fisher (1890-1962) जिन्हें आधुनिक सांख्यिकी का जनक माना जाता है, ने इसे विभिन्न क्षेत्रों जैसे अनुवांशिकी, जीव-सांख्यिकी, शिक्षा, कृषि आदि में लगाया।





