Conic Sections का हिंदी में अनुवाद क्या होगा?
अध्याय 11
कोनिक खंड
11.1 अवलोकन
11.1.1 कोन के खंड एक निश्चित ऊर्ध्वतालीय रेखा $l$ और एक दूसरी रेखा $m$ की गठन की एक निश्चित बिन्दु $V$ पर केंद्रित होकर इसे एक आयताकार दोहनित सही वृत्त खोखले कोन (कोन) कहलाते हैं और इसकी ऊर्ध्वचाप में असीमित रूप से विस्तार होती हैं (चित्र 11.1).
चित्र 11.1
सोचें कि हम रेखा $m$ को रेखा $l$ के चारों ओर एक ऐसे तरीके से घुमाते हैं कि कोन $\alpha$ निरंतर रहते हैं। तब उत्पन्न सत्रीय तीक्ष्ण कोन की सतह एक दोहरी झूलती हुई सही वृत्त खोखली होती है, जिसे इसके बाद दोनों दिशाओं में असीमित रूप से विस्तारित किया जाता है (चित्र 11.2).
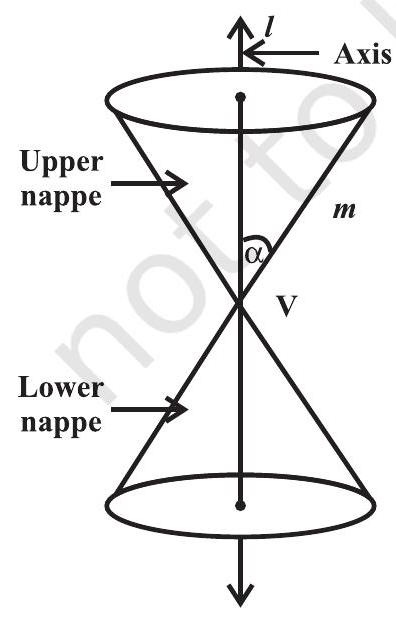
चित्र 11.2
चित्र 11.3
बिंदु $V$ को शिर्षक कहा जाता है; रेखा $l$ को कोन का अक्ष कहा जाता है। घुराने वाली रेखा $m$ को कोन का उत्पादक कहा जाता है। शिर्षक कोन को दो भागों में विभाजित करता है, जिसे खंड कहते हैं।
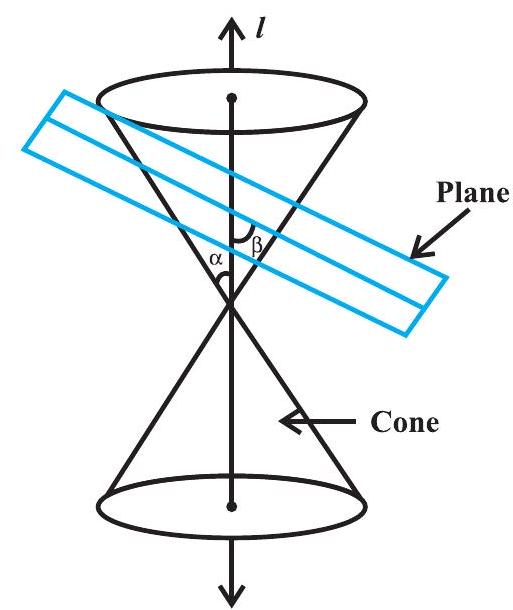
यदि हम एक तल और एक कोन के साथ एक तल को मिलाएं, तो प्राप्त संख्या कोनिक खंड कहते हैं। इस प्रकार, तल कोन को एक समरेखा गोलीय कोन पर सापेक्ष करने से प्राप्त किया जाता है।
हम निर्माण के समरेखा के स्थान पर निर्भरता और यांत्रिक ध्यान धारित करने वाली कोन के लंबवत अक्ष के साथ बनाने वाले कोनिक खंड प्राप्त करते हैं। चित्र 11.3 में तल द्वारा किए गए खंड के उभरते भाग निश्चित कर रही हैं।
तल (शिर्षक को छोड़कर) के कोन को कटता है, हमारे पास निम्नलिखित स्थितियां होती हैं:
(a) जब $\beta=90^{\circ}$ हो, तो खंड एक वृत्त होता है।
(b) जब $\alpha<\beta<90^{\circ}$ हो, तो खंड एक अंडाकारिय होता है।
(c) जब $\beta=\alpha$ हो; तो खंड एक पराबोला होता है।
(इन तीन स्थितियों में प्रत्येक में, तल कोन के एक खंड में पूर्णतया पारित होता है।)
(d) जब $0 \leq \beta<\alpha$ हो; तो तल को दो भागों और संबद्धता की क्लिरव का अंश होता है।
वास्तव में, ये खंड आउटर स्थानिक प्रवेश और परमाणु कणों के व्यवहार के अनुसंधान में महत्वपूर्ण उपकरण हैं।
हम कोनिक खंडों को आयताकार कृष्ण तरंगों के रूप में लेते हैं। इस उद्देश्य के लिए, यह सुविधाजनक होता है कि हम उस प्लेन का ही उपयोग करें जिसमें कोण पर विचार कर रहा है, और इस प्लेन में स्पष्ट बिंदुओं और रेखाओं पर उल्लेख हो, जिन्हें केंद्र बिंदु और उग्र संकेतक नामकित किया जाता है। इस दृष्टिकोण से, पराबोला, अंडाकारिया और क्षेत्रफल कहलाते हैं जो यथार्थ में तल में एक निश्चित बिंदु (उत्केंद्र) और निश्चित रेखा (अवतरणी) में परिभाषित होते हैं।
यदि $S$ फोकस है और $l$ निर्देशांक है, तो उन सभी बिंदुओं का सेट जो विमुखता के बारे में एक स्थिर अनुपात $e$ के लिए जो उनकी दूरी $l$ से होती है, वह एक पत्र्रक के रूप में है।
एलिप्स के विशेष मामले के रूप में, हम $e=0$ के लिए वृत्त प्राप्त करते हैं और इसलिए हम इसे अलग तरीके से अध्ययन करते हैं।
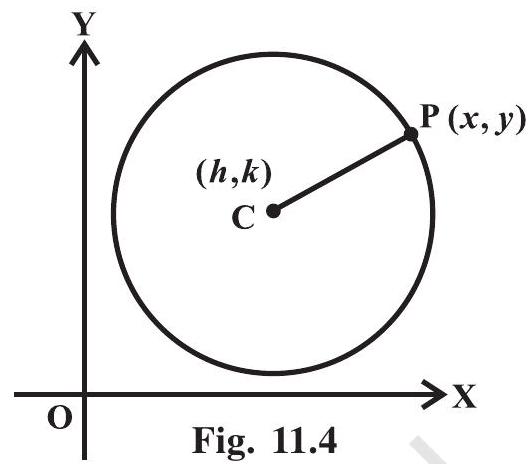
11.1.2 वृत्त एक तच्ची प्लेन में उन सभी बिंदुओं का सेट है जो मूल्य नगरीया नगरीया नगरीया बिंदु से एक निर्दिष्ट दूरी पर हैं। मूल्य नगरीया नगरीया नगरीया बिंदु को केंद्र कहा जाता है और वृत्त पर केंद्र से कोई भी बिंदु तक की दूरी को वृत्त का त्रिज्या कहा जाता है।
रेडियस $r$ और केंद्र $(h, k)$ वाले वृत्त की समीकरण दी गई है $(x-h)^{2}+(y-k)^{2}=r^{2}$ वृत्त की सामान्य समीकरण दी गई है $x^{2}+y^{2}+2 g x+2 f y+c=0$, जहां $g, f$ और $c$ स्थिरांक हैं।
(a) इस वृत्त का केंद्र $(-g,-f)$ है
(b) वृत्त का त्रिज्या $\sqrt{g^{2}+f^{2}-c}$ है
सन्दर्भ में के माध्यम से 0 याने की दूरी से बहुत कम है।
(c) प्रायिकता का सामान्य समीकरण $x^{2}+y^{2}+2 g x+2 f y=0$ है।
दूसरी डिग्री की सामान्य समीकरण, अर्थात $a x^{2}+2 h x y+b y^{2}+2 g x+2 f y+c=0$ एक वृत्त को प्रतिष्ठान करती है यदि (i) $x^{2}$ के संकेतक और $y^{2}$ के समांक का समांक बराबर होता है, अर्थात $a=b \neq 0$ और (ii) $x y$ का सदिश सूत्र शून्य होता है, अर्थात $h=0$।
वृत्त की पैरामीट्रिक समीकरणें $x^{2}+y^{2}=r^{2}$ द्वारा दी जाती हैं $x=r \cos \theta, y=r \sin \theta$ जहां $\theta$ मास्क है और $x=h+r \cos \theta, y=k+r \sin \theta$ हैं।
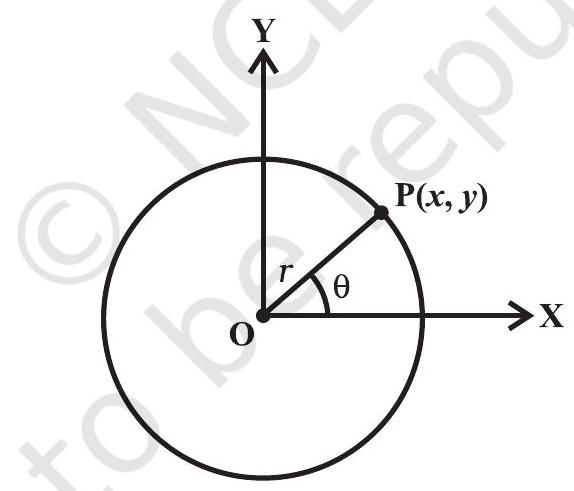
एक विस्तृत देखें।
ध्यान दें: वृत्त का सामान्य समीकरण तीन सांकेतिक होता है जो इसका मतलब है कि कम से कम तीन स्थितियाँ एकदृश्य आकार को निर्धारित करने के लिए आवश्यक हैं।
11.1.3 पाराबोला
एक पाराबोला वह सभी बिंदुओं का सेट है जिनकी दूरी प्लेन में एक स्थिर बिंदु $F$ से उनकी दूरी एक स्थिर रेखा $l$ से बराबर होती है। एक प्राइमेक विमुखता और निर्देश लेख方।
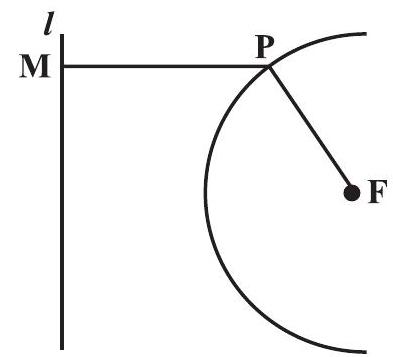
एक पराबोला के मानक समीकरणों की स्थानिक समरूपताएं नीचे दिखाई गई हैं।
११.३.ट्रिशूल
प्रायिकता जो $F$ एक सदॊजज कोण मे निर्दिष्ट नगरीया लौ\u0301ती है जिसकी बंनान आधार परिधि का अक्ष को एक संदॊजज पराबोला कहा जाता है, तथा जिसका आधारी सरणी एक गठ है, जबकि दोनो संदॊजे पराबोलों की मानक छवि नीचे दिखायी गयी है।
कंटेन्ट का हिंदी संस्करण:
(b)
(डी)
चित्र 11.7
पराबोला के मुख्य तथ्य
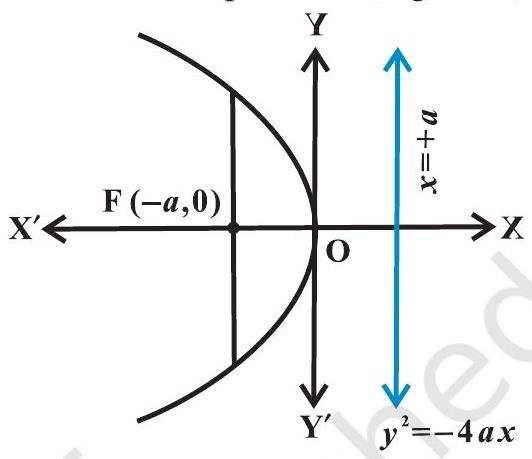
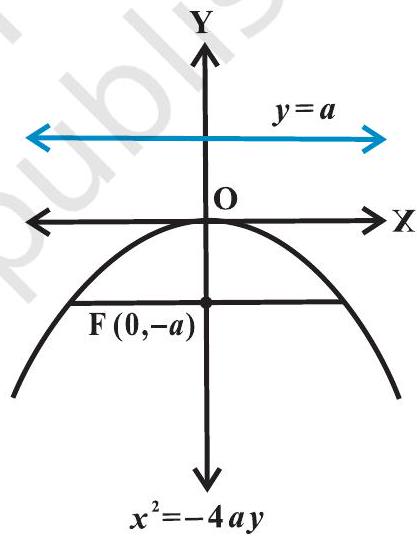
| पराबोले की रूपांतरणों | $y^{2}=4 a x$ | $y^{2}=-4 a x$ | $x^{2}=4 a y$ | $x^{2}=-4 a y$ |
|---|---|---|---|---|
| धुरी | $y=0$ | $y=0$ | $x=0$ | $x=0$ |
| अभिनिर्देश | $x=-a$ | $x=a$ | $y=-a$ | $y=a$ |
| शिरषक | $(0,0)$ | $(0,0)$ | $(0,0)$ | $(0,0)$ |
| फोकस | $(a, 0)$ | $(-a, 0)$ | $(0, a)$ | $(0,-a)$ |
| लंबी औरत की लंबाई | $4 a$ | $4 a$ | $4 a$ | $4 a$ |
| लंबी औरत का समीकरण | $x=a$ | $x=-a$ | $y=a$ | $y=-a$ |
एक बिंदु की फोकस दूरी
अगर पराबोले की समीकरण हो $y^{2}=4 a x$ और $P(x, y)$ उस पर हो एक बिंदु. तो यहां उस बिंदु से पॉइंट $P$ तक की दूरी, जिसे फोकस दूरी कहा जाता है, है, अर्थात्,
$ \begin{aligned} FP & =\sqrt{(x-a)^{2}+y^{2}} \\ & =\sqrt{(x-a)^{2}+4 a x} \\ & =\sqrt{(x+a)^{2}} \\ & =|x+a| \end{aligned} $
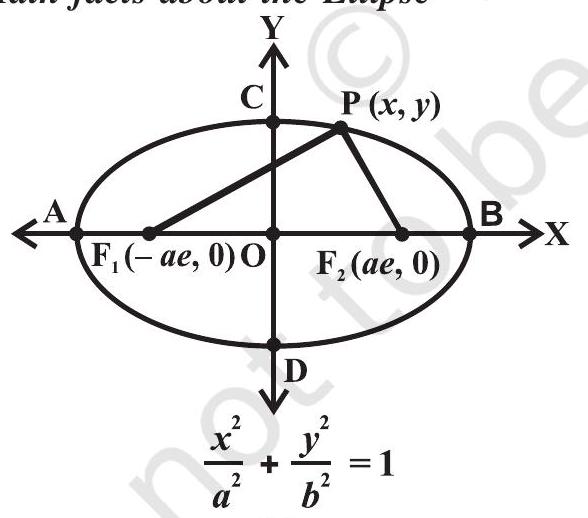
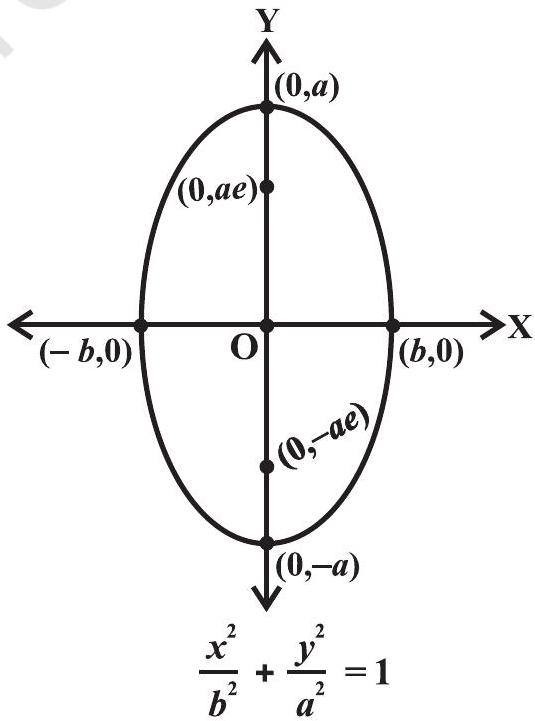
11.1.4 अंडाकार अंडाकार एक समतल में एक बिंदु से दो निश्चित बिंदुओं तक की दूरी की संख्या है, जो स्थिर है। या, अंडाकार वह सभी बिंदुओं का सेट है जो स्थिर बिन्दु से एक निश्चित आंतरिक अनुपात से, एक स्थिर रेखा से उनकी दूरी से घटकर, प्लेन में है। निश्चित बिंदु के बारे में कहा जाता है, फोकस, स्थिर रेखा एक सीधी रेखा है और निश्चित अनुपात ( $e$ ) एंडाकार की ऊँचाई है।
एंडाकार के दो मानक रूप हैं, अर्थात्
(i) $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \quad$ और $\quad$ (ii) $\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$,
दोनों मामलों में $a>b$ और $b^{2}=a^{2}(1-e^{2}), e<1$ है।
(i) मेजर धुरी $x$-axis के साथ है और माइनर $y$-axis के साथ है और (ii) मेजर धुरी $y$-axis के साथ है और माइनर $x$ -अक्ष के साथ है, जैसा कि चित्र 11.8 (a) और (b) में दिखाया गया है।
अंडाकार के मुख्य तथ्य
(a)
(b)
चित्र 11.8
| अंडाकार के रूप | $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ | $\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$ |
|---|---|---|
| माजर धुरी की समीकरण | $a>b$ | $a>b$ |
| माजर धुरी की लंबाई | $y=0$ | $x=0$ |
| माइनर धुरी की समीकरण | $x=0$ | $2 a$ |
| माइनर धुरी की लंबाई | $2 b$ | $y=0$ |
| अभिनिर्देश | $x= \pm \frac{a}{e}$ | $y= \pm \frac{a}{e}$ |
| लंबी औरत की समीकरण | $x= \pm a e$ | $y= \pm a e$ |
| लंबी औरत की लंबाई | $\frac{2 b^{2}}{a}$ | $\frac{2 b^{2}}{a}$ |
| केंद्र | $(0,0)$ | $(0,0)$ |
फोकस दूरी
अंडाकार $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ पर एक बिंदु $(x, y)$ की फोकस दूरी है
$ \begin{aligned} & a-e|x| \text{ के पास से} \\
दूर केंद्र से किसी भी बिंदु $(x, y)$ का फ़ोकसी दूरी हाइपरबोला $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ पर
नजदीकी फोकस से $e|x|-a$
दूर फोकस से $e|x|+a$
दूरी साथ किसी भी बिन्दु की फोकसी की फ़ोकस तथांक के अंतर के बराबर होती है और तार्किक ध्विमाक्ष की लंबाई के बराबर होती है।
~~उदाहरण 2 यदि पराबोला का समीकरण $x^{2}=-8 y$ हो, तो फोकस के संदर्भ में स्थानांतरण करें, सीधी रेखा का समीकरण और ऊचाई वृत्तक की लंबाई।
समाधान दिए गए समीकरण का प्रारूप है $x^{2}=-4 a y$ जहां $a$ सकारात्मक है।
इसलिए, फोकस $y$-अक्ष पर नकारात्मक दिशा में होता है और पराबोला नीचे की ओर खुलता है।
मानक रूप के दिए गए समीकरण की तुलना करने से, हमें $a=2$ मिलता है।
इसलिए, फोकस के संदर्भ मान $(0,-2)$ हैं और सीधी रेखा का समीकरण $y=2$ है और लंबाई वृत्तक की लंबाई $4 a$, अर्थात 8 है।
~~उदाहरण 3 समीकरण $9 x^{2}+25 y^{2}=225$ वाले तिर्भुज के मुख्य और गुणवत्ता, धनात्मकता, फोकस और मूल्यांकन ढूंढें।
समाधान हम $225$ से विभाजित करके सामान्य रूप में समीकरण रखते हैं और प्राप्त करते हैं
$ \frac{x^{2}}{25}+\frac{y^{2}}{9}=1 $
इससे हमें $a=5$ और $b=3$ मिलता है। इसलिए $9=25(1-e^{2})$, तो $e=\frac{4}{5}$ होता है। $x^{2}$ के नामकारक बड़ा होने की वजह से, मुख्य धनात्मक या-अक्ष है, छोटा या-अक्ष है, फोकस $(4,0)$ और $(-4,0)$ हैं और मूल्यांकन $(5,0)$ और $(-5,0)$ हैं।
~~उदाहरण 4 फोकस $( \pm 5,0)$ और $x=\frac{36}{5}$ एक सीधी वाला अधिकारियों का समीकरण खोजें।
समाधान हमें $a e=5, \frac{a}{e}=\frac{36}{5}$ होता है जो $a^{2}=36$ या $a=6$ देता है। इसलिए, $e=\frac{5}{6}$ होता है।
अब $b=a \sqrt{1-e^{2}}=6 \sqrt{1-\frac{25}{36}}=\sqrt{11}$। इस तरह, तिर्भुज का समीकरण $\frac{x^{2}}{36}+\frac{y^{2}}{11}=1$ होता है।
~~उदाहरण 5 तिर्भुज $9 x^{2}-16 y^{2}=144$ के मूल्यांकन, फोकस और गुणवत्ता ढूंढें।
समाधान तिर्भुज का समीकरण $\frac{x^{2}}{16}-\frac{y^{2}}{9}=1$ के रूप में लिखा जा सकता है, इसलिए $a=4, b=3$ और $9=16(e^{2}-1)$, इसलिए $e^{2}=\frac{9}{16}+1=\frac{25}{16}$ होता है, जो $e=\frac{5}{4}$ देता है। मूल्यांकन $( \pm a, 0)=$ $( \pm 4,0)$ होते हैं और फोकस $( \pm a e, 0)=( \pm 5,0)$ होते हैं।
~~उदाहरण 6 जिसके मूल्यांकन $(0, \pm 6)$ हैं और $e=\frac{5}{3}$ है, उस तिर्भुज का समीकरण खोजें। अपने फोकस ढूंढें।
समाधान मूल्यांकन $y$-अक्ष पर होने के कारण (मध्यबिंदु के साथ मूल्यांकन), समीकरण $\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1$ का होता है।
मूल्यांकन $(0, \pm 6), a=6, b^{2}=a^{2}(e^{2}-1)=36 \quad \frac{25}{9}-1=64$ होता है, इसलिए तिर्भुज का आवश्यक समीकरण $\frac{y^{2}}{36}-\frac{x^{2}}{64}=1$ होता है और फोकस $(0, \pm a e)=(0, \pm 10)$ होते हैं।
लंबे उत्तर प्रकार
~~उदाहरण 7 सर्कल जिससे बिंदु $(20,3)$, $(19,8)$ और $(2,-9)$ से गुजरता है, का समीकरण खोजें। उसका केंद्र और अर्धव्यास ढूंढें।
समाधान सर्कल के सामान्य समीकरण $x^{2}+y^{2}+2 g x+2 f y+c=0$ में सदिशों को स्थानांतरित करके, हमें निम्नलिखित मिलता है
$ \begin{aligned} 40 g+6 f+c & =-409 \\ 38 g+16 f+c & =-425 \\ 4 g-18 f+c & =-85 \end{aligned} $
इन तीन समीकरणों से, हमें
$g=-7, f=-3$ और $c=-111$ मिलता है।
इसलिए, सर्कल का समीकरण होता है
$x^{2}+y^{2}-14 x-6 y-111=0$ या $(x-7)^{2}+(y-3)^{2}=13^{2}$।
इसलिए, सर्कल का केंद्र $(7,3)$ है और अर्धव्यास 13 है।
उदाहरण 8 एक समानाधिबहुज त्रिभुज परत $y^{2}=4 a x$ में समांतरांकित किया जाता है जिसका एक कोण परत का अकर्ण होता है। त्रिभुज की पक्ष की लंबाई ढूंढें।
समाधान जैसा चित्र में दिखाया गया है, APQ समानार्धी त्रिभुज है जिसमें l (उम्मीद है) इसकी समान पक्ष है।
यहां
और,
इसलिए $\frac{l \sqrt{3}}{2}, \frac{l}{2}$ नक़्शा $y^{2}=4 a x$ पर स्थित बिंदु $P$ की आवधारणिक निर्देशांक हैं।
$ \begin{aligned} AP & =l इसलिए AR=l \cos 30^{\circ} \\ & =l \frac{\sqrt{3}}{2} \end{aligned} $
$ PR=l \sin 30^{\circ}=\frac{l}{2} . $
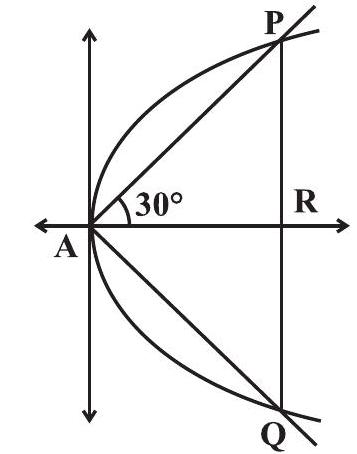
चित्र 11.10
इसलिए,
$ \frac{l^{2}}{4}=4 a \frac{l \sqrt{3}}{2} \Rightarrow l=8 a \sqrt{3} . $
इस प्रकार, $8 a \sqrt{3}$ परत $y^{2}=4 a x$ में समानार्धी त्रिभुज की आवधारणिक पक्ष की आवश्यक लंबाई है।
उदाहरण 9 $(-3,1)$ से गुजरने वाला और $x$-axis को इसका मेजर धारा बनाने वालीकरण मान रखती हुई तिर्यक के मध्ये से गुजरने वाली अर्द्धनील की समीकरण ढूंढें।
समाधान आइए $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ को एक तिर्यक की समीकरण मानते हुए ($-3,1$) बिन्दु से गुजरने वाला तिर्यक हो सकता है।
इसलिए हमें है
$ \frac{9}{a^{2}}+\frac{1}{b^{2}}=1 $
या
$ 9 b^{2}+a^{2}=a^{2} b^{2} $
या
$ 9 a^{2}(a^{2}-e^{2})+a^{2}=a^{2} a^{2}(1-e^{2}) $
(यहाँ $b^{2}=a^{2}(1-e^{2})$
या
$ a^{2}=\frac{32}{3} $
फिर से
$ b^{2}=a^{2}(1-e^{2})=\frac{32}{3} \quad 1-\frac{2}{5}=\frac{32}{5} $
इसलिए, आवश्यक अर्धनील की समीकरण है
$ \begin{aligned} & \frac{x^{2}}{\frac{32}{3}}+\frac{y^{2}}{\frac{32}{5}}=1 \\ & 3 x^{2}+5 y^{2}=32 . \end{aligned} $
उदाहरण 10 $( \pm 6,0)$ एवं एक आवरणी ऋणात्मक $x=4$ हैं इसलिए हैताश्रेणी की समीकरण ढूंढें।
समाधान क्योंकि कोण यहां ($\pm a$, 0) परत के आतिशघटित हो रहे हैं और इनके मध्य बिन्दु मूल है, समीकरण का प्रकार $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ होता है।
यहां $b^{2}=a^{2}(e^{2}-1)$, कोण $( \pm a, 0)$ हैं और आवश्यक एकार्णिक $x= \pm \frac{a}{e}$ द्वारा दिये जा रहे हैं।
इसलिए $a=6, \frac{a}{e}=4$ और ऐसा $e=\frac{3}{2}$ जो $b^{2}=36 \frac{9}{4}-1=45$ देता है
इस प्रकार, आवश्यक हैताश्रेणी की समीकरण है $\frac{x^{2}}{36}-\frac{y^{2}}{45}=1$
उद्देश्य प्रकार सवाल
11 से 16 के प्रतिष्ठा उदाहरण के प्रत्येक के पास चार संभावित विकल्प होते हैं, जिनमें से एक सही होता है। दिए गए चार विकल्पों (MCQ) में से सही उत्तर चुनें।
उदाहरण 11 पहले तंत्र के प्रथम चतुर्थांश से संपर्क करने वाले उद्धरण की समीकरण है:
(A) $x^{2}+y^{2}-2 x-2 y+1=0$
(B) $x^{2}+y^{2}-2 x-2 y-1=0$
(C) $x^{2}+y^{2}-2 x-2 y=0$
(C) $x^{2}+y^{2}-2 x+2 y-1=0$
समाधान सही विकल्प (ए) है, क्योंकि समीकरण को $(x-1)^{2}+$ $(y-1)^{2}=1$ के रूप में लिखा जा सकता है जो एक वृत्त को दोनों धुरियों को छूने वाले हैं, परिधि $(1,1)$ और त्रिज्या एक इकाई।
~~Example 12 लाइन $3 x+y=14$ और $2 x+5 y=18$ के सन्निकट समांतराय के बीच के संदर्भबिन्दु से जो व्यास और बीज हैं, उनके माध्यम से केंद्र $(1,-2)$ वाले वृत्त का समीकरण होता है
परिभाषित करने के लिए $x^{2}+y^{2}-2 x+4 y-20=0$
(B) $x^{2}+y^{2}-2 x-4 y-20=0$
(C) $x^{2}+y^{2}+2 x-4 y-20=0$
(D) $x^{2}+y^{2}+2 x+4 y-20=0$
समाधान सही विकल्प (A) है। $3 x+y-14=0$ और $2 x$ $+5 y-18=0$ की सन्निवेशी बिंदु हैं $x=4, y=2$, अर्थात बिंदु $(4,2)$
इसलिए, त्रिज्या $=\sqrt{9+16}=5$ है और इसलिए वृत्त का समीकरण दिया जाता है
या
$ \begin{aligned} (x-1)^{2}+(y+2)^{2} & =25 \\ x^{2}+y^{2}-2 x+4 y-20 & =0 . \end{aligned} $
~~उदाहरण 13 पराबोला $x^{2}=12 y$ की मुख्य धुरिया के निवासियों से परस्पर सम्बन्धित बिन्दु को जो त्रिभुज बनाती है, उसका क्षेत्रफल है
(A) 12 वर्गीय इकाइयाँ
(B) 16 वर्गीय इकाइयाँ
(C) 18 वर्गीय इकाइयाँ
(D) 24 वर्गीय इकाइयाँ
समाधान सही विकल्प (C) है। चित्र से पता चलता है कि OPQ वह त्रिभुज है जिसका क्षेत्रफल निर्धारित करना है। त्रिभुज के क्षेत्रफल
$=\quad \frac{1}{2} PQ \times OF=\frac{1}{2}(12 \times 3)=18$
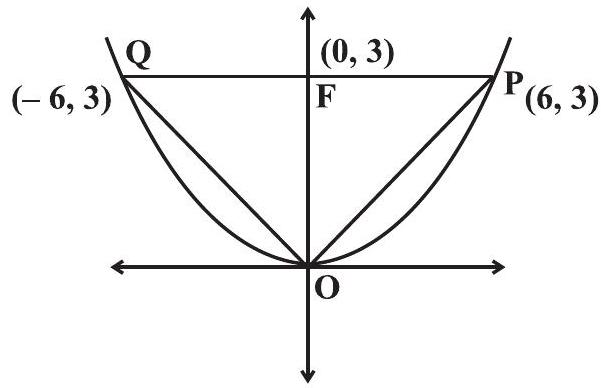
रेखाचित्र 11.11
~~उदाहरण 14 $y^{2}=6 x$ के दीर्घ फलनी के निवासियों के सन्निवेशी बिंदु से बिंदु $O$ तक जो रेखाएं होती हैं, उनकी समीकरण है
(A) $y \pm 2 x=0$
(B) $2 y \pm x=0$
(C) $x \pm 2 y=0$
(D) $2 x \pm y=0$
समाधान (B) सही विकल्प है। पराबोला $y^{2}=6 x$ और OP, OQ $O$ और बिंदु $P$ और $Q$ को जोड़ने वाली रेखाएँ होती हैं जिनकी आब्सिसा 24 हैं।
इसलिए
$ \begin{aligned} y^{2} & =6 \times 24=144 \\ y & = \pm 12 . \end{aligned} $
या
इसलिए बिंदु $P$ और $Q$ की निर्धारित संयोजक हैं $(24,12)$ और $(24,-12)$ हैं विकल्प सही हैं
$ y= \pm \frac{12}{24} x \quad 2 y \quad x . $
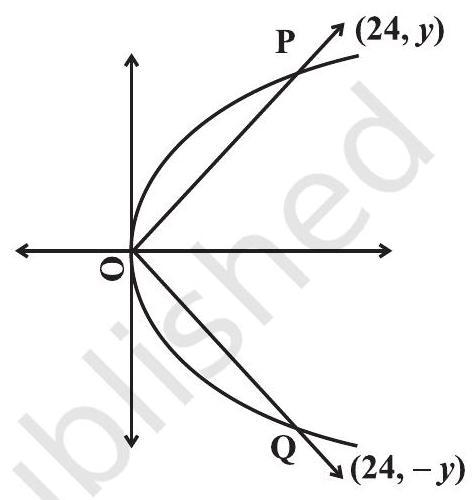
रेखाचित्र 11.12
~~उदाहरण 15 अक्षों के संकेंद्र में यह अंतर होता है और $x$-अक्ष में बड़ी धुरीया होती है, जो बिंदुओं $(-3,1)$ और $(2,-2)$ से गुजरती है
(A) $5 x^{2}+3 y^{2} 32$
(B) $3 x^{2}+5 y^{2}=32$
(C) $5 x^{2}-3 y^{2}=32$
(D) $3 x^{2}+5 y^{2}+32=0$
समाधान विकल्प (B) सही है। यदि $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ दृश्यु का समीकरण होती है। तो दिए गए शर्तों के अनुसार, हमें द्वारा लिया जाता है
$ \frac{9}{a^{2}}+\frac{1}{b^{2}}=1 \quad \text{ और } \quad \frac{1}{a^{2}}+\frac{1}{b^{2}}=\frac{1}{4} $
जो हमें देता है
$ a^{2}=\frac{32}{3} \quad \text{ और } \quad b^{2}=\frac{32}{5} . $
इसलिए, वृद्धि का समीकरण चाहिए $3 x^{2}+5 y^{2}=32$।
~~उदाहरण 16 एक हाइपरबोल की लंबवत धुरीया, जिसका केंद्र मूल में अनुक्रम 7 और वह $(5,-2)$ बिंदु से गुजरती है, हमें मिल जाता है, हाइपरबोल का समीकरण है
(A) $\frac{4}{49} x^{2}-\frac{196}{51} y^{2}=1$
(B) $\frac{49}{4} x^{2}-\frac{51}{196} y^{2}=1$
(C) $\frac{x^{2}}{25}-\frac{y^{2}}{16}=1$
Solution Let $x=a \sec \theta$ and $y=b \tan \theta$ represent the parametric equation of an ellipse with axis along $x$-axis and centre at origin. Then the latus rectum is $2 b^{2}=10$, so $b=\sqrt{5}$. Also, the distance between foci is $2 c=2 b=2 \sqrt{5}$. Let $2 a=2 \sqrt{{\sqrt{5}}^{2}+5}=2 \sqrt{10}$. Also,
$ \begin{aligned} & a^{2}=b^{2}+c^{2} \\ & \Rightarrow 10+5=10 \\ & \Rightarrow a=\sqrt{10} \end{aligned} $
Therefore, the equation of the ellipse is $\frac{x^{2}}{10}-\frac{y^{2}}{5}=1$ which is equivalent to $\frac{x^{2}}{25}-\frac{y^{2}}{16}=1$.
~~Example 22 The equation of the parabola with focus (2,0) and directrix $x=2$ is
Solution Since the given vertex is at the origin, the given focus is at $(2,0)$ and directrix is $x=2$, the parabola opens towards the right. The distance between the vertex and the focus is $2$ units.
Therefore, the equation of the parabola is $(x-2)^{2}=8 y$.
~~Example 23 If a circle passes through one of its own foci, its equation is
Solution Let $(r \cos \alpha,r \sin \alpha)$ be the coordinates of the given point.
Then by Pythagoras theorem,
$r^{2} \cos ^{2} \alpha+r^{2} \sin ^{2} \alpha=r^{2} \Rightarrow r=1$
So, the required equation of the circle is
$(x-\cos \alpha)^{2}+(y-\sin \alpha)^{2}=1$.
State whether the following statements are true or false. Justify.
~~Example 24 For any ellipse, semi-major axis is always greater than the semi-minor axis.
Solution True. In an ellipse, semi-major axis $(a)$ is always greater than the semi-minor axis $(b)$.
~~Example 25 An ellipse can only have two equal length perpendicular tangents.
Solution True. An ellipse can only have two equal length perpendicular tangents at the end points of its major axis.
समाधान दिया गया है कि $\frac{2 b^{2}}{a}=10$ और $2 a e=2 b \Rightarrow b=a e$
फिर से, हम जानते हैं कि
या
$ \begin{aligned} b^{2} & =a^{2}(1-e^{2}) \\ 2 a^{2} e^{2} & =a^{2} \Rightarrow e=\frac{1}{\sqrt{2}} \quad(\text{ इस्तेमाल करें } b=a e) \end{aligned} $
$ \text{ इस प्रकार } \quad a=b \sqrt{2} $
फिर से
$ \begin{aligned} \frac{2 b^{2}}{a} & =10 \\ b & =5 \sqrt{2} . \quad \text{ इस प्रकार हम प्राप्त करते हैं } a=10 \end{aligned} $
या
इसलिए, दिए गए उपवक्ता का समीकरण है
$ \frac{x^{2}}{100}+\frac{y^{2}}{50}=1 $
~~उदाहरण 22 यथार्थ $(2,3)$ बिन्दु ध्यान और रेखा $x-4 y+3=0$ है तथापि है जिसका समकोण है एक आपदा का समीकरण है
समाधान आपदा की परिभाषा का उपयोग करके, हमारे पास है
$ \sqrt{(x-2)^{2}+(y-3)^{2}}=|\frac{x-4 y+3}{\sqrt{17}}| $
स्क्वेयर करके, हम प्राप्त करते हैं
$ \begin{aligned} 17(x^{2}+y^{2}-4 x-6 y+13) & =x^{2}+16 y^{2}+9-8 x y-24 y+6 x \\ \text{ या } 16 x^{2}+y^{2}+8 x y-74 x-78 y+212 & =0 \end{aligned} $
~~उदाहरण 23 उपशीर्षक $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ की विस्तारिता $(3,0)$ और $(3 \sqrt{2}, 2)$ बिंदुओं से जोता है का विस्तारच्युटि है
समाधान दिया गया है कि उपशीर्षक $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ पार कर रही है $(3,0)$ और $(3 \sqrt{2}, 2)$ बिन्दुओं से हमें मिलता है $a^{2}=9$ और $b^{2}=4$।
फिर, हम जानते हैं कि $b^{2}=a^{2}(e^{2}-1)$। यह देता है
$ \begin{aligned} & 4=9(e^{2}-1) \\ & \text{ या } \\ & e^{2}=\frac{13}{9} \\ & \text{ या } \\ & e=\frac{\sqrt{13}}{3} \end{aligned} $
11.3 अभ्यास
लघु उत्तर विधि
~~
- एक परिधि के समकोण को छूने वाली व्यास $a$ होने की अवस्था में दोनों धराओं को छूने वाली संकेन्द्रित वन्दर बिन्दु की समीकरण खोजें।
~~ 2. दिखाएँ कि $(x, y)$ बिन्दु जिसे $x=\frac{2 a t}{1+t^{2}}$ और $y=\frac{a(1-t^{2})}{1+t^{2}}$ द्वारा दिया गया है सभी तर्कशो मान जिसके लिए $-1 \leq t \leq 1$ होता है एक परिधि पर स्थित होता है जहां $a$ कोई दिया गया वास्तविक संख्या है।
~~ 3. यदि एक परिधि कोई बिंदु पार करती है $(0,0)(a, 0),(0, b)$ तो इसके केंद्र की निर्धारित करें।
~~ 4. जो संधि के केंद्र होते हैं $(1,2)$ और जो $x$-अर्द्धमिथुन को छूनती है।
~~ 5. यदि रेखा $3 x-4 y+4=0$ और $6 x-8 y-7=0$ समांतर हैं तो एक परिधि की त्रिज्या ढूंढें।
[संकेत: दिये गए परावृत्तियों के द्वारा दिए गए समानांतर रेखाओं का दूरी, परिधि का व्यास को देती है।]
~~ 6. जो बिन्दु आवेश में स्थित होता है, वह दोनों धराओं को छूता है और तीसरी तार $3 x-4 y+8=0$ में पड़ती है और तीसरे वक्र पदार्थ में होता है।
[संकेत: $a$ संवेदी है, इसलिए $(-a,-a)$ केंद्र होगा और दिए गए रेखा से केंद्र की लम्बवत दूरी परिधि का व्यास देती है।]
~~ 7. यदि एक व्यास के द्वारा $(3,4)$, तो व्यास के दूसरे अंत का निर्धारण करें।
~~ 8. $(1,-2)$ के रूप में केंद्र होने और $3 x+y=14,2 x+5 y=18$ छूने वाले एक परिधि की समीकरण खोजें।
~~ 9. यदि रेखा $y=\sqrt{3} x+k$ को वृत्त $x^{2}+y^{2}=16$ पर छूती है, तो $k$ की मूल्य ढूंढें। [संकेत: केंद्र से इसके त्रिज्या तक लंबकता को इसके त्रिज्या को समान करें]।
~~
- वर्गमण्डल $x^{2}+y^{2}-6 x+12 y+15=0$ के समकक्ष और इसके क्षेत्रफल के दोगुना वाले वर्गमण्डल की समीकरण ढूंढें।
[संकेत: समकक्ष वर्गमण्डलों का समान केंद्र होता है।]
~~ 11. यदि संकुचित अक्ष की आधी लंबिता एक गोली तथा तीसरे हिस्से है, तो उसकी विसंगति ढूंढें।
~~ 12. समीकरण $9 x^{2}+25 y^{2}=225$ वाले संकुचित गोली और धाराओं की समीकरण।
~~ 13. यदि संकुचित गोली की विसंगति $\frac{5}{8}$ है और उसके भयों के बीच की दूरी 10 है, तो उसकी लंबिता ढूंढें।
~~ 14. वर्गमण्डल जिसकी विसंगति $\frac{2}{3}$ है, वह 5 है और उसका केंद्र $(0,0)$ है, उसकी समीकरण ढूंढें।
~~ 15. दोनों दिक्षेट्रिक के बीच की दूरी ढूंढें जो गोली का है $\frac{x^{2}}{36}+\frac{y^{2}}{20}=1$।
~~ 16. यदि पराबोला $y^{2}=8 x$ की फोकल दूरी 4 है, तो एक बिंदु की संख्या ढूंढें।
~~ 17. पराबोला $y^{2}=4 a x$ के शीर्ष बिंदु और पराबोला पर एक बिंदु के बीच की रेखांकन की लंबाई ढूंढें जहां रेखांकन $\theta$ के बीजी अक्ष के लिए किया जाता है।
~~ 18. यदि बिंदुओं $(0,4)$ और $(0,2)$ एक पराबोला के शीर्ष और फोकस हैं संपूर्ण लाभ की समीकरण ढूंढें।
~~ 19. यदि रेखा $y=m x+1$ एक पराबोला को स्पर्श करती है $y^{2}=4 x$ उसके लिए $m$ की मान्यता ढूंढें। [संकेत: रेखा और पराबोल की समीकरणों को समाधान करें, हम एक चद्यायी समीकरण प्राप्त करते हैं और फिर स्पर्श की स्थिति को लागू करते हैं जो $m$ की मान्यता देती है।]।
~~ 20. एक हाइपरबोला के भयों के बीच की दूरी 16 है और इसकी विसंगति $\sqrt{2}$ है, तो हाइपरबोला की समीकरण प्राप्त करें।
~~ 21. हाइपरबोला $9 y^{2}-4 x^{2}=36$ की विसंगति ढूंढें।
~~ 22. यदि गोली में विसंगति $\frac{3}{2}$ हो और भुवन $ (\pm 2,0)$ पर हों। हाइपरबोला की समीकरण प्राप्त करें।
लंबे उत्तर
~~ 23. यदि रेखाएँ $2 x-3 y=5$ और $3 x-4 y=7$ एक वर्गमण्डल के गोलों हैं और क्षेत्रफल 154 मरले इकाइयाँ हैं, तो वर्गमण्डल की समीकरण प्राप्त करें।
~~ 24. जिस वर्गमण्डल से गुजरती है जो बिंदु $(2,3)$ और $(4,5)$ से गुजरती है और केंद्र सीधी रेखा $y-4 x+3=0$ पर स्थित है, उसकी समीकरण प्राप्त करें।
~~ 25. वह गोला जिसका केंद्र $(3,-1)$ है और जो $2 x-5 y+18=0$ रेखा पर $6$ इकाइयों की धुरी काट रहा है, की समीकरण प्राप्त करें।
[संकेत: गोला के ऊतक की दूरी निर्धारित करने के लिए, दिए गए रेखा से केंद्र की लम्बवत दूरी ढूंढें।]
~~ 26. एक गोले की गोली से स्पर्श $x^{2}+y^{2}-2 x-4 y-20=0$ पर टच करने वाले एक गोले की समीकरण प्राप्त करें $(5,5)$।
~~ 27. प्रारंभिक दूरी $3$ इकाइयों के साथ वाली एक रेखांत में स्थित होने वाले एक गोले की समीकरण प्राप्त करें जो बिंदु $(7,3)$ से होती है और जिसका त्रिज्या $1$ इकाई होता है।
~~ 28. इन पराबोलों की समीकरण प्राप्त करें
(क) हाद रेखा $x=0$, फोकस बिंदु (6,0) रखें
(ब) शीर्ष बिंदु (0,4), फोकस बिंदु (0,2) रखें
(स) फोकस (-1,-2) पर, सतत रेखा $x-2 y+3=0$ रखें
~~ 29. वे सभी बिंदुओं की समीकरण प्राप्त करें जिनकी केंद्रीय बिंदुओं से दूरी की योग है $(3,0)$ और $(9,0)$ $12$।
~~ 30. वे सभी बिंदुओं की समीकरण प्राप्त करें जो $(0,4)$ से दूरी की दूसरी तिहाई हैं, उनकी दूरी $(0,9)$ से।
~~
-
साबित करें कि एक सभी बिन्दुओं का सेट ऐसा है जिसमें उनकी दूरियों का अंतर $(4,0)$ और $(-4,0)$ से हमेशा 2 के बराबर होता है, वह एक हाइपरबोला को प्रदर्शित करती है।
-
हाइपरबोला की समीकरण ढूंढेंः
(क) प्रायांगों $( \pm 5,0)$, संकेंद्रीया $( \pm 7,0)$ वाली हाइपरबोला है।
(ख) प्रायांगों $(0, \pm 7), e=\frac{4}{3}$ वाली हाइपरबोला है।
(ग) संकेंद्रीया $(0, \pm \sqrt{10})$ और $(2,3)$ से गुजरने वाली हाइपरबोला है।
उद्देश्य प्रकार के प्रश्न
यह बताएँ कि 33 से 40 तक के प्रश्नों के कथन सत्य हैं या असत्य हैं। उनका आधार दिखाएँ
~~ 33. रेखा $x+3 y=0$ एक वृत्त $x^{2}+y^{2}+6 x+2 y=0$ का व्यास है।
~~ 34. बिन्दु $(2,-7)$ से वृत्त $x^{2}+y^{2}-14 x-10 y-151=0$ की सबसे छोटी दूरी 5 के बराबर होती है।
[संकेंद्र और दिए गए बिंदु के बीच की दूरी और त्रिज्या का अंतर सबसे छोटी दूरी के बराबर होती है।]
~~ 35. यदि रेखा $l x+m y=1$ वृत्त $x^{2}+y^{2}=a^{2}$ का सप्रेकण है, तो बिंदु $(l, m)$ एक वृत्त पर स्थित होता है।
[संकेंद्र से दिए गए रेखा के मध्य बिंदु की दूरी, वृत्त का अर्धव्यास होती है।]
~~ 36. बिंदु $(1,2)$ वाली वृत्त $x^{2}+y^{2}-2 x+6 y+1=0$ के अंदर स्थित है।
~~ 37. रेखा $l x+m y+n=0$ पराबोला $y^{2}=4 a x$ को स्पर्श करेगी अगर $l n=a m^{2}$ हो।
~~ 38. यदि $P$ एक अंडकार्य $\frac{x^{2}}{16}+\frac{y^{2}}{25}=1$ पर एक संकेंद्र है जिसके संकेंद्रों की दूरियों का योग $S$ और $S^{\prime}$ है, तो $PS+PS^{\prime}=8$ होगा।
~~ 39. रेखा $2 x+3 y=12$ उद्रेक $\frac{x^{2}}{9}+\frac{y^{2}}{4}=2$ को बिंदु $(3,2)$ पर स्पर्श करती है।
~~ 40. रेखाओं $\sqrt{3} x-y-4 \sqrt{3} k=0$ और $\sqrt{3} k x+k y-4 \sqrt{3}=0$ के छोटू के बीच परिच्छेद पर बिंदु का संकीर्ण $k$ का लोकस हाइपरबोला है जिसकी उत्कृष्टता 2 है।
[सूत्र $k$ को दिए गए समीकरणों के बीच समाप्त करें]
खाली जगह भरें 41 से 46 के अभ्यास में।
~~ 41. दीर्घाओं वाले वृत्त की समीकरण ढूंढेः $(3,-4)$ केंद्र वाले वृत्त जो $5 x+12 y-12=0$ से स्पर्श करता है
[केंद्र से वृत्त की लंबवत दूरी को ढूंढने के लिए धीर्यामिति रेखा के बीच की लंबवत दूरी खोजें।]
~~ 42. चतुर्भुज की संरेखाओं $y=x+2,3 y=4 x, 2 y=3 x$ से घिरी कोणाकृति की समीकरण ढूंढेः
~~ 43. एक अविनाशी तार का उपयोग करके एक अंडाकार्य वृत्त को चिह्नित किया जाता है। यदि ब्यास $6 cm$ और छोटी धुरी $4 cm$ है, तो तार की लंबाई और दोनों धुरियों के बीच की दूरी स्थान में से होगी
~~ 44. तारों से लंबित वृत्त की समीकरण ढूंढेः $(0,1),(0,-1)$ संकेन्द्र और 1 की छोटी धुरी वाले अंडाकारी वृत्त की समीकरण है
~~ 45. तारों से लंबित गुहारेखा की समीकरण ढूंढेः $(-1,-2)$ स्थितीकरण और $x-2 y+3=0$ सीधी रेखा वाले पराबोला की समीकरण है
~~ 46. प्रायांगों $(0, \pm 6)$ और उत्कार्शता $\frac{5}{3}$ वाली हाइपरबोला की समीकरण और संकेन्द्रों की स्थानांतर हैं
- संकेतक $y$-अक्ष पर केंद्र और मूलबिंदु और बिंदु $(2,3)$ से गुजरने वाले वृत्त का समीकरण होगा
(A) $x^{2}+y^{2}+13 y=0$
(B) $3 x^{2}+3 y^{2}+13 x+3=0$
(C) $6 x^{2}+6 y^{2}-13 x=0$
(D) $x^{2}+y^{2}+13 x+3=0$
~~ 50. जिसका मूलबिंदु मूलबिंदु मान और जो एक समबाहु त्रिभुज के शीर्षक बिंदु से जाती है, उसका समीकरण होगा
(A) $x^{2}+y^{2}=9 a^{2}$
(B) $x^{2}+y^{2}=16 a^{2}$
(C) $x^{2}+y^{2}=4 a^{2}$
(D) $x^{2}+y^{2}=a^{2}$
[संकेत: त्रिभुज का केंद्रियवृत्त केंद्र केंद्र के साथ मेल खाता है और वृत्त की त्रिज्या माध्यांक की लंबाई का $\frac{2}{3}$ है]
~~ 51. यदि एक पराबोला का फोकस $(0,-3)$ है और उसका निर्देशक रेखा $y=3$ है, तो इसका समीकरण होगा
(A) $x^{2}=-12 y$
(B) $x^{2}=12 y$
(C) $y^{2}=-12 x$
(D) $y^{2}=12 x$
~~ 52. यदि पराबोला $y^{2}=4 a x$ बिंदु $(3,2)$ से गुजरती है, तो इसकी मापदंड ऊँचाई होगी
(A) $\frac{2}{3}$
(B) $\frac{4}{3}$
(C) $\frac{1}{3}$
(D) 4
~~ 53. पराबोला का ध्रुव बिन्दु $(-3,0)$ होता है और निर्देशक रेखा रेखा $x+5=0$ होती है, तो इसका समीकरण होगा
(A) $y^{2}=8(x+3)$
(B) $x^{2}=8(y+3)$
(C) $y^{2}=-8(x+3)$
(D) $y^{2}=8(x+5)$
~~ 54. वृत्ताकार जिसका केंद्र वृत्ताकार $(1,-1)$, निर्देशक रेखा यह रेखा $x-y-3=0$ है और उत्कृष्टता $\frac{1}{2}$ होती है
(A) $7 x^{2}+2 x y+7 y^{2}-10 x+10 y+7=0$
(B) $7 x^{2}+2 x y+7 y^{2}+7=0$
(C) $7 x^{2}+2 x y+7 y^{2}+10 x-10 y-7=0$
(D) कोई नहीं
~~ 55. वृत्ताकार $3 x^{2}+y^{2}=12$ का फलाक की लंबाई होगी
(A) 4
(B) 3
(C) 8
(D) $\frac{4}{\sqrt{3}}$
~~ 56. यदि $e$ वृत्ताकार $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a<b)$ की अत्यधिकता है, तो
(A) $b^{2}=a^{2}(1-e^{2})$
(B) $a^{2}=b^{2}(1-e^{2})$
(C) $a^{2}=b^{2}(e^{2}-1)$
(D) $b^{2}=a^{2}(e^{2}-1)$
~~ 57. जिसकी बन्दरगाह 8 और पारसंचरी अक्ष फोकसों के बीच की दूरी के आधा होता है वह ह्यूपरबोल की अत्यधिकता होती है
(A) $\frac{4}{3}$
(B) $\frac{4}{\sqrt{3}}$
(C) $\frac{2}{\sqrt{3}}$
(D) इनमें से कोई नहीं
~~ 58. जर्दोज़ी के बीच की दूरी 16 है और इसकी अत्यधिकता $\sqrt{2}$ है, इसका समीकरण होगा
(A) $x^{2}-y^{2}=32$
(B) $\frac{x^{2}}{4}-\frac{y^{2}}{9}=1$
(C) $2 x-3 y^{2}=7$
(D) इनमें से कोई नहीं
~~ 59. फोकस $ (\pm 2,0)$ पर आने वाली और अत्यधिकता $\frac{3}{2}$ होने वाले ह्यूपरबोल का समीकरण होगा
(A) $\frac{x^{2}}{4}-\frac{y^{2}}{5}=\frac{4}{9}$
(B) $\frac{x^{2}}{9}-\frac{y^{2}}{9}=\frac{4}{9}$
(C) $\frac{x^{2}}{4}-\frac{y^{2}}{9}=1$
(D) इनमें से कोई नहीं







