आंकड़े
अध्याय 15
सांख्यिकी
15.1 अवलोकन
पहले कक्षाओं में, आपने अवरुद्ध और ऐक्य के मापों का अध्ययन किया है, जैसे कि गणना और माध्य डाटा का माध्य और मध्यांक. इन मापों के अलावा, हमें अक्सर एक दूसरे प्रकार के माप को भी गणना करने की जरूरत होती है जिसे औसत या मध्यांक आदि के बारे में आंकलन कहा जाता है.
इस अध्याय में कुछ महत्वपूर्ण विस्तार के माप जैसे कि औसत असंख्यता, विचलन, मानक विचलन आदि के साथ संबंधित हैं, और अंत में आकृति वितरण का विश्लेषण।
15.1.1 विस्तार के माप
(a) दस्तीयता न्यायसंगत माप
विस्तार का माप जो सबसे सरलतम तरीके से समझ में आता है और सबसे आसानी से गणना किया जा सकता है वह है। विस्तार की परिभाषा है:
विस्तार = सबसे बड़ा अवलोकन - सबसे छोटा अवलोकन
(b) औसत असंख्यता
(i) असंख्यता के लिए औसत असंख्यता:
$n$ अवलोकन $x_1, x_2, \ldots, x_n$ के लिए, उनकी औसत $\bar{{}x}$ के बारे में औसत असंख्यता निम्नलिखित है
$ \operatorname{एमडी}(\bar{{}x})=\frac{|x_i-\bar{{}x}|}{n} $
उनके मध्यांक $म्$ के बारे में असंख्याता होती है
$ \begin{aligned} \frac{|x_i-M|}{n} \text{2} \end{aligned} $
(ii) विछिन्न मात्रायुक्त वितरण के लिए औसत असंख्यता
दिए गए आंकड़े $x_1, x_2, \ldots, x_n$ मिलेंगे जो अवधारित अवलोकन $f_1, f_2, \ldots, f_n$ के साथ पाए जाते हैं। इस स्थिति में
$ \begin{aligned} & \operatorname{एमडी}(\bar{{}x})=\frac{f_i|x_i-\bar{{}x}|}{f_i}=\frac{f_i|x_i-\bar{{}x}|}{N} \text{3}\\ & \operatorname{एमडी}(म्)=\frac{f_i|x_i-M|}{N} \text{4} \end{aligned} $
यहां $N=f_i$ है।
(iii) निरंतर आवृत्ति वितरण के लिए औसत असंख्यता (समूही डाटा).
$ \begin{aligned} & \operatorname{एमडी}(\bar{{}x})=\frac{f_i|x_i-\bar{{}x}|}{N} \text{5}\\ & \operatorname{एमडी}(म्)=\frac{f_i|x_i-M|}{N} \text{6} \end{aligned} $
यहां $x_i$ वर्गों के माध्यांक हैं, $\bar{{}x}$ और $M$ प्रत्येक संचालन की औसत और माध्यांक हैं।
(c) विचलन: लेट् $x_1, x_2, \ldots, x_n$ हों $n$ अवलोकन में माध्य होने के साथ $\bar{{}x}$। विचलन, $\sigma^{2}$ द्वारा चिह्नित होता है, निम्नलिखित है
$ \begin{aligned} \sigma^{2}=\frac{1}{n}(x_i-\bar{{}x})^{2} \text{7} \end{aligned} $
(d) मानक विचलन: यदि $\sigma^{2}$ विचलन है, तो $\sigma$, मानक विचलन कहलाता है, निम्नलिखित है
$ \begin{aligned} \sigma=\sqrt{\frac{1}{n}(x_i-\bar{{}x})^{2}} \text{8} \end{aligned} $
(e) एक विकर्ण मात्रायुक्त वितरण के लिए मानक विचलन निम्नलिखित है
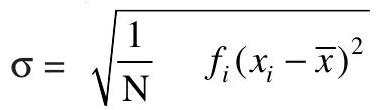
यहां $f_i^{\prime}$ s $x_i{ }^{\prime} s$ की आवृत्तियाँ हैं और $N= _{i=1}^{n} f_i$।
(f) निरंतर आवृत्ति वितरण (समूही डाटा) के लिए मानक विचलन निम्नलिखित है
$ \begin{aligned} \sigma=\sqrt{\frac{1}{N} \quad f_i(x_i-\bar{{}x})^{2}} \text{10} \end{aligned} $
यहां $x_i$ कक्षाओं के मध्यबिन्दु हैं और $f_i$ उनकी संबंधित संख्याओं हैं।
सूत्र (10) उसी समान है
वेरधिति \sigma = \frac{{1}}{{N}} \sqrt{{N \quad f_i x_i^{2}-(f_i x_i)^{2}}} \text{11} \end{aligned} $
(g) और भी एक साधारण बीजी के लिए सूचकांक:
$ \begin{aligned} \sigma_x=\frac{{h}}{{N}} \sqrt{{N \quad f_i y_i^{2}-(f_i y_i)^{2}}} \text{12} \end{aligned} $
यहाँ $h$ क्रमवों की चौड़ाई है और $y_i=\frac{{x_i-A}}{{h}}$ है और $A$ मान्य मान है।
15.1.2 प्रतिष्ठापना वार्यवलन का संकेतक कभी-कभी सूचित करने के लिए उपयोगी होता है जिसमें चौड़ाई गयी मानक विचरण को माध्यिका के रूप में व्यक्त किया जाता है, आम तौर पर प्रतिशत में। इसके लिए यह कार्यप्रतिक्रिया देखें
$ \text{ आपुर्ति गठन }=\frac{{\text{ विचरण }} {\text{ साधारणता }}}{100} $
15.2 हल किए हुए मामले
##छोटे उत्तर प्रकार
~~उदाहरण 1 निम्नलिखित डेटा की औसत विचरण साधारिता का ज्ञात कीजिए:
| आकार $(\boldsymbol{{}x}):$ | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
|---|---|---|---|---|---|---|---|---|
| आवृत्ति $(\boldsymbol{{}f}):$ | 3 | 3 | 4 | 14 | 7 | 4 | 3 | 4 |
तथ्यात्मक चालचित्र $=\bar{{}x}=\frac{{f_i x_i}}{{f_i}}=\frac{{3+9+20+98+63+44+39+60}}{{42}}=\frac{{336}}{{42}}=8$
M.D. $(\bar{{}x})=\frac{{f_i|x_i-\bar{{}x}}|}={{f_i}}=\frac{{3(7)+3(5)+4(3)+14(1)+7(1)+4(3)+3(5)+4(7)}}{{42}}$ $=\frac{{21+15+12+14+7+12+15+28}}{{42}}=\frac{{62}}{{21}}=2.95$
~~उदाहरण 2 निम्नलिखित डेटा के लिए विचलन और मानक विचरण की गणना कीजिए:
$57,64,43,67,49,59,44,47,61,59$
तथ्यात्मक चालचित्र $(\bar{{}x})=\frac{{57+64+43+67+49+59+61+59+44+47}}{{10}}=\frac{{550}}{{10}}=55$
$ \begin{aligned} & \text{ विचरण }(\sigma^{2})=\frac{{(x_i-\bar{{}x})^{2}}}{{n}} \\ & =\frac{{2^{2}+9^{2}+12^{2}+12^{2}+6^{2}+4^{2}+6^{2}+4^{2}+11^{2}+8^{2}}}{{10}} \\ & = \\ & \frac{{662}}{{10}}=66.2 \end{aligned} $
मानक विचरण $(\sigma)=\sqrt{{\sigma^{2}}}=\sqrt{{66.2}}=8.13$
~~उदाहरण 3 साधारित डेटा के मानक विचरण के लिए दो सूत्र दिखाएं।
$ \sigma=\sqrt{{\frac{{(x_i-\bar{{}x})^{2}}}{{n}}}} \quad \text{ और } \sigma^{\prime}=\sqrt{{\frac{{x_i^{2}}}{{n}}-\bar{{}x}^{2}}} $
सामग्रीतथ्यात्मक हैं यह की, $(x_i-\bar{{}x})^{2}=(x_i^{2}-2 \bar{{}x} x_i+\bar{{}x}^{2})$
$ \begin{aligned} & \quad=x_i^{2}+-2 \bar{{}x} x_i+\bar{{}x}^{2} \\ & =x_i^{2}-2 \bar{{}x} \quad x_i+(\bar{{}x})^{2} \quad 1 \\ & =\quad x_i^{2}-2 \bar{{}x}(n \bar{{}x})+n \bar{{}x}^{2} \\ & =x_i^{2}-n \bar{{}x}^{2} \end{aligned} $
दोनों पक्षों को $n$ से भांगरभूत करके और उनकी वर्गमूल लेते हैं, हमें $\sigma=\sigma^{\prime}$ मिलता है।
~~उदाहरण 4 निम्नलिखित डेटा का विचरण गणना कीजिये :
| वर्ग अवधि | आवृत्ति |
|---|---|
| $4-8$ | 3 |
| $8-12$ | 6 |
| $12-16$ | 4 |
| $16-20$ | 7 |
$औसत(\bar{{}x})=\frac{{f_i x_i}}{{f_i}}=\frac{{3 \times 6+6 \times 10+4 \times 14+7 \times 18}}{{20}}=13$
तथ्यात्मक विचरण $(\sigma^{2})=\frac{{f_i(x_i-\bar{{}x})^{2}}}{{f_i}}=\frac{{3(-7)^{2}+6(-3)^{2}+4(1)^{2}+7(5)^{2}}}{{20}}$
$ =\frac{{147+54+4+175}}{{20}}=19 $
लंबा जवाब प्रकार
~~उदाहरण 5 निम्नलिखित आवृत्ति वितरण की माध्यिका, हल्कापन और मानक विचरण की गणना कीजिये:
| समूह | आवृत्ति |
|---|---|
| $1-10$ | 11 |
| $10-20$ | 29 |
इसका हिंदी संस्करण क्या है: | $20-30$ | 18 | | $30-40$ | 4 | | $40-50$ | 5 | | $50-60$ | 3 |
समाधान ए दिया गया मान $A$ हो, जो कि 25.5 होता है। यहाँ $h=10$
| वर्ग | $\boldsymbol{{}x} _{\boldsymbol{{}i}}$ | $\boldsymbol{{}y} _{\boldsymbol{{}i}}=\frac{\boldsymbol{{}x} _{\boldsymbol{{}i}}-\mathbf{2 5 . 5}}{\mathbf{1 0}}$ | $\boldsymbol{{}f} _{\boldsymbol{{}i}}$ | $\boldsymbol{{}f} _{\boldsymbol{{}i}} \boldsymbol{{}y} _{\boldsymbol{{}i}}$ | $\boldsymbol{{}f} _{\boldsymbol{{}i}} \boldsymbol{{}y} _{\boldsymbol{{}i}}^{\mathbf{2}}$ |
|---|---|---|---|---|---|
| $1-10$ | 5.5 | -2 | 11 | -22 | 44 |
| $10-20$ | 15.5 | -1 | 29 | -29 | 29 |
| $20-30$ | 25.5 | 0 | 18 | 0 | 0 |
| $30-40$ | 35.5 | 1 | 4 | 4 | 4 |
| $40-50$ | 45.5 | 2 | 5 | 10 | 20 |
| $50-60$ | 55.5 | 3 | 3 | 9 | 27 |
$ x^{\prime}=\frac{f_i y_i}{f_i}=\frac{-28}{70}=-0.4 $
माध्य रूपी $=\bar{{}x}=25.5+(-10)(0.4)=21.5$
व्यारियंस
$ \begin{aligned} & (\sigma^{2})=\frac{h}{N}{\sqrt{N} f_i y_i^{2}-(f_i y_i)^{2}}^{2} \\ & =\frac{10 \times 10}{70 \times 70}[70(124)-(-28)^{2}] \\ & =\frac{70(124)}{7 \times 7}-\frac{28 \times 28}{7 \times 7}=\frac{1240}{7}-16=161 \\ & \text{ S.D. }(\sigma)=\sqrt{161}=12.7 \end{aligned} $
~~उदाहरण 6 दो कारखानों ए और बी द्वारा उत्पन्न बल्बों का जीवन निम्नानुसार है:
| जीवन अवधि (घंटे में) |
कारख़ाना ए (बल्बों की संख्या) |
कारख़ाना बी (बल्बों की संख्या) |
|---|---|---|
| $550-650$ | 10 | 8 |
| $650-750$ | 22 | 60 |
| $750-850$ | 52 | 24 |
| $850-950$ | 20 | 16 |
| $950-1050$ | 16 | 12 |
जीवन आयाम के दृष्टिकोण से किस कारख़ाने के बल्बों में अधिक संगति होती है?
समाधान यहाँ $h=100$, एस (संकेतित माध्य) $=800$ है।
| जीवन अवधि (घंटे में) |
बीची मान $(x_i)$ | $=\frac{x_i-\mathbf{A}}{10}$ | कारख़ाना ए | कारख़ाना बी | ||||
|---|---|---|---|---|---|---|---|---|
| कारख़ाना ए | $f_i y_i$ | $f_i y_i^{2}$ | कारख़ाना बी | $f_i y_i$ | $f_i y_i^{2}$ | |||
| $550-650$ | 600 | 10 | -20 | 40 | 8 | -16 | 32 | |
| $650-750$ | 700 | 22 | -22 | 22 | 60 | -60 | 60 | |
| $750-850$ | 800 | 0 | 52 | 0 | 0 | 24 | 0 | 0 |
| $850-950$ | 900 | 1 | 20 | 20 | 20 | 16 | 16 | 16 |
| $950-1050$ | 1000 | 2 | 16 | 32 | 64 | 12 | 24 | 48 |
| 120 | 10 | 146 | 120 | -36 | 156 |
कारख़ाना ए के लिए
$ \begin{aligned} \text{ मान }(\bar{{}x}) & =800+\frac{10}{120} \times 100=816.67 \text{ घंटे } \\ \text{ S.D. } & =\frac{100}{120} \sqrt{120(146)-100}=109.98 \end{aligned} $
इसलिए, प्रतिशत चर विवरण $(C.V.)=\frac{\text{ S.D. }}{\bar{{}x}} \times 100=\frac{109.98}{816.67} \times 100=13.47$
कारख़ाना बी के लिए
$ \begin{aligned} \text{ मान } & =800+\frac{-36}{120} \quad 100=770 \\ \text{ S.D. } & =\frac{100}{120} \sqrt{120(156)-(-36)^{2}}=110 \end{aligned} $
इसलिए, प्रतिशत चर विवरण $(C.V.)=\frac{\text{ S.D. }}{\text{ मान }} \times 100=\frac{110}{770} \times 100=14.29$
कंटेंट का हे लेकिन ही संस्करण क्या है: यदि फ़ैक्ट्री बी का C.V. $>$ फ़ैक्ट्री का C.V. $A \Rightarrow$ फ़ैक्ट्री $B$ में अधिकता है जो इसका मतलब है कि फ़ैक्ट्री $A$ के बल्ब अधिक सतत हैं।
प्रयोग प्रकार के प्रश्न
म.0.के हर उदाहरण के चार विकल्पों में से सही उत्तर चुनें (एम.सी.क्यू.)
~~उदाहरण 7 औसत गणितीय विचलन $2, 9, 9, 3, 6, 9, 4$ के दूसरे से अंतरित रूप से
(A) 2.23
(B) 2.57
(C) 3.23
(D) 3.57
समाधान (B) सही उत्तर है
$ \text{ औसत गणितीय विचलन }(\bar{{}x})=\frac{|x_i-\bar{{}x}|}{n}=\frac{4+3+3+3+0+3+2}{7}=2.57 $
~~उदाहरण 8 आंकड़े $2, 4, 5, 6, 8, 17$ का संक्रमित कोई विचलन $23.33$ है। तो $4, 8, 10, 12, 16, 34$ का संक्रमित कोई विचलन होगा
(A) 23.23
(B) 25.33
(C) 46.66
(D) 48.66
समाधान (C) सही उत्तर है. हर आंकड़े को 2 से गुणित करने पर विचलन भी दोगुना होता है।
~~उदाहरण 9 एक सेट $n$ मान वाले $x_1, x_2, \ldots, x_n$ के मानक विचलन $6$ है। $n$ मान वाले $x_1+k, x_2+k, \ldots, x_n+k$ का मानक विचलन होगा
(A) $\sigma$
(B) $\sigma+k$
(C) $\sigma-k$
(D) $k \sigma$
समाधान (A) सही उत्तर है। यदि प्रत्येक आंकड़ा एक स्थिर $k$ से बढ़ाया जाता है, तो मानक विचलन बरकरार रहता है।
15.3 अभ्यास
संक्षेप उत्तर प्रकार
~~
- वितरण के औसत के बारे में औसत गणितीय विचलन ढूंढें:
| आकार | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|
| आवृत्ति | 6 | 4 | 5 | 1 | 4 |
~~ 2. निम्नलिखित वितरण के मध्य सामान्य गणितीय विचलन ढूंढें:
| प्राप्त अंक | 10 | 11 | 12 | 14 | 15 |
|---|---|---|---|---|---|
| छात्रों की संख्या | 2 | 3 | 8 | 3 | 4 |
~~ 3. जब $n$ विषम संख्या होती है तो पहली $n$ के प्राकृतिक संख्याओं के साधारण गणितीय विचलन का औसत गणितीय विचलन कीजिए।
~~ 4. जब $n$ जो भी हो विषम संख्या होती है, तो पहले $n$ प्राकृतिक संख्याओं के साधारण गणितीय विचलन का औसत गणितीय विचलन कीजिए।
~~ 5. पहले $n$ प्राकृतिक संख्याओं का मानक विचलन ढूंढें।
~~ 6. एक परीक्षा पूरी करने के लिए समय के लिए कुछ आंकड़े का औसत और मानक विचलन निम्न परिणामों के साथ गणना की गई है:
अवलोकनों की संख्या $=25$, औसत $=18.2$ सेकंड, मानक विचलन $=3.25$ सेकंड।
इसके अलावा, एक और सेट अवलोकन $x_1, x_2, \ldots, x _{15}$, भी सेकंड में उपलब्ध हैं, और हमारे पास $x _{i=1}^{15}=279$ और $x_i^{2}=5524$ है। सभी 40 अवलोकनों पर आधारित मानक विचलन की गणना करें।
~~ 7. $n_1$ अवलोकनों का औसत और मानक विचलन $\bar{{}x}_1$ और $s_1$ है, जबकि $n_2$ अवलोकनों का औसत और मानक विचलन $\bar{{}x}_2$ और $s_2$ होता है। दिखाएं कि $(n_1+n_2)$ अवलोकनों का मानक विचलन निम्नलिखित से दिया जाता है
एसडी $=\sqrt{\frac{n_1(s_1)^{2}+n_2(s_2)^{2}}{n_1+n_2}+\frac{n_1 n_2(\bar{{}x}_1-\bar{{}x}_2)^{2}}{(n_1+n_2)^{2}}}$
~~
- दो सेटों में प्रत्येक 20 अवलोकन हैं, जिनकी सामान्य विचलन 5 है। पहले सेट का औसत 17 है और दूसरे सेट का औसत 22 है। दिए गए दो सेटों को मिलाकर प्राप्त सेट का मानक विचलन निर्धारित करें।
~~ 9. आवृत्ति वितरण:
| $\boldsymbol{{}x}$ | $A$ | $2 A$ | $3 A$ | $4 A$ | $5 A$ | $6 A$ |
|---|---|---|---|---|---|---|
| $\boldsymbol{{}f}$ | 2 | 1 | 1 | 1 | 1 | 1 |
यहां $A$ एक सकारात्मक पूर्णांक है, जिसका विचलन 160 है। $A$ की मान का निर्धारण करें।
~~ 10. आवृत्ति वितरण के लिए:
| $\boldsymbol{{}x}$ | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| $\boldsymbol{{}f}$ | 4 | 9 | 16 | 14 | 11 | 6 |
मानक वितरण ढूंढें।
~~ 11. एक कक्षा में 60 छात्र हैं। निम्नलिखित छात्रों द्वारा प्राप्त अंकों का आवृत्ति वितरण यहां है:
| अंक | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| आवृत्ति | $x-2$ | $x$ | $x^{2}$ | $(x+1)^{2}$ | $2 x$ | $x+1$ |
यहां $x$ एक सकारात्मक पूर्णांक है। अंकों का माध्य और मानक विचलन निर्धारित करें।
~~ 12. 60 बल्बों के एक नमूने का औसत जीवन 650 घंटे था और मानक विचलन 8 घंटे था। दूसरे नमूने में 80 बल्बों का औसत जीवन 660 घंटे होता है और मानक विचलन 7 घंटे होता है। समग्र मानक विचलन ढूंढें।
~~ 13. 100 वस्तुओं का औसत और मानक विचलन 50 और 4 होता है, क्रमशः। सभी वस्तुओं का योग और वस्तुओं के वर्गों का योग ढूंढें।
~~ 14. यदि एक वितरण के लिए $(x-5)=3$, $(x-5)^{2}=43$ है और कुल वस्तुओं की संख्या 18 है, तो माध्य और मानक विचलन ढूंढें।
~~ 15. निम्नलिखित आवृत्ति वितरण का माध्य और वेरियेंस ढूंढें:
| $\boldsymbol{{}x}$ | $1 \leq x<3$ | $3 \leq x<5$ | $5 \leq x<7$ | $7 \leq x<10$ | |
|---|---|---|---|---|---|
| $\boldsymbol{{}f}$ | 6 | 4 | 5 | 1 |
लंबे जवाब का प्रकार
~~ 16. निम्नलिखित आवृत्ति वितरण के लिए माध्य से माध्यम भिन्नता निर्धारित करें:
| वर्ग अवधि | $0-4$ | $4-8$ | $8-12$ | $12-16$ | $16-20$ |
|---|---|---|---|---|---|
| आवृत्ति | 4 | 6 | 8 | 5 | 2 |
~~ 17. निम्नलिखित आंकड़ों के माध्य से माध्य भिन्नता की गणना करें:
| वर्ग अवधि | $0-6$ | $6-12$ | $12-18$ | $18-24$ | $24-30$ |
|---|---|---|---|---|---|
| आवृत्ति | 4 | 5 | 3 | 6 | 2 |
~~ 18. निम्नलिखित वितरण के लिए माध्य और मानक विचलन निर्धारित करें:
| अंक | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| आवृत्ति | 1 | 6 | 6 | 8 | 8 | 2 | 2 | 3 | 0 | 2 | 1 | 0 | 0 | 0 | 1 |
~~ 19. 70 जारों में कॉफी के वजन को निम्नलिखित सारणी में दिखाया गया है:
| वजन (ग्राम) |
आवृत्ति |
|---|---|
| $200-201$ | 13 |
| $201-202$ | 27 |
| $202-203$ | 18 |
| $203-204$ | 10 |
| $204-205$ | 1 |
| $205-206$ | 1 |
प्रदान वितरण का विचलन और मानक विचलन निर्धारित करें।
~~ 20. पहली $n$ टर्म के और्थमेटिक प्रोग्रेशन के औसत और मानक विचलन की तलाश करें जिसका पहला टर्म $a$ है और समान अंतर है $d$।
~~ 21. निम्नलिखित हैं दो छात्रों रवि और हशिना द्वारा 10 परीक्षाओं में प्राप्त अंक, प्रति 100।
| रवि | 25 | 50 | 45 | 30 | 70 | 42 | 36 | 48 | 35 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|
| हशिना | 10 | 70 | 50 | 20 | 95 | 55 | 42 | 60 | 48 | 80 |
कौन ज्यादा बुद्धिमान है और कौन स्थिर?
~~ 22. 100 अवलोकनों का औसत और मानक विचलन मिला था जिनकी मान्यता 40 और 10 थी। यदि गणना के समय दो अवलोकनों को गलती से 30 और 70 के बदले में 3 और 27 लिया गया था, तो सही मानक विचलन का पता लगाएं।
~~ 23. 10 पठनों के औसत और विचलन की गणना करते समय, एक छात्र ने गलती से सही पठन 25 के लिए पठन 52 का उपयोग किया। उसने औसत और विचलन को 45 और 16 के रूप में प्राप्त किया। सही औसत और विचलन का पता लगाएं।
उद्देश्य प्रकार के प्रश्न
निम्नलिखित में से प्रत्येक अभ्यास 24 से 39 (एम।सी।क्यू।) में दिए गए चार विकल्पों में से सही उत्तर चुनें।
~~ 24. डेटा $3,10,10,4,7,10,5$ का माध्य डेविएशन
(A) 2
(B) 2.57
(C) 3
(D) 3.75
~~ 25. $n$ उत्पन्न $x_1, x_2, \ldots, x_n$ के औसत से माध्य डेविएशन इस प्रकार दिया जाता है
(A) $ _{i=1}^{n}(x_i-\bar{{}x})$
(B) $\frac{1}{n} _{i=1}^{n}|x_i-\bar{{}x}|$
(C) $ _{i=1}^{n}(x_i-\bar{{}x})^{2}$
(D) $\frac{1}n _{i=1}^{n}(x_i-\bar{{}x})^{2}$
~~ 26. जब परीक्षण किया गया, उनकी जीवन (घंटों में) के 5 बल्बों की योग्यता निम्न है: $1357,1090,1666,1494,1623$
इससे उनके माध्य से डेविएशन योग्यता (घंटों में) है
(A) 178
(B) 179
(C) 220
(D) 356
~~ 27. इस प्रकार सारणी में 9 छात्रों द्वारा गणित परीक्षा में प्राप्त अंक हैं: $50,69,20,33,53,39,40,65,59$
माध्य से माध्य डेविएशन है:
(A) 9
(B) 10.5
(C) 12.67
(D) 14.76
~~ 28. डेटा $6,5,9,13,12,8,10$ का मानक विचलन है
(A) $\sqrt{\frac{52}{7}}$
(B) $\frac{52}{7}$
(C) $\sqrt{6}$
(D) 6
~~ 29. $x_1, x_2, \ldots, x_n$ न हों, औसत $\bar{{}x}$ हो, तब मानक विचलन के लिए सूत्र दिया जाता है
(A) $\quad(x_i-\bar{{}x})^{2}$
(B) $\frac{(x_i-\bar{{}x})^{2}}{n}$
(C) $\sqrt{\frac{(x_i-\bar{{}x})^{2}}{n}}$
(D) $\sqrt{\frac{x_i^{2}}{n}+\bar{{}x}^{2}}$
~~ 30. 100 अवलोकनों का औसत 50 है और उनका मानक विचलन 5 है। सभी अवलोकनों के वर्गों का योग है
(A) 50000
(B) 250000
(C) 252500
(D) 255000
~~ 31. आ, बी, सी, डी, ई अवलोकन अवधारणा के साथ हैं और उनका औसत $म$ और मानक विचलन $एस$ है। अवलोकन $क+ए, ब+क, स+क, ड+क, ई+क$ का मानक विचलन है
(A) $एस$
(B) $क एस$
(C) $एस+क$
(D) $\frac{एस}{क}$
~~ 32. $x_1, x_2, x_3, x_4, x_5$ अवलोकन अवधारणा के साथ हैं और उनका औसत $म$ और मानक विचलन $एस$ है। अवलोकन $क x_1, क x_2, क x_3, क x_4, क x_5$ का मानक विचलन है
(A) $क+एस$
(B) $\frac{एस}{क}$
(C) $क एस$
(D) $एस$
यहां अधिनियममाचक is वे क्या है, please समझाएं |
- इसमें $x_1, x_2, \ldots x_n$ को $n$ अवलोकन कहा जाता है | $w_i=l x_i+k$ जहां $i=1,2, \ldots n$ के लिए $l$ और $k$ स्थिर हैं| यदि $x_i^{\prime} s$ का औसत 48 है और उनका मानक विचलन 12 है, तो $w_i$ की औसत 55 होती है और $w_i$ का मानक विचलन 15 होता है, तो $l$ और $k$ के मान क्या होने चाहिए
(A) $l=1.25, k=-5$
(B) $l=-1.25, k=5$
(C) $l=2.5, k=-5$
(D) $l=2.5, k=5$
- पहले 10 प्राकृतिक संख्याओं के लिए मानक विचलन है
(A) 5.5
(B) 3.87
(C) 2.97
(D) 2.87
- निम्न संख्याओं पर विचलन की गणितीय विचलन के लिए के बाद 1 जोड़ा जाता है
(A) 6.5
(B) 2.87
(C) 3.87
(D) 8.25
- पहले 10 सकारात्मक पूर्णांकों को गुणा करने के बाद -1 से जोड़ दिया जाता है, उन संख्याओं का वर्यंचन क्या होगा
(A) 8.25
(B) 6.5
(C) 3.87
(D) 2.87
- नमूने के आकार के बारे में निम्नलिखित जानकारी होती है: $60: \quad x^{2}=18000$,
$ x=960 $
तात्कालिक विचलन है
(A) 6.63
(B) 16
(C) 22
(D) 44
- दो वितरणों की गणनीय भेदभाव यदि 50 और 60 है, और उनका गणितीय अंक में अंतर 30 और 25 होता है तो
(A) 0
(B) 1
(C) 1.5
(D) 2.5
- कुछ तापमान आंकड़ों का मानक विचलन ${ }^{\circ} C$ में 5 है। यदि डेटा को ${ }^{\circ} F$ में परिवर्तित किया जाए, तो व्यारियंस क्या होगा?
(A) 81
(B) 57
(C) 36
(D) 25
-
अधिनियममाचक मानक विचलन $=\frac{\cdots}{\text{ माध्यक }} \times 100$
-
यदि $\bar{{}x}$ $x$ के $n$ मानों का माध्यम है, तो $ _{i=1}(x_i-\bar{{}x})$ हमेशा बराबर होता है
यदि $a$ अपने चयन के अलावा $x$ के किसी भी मान का होता है, तो $ _{i=1}^{n}(x_i-\bar{{}x})^{2}$
$(x_i-a)^{2}$ होता है
-
एक डेटा का विचलन 121 होने पर उसका मानक विचलन क्या होता है
-
एक डेटा का मानक विचलन मूल में भरोसेमंद रहता है, लेकिन माप के परिवर्तन पर नहीं
-
मानों की मानक से एकत्र की गई गणनाओं के विचलन के वर्ग जो होता है।
-
डेटा का माध्य से नापों द्वारा नापा जाता है।
-
माध्योन्नति माध्य से गणनाओं के मानसिक विचालन से लिया गया होता है।





