लीनियर प्रोग्रामिंग (Linear Programming)
अध्याय 12
रैखिक प्रोग्रामिंग
12.1 सवाल-सुलभि
~~ 12.1.1 एक अधिकतमीकरण समस्या जो किसी फ़ंक्शन को अधिकतम या न्यूनतम करने की कोशिश करती है, उसे अधिकतमीकरण समस्या कहा जाता है। अधिकतमीकरण समस्या लाभ, उत्पादन आदि का अधिकतमीकरण शामिल कर सकती है या योग्य संसाधनों का न्यूनतमीकरण कर सकती है।
~~ 12.1.2 रैखिक प्रोग्रामिंग समस्या (आरपीपी)
रैखिक प्रोग्रामिंग समस्या दो चरों (उदाहरण के लिए $x$ और $y$) के लिए एक लैनियर फ़ंक्शन (जिसे आदर्श फ़ंक्शन कहा जाता है) के अधिकतमीकरण (अधिकतम / न्यूनतम) के साथ सम्बन्धित होता है, जो लैनियर असमिका सेट (लैनियर बाधाओं के रूप में जाने जाते हैं) को संतुष्ट करते हैं। रैखिक प्रोग्रामिंग समस्या एक विशेष प्रकार की अधिकतमीकरण समस्या है।
~~ 12.1.3 आदर्श फ़ंक्शन लैनियर फ़ंक्शन $Z=a x+b y$, जहां $a$ और $b$ स्थिर हैं, जिसे अधिकतम या न्यूनतम किया जाना है, उसे एक लैनियर आदर्श फ़ंक्शन कहा जाता है।
~~ 12.1.4 निर्णय संख्याओं आदर्श फ़ंक्शन $Z=a x+b y, x$ और $y$ को निर्णय संख्याओं कहा जाता है।
~~ 12.1.5 बाधाएं एक आरपीपी के चरों पर लिनियर असमिकाओं या प्रतिबंध को बाधाओं कहा जाता है। शर्त $x \geq 0, y \geq 0$ को गैर-नकारात्मक प्रतिबंध कहा जाता है।
~~ 12.1.6 संभव्य क्षेत्र एक आरपीपी की सभी बाधाओं, जिसमें अधिकांशतः गैर-नकारात्मक प्रतिबंध $x \geq 0, y \geq 0$ शामिल होती है, द्वारा निर्धारित सामान्य क्षेत्र को संभव्य क्षेत्र कहा जाता है।
~~ 12.1.7 संभव्य हल एक आरपीपी के संभव्य हल कोणों और सीमा पर स्थित बिंदुओं को संभव्य हलों को प्रतिस्थानित करते हैं।
~~ 12.1.8 असंभव्य हल संभव्य क्षेत्र के बाहर का किसी भी बिंदु को असंभव्य हल कहा जाता है।
~~ 12.1.9 आदर्श (संभव्य) हल किसी भी संभव्य क्षेत्र में जो उदारवादी फ़ंक्शन के अधिकतम या न्यूनतम मान (अधिकतम या न्यूनतम) प्रदान करता है, उसे आदर्श हल कहा जाता है।
इनफरमल साधनों को हल करने में ये सिद्धांत मूलभूत हैं।
~~ 12.1.10 प्रमेय 1 एक आरपीपी के लिए संभव्य क्षेत्र $R$ (वक्ता बहुभुज) हो और आदर्श फ़ंक्शन $Z=a x+$ द्वारा विवरणित प्रतिबंध के तहत $y$ हो। जब $Z$ का एक आदर्श मूल्य होता है (अधिकतम या न्यूनतम), जहां $x$ और $y$ तहत प्रतिबंध के द्वारा संघटित होते हैं, तो यह आदर्श मूल्य अवश्य हौंए (कोण) परिपत्र के एक कोने पर पाया जाना चाहिए।
प्रमेय 2 एक आरपीपी के लिए संभव्य क्षेत्र $R$ हो और आदर्श फ़ंक्शन $Z=a x+$ द्वारा विवरणित प्रतिबंध का हो। यदि $R$ सीमित है, तो आदर्श फ़ंक्शन $Z$ के पास $R$ पर एक अधिकारी और एक न्यूनतम मूल्य दोनों होते हैं और इनमें से प्रत्येक एक कंवर्ट परिपत्र के एक कोने पर होते हैं।
यदि संभव्य क्षेत्र $R$ असीमित है, तो आदर्श फ़ंक्शन का अधिकतम या न्यूनतम मूल्य हो सकता है या नहीं हो सकता है। हालांकि, यदि यह मौजूद है, तो यह परिपत्र के एक कोने पर ही होना चाहिए।
12.1.11 निर्धारित बिंदु पद्धति द्वारा एक आरपीपी को हल करना
इस पद्धति में निम्नलिखित चरण शामिल होते हैं:
(1) एलपीपी का संभाव्य क्षेत्र ढूंढें और उस कोण पर स्रेणियों के दो समान्तर रेखाओं को हल करके या उस बिंदु पर उत्पन्न होने वाले या उनसे यौगिक अवशेष करके निर्धारित करें।
(2) प्रति कोण पर उद्देश्य कार्यक्षेत्र को मूल्यांकन करें 〖Z = a x 〗 + के साथ।
M और m को यौगिक अवशेष की सबसे बड़ी और सबसे छोटी मूल्य का उपयोग करें।
(3) (क) यदि संभाव्य क्षेत्र सीमित है, तो M और m प्रत्येक यौगिक अवशेष का अधिकतम और न्यूनतम मूल्य को प्रतिनिधित्व करते हैं।
(ii) मामले में, संभाव्य क्षेत्र असीमित है।
(अ) 〖Z 〗 M, यदि खुली हुई आधा त्रिभुज a x + b y > M यौगिक अवशेष और संभाव्य क्षेत्र के साथ कोई समान बिंदु नहीं है। अन्यथा, Z का अधिकतम मान नहीं होता है।
(ब) इसी तरह, m Z की न्यूनतम मान है, यदि खुली हुई आधा त्रिभुज a x + b y <m यौगिक अवशेष और संभाव्य क्षेत्र के साथ कोई समान बिंदु नहीं है। अन्यथा, Z का न्यूनतम मान नहीं होता है।
~~ 12.1.12 एकाधिक अधिकाधिक समाधान बिंदु यदि संभाव्य क्षेत्र के दो कोण ऐसे आप्त समाधान हैं, अर्थात वे एक ही अधिकतम या न्यूनतम को उत्पन्न करते हैं, तो इन दो कोणों को जोड़ने वाले रेखा सेगमेंट पर कोई भी बिंदु भी उसी प्रकार का आप्त समाधान होगा।
12.2 संदर्भित उदाहरण
संक्षेप में उत्तर (S.A.)
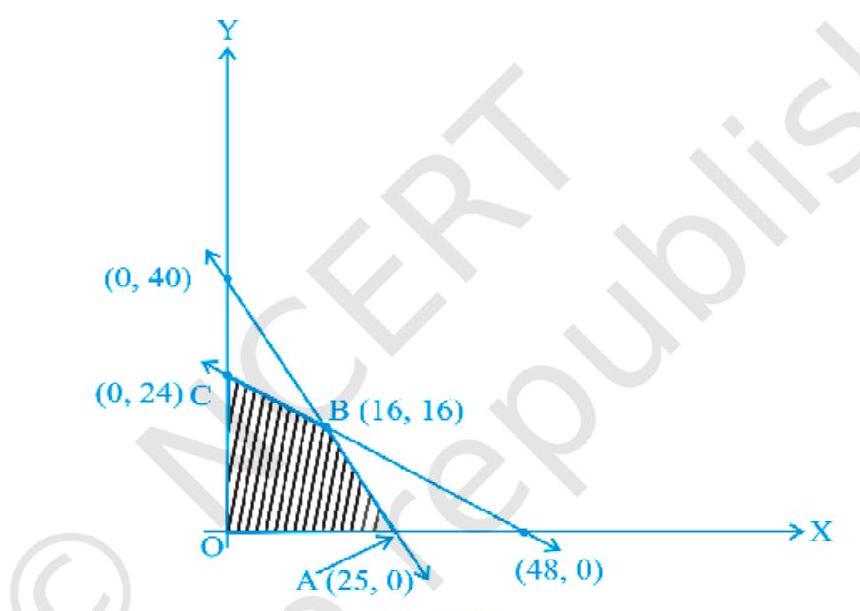
~~ उदाहरण 1 यदि एक एलपीपी के लिए संभाव्य क्षेत्र चित्रित है, तो Z=4 x+3 य की अधिकतम मान ढूंढें।
समाधान संभाव्य क्षेत्र सीमित है। इसलिए, Z की अधिकतम मान संभाव्य क्षेत्र के कोण पर होना चाहिए।
| कोण बिंदु | Z का मान | |
|---|---|---|
| O,(0,0) | 4(0)+3(0)=0 | |
| A(25,0) | 4(25)+3(0)=100 | |
| B(16,16) | 4(16)+3(16)=\mathbf{1 1 2} | $\leftarrow \text{(अधिकतम)}$ |
| C(0,24) | 4(0)+3(24)=72 |
इसलिए, Z का अधिकतम मान 112 है।
चित्र 12.1
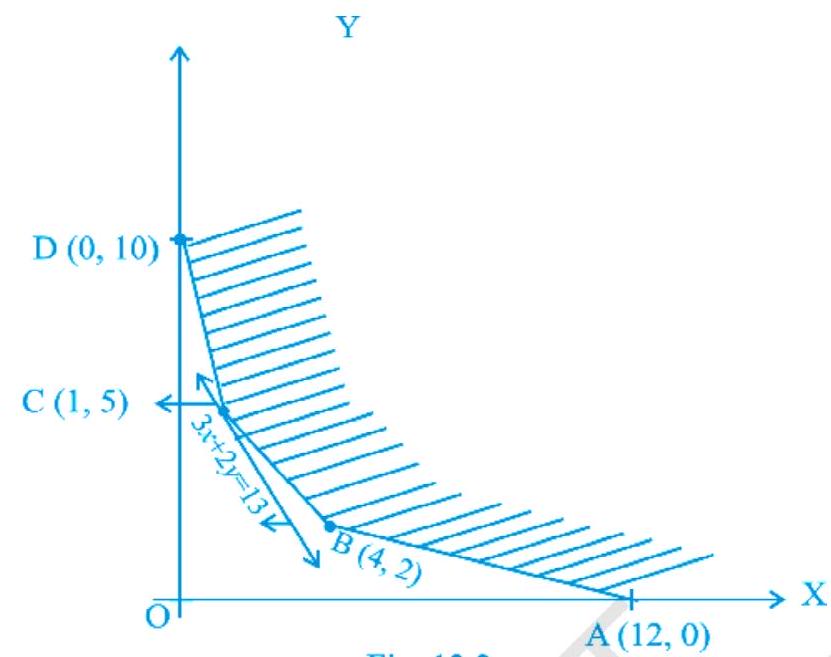
~~ उदाहरण 2 यदि एक एलपीपी के लिए संभाव्य क्षेत्र चित्रित है, तो Z=3 x+2 य की न्यूनतम मान ढूंढें।
समाधान संभाव्य क्षेत्र (R) असीमित है। इसलिए Z की न्यूनतम मान हो सकता है या नहीं हो सकता है। यदि उत्पन्न होता है, तो यह संभाव्य क्षेत्र के कोण पर होगा।
| कोण बिंदु | Z का मान | |
|---|---|---|
| A, (12, 0) | 3(12)+2(0)=36 | |
| B (4, 2) | 3(4)+2(2)=16 | |
| C (1, 5) | 3(1)+2(5)=\mathbf{1 3}$ | $\leftarrow \text{(न्यूनतम)}$ |
| D (0, 10) | 3(0)+2(10)=20 |
चित्र 12.2
हम 〖3 x+2 y<13 〗 का ग्राफ बनाते हैं। हम देखते हैं कि 3 x+2 y<13 और R द्वारा खुली हुई आधा त्रिभुज का कोई साझा बिंदु नहीं है। इसलिए, 13 का सबसे छोटा मान Z का न्यूनतम मान है।
~~ उदाहरण 3 निम्नलिखित LPP को ग्राफिक रूप से हल करें:
$Z=2 x+3 य$ का अधिकतम करें,
बाध्य हो $x+y ≤ 4, x ≥ 0, y ≥ 0$
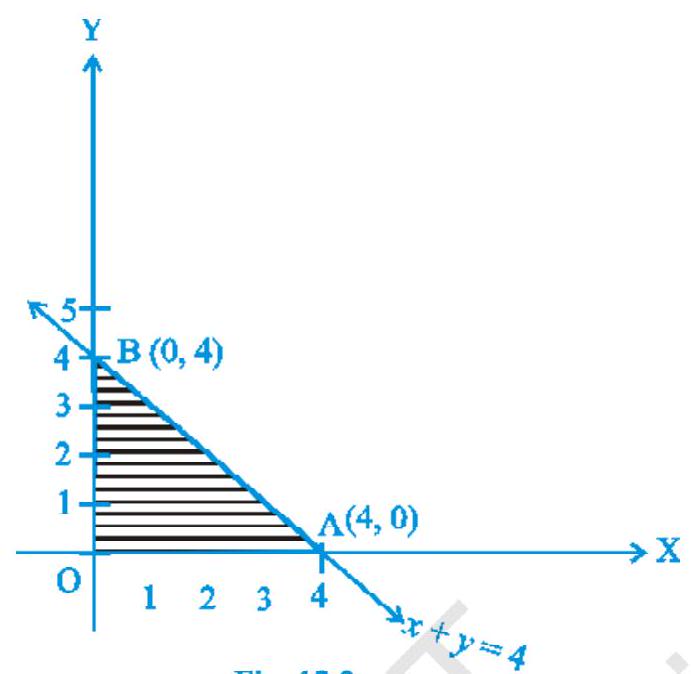
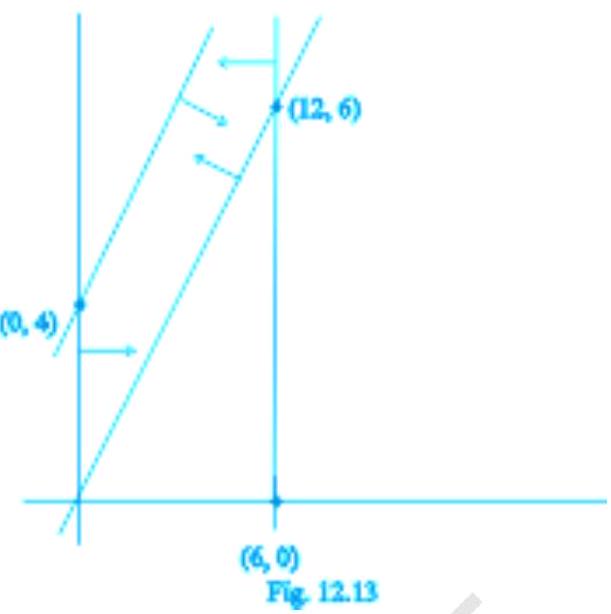
समाधान चित्र 12.3 के लिए (OAB) छाया भाग एक संभाव्य क्षेत्र है जिसे $x ≥ 0, y ≥ 0$ और $x+y ≤ 4$ की आवाज से निर्धारित किया गया है।
व्यवहार्य क्षेत्र $OAB$ सीमित है, इसलिए, व्यवहार्य क्षेत्र के कोने बिंदु में अधिकतम मान होगा।
कोने बिंदु यहां होते हैं $O(0,0), A(4,0)$ और $B(0,4)$।
प्रत्येक कोने बिंदु पर $Z$ की मूल्यांकन करें।
| कोने बिंदु | Z का मान | |
|---|---|---|
| $0,(0,0)$ | $2(0)+3(0)=0$ | |
| A $(4,0)$ | $2(4)+3(0)=8$ | |
| B $(0,4)$ | $2(0)+3(4)=\mathbf{1 2}$ | $\leftarrow \text{अधिकतम}$ |
चित्र, 12.3
इसलिए, $Z$ का अधिकतम मान 12 है परिक्रमा $(0,4)$ पर
~~ उदाहरण 4 एक विनिर्माण कंपनी दो प्रकार के टेलीविजन सेट बनाती है; एक काला और सफेद और दूसरा रंगीन है। कंपनी के पास हफ्ते में अधिकतम 300 सेट तैयार करने के लिए संसाधन हैं। एक काला और सफेद सेट तैयार करने में 1800 रुपये लगते हैं और रंगीन सेट बनाने में 2700 रुपया लगता है। कंपनी 648000 रुपये सप्ताह में टेलीविजन सेट बनाने के लिए अधिकतम खर्च कर सकती है। इसके प्रति रंगीन सेट प्रति 510 रुपया का लाभ होता है और सफेद सेट प्रति 675 रुपया का लाभ होता है, तो कब तक कंपनी को अधिकतम लाभ होगा कि दोनों प्रकार के सेट के कितने सेट बनाए जाएं। उपयोग करने के लिए इस समस्या को लीनियर प्रोग्रामिंग समस्या बनाएं इसका उदाहरण देकर कि उद्देश्य है लाभ का अधिकतम निर्धारित करना।
समाधान को करें। $x$ और $y$ को प्रति हफ्ते बनाए गए सफेद और संगीत सेटों की गणना करें। इस प्रकार
$ \quad \quad x \geq 0, y \geq 0 $
क्योंकि कंपनी हफ्ते में अधिकतम 300 सेट तैयार कर सकती है, इसलिए,
$ \quad \quad x+y \leq 300 $
एक सेट का हफ्तावारी लागत (रुपये में)
$ \quad \quad 1800 x+2700 y $
और कंपनी 648000 रुपये तक खर्च कर सकती है। इसलिए,
$ \quad \quad 1800 x+2700 y \leq 648000 \text{, यानी, या } 2 x+3 y \leq 720 $
$x$ सफेद और $y$ रंगीन सेटों पर कुल लाभ रुपये $(510 x+675 y)$ होता है।लेट $Z=510 x+675 y$. यह है उद्देश्य समाधान।
इस प्रकार, समस्या का गणितीय समाधान निम्नलिखित है
$अधिकतम होने के लिए Z=510 x+675 y का*
प्रतिबंध: $कटौती के नियम:* $ x+y \leq 300** 2 x+3 y \leq 720 *\ x \geq 0, y \geq 0**
चित्र. 12.4
लम्बा उत्तर (L.A.)
~~ उदाहरण 5 उदाहरण 4 का संदर्भ देखें। LPP को हल करें।
समाधान समस्या है: Z को $510 x+675 y$ से अधिकतम करो
बाधाएं : $ \begin{rcases} x+y \leq 300 \\ 2 x+3 y \leq 720 \\ x \geq 0, y \geq 0 \end{rcases} $
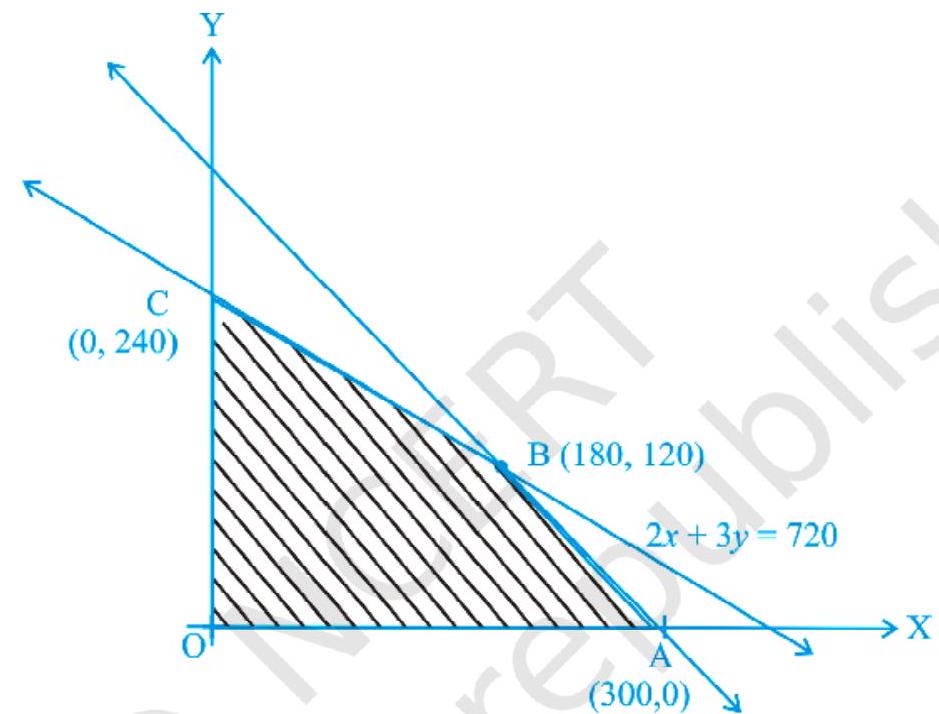
व्यवहार्य क्षेत्र OABC चित्र. 12.4 में दिखाया गया है।
व्यवहार्य क्षेत्र सीमित होने के कारण, यहां Z का अधिकतम होना चाहिए OBC के कोने बिंदु पर।
| कोने बिंदु | Z का मान | |
|---|---|---|
| O (0, 0) | $510(0)+675(0)=0$ | |
| A (300, 0) | $510(300)+675(0)=153000$ | |
| B (180, 120) | $510(180)+675(120)=\mathbf{1 7 2 8 0 0}$ | $\leftarrow \text{अधिकतम}$ |
| C (0, 240) | $510(0)+675(240)=162000$ |
अतः, अधिकतम $Z$ 172800 है पॉइंट $(180,120)$ पर, अर्थात उधम को 180 काले और सफेद टेलीविजन सेट और 120 रंगीन टेलीविजन सेट उत्पादित करना चाहिए ताकि अधिकतम लाभ मिल सके।
~~ उदाहरण 6 न्यूनतमीकरण करें $Z=3 x+5 y$ इसकी प्रतिबंधिताओं के अधीन:
$ \begin{aligned} & x+2 y \geq 10 \\ & x+y \geq 6 \\ & 3 x+y \geq 8 \\ & x, y \geq 0 \end{aligned} $
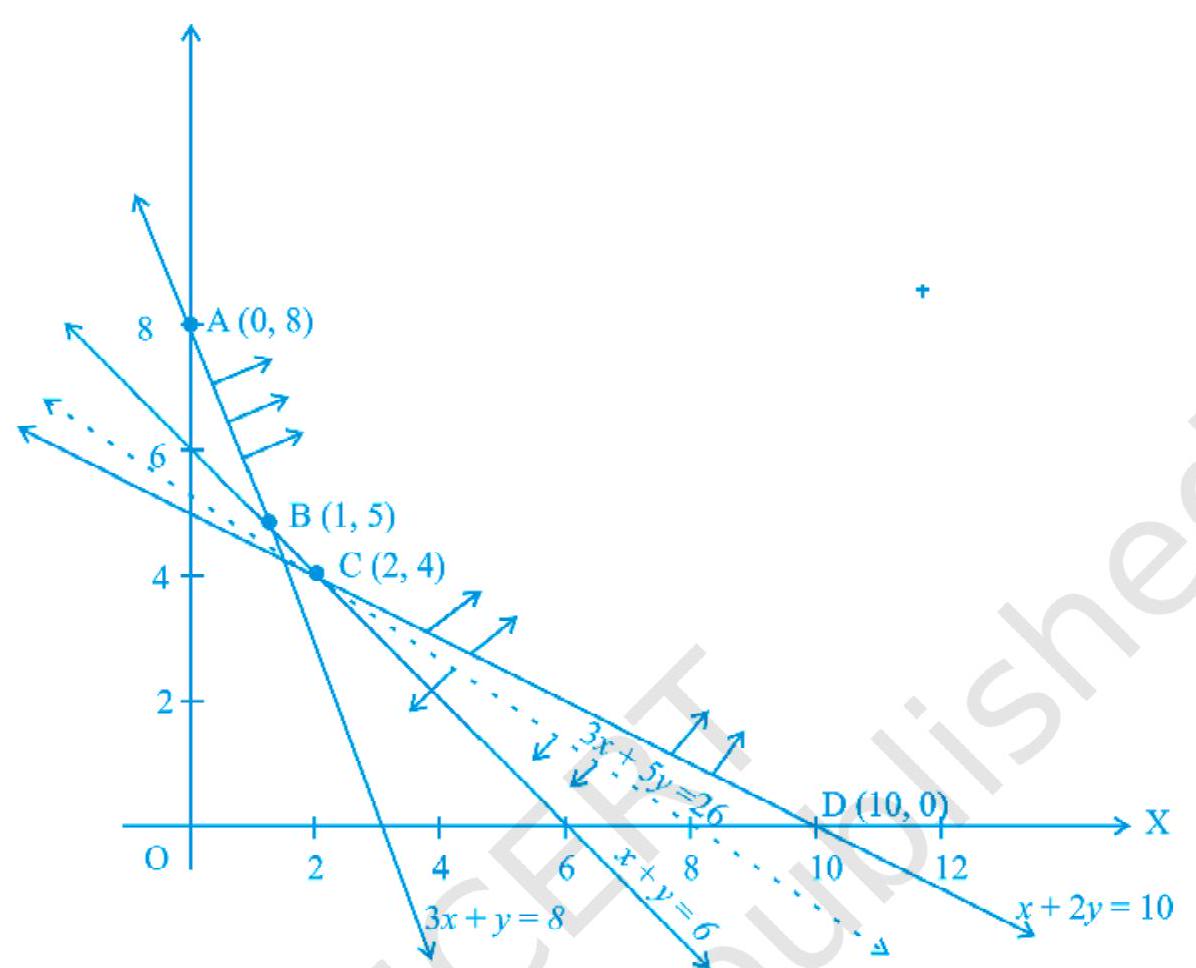
समाधान हम पहले $x+2 y=10, x+y=6,3 x+y=8$ के ग्राफ खींचते हैं। छायांकित क्षेत्र $A B C D$ ऊपर दिए गए बाधाओं द्वारा निर्धारित अवधियों (R) द्वारा निर्धारित फ़ीज़िबल क्षेत्र है। दृष्टिगत क्षेत्र असीमित है। इसलिए, Z की न्यूनतम राशि हो सकती है या नहीं हो सकती है। अगर यह होता है, तो यह कर्ण पॉइंट पर होगा।
| कॉर्नर पॉइंट | Z की मान | |
|---|---|---|
| A (0,8) | 40 | |
| B (1,5) | 28 | |
| C (2,4) | $\mathbf{2 6}$ | $\leftarrow \text{सबसे छोटा}$ |
| D (10,0) | 30 |
चित्र 12.5
हम चित्र 12.5 में पुंकज रेखा द्वारा प्रशांत लाइन $3 x+5 y<26$ के ग्राफ खींचते हैं।
हम देखते हैं कि प्रशांत पूलेक्षी $3 x+5 y<26$ और $R$ द्वारा निर्धारित, खुली हुई आधी तलवार के क्षेत्र में कोई साझा पॉइंट नहीं है। अतः, 26 Z की न्यूनतम मान है।
उदाहरण प्रकार के प्रश्न
उदाहरण 7 से 8 में दी गई चार विकल्पों में से सही उत्तर चुनें।
~~ उदाहरण 7 सीमा पॉइंट्स व्यवस्था द्वारा निर्धारित फ़ीज़िबल क्षेत्र के हैं $(0,10),(5,5),(15,15),(0,20)$. लेट $Z=p x+q y$, $p, q>0$. $Z$ का अधिकतम इंद्रधनुष किंवदंति $(15,15)$ और $(0,20)$ पर होने के लिए p और q पर निर्भरता है
(A) $p=q$
(B) $p=2 q$
(C) $q=2 p$
(D) $q=3 p$
समाधान सही उत्तर (D) है। क्योंकि Z $(15,15)$ और $(0,20)$ पर अधिकतम होता है, इसलिए $15 p+15 q=0 . p+20 q \Rightarrow q=3 p$।
उदाहरण 8 एलपीपी के लिए फैज़िब्ल क्षेत्र (ढलवान) चित्र 14.6 में दिखाया गया है। $Z=4 x+3 y$ का न्यूनतम मान बिंदु पर होता है
(A) $(0,8)$
(B) $(2,5)$
(C) $(4,3)$
(D) $(9,0)$
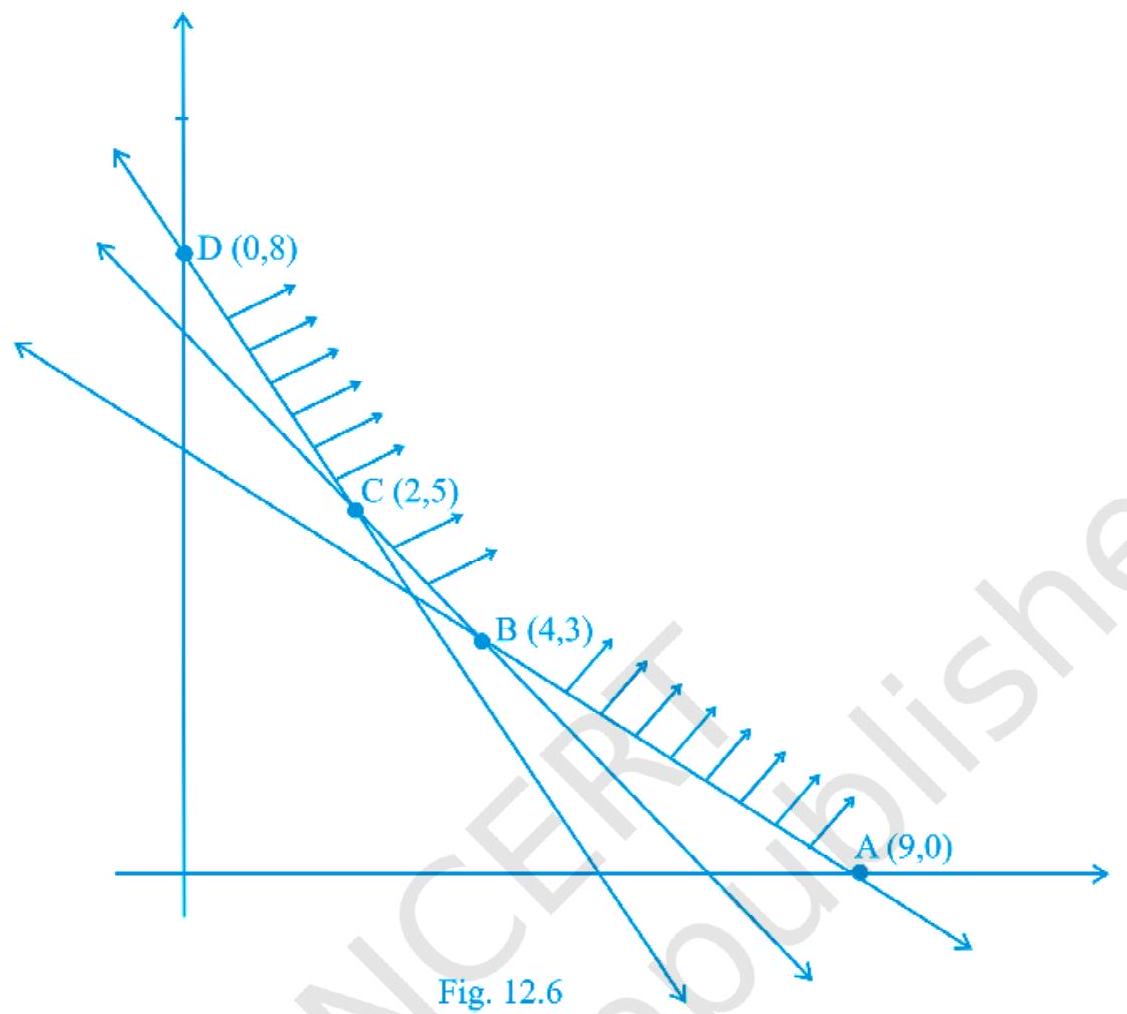
समाधान सही उत्तर (B) है।
हर उदाहरण 9 और 10 में रिक्त स्थान भरें:
उदाहरण 9 एक LPP में, जो लीनियर कार्य होना चाहिए, जिसे अधिकतम या न्यूनतम निश्चित करना होता है, वह एक लिनियर__________कार्य कहलाता है।
समाधान ग्राहक.
उदाहरण 10 एक LPP के सभी लीनियर प्रतिबंधों द्वारा निर्धारित साधारण क्षेत्र को कहा जाता है___________क्षेत्र।
समाधान फ़ीज़िबल.
क्या उदाहरण 11 और 12 के कथन सही हैं या गलत हैं।
उदाहरण 11 यदि लीनियर प्रोग्रामिंग समस्या के लिए फ़ीज़िबल क्षेत्र सीमित है, तो उद्देश्य समाधान Z=ax+by पर R पे एक अधिकतम और एक न्यूनतम मान होगा।
समाधान सही
उदाहरण 12 एक लीनियर प्रोग्रामिंग समस्या में उद्देश्य समाधान Z=ax+by की न्यूनतम मुल्य एक से अधिक सीमांक पॉइंट पर हमेशा होती है।
समाधान गलत
न्यूनतम मूल्य एक से अधिक सीमांक पॉइंट पर भी हो सकता है।
12.3 व्यायाम
संक्षेपित उत्तर (S.A.)
~~ 1. $Z=11 x+7 y$ की अधिकतम मानयुक्ति निर्धारित करें, बाधाओं के अनुसार: $2 x+y \leq 6, x \leq 2, x \geq 0, y \geq 0$।
~~ 2. $Z=3 x+4 y$ का अधिकतम मानयुक्ति निर्धारित करें, बाधाओं के अनुसार: $x+y \leq 1, x \geq 0, y \geq 0$।
~~ 3. निर्धारित करें कि वक्रीयता $Z=11 x+7 y$ की अधिकतम मानयुक्ति, बाधाओं के अनुसार: $x \leq 3, y \leq 2$, $x \geq 0, y \geq 0$।
~~ 4. $Z=13 x-15 y$ की न्यूनतम मानयुक्ति निर्धारित करें, बाधाओं के अनुसार: $x+y \leq 7,2 x-3 y+6 \geq$ $0, x \geq 0, y \geq 0$।
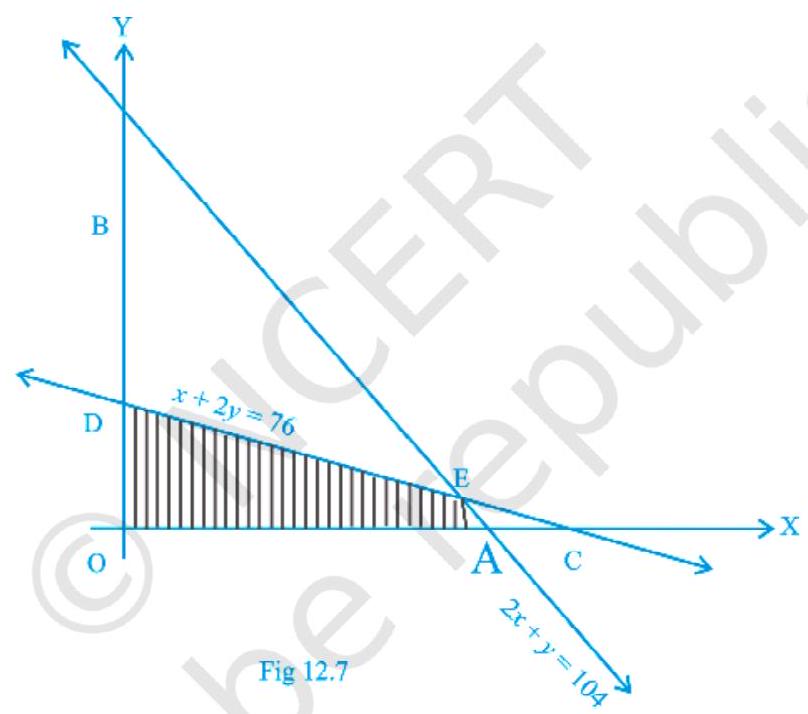
~~ 5. निर्धारित करें कि LPP के लिए संभावित क्षेत्र (ढली हुई) की अधिकतम मानयुक्ति $Z=3 x+4 y$ क्या है, यदि इसका चित्र 12.7 में दिखाया गया है।
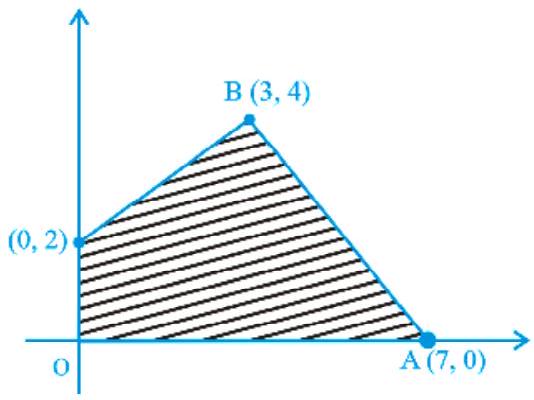
~~ 6. LPP के लिए संभावित क्षेत्र (ढली हुई) का चित्र 12.8 में दिखाया गया है।
$Z=5 x+7 y$ की अधिकतम मानयुक्ति निर्धारित करें।
चित्र 12.8
~~ 7. LPP के लिए संभावित क्षेत्र को चित्र 12.9 में दिखाया गया है। $Z=11 x+7 y$ का न्यूनतम मानयुक्ति खोजें।
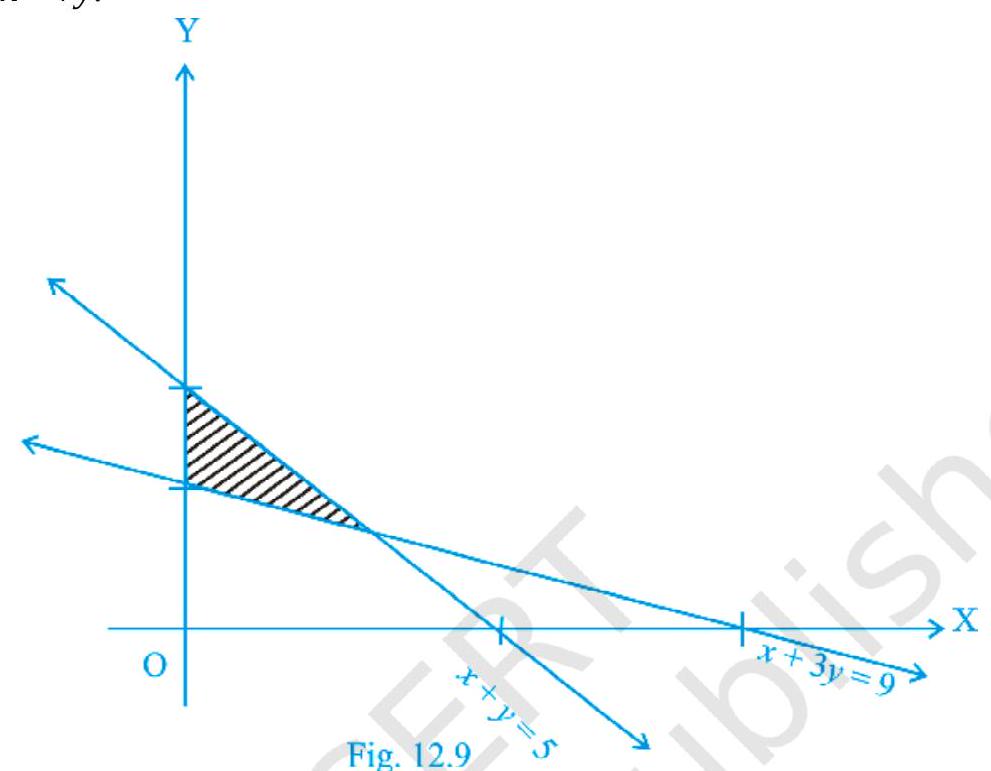
~~ 8. उपरोक्त व्यायाम 7 में संदर्भित करें। $Z$ की अधिकतम मानयुक्ति खोजें।
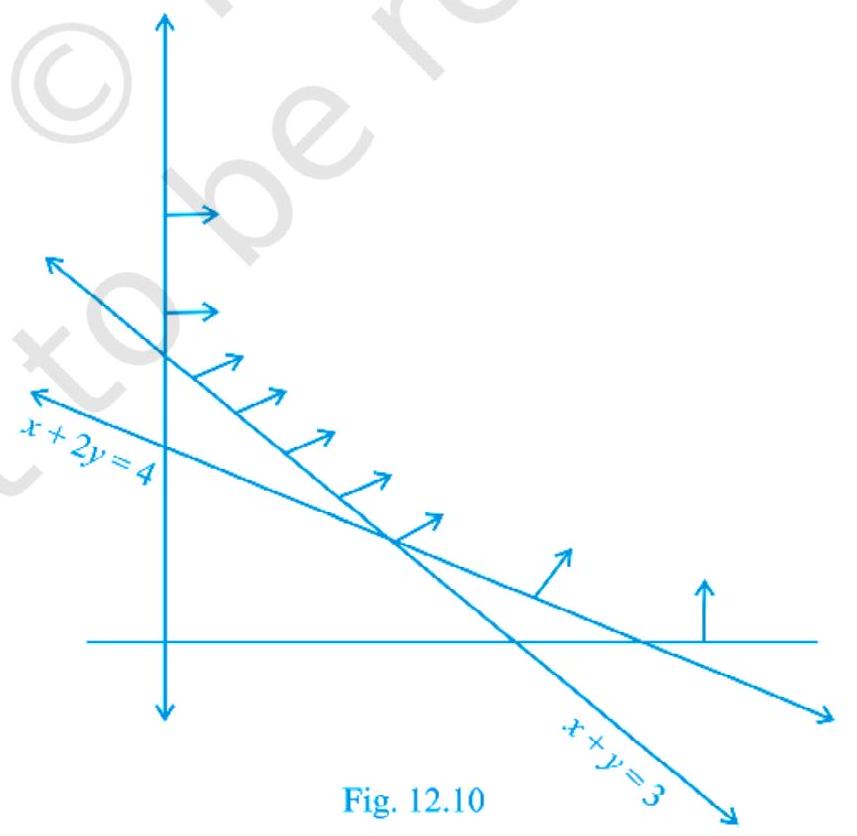
~~ 9. LPP के लिए संभावित क्षेत्र को चित्र 12.10 में दिखाया गया है। इस क्षेत्र के हर कोने बिन्दु पर $Z=4 x+y$ का मूल्यांकन करें। $Z$ की न्यूनतम मानयुक्ति खोजें, यदि यह मौजूद हो।
~~ 10. चित्र 12.11 में, LPP के लिए संभावित क्षेत्र (ढली हुई) दिखाया गया है। $Z=x+2 y$ की अधिकतम और न्यूनतम मानयुक्ति निर्धारित करें।
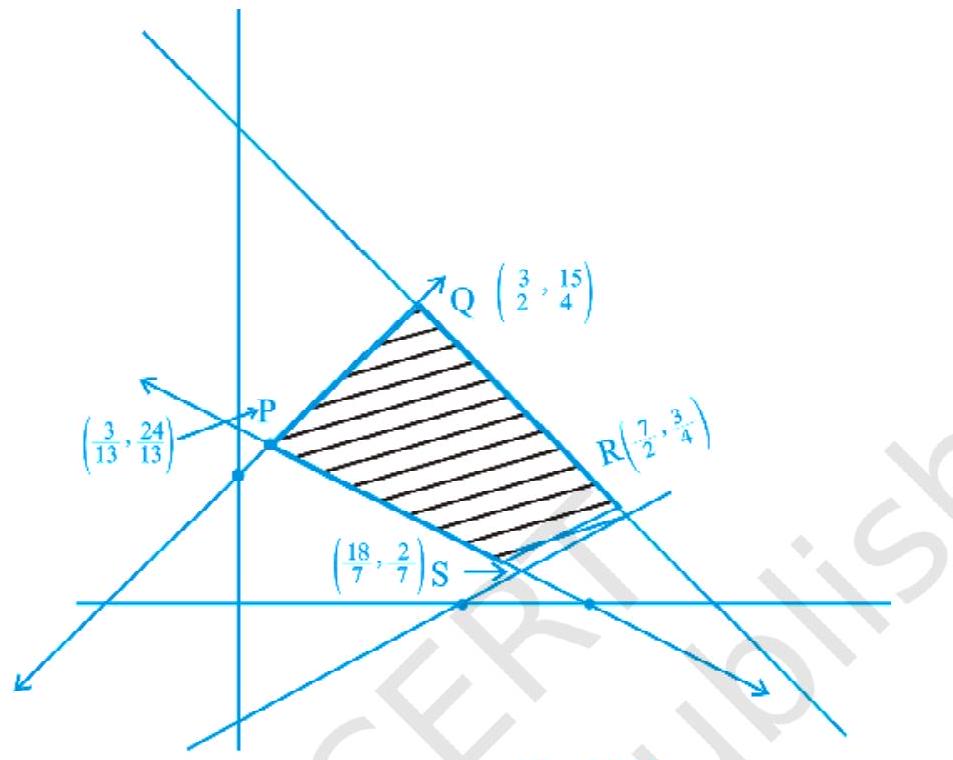चित्र 12.11
~~ 11. इलेक्ट्रॉनिक सर्किटों के निर्माता के पास 200 रेजिस्टर, 120 ट्रांजिश्टर और 150 कैपैसिटर के स्टॉक है, और उसको दो प्रकार के सर्किट A और B बनाने की आवश्यकता है। प्रकार A में 20 रेजिस्टर, 10 ट्रांजिस्टर और 10 कैपैसिटर की आवश्यकता होती है। प्रकार B में 10 रेजिस्टर, 20 ट्रांजिस्टर और 30 कैपैसिटर की आवश्यकता होती है। प्रकार A सर्किट पर लाभ Rs 50 होता है और प्रकार B सर्किट पर लाभ Rs 60 होता है, निर्माता अपनी लाभ मान्यता मैक्सिमाइज़ कर सके।
~~ 12. एक कंपनी को 1200 पैकेज वान के माध्यम से परिवहन करने की आवश्यकता है जो प्रत्येक वान में 200 पैकेज को ले सकता है और छोटे वान में हर वान में 80 पैकेज धारण कर सकता है। प्रत्येक बड़े वान के लिए नियुक्त करने का खर्च Rs 400 है और प्रत्येक छोटे वान के लिए Rs 200 है। काम पर केवल Rs 3000 खर्च किए जा सकते हैं और बड़े वान की संख्या छोटे वान की संख्या से अधिक नहीं हो सकती। इसे एक LPP के रूप में सारगर्भित करें जिसमें उद्देश्य लागत को कम से कम करना है।
13. एक कंपनी दो प्रकार के स्क्रू ए और बी बनाती है। सभी स्क्रूस एक थ्रेडिंग मशीन और एक स्लॉटिंग मशीन से गुजरने होते हैं। टाइप ए स्क्रू का एक बॉक्स थ्रेडिंग मशीन पर 2 मिनट और स्लॉटिंग मशीन पर 3 मिनट का समय लेता है। टाइप बी स्क्रू का एक बॉक्स थ्रेडिंग मशीन पर 8 मिनट और स्लॉटिंग मशीन पर 2 मिनट का समय लेता है। एक हफ्ते में, प्रत्येक मशीन के लिए 60 घंटे उपलब्ध होते हैं।
इन स्क्रूस को बेचते हुए, कंपनी को प्रति टाइप ए स्क्रू बॉक्स पर 100 रुपये और प्रति टाइप बी स्क्रू बॉक्स पर 170 रुपये का लाभ मिलता है।
लाभ को अधिकतम करने के लिए, इस समस्या को एक लिनियर प्रोग्रामिंग समस्या के रूप में सूचीबद्ध करें।
~~ 14. एक कंपनी दो प्रकार के स्वेटर निर्मित करती है: प्रकार ए और प्रकार बी। प्रकार ए स्वेटर बनाने की लागत 360 रुपये होती है और प्रकार बी स्वेटर बनाने की लागत 120 रुपये होती है। कंपनी अधिकतम 300 स्वेटर बना सकती है और अधिकतम 72,000 रुपये प्रतिदिन खर्च कर सकती है। प्रकार बी के स्वेटरों की संख्या प्रकार ए के स्वेटरों की संख्या से अधिकतर 100 तक कम होना चाहिए। प्रकार ए के हर स्वेटर के लिए कंपनी को 200 रुपये और प्रकार बी के हर स्वेटर के लिए 120 रुपये का लाभ मिलता है।
लाभ को अधिकतम करने के लिए, इस समस्या को एक लिनियर प्रोग्रामिंग समस्या के रूप में सूचीबद्ध करें।
~~ 15. एक आदमी अपनी मोटरसाइकिल पर $50 \ km / घंटा$ की गति से चलता है। उसे पेट्रोल पर $2 ₹ / km$ का खर्च आना पड़ता है। यदि वह उसे $80 \ km / घंटा$ की गति से चलाए, तो पेट्रोल का खर्च $3 ₹ / km$ हो जाता है। उसके पास पेट्रोल पर अधिकतम 120 रुपये और एक घंटे का समय होता है। वह अधिकतम दूरी ढूंढ़ना चाहता है।
इस समस्या को एक लिनियर प्रोग्रामिंग समस्या के रूप में व्यक्त करें।
लंबा उत्तर (ला.)
~~ 16. अभ्यास 11 के संदर्भ में देखें। निर्माता को अपने लाभ को अधिकतम करने के लिए कितने प्रकार A के सर्किट और B के सर्किट निर्मित करने चाहिए? अधिकतम लाभ की गणना करें।
~~ 17. अभ्यास 12 के संदर्भ में देखें। न्यूनतम लागत क्या होगी?
~~ 18. अभ्यास 13 के संदर्भ में देखें। लिनियर प्रोग्रामिंग समस्या को हल करें और निर्माता को अधिकतम लाभ निर्धारित करें।
~~ 19. अभ्यास 14 के संदर्भ में देखें। कंपनी को प्रतिदिन अधिकतम लाभ प्राप्त करने के लिए प्रत्येक प्रकार के स्वेटर की संख्या कितनी होनी चाहिए? अधिकतम लाभ क्या होगा।
~~ 20. अभ्यास 15 के संदर्भ में देखें। आदमी कितनी अधिकतम दूरी यात्रा कर सकता है।
~~ 21. $Z=x+y$ को अधिकतम बनाएँ, जबकि $x+4y \leq 8,2x+3y \leq 12,3x+y \leq 9, x \geq 0, y \geq 0$।
~~ 22. एक निर्माता निम्नलिखित मॉडल के दो बाइक निर्मित करता है - मॉडल X और मॉडल Y। मॉडल X के लिए प्रति इकाई 6 मन-घंटा लगते हैं, जबकि मॉडल Y के लिए प्रति इकाई 10 मन-घंटा लगते हैं। हर हफ्ते 450 मन-घंटा उपलब्ध होते हैं। हैंडलिंग और मार्केटिंग लागत मॉडल X और मॉडल Y के लिए यौगिक रूप से 2000 और 1000 रुपये प्रति इकाई होती हैं। इन कारणों के लिए कुल धन उपलब्धि प्रतिसप्ताह 80,000 रुपये है। मॉडल X और मॉडल Y के प्रति इकाई लाभ 1000 और 500 रुपये है। ताकि निर्माता कितनी बाइकों को निर्मित करें ताकि अधिकतम लाभ मिले? अधिकतम लाभ निर्धारित करें।
~~
23. रोजाना आहार को पूरक करने के लिए, एक व्यक्ति को $X$ और $Y$ गोलियों को लेना चाहता है। $X$ और $Y$ में आयरन, कैल्शियम और विटामिन की सामग्री (मिलीग्राम प्रति गोली) नीचे दी गई है:
| गोलियाँ | आयरन | कैल्शियम | विटामिन |
|---|---|---|---|
| $X$ | 6 | 3 | 2 |
| $Y$ | 2 | 3 | 4 |
व्यक्ति को कम से कम 18 मिलीग्राम आयरन, 21 मिलीग्राम कैल्शियम और 16 मिलीग्राम विटामिन की आवश्यकता है। $X$ और $Y$ की प्रति गोली की कीमत रुपये 2 और 1 है। इन परियोजनाओं की कितनी गोलियों को व्यक्ति को दैनिक आवश्यकता को पूरा करने के लिए लेना चाहिए ताकि उपरोक्त आवश्यकता को कम से कम खर्च में पूरा किया जा सके?
~~ 24. एक कंपनी तीन प्रकार के कैलकुलेटर बनाती है: A, B और C, प्रकार I और प्रकार II में। कंपनी को A प्रकार के कम से कम 6400 कैलकुलेटर, B प्रकार के 4000 कैलकुलेटर और C प्रकार के 4800 कैलकुलेटर के आदेश हैं। प्रकार I में, हर दिन 50 A प्रकार के कैलकुलेटर, 50 B प्रकार के और 30 C प्रकार के बनाए जाते हैं; प्रकार II में, हर दिन 40 A प्रकार के कैलकुलेटर, 20 B प्रकार के और 40 C प्रकार के बनाए जाते हैं। उपकरण I और II को संचालित करने के लिए रुपये 12000 और 15000 रुपए प्रतिदिन खर्च होते हैं। ऑपरेटिंग लागत को कम से कम करने और मांग पूरी करने के लिए प्रति कारख़ाने को कितने दिनों तक संचालित करना चाहिए?
~~ 25. $Z=3 x-4 y$ को अधिकतम और न्यूनतम करें
तारीखीय प्रकार से प्राप्त चार विकल्पों में से सही उत्तर चुनें Exercises 26 से 34 तक में से प्रत्येक में से दिए गए चार विकल्पों में से सही ज़रीया का चयन करें।
~~ 26. सरल बाधाओं संक्रमित संभावना की कोने बिंदुओं $(0,0),(0,40),(20,40),(60,20),(60,0)$ हैं। उद्देश्य फ़ंक्शन के रूप में $Z=4 x+3 y$ है।
कॉलम ए में मात्रा और कॉलम बी में मात्रा का तुलना करें
$\begin{matrix} & \text{कॉलम ए} && \hspace {20mm} \text{कॉलम बी}\\ & \text{Z का अधिकतम} && \hspace {20mm} 324 \end{matrix}$
(A) कॉलम ए में मात्रा अधिक है
(B) कॉलम बी में मात्रा अधिक है
(C) दो मात्राएँ समान हैं
(D) दिए गए जानकारी के आधार पर संबंध नहीं तय किया जा सकता है
~~ 27. एक LPP के लिए संभावित हल चित्र में दिखाया गया है। $Z=3 x-4 y$
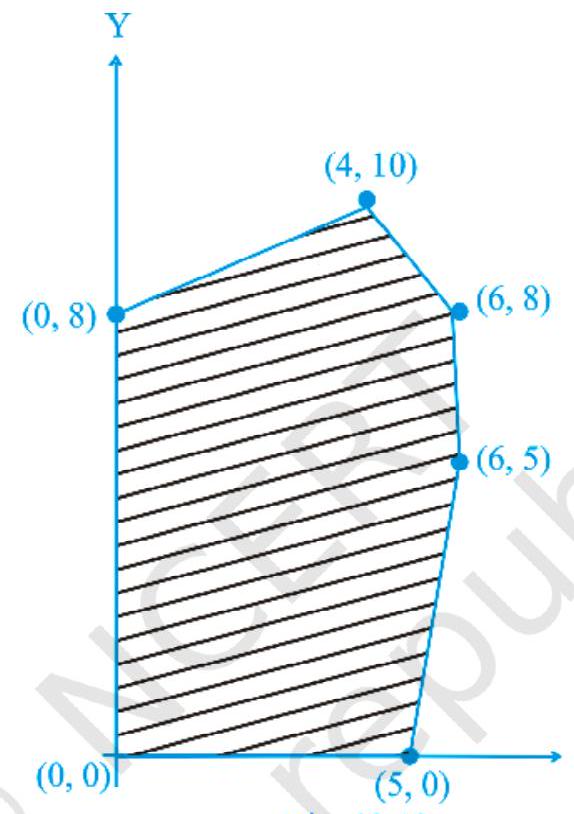चित्र 12.12
$वास्तविक$ $मान$ का न्यूनतम होता है
(A) $(0,0)$
(B) $(0,8)$
(C) $(5,0)$
(D) $(4,10)$
~~ 28. उपकरण 27 का उल्लेख करें। $Z$ की अधिकतम मान होता है
(A) $(5,0)$
(B) $(6,5)$
(C) $(6,8)$
(D) $(4,10)$
~~ 29. उपकरण 27 का उल्लेख करें। ($Z$ की अधिकतम मान + $Z$ की न्यूनतम मान) बराबर है
(A) 13
(B) 1
(C) -13
(D) -17
~~ 30. एक LPP के लिए संभावित क्षेत्र चित्र में दिखाया गया है। $F=3 x-4 y$ $F$ का अधिकतम मान होता है।
(A) 0
(B) 8
(C) 12
(D) -18
~~
31. अभ्यास 30 को देखें। $F$ की न्यूनतम मान है
(A) 0
(B) -16
(C) 12
(D) मौजूद नहीं है
~~ 32. LPP के लिए संभाव्य क्षेत्र के कोने बिंदुओं को $(0,2), (3,0), (6,0), (6,8)$ और $(0,5)$ माना जाता है।
वस्तुनिष्ठ समस्या को $F = 4 x+ 6 y$ कोई वस्तुनिष्ठ करने वाला समाधान होता है।
$F$ की न्यूनतम मान होता है
(A) $(0,2)$ केवल
(B) $(3,0)$ केवल
(C) बिन्दु $(0,2)$ और $(3,0)$ को जोड़ने वाले रेखांक के बीच का मध्य-बिन्दु केवल
(D) बिंदु $(0,2)$ और $(3,0)$ को जोड़ने वाले रेखांक के बीच का कोई भी बिंदु।
~~ 33. अभ्यास 32 को देखें, $F-$ की न्यूनतम मान - न्यूनतम मान =
(A) 60
(B) 48
(C) 42
(D) 18
~~ 34. लैनियर बाधाओं की प्रणाली द्वारा निर्धारित संभावित क्षेत्र के कोने बिंदुओं को $(0,3), (1,1)$ और $(3,0)$ माना जाता है। $Z = p x + q y$ हो, जहां $p, q > 0$। $(3,0)$ और $(1,1)$ पर $Z$ की न्यूनतम मान होने की शर्त है
(A) $p = 2q$
(B) $p = \frac{q}{2}$
(C) $p = 3q$
(D) $p = q$
प्रत्येक अभ्यास में रिक्त स्थान भरें
~~ 35. एलपीपी में चुनिंदा बिंदुओं पर लैनियर असमिकाओं या वर्णन को______ कहा जाता है।
~~ 36. एलपीपी में वस्तुनिष्ठ फ़ंक्शन हमेशा____________ होती है।
~~ 37. एलपीपी के लिए संभावित क्षेत्र____ है तो वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ का अधिकतम मूल्य संभवतः हो सकता है या न हो सकता है।
~~ 38. एलपीपी में यदि वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ का सर्वोच्च मान दोनों संभावित क्षेत्र के कोने बिंदुओं पर समान होता है, तो इन दोनों बिंदुओं को जोड़ने वाले रेखांक पर हर बिंदु एक ही__________ मान देता है।
~~ 39. यदि एक संख्या में बंदहुआ किए गए संख्या कोंजीले में समाहित किया जा सकता है, तो संभावित क्षेत्र को ______ माना जाता है।
~~ 40. एक वस्तुनिष्ठ क्षेत्र का एक कोना वह दो बाउंडरी रेखाओं की ________ होता है जो संभावित क्षेत्र में हैं।
~~ 41. एलपीपी के लिए संभावित क्षेत्र हमेशा एक________ बहुभुज होता है।
अभ्यास 42 से 45 में क्या प्रवक्तान सच्चे (S) या असत्य (A) हैं।
~~ 42. यदि एलपीपी के लिए संभाव्य क्षेत्र बेसीमित है, तो वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ का अधिकतम या न्यूनतम मान संभवतः हो सकता है या नहीं हो सकता है।
~~ 43. एलपीपी में वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ का अधिकतम मान एकमात्र केवल एक संभावित क्षेत्र के कोने बिंदु पर होता है।
~~ 44. एलपीपी में, यदि मूल बिंदु संभावित क्षेत्र का एक पुर्नकोण है, तो वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ की न्यूनतम मान हमेशा 0 होता है।
~~ 45. एलपीपी में, वस्तुनिष्ठ फ़ंक्शन $Z = a x + b y$ का अधिकतम मान हमेशा सीमित होता है।
समाधान
~~ 1. 42
~~ 2. 4
~~ 3. 47
~~ 4. -30
~~ 5. 196
~~ 6. 43
~~ 7. 21
~~ 8. 47
~~ 9. न्यूनतम मान = 3
~~ 10. अधिकतम = 9, न्यूनतम = 3 1/7
~~ 11. अधिकतम करें $Z = 50 x + 60 y$, को करें, उपेक्षा करें:
$2 x + y \leq 20, x + 2 y \leq 12, x + 3 y \leq 15, x \geq 0, y \geq 0$
~~ 12. न्यूनतम करें $Z = 400 x + 200 y$, को करें, उपेक्षा करें:
$ \begin{aligned} & 5 x + 2 y \geq 30 \\ & 2 x + y \leq 15 \\ & x \leq y, x \geq 0, y \geq 0 \end{aligned} $
~~ 13. अधिकतम करें $Z = 100 x + 170 y$, को करें, उपेक्षा करें :
३ गुणा x + २ y ≤ ३६००, x + ४ y ≤ १८००, x ≥ ०, y ≥ ०
$
~~ १४. Z को अधिकतम करें: २०० x + १२० y के लिए इन शर्तों के आधार पर:
$ x+y ≤ ३००, ३ x+y ≤ ६००, y ≤ x+१००, x ≥ ०, y ≥ ० $
~~ १५. Z को अधिकतम करें: x+y के लिए विषयक
$ २ x+३ y ≤ १२०, ८ x+५ y ≤ ४००, x ≥ ०, y ≥ ० $
~~ १६. प्रकार A: ६, प्रकार B: ३; अधिकतम लाभ = रु. ४८०
~~ १७. २५७१.४३
~~ १८. १३८६००
~~ १९. प्रकार के १५० स्वेटर और अधिकतम लाभ = रु. ४८,०००
~~ २०. ५४ २/७ km।
~~ २१. ३ १०/११
~~ २२. मॉडल X: २५, मॉडल Y: ३० और अधिकतम लाभ = रु. ४०,०००
~~ २३. टैबलेट X: १, टैबलेट Y: ६
~~ २४. फैक्टरी I: ८० दिन, फैक्टरी II: ६० दिन
~~ २५. अधिकतम: १२, न्यूनतम मौजूद नहीं है
~~ २६. B
~~ २७. B
~~ २८. A
~~ २९. D
~~ ३०. C
~~ ३१. D
~~ ३२. D
~~ ३३. A
~~ ३४. B
~~ ३५. रैखिक प्रतिबंध
~~ ३६. रैखिक
~~ ३७. असीमित
~~ ३८. अधिकतम
~~ ३९. सीमित
~~ ४०. प्रांशित
~~ ४१. व्युत्पन्न
~~ ४२. सही
~~ ४३. गलत
~~ ४४. गलत
~~ ४५. सही
BETA
