अध्याय 10

द्रव्यों की यांत्रिकी गुणधर्म

एमसीक्यू I

10.1 एक लंबी सिलेंडर द्रविष्ट तेल से भरा होता है। शून्य प्रारंभिक वेग के साथ एक गोल चट्टान ऊपर से छोड़ी जाती है। चित्र 10.1 में दिखाए गए प्लॉट से, समय $(t)$ के एक फलन के रूप में पेबल की वेग $(v)$ का प्रतिष्ठान करने वाला एक करें।

(a)

(b)

(c)

(d)

चित्र 10.1

10.2 निम्नलिखित आरेखों में से कौन एक स्ट्रीमलाइन प्रवाह का प्रतिष्ठान नहीं करता है?

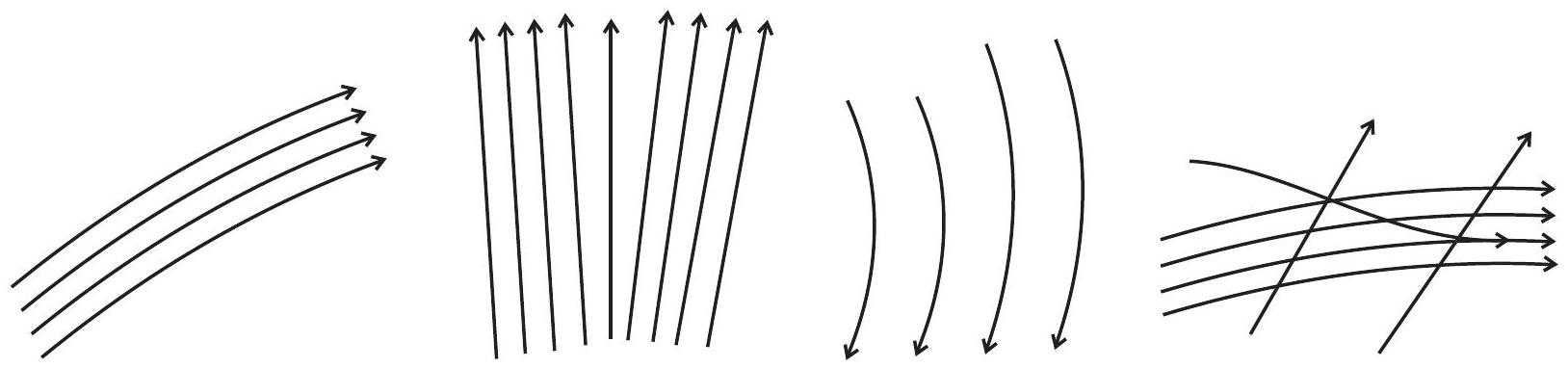
चित्र 10.2

10.3 एक स्ट्रीमलाइन के साथ

(a) एक द्रव तत्व की वेग निरंतर रहती है।

(b) दिए गए स्थान के सभी द्रव तत्वों की वेग निरंतर रहती है।

(c) एक विशिष्ट क्षण में सभी द्रव तत्वों की वेग निरंतर रहती है।

(d) एक द्रव तत्व की गति निरंतर रहती है।

10.4 एक आदर्श द्रव्य $2.5 \mathrm{~cm}$ और $3.75 \mathrm{~cm}$ व्यास के दो खंडों से बने एक नाली से बहता है। दो नालीयों में वेगों का अनुपात है

(a) $9: 4$

(b) $3: 2$

(c) $\sqrt{3}: \sqrt{2}$

(d) $\sqrt{2}: \sqrt{3}$

10.5 पानी-कांच के बीच संपर्क का कोण $0^{\circ}$ होता है, इथिलाल्कोहल-कांच के बीच संपर्क का कोण $0^{\circ}$ होता है, पारा-कांच के बीच संपर्क का कोण $140^{\circ}$ होता है और मिथाइलआयोडाइड-कांच के बीच संपर्क का कोण $30^{\circ}$ होता है। एक कांच की कैपिलरी को किसी छड़ी में डाला जाता है। यह देखा जाता है कि मेनिस्कस अभ्रधारी बनता है। छड़ी में द्रव है

(a) पानी

(b) इथिलाल्कोहल

(c) पारा

(d) मिथाइलआयोडाइड।

एमसीक्यू II

10.6 सतह तत्व के लिए

(a) इस पर जीवन में कोई प्रभावी बाधा नहीं होती है।

(b) इस पर नीचे की ओर कोई प्रभावी बाधा होती है।

(c) यहाँ तापीय ऊर्जा मोलेक्यूल के सीतल से कम होती है।

(d) यहाँ तापीय ऊर्जा मोलेक्यूल के सीतल से अधिक होती है।

10.7 दबाव एक स्केलर मात्री है क्योंकि

(a) यह बल की अनुपात को क्षेत्र के साथ और बल और क्षेत्र दोनों वेक्टर होते हैं।

(b) यह बल के मान को क्षेत्र के साथ अनुपातित करता है।

(c) यह बल के क्षेत्र के अंश के साथ अनुपातित करता है।

(d) यह क्षेत्र के चुने गए आयतन की आकार पर नहीं निर्भर करता है।

10.8 पानी में ऊपरिचय किये गए एक सिक्का संदूक में तैर रहा है, जैसा कि चित्र 10.3 में दिखाया गया है।

चित्र 10.3 के लिए, दूरी $l$ और $h$ दिखाई गई है। थोड़ी देर बाद सिक्का पानी में गिर जाता है। तब

(a) $l$ घटती है।

(b) $h$ घटती है।

की केंद्रीय मल्टीप्लिकेशन (c) $l$ बढ़ती है।

(d) $h$ बढ़ता है।

फ़िगर 10.3

10.9 तापमान बढ़ने से चपटता का विषारता कम होता है।

(a) गैसों की वृद्धि होती है।

(b) तरलों का विषारता बढ़ता है।

(c) गैसों की वृद्धि होती है।

(d) तरलों का विषारता कम होता है।

10.10 तरलों के लिए धारण विलयन सबसे अधिक संभावित है

(a) उच्च घनत्व।

(b) उच्च विषारता।

(c) कम घनत्व।

(d) कम विषारता।

एवीएस

10.11 क्या चपटता एक वेक्टर है?

10.12 क्या सतह तनाव एक वेक्टर है?

10.13 बर्फ़ हरी रंग की और भार में एक हिस्सा पानी में समय से उबर रहा है। बर्फ़ का घनत्व $\rho _{i}=$ $0.917 \mathrm{~g} \mathrm{~cm}^{-3}$ है।

10.14 एक बर्तन जल से भरा हुआ है और वजन पैन पर रखा है और माप को शून्य पर सेट किया जाता है। भार $M$ और घनत्व $\rho$ का एक ब्लॉक निस्सार्ण है जिसका स्प्रिंग संकेतक गति $k$ है। यह ब्लॉक विसर्जित है जल में जल में मारा। पैमाने का पढ़ना क्या है?

10.15 जल सतह पर तैरता हुआ एक क्यूबिकल ब्लॉक घनत्व का है $\rho$। इसकी ऊचाई $L$ में से हिस्सा $x$ पानी में डूबा हुआ है। बर्तन एक एलीवेटर में है जो एक सक्रियरि त्वरण $a$ के साथ ऊपर की और जा रहा है। घनिष्ठ हिस्सा क्या है?

एसए

10.16 पेड़ों में रस, जो मुख्य रूप से गर्मी में पानी से बना होता है, वृद्धि आणविकों के एक प्रणाली में बढ़ता है जिसकी अंदरूनी सतह $r=2.5 \times 10^{-5} \mathrm{~m}$ है। रस का सतह पर कशमकश $T=7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ है और संपर्क का कोण $0^\circ$ है। क्या कशमकश अकेले ही सभी पेड़ों के शीर्ष पर पानी की आपूर्ति के लिए जिम्मेदार है?

10.17 तैरते तेल की मुक्त सतह, आराम में, क्षैतिज है। यदि तेलकरी तेजी से आरंभ करता है तो मुक्त सतह को एक कोण $\theta$ से टिला जाता है। यदि त्वरण $a \mathrm{~m} \mathrm{~s}^{-2}$ है, तो मुक्त सतह का ढाल क्या होगा?

10.18 $0.1 \mathrm{~cm}$ और $0.2 \mathrm{~cm}$ के अर्धचंद्रकार में से दो मरकर की टिलाई जाती है। किस विलम्बित उर्जा की मात्रा उत्पन्न होती है? मरकर का कशम्मकश $T=435.5 \times 10^{-3} \mathrm{~N} \mathrm{~m}^{-1}$ है।

10.19 यदि तरल सहसंघटित होता है तो ध्रुवक जल कि तापमान क्या होता है? एक संकर नोक का तापमान $R$ होता है, $N$ छोटे तिपक्त्रविधी तापमान $r$ होते हैं। गिनति में क्या गिरावट होगी?

10.20 जल का छद्मता और वाष्पभाप $20^{\circ} \mathrm{C}$ पर $7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ और $2.33 \times 10^{3} \mathrm{~Pa}$ है, क्रमशः। $20^{\circ} \mathrm{C}$ पर वाष्पीय होने के बिना सबसे छोटी गोलाकार जल की आयाम क्या होगी?

ला

10.21 (a) दबाव आत्मस्फेर में एक जैसा बदलता है। यदि वायु का घनत्व $\rho$ है, तो आंतरिक ऊचाई $\mathrm{d} h$ पर दबाव $\mathrm{d} p$ में क्या परिवर्तन होगा?

(b) दबाव $p$ को घनत्व के अनुपात मानते हुए, सतह पर होने वाले दबाव $p$ क्या होगा यदि पृथ्वी की सतह पर दबाव $p_{0}$ है?

(c) यदि $p_{0}=1.03 \times 10^{5} \mathrm{~न्यूटन/मी}^{2}, \rho_{0}=1.29 \mathrm{~किलोग्राम/मी}^{3}$ और $g=9.8 \mathrm{~मी/सेकंड}^{2}$ हो, तो भूमि की सतह पर दबाव का मान $(1 / 10)$ बार दबाव कितनी ऊँचाई पर खत्म होगा?

(d) यह हवा के मानपर्ण मॉडल छोटी दूरियों के लिए काम करता है। हवा के मानकीय मॉडल की सीमा उद्देश्य क्या है?

10.22 द्रव में सतह जो तनावशीलता दिखाने वाली होती है, यह द्रव के कणों के बीच आकर्षण की शक्ति के कारण होती है। तनावशीलता गर्मी में बढ़ने के साथ कम होती है और उबलने पर लपट जाती है। जानते हुए कि पानी के वाष्पीकरण के लिए छलन स्वाधीनता $L_{v}=540 \mathrm{~किलोकैलोमीटर/किलोग्राम}$, ऊष्मीय स्वाधीनता $\mathrm{J}=4.2 \mathrm{~जूल/कैलोरी}$, पानी का घनत्व $\rho_{\mathrm{w}}=10^{3} \mathrm{~किलोग्राम/मीली मीटर}$, अवोगैड्रो क्रमांक $N_{\mathrm{A}}=6.0 \times 10^{26} \mathrm{~किलोमोल/मोल}^{-1}$ और पानी का आण्विक भार $M_{\mathrm{A}}=18 \mathrm{~किलोग्राम}$ है $1 \mathrm{~किलोमोल}$ के लिए।

(a) एक जल के कण के वाष्पीकरण के लिए ऊर्जा का अनुमान लगाएं।

(b) दिखाएं कि पानी के बीच कणों के बीच न्यूत्रों की दूरी $d=\left[\frac{M_{\mathrm{A}}}{N_{\mathrm{A}}} \times \frac{1}{\rho_{\mathrm{w}}}\right]^{1 / 3}$ होती है और इसका मान निर्धारित करें।

(c) $1 \mathrm{~ग्राम}$ वाष्प में पानी $1 \mathrm{~एटमॉस्फियर}$ पर $1601 \mathrm{~सेंटीमीटर}^{3}$ की जगह लेता है। ऊबलने के बिंदु पर न्यूत्रों की दूरी का अनुमान लगाएं, वाष्प की अवसाद की स्थिति में।

(d) स्वाधीनिकरण के दौरान एक कण $F$ बल, माना गया है, को एक न्यूत्री से $d$ से $d^{\prime}$ जाने के लिए पार करता है। $F$ का मान अनुमान लगाएं।

(e) $F / d$ की गणना करें, जो तनावशीलता का माप है।

10.23 एक गर्म हवा गुब्बारा एकरेखीयक $8 \mathrm{~मी}^2$. गुब्बारे के अंदर का हवा $60^{\circ} \mathrm{सेल्सियस}$ के तापमान पर है। जब बाहरी तापमान $20^{\circ} \mathrm{सेल्सियस}$ हो तो गुब्बारे का कितना भार उठा सकता है? (हवा को आदर्श गैस माना जाए, $R=8.314 \mathrm{~जूल/मोले} \mathrm{~केल्विन}^{-1}, 1 \mathrm{~एटमॉस्फियर}$.= $1.013 \times 10^{5} \mathrm{~पास्कल}$; परिदी में तनाव $5 \mathrm{~न्यूटन/मी}^{-1}$ है।)

समाधान 10

10.1 (c)

10.2 (d)

10.3 (b)

10.4 (a)

10.5 (c)

10.6 (a), (d)

10.7 (c), (d)

10.8 (a), (b)

10.9 (c), (d)

10.10 (b), (c)

10.11 नहीं।

10.12 नहीं।

10.13 इसे हमलावरों से पानी की घनत्व के समान लिया जा सकता है और तनावपूर्णता के माध्यम से माप ली जा सकती है।

10.14 $M g - (k x + \rho_{w} V g) = 0$ होता है जहां $\rho_{w}$ पानी का घनत्व है और $V$ ब्लॉक का आयतन है। पैन में पानी द्वारा दिए गए बल को पठनी पर प्रयोगित करने वाला रीडिंग है।

कंटेंट: $m_{\text {जहाज }}+m_{\text {पानी }}+\rho_{\mathrm{वी}} V g$ का ही संस्करण क्या है।

इसलिए ब्लॉक के बिना स्केल को शून्य पर समायोजित किया गया है, नया रीडिंग होता है $\rho_{\mathrm{वी}} V g$।

10.15 पानी की घनत्वा को $\rho_{w}$ मान लें।

तो $\rho a L^{3}+\rho L^{3} g=\rho_{\mathrm{वी}} x L^{3}(g+a)$

$\therefore x=\frac{\rho}{\rho_{\mathrm{वी}}}$

इस प्रकार, ब्लॉक डुबोया गया हिस्सा किसी भी त्वरण के बिना, चाहे वह गुरुत्वाकर्षण हो या लिफ्ट हो।

10.16 रस का जिसकी ऊचाई बढ़ेगी वह होगी

$h=\frac{2 T \cos 0^{\circ}}{\rho g r}=\frac{2\left(7.2 \times 10^{-2}\right)}{10^{3} \times 9.8 \times 2.5 \times 10^{-5}} \quad 0.6 \mathrm{~मीटर}$

यह सतह स्फीकटन के कारण जिस मात्रा में रस ऊभा सकता है, यह उच्चतम ऊचाई होती है। यहां तक कि बहुत से पेड़ों की ऊचाई बहुत अधिक होती है, कपिलरी कार्रवाई केवल सभी पेड़ों में पानी की उच्चता के लिए उचित नहीं है।

10.17 यदि टैंकर सक्रिय होता है पॉजिटिव $x$ दिशा में, तो पानी टैंकर के पीछे उमड़ जाएगा। मुक्त सतह ऐसी होगी कि किसी भी तरल पर्सल पर कोणांकीय बल शून्य होगा।

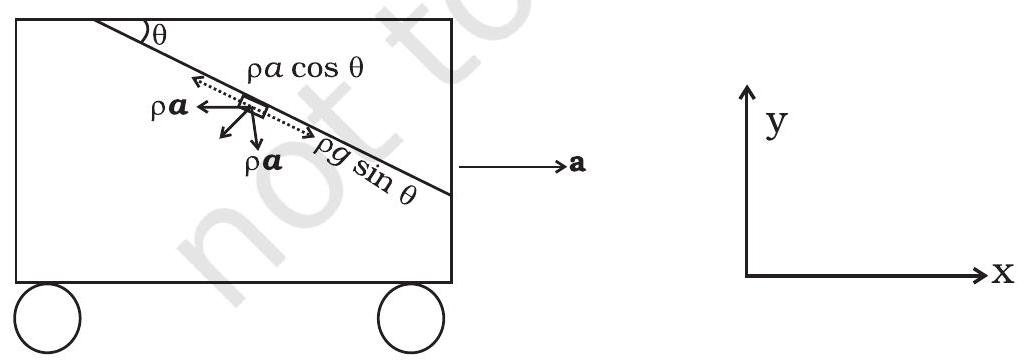
सतह पर एक पार्सल को मान एकाई वाला धरा के बने हुए भाग है। तरल पर बल निम्नलिखित होते हैं

$-\rho g \hat{\mathbf{y}}$ और $\quad-\rho a \hat{\mathbf{x}}$

तरल पर वजन का घटक सतह के साथ होता है $\rho g \sin \theta$

तरल पर त्वरण बल का घटक सतह के साथ होता है

$\rho a \cos \theta$

$\therefore \rho g \sin \theta=\rho a \cos \theta$

इसलिए, $\tan \theta=a / g$

10.18 $v_{1}$ और $v_{2}$ बूंदों की मात्रा हो और $v$ नतीजी बूंद की हो।

तो $v=v_{1}+v_{2}$

$\Rightarrow r^{3}=r_{1}^{3}+r_{2}^{3}=(0.001+0.008) \mathrm{cm}^{3}=0.009 \mathrm{~cm}^{3}$

$\therefore r \quad 0.21 \mathrm{~cm}$

$\therefore \Delta U=4 \pi T\left(r^{2}-\left(r_{1}^{2}+r_{2}^{2}\right)\right)$

$=4 \pi \times 435.5 \times 10^{-3}\left(0.21^{2}-0.05\right) \times 10^{-4} \mathrm{~J}$

$$ -32 \times 10^{-7} \mathrm{~J} $$

10.19 $R^{3}=N r^{3}$

$\Rightarrow r=\frac{R}{N^{1 / 3}}$

$\Delta U=4 \pi T\left(R^{2}-N r^{2}\right)$

अगर सभी इस ऊर्जा को तापमान कम करने के लिए खर्च करें तो तो बदलने कि नमूना शीतल होगी,

$$ \begin{aligned} & \Delta \theta=\frac{\Delta U}{m s}=\frac{4 \pi T\left(R^{2}-N r^{2}\right)}{\frac{4}{3} \pi R^{3} \rho s}, \text { यहां } \rho \text { घनत्वा है। } \ & \therefore \Delta \theta=\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{r^{2}}{R^{3}} N\right) \ & =\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{r^{2} R^{3}}{R^{3} r^{3}}\right)=\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{1}{r}\right) \end{aligned} $$

10.20 बूंद भाप से तब वाष्प दबाव पानी दबाव से अधिक होगा। परिमेंब्रेन दबाव (पानी)

$$ \begin{aligned} & p=\frac{2 T}{r}=2.33 \times 10^{3} \mathrm{~Pa} \ \end{aligned} $$

दिया गया सामग्री का हिन्दी संस्करण क्या होगा?

& \therefore r=\frac{2 T}{p}=\frac{2\left(7.28 \times 10^{-2}\right)}{2.33 \times 10^{3}}=6.25 \times 10^{-5} \mathrm{~m} \end{aligned} $$

10.21 (a) एक समतल एयर पार्सल की ऊचाई $d h$ और क्रॉस सेक्शन $A$ होती है। ऊपरी सतह और निचली सतह पर दबाव $p$ और $p+d p$ होता है। अगर पार्सल संतुलन में होता है, तो वजन द्वारा उत्पन्न संयुक्त उपरी बल को नीचे का वजन संतुलित करना चाहिए।

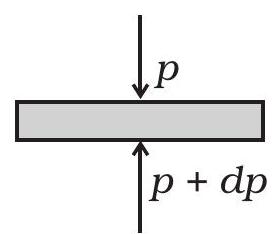
अर्थात् $(p+\mathrm{d} p) A-p A=-P g A d h$

$\Rightarrow \mathrm{d} p=-\rho g \mathrm{~d} h$

(b) पृथ्वी की सतह पर हवा का घनत्व $\rho_{0}$ हो, तब

$$ \begin{aligned} & \frac{p}{p_{o}}=\frac{\rho}{\rho_{o}} \ & \Rightarrow \rho=\frac{\rho_{o}}{p_{o}} p \end{aligned} $$

इसलिए $\mathrm{d} p=-\frac{\rho_{o} g}{p_{o}} p d h$

$\Rightarrow \frac{d p}{p}=-\frac{\rho_{o} g}{p_{o}} d h$

$\Rightarrow \int_{p_{o}}^{p} \frac{d p}{p}=-\frac{\rho_{o} g}{p_{o}} \int_{o}^{h} d h$

$\Rightarrow \ln \frac{p}{p_{o}}=-\frac{\rho_{o} g}{p_{o}} h$

$\Rightarrow p=p_{o} \exp \left(-\frac{\rho_{o} g}{p_{o}} h\right)$

(c) $\ln \frac{1}{10}=-\frac{\rho_{o} g}{p_{o}} h_{o}$

इसलिए, $h_{o}=-\frac{p_{o}}{\rho_{o} g} \ln \frac{1}{10}$

$=\frac{p_{o}}{\rho_{o} g} \times 2.303$

$=\frac{1.013 \times 10^{5}}{1.29 \times 9.8} \times 2.303=0.16 \times 10^{5} \mathrm{~m}=16 \times 10^{3} \mathrm{~m}$

(d) मान लें $p \propto \rho$ केवल उष्मीय मामले के लिए ही मान्य होता है जिसका केवल छोटे दूरी के लिए ही मान्य होता है।

10.22 (a) $1 \mathrm{~kg}$ जल के लिए $\mathrm{L}_{v} \mathrm{k}$ कैलोरी चाहिए

इसलिए $M_{\mathrm{A}} \mathrm{kg}$ जल के लिए $M_{\mathrm{A}} \mathrm{L}_{v} \mathrm{k}$ कैलोरी चाहिए

क्योंकि $M_{\mathrm{A}} \mathrm{kg}$ जल में $N_{\mathrm{A}}$ अणु होती हैं, इसलिए 1 अणु को उद्वासित करने के लिए आवश्यक ऊर्जा है

$$ \begin{aligned} u= & \frac{M_{A} L_{v}}{N_{A}} \mathrm{~J} \ = & \frac{18 \times \not 940 \times 4.2 \times 10^{3}}{\not 6 \times 10^{26}} \mathrm{~J} \ = & 90 \times 18 \times 4.2 \times 10^{-23} \mathrm{~J} \ & 6.8 \times 10^{-20} \mathrm{~J} \end{aligned} $$

(b) जल अणुओं को एक दूसरे से दूरी $d$ में होने का मान रखें।

$N_A$ अणुओं का जगह $\frac{M_A}{\rho_w}$ ली जाती है

इसलिए, एक अणु के आस-पास का आयतन $\frac{M_{A}}{N_{A} \rho_{w}} l$ होता है

इसलिए, एक अणु के आस-पास का आयतन $d^{3}=\left(\frac{M_A}{N_A \rho_w}\right)$

$$ \begin{aligned} \therefore d & =\left(\frac{M_{A}}{N_{A} \rho_{w}}\right)^{1 / 3}=\left(\frac{18}{6 \times 10^{26} \times 10^{3}}\right)^{1 / 3} \ & =\left(30 \times 10^{-30}\right)^{1 / 3} \mathrm{~m} \quad 3.1 \times 10^{-10} \mathrm{~m} \end{aligned} $$

(c) $1 \mathrm{~kg}$ वाष्प वस्त्र $1601 \times 10^{-3} \mathrm{~m}^{3}$ जगह का अधिकार करता है।

इसलिए, $18 \mathrm{~kg}$ वाष्प वस्त्र $18 \times 1601 \times 10^{-3} \mathrm{~m}^{3}$ जगह का अधिकार करता है

$\Rightarrow 6 \times 10^{26}$ अणुओं को $18 \times 1601 \times 10^{-3} \mathrm{~m}^{3}$ जगह का अधिकार करता है

उपस्थिति: $\therefore 1$ आण्विक इकाई $\frac{18 \times 1601 \times 10^{-3}}{6 \times 10^{26}} \mathrm{~मीटर}^{3}$ का दाखवते हैं।

यदि $d^{\prime}$ आंतरिक आण्विक दूरी है, तो

$$ \begin{aligned} & d^{3}=\left(3 \times 1601 \times 10^{-29}\right) \mathrm{मीटर}^{3} \ & \therefore \quad d^{\prime}=(30 \times 1601)^{1 / 3} \times 10^{-10} \mathrm{~मीटर} \ & =36.3 \times 10^{-10} \mathrm{~मीटर} \end{aligned} $$

(d) $F\left(d^{\prime}-d\right)=\mathrm{u} \Rightarrow F=\frac{u}{d^{\prime}-d}=\frac{6.8 \times 10^{-20}}{(36.3-3.1) \times 10^{-10}}=0.2048 \times 10^{-10} \mathrm{~न्यूटन}$

(e) $\quad F / d=\frac{0.2048 \times 10^{-10}}{3.1 \times 10^{-10}}=0.066 \mathrm{~न्यूटन} \mathrm{~मीटर}^{-1}=6.6 \times 10^{-2} \mathrm{~न्यूटन} \mathrm{~मीटर}^{-1}$

10.23 बैलूनमध्ये दाब आहे $P_{i}$ आणि बाहेरील दाब $P_{\mathrm{o}}$ आहे $P_{i}-P_{o}=\frac{2 \gamma}{r}$

एकात्मक गॅस म्हणून हवा दिलेलें मना

$P_{i} V=n_{i} R T_{i}$ ज्यात एकात्मक अंतःमोलाचा आणि $T_{i}$ अंतःमोलाची तापमान आहे आणि $P_{o} V=n_{o} R T_{o}$ ज्यात आणखी एकात्मक मोळाची आणि $T_{o}$ बाहेरील तापमान आहे।

$n_{i}=\frac{P_i V}{R T_{i}}=\frac{M_i}{M_A}$ ज्यात हव्याचे मोळे आणि $M_A$ हव्याचे मोळाचे मोलाचे वजन असे आणि $n_{\mathrm{o}}=\frac{P_{O} V}{R T_{O}}=\frac{M_{O}}{M_{A}}$ ज्यात बाहेरील हवा जे स्थानांतरित केले गेले आहे। जर $W$ ते लोड उच्चत होईल, तर $W+M_{i} g=M_{o} g$ $\Rightarrow W=M_{o} g-M_{i} g$

हवा $21 \% O_2$ आणि $79 \% N_2$ आहे

$\therefore$ हव्याचे मोळाचे वजन $M_{\mathrm{A}}=0.21 \times 32+0.79 \times 28=28.84 \mathrm{~ग्राम}$.

$\Rightarrow W=\frac{M_{A} V}{R}\left(\frac{P_{O}}{T_{o}}-\frac{P_{i}}{T_{i}}\right) g$

$=\frac{0.02884 \times \frac{4}{3} \pi \times 8^{3} \times 9.8}{8.314}\left(\frac{1.013 \times 10^{5}}{293}-\frac{1.013 \times 10^{5}}{333}-\frac{2 \times 5}{8 \times 313}\right) \mathrm{न्यूटन}$ $\frac{0.02884 \times \frac{4}{3} \pi \times 8^{3}}{8.314} \times 1.013 \times 10^{5}\left(\frac{1}{293}-\frac{1}{333}\right) \times 9.8 \mathrm{~यूज़ी}$

$=3044.2 \mathrm{~न्यूटन}$।