अध्याय 7

आवर्ती धारा

MCQ 1

~~ 7.1 यदि $50 Hz$ विद्युत धारा में प्रमाणित वातावरणी धारा $5 A$ है, तो उसकी मद्देनवंशीय विद्युत धारा का मान $1 / 300$ सेकंड बाद जब वह शून्य होती है, उसका मान है

(a) $5 \sqrt{2} A$

(b) $5 \sqrt{3 / 2} A$

(c) $5 / 6 A$

(d) $5 / \sqrt{2} A$

~~ 7.2 एक आवर्ती धारा उत्पादक के अंतर्नलीय प्रतिरोध $Rg$ और अंतर्नलीय प्रतिक्रिया $Xg$ होती है। इसे एक सक्रिय ढांचे को विद्युत शक्ति देने के लिए उपयोग किया जाता है, जिसमें एक प्रतिरोध $R g$ और प्रतिक्रिया $X_L$ होती है। उत्पादक से ढांचे तक से अधिकतम शक्ति आपूर्ति करने के लिए, $X_L$ का मान है

(a) शून्य।

(b) $X_g$।

(c) $-X_g$।

(d) $R_g$।

~~ 7.3 जब एक वोल्टेज मापन उपकरण को एसी मेन्स से जोड़ा जाता है, तो मीटर स्थिर आवेशी वोल्टेज $220 V$ दिखाता है। इसका अर्थ है

(a) इनपुट वोल्टेज एसी वोल्टेज नहीं हो सकती है, बल्कि एक डीसी वोल्टेज हो सकती है।

(b) अधिकतम इनपुट वोल्टेज $220 V$ है।

(c) मीटर $v$ नहीं पढ़ता है, बल्कि $\langle v^{2}\rangle$ पढ़ता है और $\sqrt{\langle v^{2}\rangle}$ पढ़ने के लिए कैलिब्रेट है।

(d) मीटर की संकेतक मेकैनिकल खराबी के कारण अटक जाता है।

~~ 7.4 एक जनसंख्या जेनरेटर के साथ एलसीआर श्रृंखलावार प्रकार के सर्किट में एलसीआर श्रृंखलावार संघ में reasonant आवृत्ति को कम करने के लिए

(a) जेनरेटर आवृत्ति को कम करनी चाहिए।

(b) पहली के समांतर को एक ऐलाक्ट्रोनिक टांक में जोड़ा जाना चाहिए।

(c) एलसीआर के इस्पातीय कोर को हटा देना चाहिए।

(d) कैपेसिटर में इलेक्ट्रानिक को कम करना चाहिए।

~~ 7.5 संचार के लिए उपयोग होने वाले ऐलसीआर सर्किट के बेहतर tuning के लिए निम्नलिखित में से कौन सा संयोजन चयन किया जाना चाहिए?

(a) $R=20 \Omega, L=1.5 H, C=35 \mu F$।

(b) $R=25 \Omega, L=2.5 H, C=45 \mu F$।

(c) $R=15 \Omega, L=3.5 H, C=30 \mu F$।

(d) $R=25 \Omega, L=1.5 H, C=45 \mu F$।

~~ 7.6 प्रतिक्रिया $1 \Omega$ की एक रेट्यूर की एक रेजिस्टर $2 \Omega$ के साथ एक $6 V(rms)$ वातावरणी विद्युत स्रोत के टर्मिनलों से संबंधित है। सर्किट में खप्पा पर्यवेक्षित किया जाता है

(a) $8 W$।

(b) $12 W$।

(c) $14.4 W$।

(d) $18 W$।

~~ 7.7 एक स्टेप-डाउन ट्रांसफार की उत्पादन देशांत्रिति $24 V$ होती है जब यह एक 12 वॉट बल्ब के साथ जुड़ा होता है। शीर्ष समय धारा का मान है

(a) $1 / \sqrt{2} A$।

(b) $\sqrt{2} A$।

(c) $2 A$।

(d) $2 \sqrt{2} A$।

MCQ II

~~ 7.8 जब एक एसी सर्किट की आवृत्ति बढ़ती है, तो विद्युत धारा सबसे पहले बढ़ती है और फिर घटती है। सर्किट किरणों का कौन सा संयोजन सबसे बहुत संभावित है?

(a) इंडक्टर और कैपेसिटर।

(b) रेजिस्टर और इंडक्टर।

(c) रेजिस्टर और कैपेसिटर।

(d) रेजिस्टर, इंडक्टर और कैपेसिटर।

~~ 7.9 एक सरियदारी में संचारी विद्युत धारा संज्ञानात्मक अवधि में बढ़ती हुई है। निम्नलिखित में से कौन से तत्व संचारी को सम्पन्न करने के लिए संभावित हैं?

(a) केवल रेजिस्टर।

(b) रेजिस्टर और इंडक्टर।

(c) रेजिस्टर और कैपेसिटर।

(d) केवल कैपेसिटर।

~~ 7.10 बड़ी दूरियों पर उच्च विद्युत वोल्टेज पर विद्युत ऊर्जा प्रेषित की जाती है। निम्नलिखित में से कौन सा कथन सही है?

(a) एक दिए गए शक्ति स्तर के लिए, एक निचली धारा होती है।

(b) निचली धारा से कम शक्ति की हानि होती है।

(सी) ट्रांसमिशन लाइनों को पतला बनाया जा सकता है।

(डी) प्राप्त करने वाले छूट ट्रांसफॉर्मर का उपयोग करके वोल्टेज को कम करना आसान है।

~~ 7.11 एक $L C R$ सर्किट के लिए, जो driving स्रोत से driven oscillator को पावर ट्रांसफर करता है, $P=I^{2} Z \cos \phi$ होता है।

(अ) यहाँ, पावर फैक्टर $\cos \phi \geq 0, P \geq 0$ होता है।

(ब) कुछ मामलों में, driving बल oscillator को कोई ऊर्जा नहीं दे सकता $(P=0)$।

(सी) driving बल oscillator से ऊर्जा स्याफन नहीं कर सकता $(P<0)$।

(डी) driving बल oscillator से ऊर्जा निकाल सकता है।

~~ 7.12 जब $220 V$ का एसी वोल्टेज को कैपेसिटर $C$ पर लागू किया जाता है

(अ) प्लेटों के बीच अधिकतम वोल्टेज $220 V$ होता है।

(ब) यह धारणा वोल्टेज के साथ समकोण में होती है।

(सी) प्लेटों पर आधारित धारा वोल्टेज के साथ समकोण में होती है।

(डी) कैपेसिटर को दिए जाने वाला पावर शून्य होता है।

~~ 7.13 यह वह रेखा है जो आपके घर को सड़क से पावर सप्लाई प्रदान करती है

(अ) शून्य औसत धारा।

(ब) $220 V$ औसत वोल्टेज।

(सी) वोल्टेज और धारा $90^{\circ}$ के फेज में होती है।

(डी) वोल्टेज और धारा $\phi$ में फेज में भिन्न हो सकती है जिसमें $|\phi|<\frac{\pi}{2}$ होता है।

~~ 7.14 यदि एक $L C$ सर्किट को हारमॉनिक तड़ित स्प्रिंग ब्लॉक सिस्टम के रूप में माना जाता है, तो $L C$ सर्किट का कौन सा ऊर्जा संभावित क्रियाशील अभिक्रिया के लिए किनेटिक ऊर्जा के समानांतर और कौन सा प्राच्य के लिए संभावित किनेटिक ऊर्जा के समानांतर होगा?

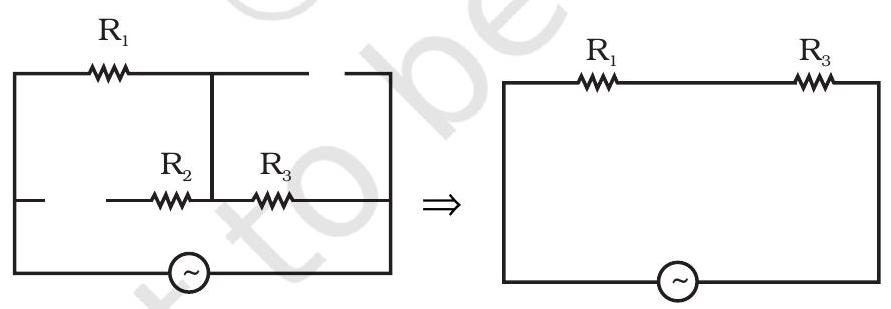
~~ 7.15 चित्र 7.1 में दिखाए गए सर्किट की प्रभावी समकक्षिकता सर्किट को बहुत ऊचे आवृत्तियों पर खींचें और प्रभावी आपेक्षिकता ढूंढें। 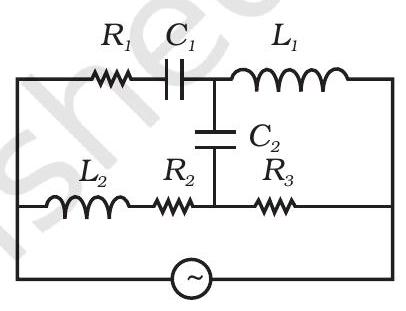चित्र 7.1

~~ 7.16 दी गई चित्र 7.2 में दिखाए गए सर्किट (अ) और (ब) की अध्ययन करें और निम्नलिखित प्रश्नों का उत्तर दें।

(अ)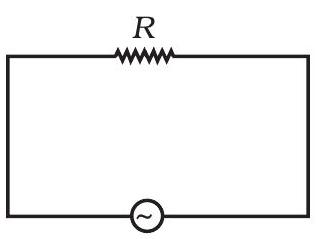

(ब) 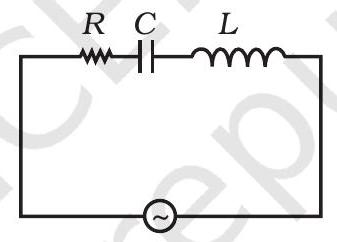चित्र 7.2

(अ) किस स्थितियों में दो सर्किटों में RMS धाराएँ समान होंगी?

(ब) क्या सर्किट (ब) में RMS धारा (अ) से अधिक हो सकती है?

~~ 7.17 क्या एक एसी स्रोत की क्षणिक बिजली उत्पादन कभी नकारात्मक हो सकती है? क्या औसत बिजली उत्पादन नकारात्मक हो सकती है?

~~ 7.18 श्रृंखला LCR सर्किट में, $I _{\max }$ vs $\omega$ का आदान-प्रदान चित्र 7.3 में दिखाया गया है। बैंडविड्थ ढूंढें और चित्र में चिह्नित करें।

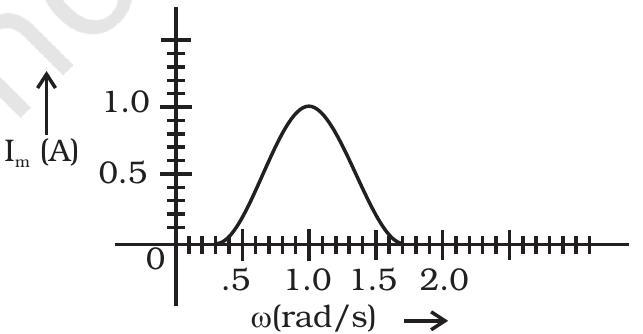चित्र 7.3

~~ 7.19 एक सर्किट में लगातार धारा द्वारा संक्रमित धारा चित्र चित्र 7.4 में दिखाया गया है। इस चित्र में rms धारा दिखाएं।

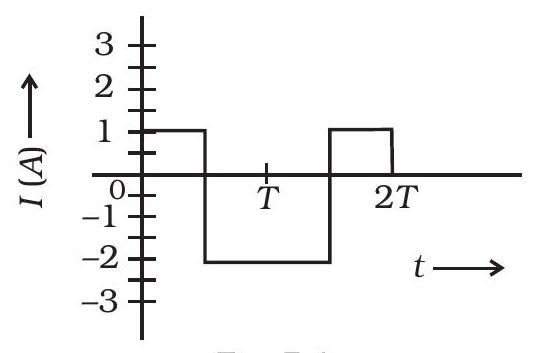चित्र 7.4

~~

7.20 प्रदान वोल्टेज आपूर्ति तंत्र में विद्युतधारा के साथ जो द्विदीपक के माध्यम से संचालित होता है, उसके संचालन फ्रीक्वेंसी को बहुत कम से बहुत उच्च मानों में धीरे-धीरे बढ़ाते समय, चरणांक फ़ेज का चिन्ह $ \phi $ कैसे बदलता है।

सारलकृत

~~ 7.21 एक उपकरण ’ $X$ ’ एक वैद्युतिन स्रोत से जुड़ा होता है। एक पूर्ण चक्र में वोल्टेज, धारा और विद्युत विन्यास का परिवर्तन चित्र 7.5 में दिखाया गया है।

(a) कौन सी कर्व पूरे चक्र पर विद्युत खपत दिखाती है?

(b) एक चक्र में औसत विद्युत खपत क्या है?

(c) उपकरण ’ $X$ ’ की पहचान करें।

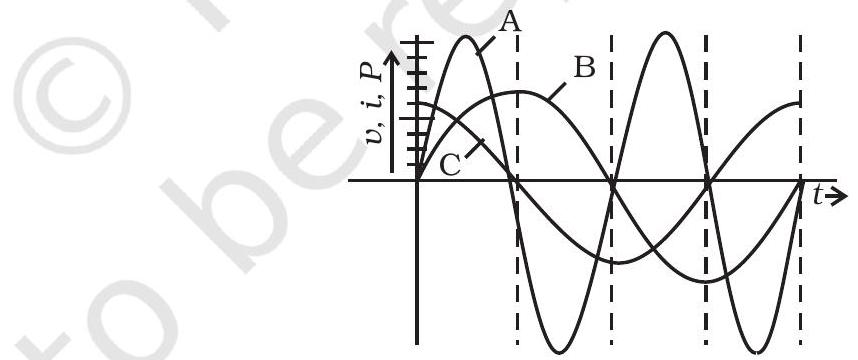चित्र 7.5

~~ 7.22 विद्युत धारा और सीधी धारा दोनों अम्पेर माप में की जाती है। लेकिन एक विद्युत धारा के लिए अम्पेर को कैसे परिभाषित किया जाता है?

~~ 7.23 0.01 हेंरी स्वेच्छ और $1 ओह्म$ विपथन को 200 वोल्ट, $50 Hz$ विद्युतापूर्ति से जोड़ा जाता है। परिधि का विपथन और अधिकतम वैद्युतापूर्ति और विद्युत धारा के बीच समय केन्द्रित करें।

~~ 7.24 एक प्राथमिक सेकंडरी के साथ जुड़े हुए एक $60 W$ भार के $0.54 A$ विद्युत धारा द्वारा विद्युत के प्राथमिक में कितनी धारा होती है? यहाँ बताएं कि कौन सा प्रकार का ट्रांसफार्मर इस्तेमाल किया जा रहा है।

~~ 7.25 स्वचालित विद्युत पर एक कैपेसिटर द्वारा प्रदान की जाने वाली प्रतिक्रिया क्योंकर तारंग में वृद्धि के साथ कम होती है, इसे समझाएं।

~~ 7.26 विद्युतापूर्ति के तरंगयुक्त वोल्टेज की बढ़ती आवृत्ति के साथ विद्युताप्रदान करने वाले इंडक्टर द्वारा प्रदान की जाने वाली प्रतिक्रिया क्यों बढ़ती है, इसे समझाएं।

संपर्क

~~ 7.27 एक विद्युतीय उपकरण वैकल्पिक्क धारा में मुख्यमंत्री के मुकाबले $223 V$ (rms) $=\sqrt{50,000} V$ वोल्टेज से $2 kW$ बिजली खींचता है। (रोह बांधता है) बिजली के संबंध में चर ज द्वारा प्रदत्त कॉसाइन गुणा पाया जाता है। (i) $R$, (ii) $X_C-X_L$, और (iii) $I_M$ पता करें। दूसरा उपकरण $R, X_C$ और $X_L$ के लिए दोहरा मान रखता है। उत्पन्न होने वाले समाधान पर कैसा प्रभाव पड़ता है?

~~ 7.28 $1MW$ ऊर्जा एक शहर $10 km$ की दूरी पर स्थित एक ऊर्जा स्थान से चलाई जानी चाहिए। इस उद्देश्य के लिए प्रयोग एक दोहरी स्थान तारों ($Cu$) का उपयोग करता है, जिनका त्रिज्या $0.5 cm$ है। यदि

(i) ऊर्जा $220 V$ पर चलाई जाए। इस तकनीक को करने की व्यवस्था के बारे में टिप्पणी करें।

(ii) एक सर्वर के उपयोग से वोल्टेज को $11000 V$ तक बढ़ाया जाता है, इसके बाद वोल्टेज को $220 V$ पर लाने के लिए एक सर्किट ट्रांसफार्मर का उपयोग किया जाता है।

$ (\rho _{C u}=1.7 \times 10^{-8} \text{ एसआई पद }) $

~~ 7.29 चित्र 7.6 में दिखाए गए $L C R$ सर्किट के लिए वाल्मीकि धारा $i$ और $i$ का चरण खोंजें। प्रदत्त सर्किट के लिए $Z$ माध्यम कोष पता करें। 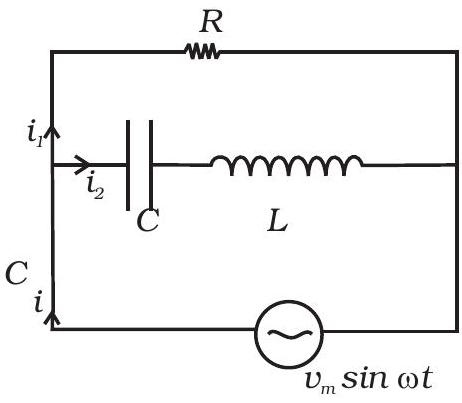चित्र 7.6

~~ 7.30 एक ऊर्जा संरक्षण की कथनात्मक रूप में बदलें जहां तकनीकी हो सके, संगणकीय रूप से व्याख्यात करें।

(iv) साइकिल के अवधि में समीकरण को एकीकृत करें और पाएं कि $v$ और i के बीच चरण विभाजन तेज़ होना चाहिए।

~~ 7.31 आदान-प्रदान संरचना में प्रदर्शित एल सी आर सर्किट में, ac ड्राइविंग वोल्टेज $v = v_m \sin \omega t$ होती है।

(i) $q(t)$ के लिए गति का समीकरण लिखें।

(ii) $t=t_0$ पर, वोल्टेज स्रोत बंद हो जाता है और $R$ को छोटा कर दिया जाता है। अब लिखें कि $L$ और $C$ में कितनी ऊर्जा संग्रहित होती है।

(iii) चार्जों के बाद की गति का वर्णन करें।

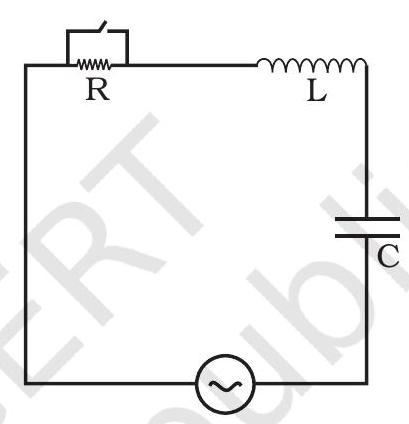चित्र 7.7

अध्याय 7

~~ 7.1 (बी)

~~ 7.2 (सी)

~~ 7.3 (सी)

~~ 7.4 (बी)

~~ 7.5 (सी)

~~ 7.6 (सी)

~~ 7.7 (ए)

~~ 7.8 (ए), (डी)

~~ 7.9 (सी), (डी)

~~ 7.10 (ए), (बी), (डी)

~~ 7.11 (ए), (बी), (सी)

~~ 7.12 (सी), (डी)

~~ 7.13 (ए), (डी)

~~ 7.14 चुंबकीय ऊर्जा संगत गतिविधि है और विद्युतीय ऊर्जा का संगणकीय ऊर्जा के समान रूप में है।

~~ 7.15 उच्च आवृत्तियों पर, कैपैसिटर $\approx$ शॉर्ट सर्किट (कम प्रतिक्रिया) होता है और इंडक्टर $\approx$ खुला सर्किट (उच्च प्रतिक्रिया) होता है। इसलिए, सर्किट पर्याय $Z \approx R_1+R_3$ होता है जैसा कि चित्र में दिखाया गया है।

~~ 7.16 (ए) हाँ, यदि दो सर्किटों में rms वोल्टेज समान हो तो संयोजन में, $L C R$ में rms current वो रहेगा जो $R$ सर्किट में है।

(ड) नहीं, क्योंकि $R \leq Z$, इसलिए $I_a \geq I_b$।

~~ 7.17 हाँ, नहीं।

~~ 7.18 बैंडविड्थ उन आवृत्तियों के प्रतिस्पर्धा के माध्यम से मानों पर प्रतिस्थानित होती है जहां $I_m=\frac{1}{\sqrt{2}} I _{\max }$ $\approx 0.7 I _{\max }$ होता है।

चित्र में दिखाया गया है।

$\Delta \omega=1.2-0.8=0.4 rad / s$

~~ 7.19 $I _{\text{rms }}=1.6 A$ (चित्र में अटूट रेखा द्वारा दिखाया गया है)

~~ 7.20 नकारात्मक से शून्य से सकारात्मक; संवेदनशील आवृत्ति पर शून्य।

~~ 7.21 (अ) ए

(ब) शून्य

(सी) $L$ या $C$ या $L C$

~~ 7.22 एसी विद्युत धारा स्रोत आवृत्ति और आकर्षक बल धातुमय परिवर्तन करती है और इसलिए स्रोत के दिशा के बारे में औसत कर्षण शून्य होगा। इस प्रकार, एसी एम्पीयर को केवल ऐसी गुणवत्ता के माध्यम से परिभाषित किया जाना चाहिए जो धारा की दिशा के निर्भर न हो। जूल का गर्मी प्रभाव ऐसी गुणवत्ता है और इसलिए एसी की rms मूल्य को परिभाषित करने के लिए उपयोग किया जाता है।

~~ 7.23 $ X_L=\omega L=2 \pi f L$

$=3.14 \Omega$

$Z=\sqrt{R^{2}+L^{2}}$

$=\sqrt{(3.14)^{2}+(1)^{2}}=\sqrt{10.86}$

$\simeq 3.3 \Omega$

$\tan \phi=\frac{\omega L}{R}=3.14$

$\phi=\tan ^{-1}(3.14)$

$\simeq 72^{\circ}$

$\simeq \frac{72 \times \pi}{180} rad$।

तारचाप $\Delta t=\frac{\phi}{\omega}=\frac{72 \times \pi}{180 \times 2 \pi \times 50}=\frac{1}{250} s$

~~ 7.24 $P_L=60 W, I_L=0.54 A$

$V_L=\frac{60}{0.54}=110 V$

ट्रांसफार्मर स्टेप-डाउन है और उसके पास $\frac{1}{2}$ इनपुट वोल्टेज है। इसलिए

$i_p=\frac{1}{2} \times I_2=0.27 A।

7.25 एक कैपेसिटर उसके गैप के रिजिस्टेंस बढ़ने के कारण इसके माध्यम से सीधी धारा को बहने नहीं देता है क्योंकि यह अनंत होता है। जब कैपेसिटर प्लेटों पर एक प्रतिस्थित वोल्टेज लगाया जाता है, तो प्लेटों को एक प्रतिस्थापित और डिसचार्ज किया जाता है। कैपेसिटर के माध्यम से धारा इस बदलते वोल्टेज (या आव्रती) के परिणामस्वरूप होती है। इस प्रकार, यदि वोल्टेज तेजी से बदल रहा है, अर्थात् सप्लाई की आवृत्ति अधिक है, तो कैपेसिटर में इसे अधिक धारा से बदल दिया जाएगा। इससे प्रमाणित होता है कि एक कैपेसिटर के द्वारा प्रदत्त यांत्रिक विलोमनमकता, आवृत्ति बढ़ने के साथ कम होती है; इस प्रकार इसे $1 / \omega C$ द्वारा दिया जाता है।

Exemplar Problems-Physics

7.26 एक इंडक्टर उसके माध्यम से धारा को बहने से रोकता है, जबकि विवरणा के अनुसार यह Lenz का नियम के अनुसार एक पिछला electromotive बनाता है। उत्पन्न वोल्टेज का आपेक्षित धारा मान को बनाए रखने के लिए उसकी पॉलैरिटी होती है। अगर धारा कम हो रहा है, तो उत्पन्न emf का धारा को बढ़ाने के लिए उसकी पॉलैरिटी होगी और उम्र-वृद्धि के उलट। क्योंकि उत्पन्न emf अनुपातित होता है धारा के परिवर्तन की दर से, इसलिए यदि धारा के परिवर्तन की दर अधिक है, तो यह धारा को अधिक विलोमनमकता प्रदान करेगा, अर्थात् यदि आपूर्ति की आवृत्ति अधिक है। इंद्रधनुषी के उलट। इंद्रि उल्ट। उत्पन्न इंद्रि ने ठ택ंक्ति में बढ़ी विलोमनमकता प्रदान की होगी, यह इस आवृत्ति के द्वारा दिया जाता है $\omega L$ के द्वारा।

7.27 Power $P=\frac{V^{2}}{Z} \Rightarrow \frac{50,000}{2000}=25=Z$

$Z^{2}=R^{2}+(X_C-X_L)^{2}=625$

$\tan \phi=\frac{X_C-X_L}{R}=-\frac{3}{4}$

$625=R^{2}+(-\frac{3}{4} R)^{2}=\frac{25}{16}$

$R^{2}=400 \Rightarrow R=20 \Omega$

$X_C-X_L=-15 \Omega$

$I=\frac{V}{Z}=\frac{223}{25} \simeq 9 A$.

$I_M=\sqrt{2} \times 9=12.6 A$.

अगर $R, X_C, X_L$ सब को दोगुना किया जाता है, तो $\tan \phi$ नहीं बदलता।

$Z$ दोगुना होता है, धारा आधी हो जाती है।

वस्तुत: ग्राह्य बिजली की आधी हो जाती है।

7.28 (i) $Cu$ तारों की रिस्टेंस, $R$

$=\rho \frac{l}{A}=\frac{1.7 \times 10^{-8} \times 20000}{\pi \times(\frac{1}{2})^{2} \times 10^{-4}}=4 \Omega$

$220 V$ पर $I: V I=10^{6} W ; I=\frac{10^{6}}{220}=0.45 \times 10^{4} A$

विद्धि नुकसान

$ \begin{aligned} & =4 \times(0.45)^{2} \times 10^{8} W \\ & >10^{6} W \end{aligned} $

यह विधि प्रेषण के लिए प्रयोग नहीं की जा सकती है

(ii) $V^{\prime} I^{\prime}=10^{6} W=11000 I^{\prime}$

$I^{\prime}=\frac{1}{1.1} \times 10^{2}$

$R I^{\prime 2}=\frac{1}{1.21} \times 4 \times 10^{4}=3.3 \times 10^{4} W$

नुकसान की शक्ति का अंश $=\frac{3.3 \times 10^{4}}{10^{6}}=3.3 %$

7.29

$R i_1=v_m \sin \omega t i_1=\frac{v_m \sin \omega t}{R}$

$\frac{q_2}{C}+L \frac{d q_2^{2}}{d t^{2}}=v_m \sin \omega t$

चेतना करें $q_2=q_m \sin (\omega t+\phi)$

$q_m(\frac{q_m}{C}-L \omega^{2}) \sin (\omega t+\phi)=v_m \sin \omega t$

$q_m=\frac{v_m}{\frac{1}{C}-L \omega^{2}}, \phi=0 ; \frac{1}{C}-\omega^{2} L>0$

$v_R=\frac{v_m}{L w^{2}-\frac{1}{C}}, \phi=\pi L \omega^{2}-\frac{1}{C}>0$

$i_2=\frac{d q_2}{d t}=\omega q_m \cos (\omega t+\phi)$

$i_1$ और $i_2$ आपस में फेज में हैं। चेतना करें $\frac{1}{C}-\omega^{2} L>0$

$i_1+i_2=\frac{v_m \sin \omega t}{R}+\frac{v_m}{L \omega-\frac{1}{c \omega}} \cos \omega t$

दिया गया सामग्री का हिंदी संस्करण क्या होगा: Now $A \sin \omega t+B \cos \omega t=C \sin (\omega t+\phi)$

$C \cos \phi=A, C \sin \phi=B ; C=\sqrt{A^{2}+B^{2}}$

इसलिए, $i_1+i_2=[\frac{v_m{ }^{2}}{R^{2}}+\frac{v_m{ }^{2}}{[\omega l-1 / \omega C]^{2}}]^{\frac{1}{2}} \sin (\omega t+\phi)$

$\phi=\tan ^{-1} \frac{R}{X_L-X_C}$

$\frac{1}{Z}={\frac{1}{R^{2}}+\frac{1}{(L \omega-1 / \omega C)^{2}}}^{1 / 2}$

~~ 7.30 $L i \frac{d i}{d t}+R i^{2}+\frac{q i}{c}=v i ; L i \frac{d i}{d t}=\frac{d}{d t}(\frac{1}{2} L i^{2})=$ rate of change of energy stored in an inductor.

$R i^{2}=$ joule heating loss

$\frac{q}{C} i=\frac{d}{d t}(\frac{q^{2}}{2 C})=$ rate of change of energy stored in the capacitor.

$v i=$ rate at which driving force pours in energy. It goes into (i) ohmic loss and (ii) increase of stored energy.

$\int_0^{T} d t \frac{d}{d t}(\frac{1}{2} i^{2}+\frac{q^{2}}{C})+\int_0^{T} R i^{2} d t=\int_0^{T} v i d t$ $0+(+v e)=\int_0^{T} v i d t$

$\int_0^{T}$ vidt $>0$ if phase difference, a constant is acute.

~~ 7.31 (i) $L \frac{d^{2} q}{d t^{2}}+R \frac{d q}{d t}+\frac{q}{C}=v_m \sin \omega t$

Let $q=q_m \sin (\omega t+\phi)=-q_m \cos (\omega t+\phi)$

$i=i_m \sin (\omega t+\phi)=q_m \omega \sin (w t+\phi)$

$i_m=\frac{v_m}{Z}=\frac{v_m}{\sqrt{R^{2}+(X_C-X_L)^{2}}} ; \phi=\tan ^{-1}(\frac{X_C-X_L}{R})$

(ii) $U_L=\frac{1}{2} L i^{2}=\frac{1}{2} L[\frac{v_m}{\sqrt{.R^{2}+X_C-X_L)^{2}}}]^{2} \sin ^{2}(\omega t_0+\phi)$

$U_C=\frac{1}{2} \frac{q^{2}}{C}=\frac{1}{2 C}[\frac{v_m}{\sqrt{R^{2}+(X_C-X_L)^{2}}}]^{2} \frac{1}{\omega^{2}} \cos ^{2}(\omega t_0+\phi)$

(iii) Left to itself, it is an $L C$ oscillator. The capacitor will go on discharging and all energy will go to $L$ and back and forth.