अध्याय १५

संचार प्रणालियाँ

एमसीक्यू आई

~~ १५.१ स्थान सतह तारंग (A), आकाशीय तारंग (B) और स्वच्छंद तारंग (C) की तीन तारंगों की आवृत्तियां $१६०० \ किलोहर्ट्ज, \ ५ \ मेगाहर्ट्ज$ और $६० \ मेगाहर्ट्ज$ हैं, स्थान से दूसरे स्थान पर प्रेषित की जाती हैं। निम्नलिखित में से सबसे उपयुक्त संचार प्रणाली कौन सी है:

(a) A को अंतरिक्ष तारंग द्वारा और $B$ और $C$ को आकाशीय तारंग द्वारा प्रेषित किया जाता है।

(b) A को भूतल तारंग द्वारा, $B$ को आकाशीय तारंग द्वारा और $C$ को अंतरिक्ष तारंग द्वारा प्रेषित किया जाता है।

(c) $B$ और $C$ को भूतल तारंग द्वारा प्रेषित किया जाता है जबकि $A$ को आकाशीय तारंग द्वारा प्रेषित किया जाता है।

(d) B को भूतल तारंग द्वारा प्रेषित किया जाता है जबकि $A$ और $C$ को अंतरिक्ष तारंग द्वारा प्रेषित किया जाता है।

~~ १५.२ एक $५०० \ मीटर$ ऊँचाई वाली इमारत पर एक $१०० \ मीटर$ लंबी एंटीना स्थापित है। जिन तारंगों के लिए कम्प्लेक्स एक प्रसारण टावर बन सकता है जिनमें $\lambda$ होता है

(a) $\sim ४०० \ मीटर$।

(b) $\sim २५ \ मीटर$।

(c) $\sim १५० \ मीटर$।

(d) $\sim २४०० \ मीटर$।

~~ १५.३ एक $१ \ किलोवाट$ संकेत को $-२ \ डीबी$ प्रति $किलोमीटर$ की गति से अवशोषण प्रदान करने वाले संचार चैनल का उपयोग किया जाता है। यदि संचार चैनल की कुल लंबाई $५ \ किलोमीटर$ होती है, तो प्राप्ति हुए संकेत की शक्ति होगी [अधिकार में $डीबी=१० \ लॉग (\frac{पी०}{पी})$ ]

(a) $९०० \ वाट्स$।

(b) $१०० \ वाट्स$।

(c) $९९० \ वाट्स$।

(d) $१०१० \ वाट्स$।

~~ १५.४ एक बोली संकेत $३ \ किलोहर्ट्ज$ का उपयोग करता है जो एक कैरियर संकेत $१ \ मेगाहर्ट्ज$ को मोडुलेशन करने के लिए उपयोग करता है। साइड बैंड की आवृत्तियां होंगी

(a) $१.००३ \ मेगाहर्ट्ज$ और $०.९९७ \ मेगाहर्ट्ज$।

(b) $३००१ \ किलोहर्ट्ज$ और $२९९७ \ किलोहर्ट्ज$।

(c) $१००३ \ किलोहर्ट्ज$ और $१००० \ किलोहर्ट्ज$।

(d) $१ \ मेगाहर्ट्ज$ और $०.९९७ \ मेगाहर्ट्ज$।

~~ १५.५ एक संदेश संकेत में आवृत्ति $\omega_m$ एक कैरियर तारंग $\omega_c$ पर सुपरिमेशन होती है (ऐएम)। ऐएम तारंग की आवृत्ति होगी

(a) $\omega_m$।

(b) $\omega_c$।

(c) $\frac{\omega_c+\omega_m}{2}$।

(d) $\frac{\omega_c-\omega_m}{2}$।

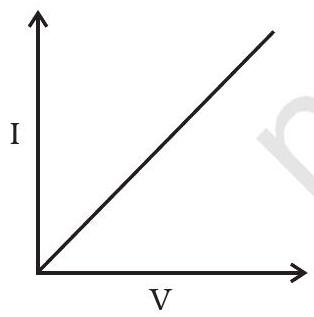
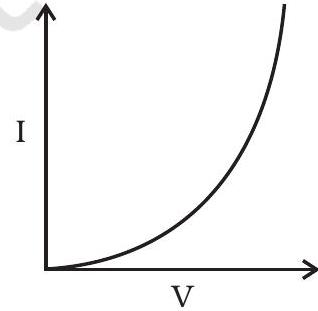
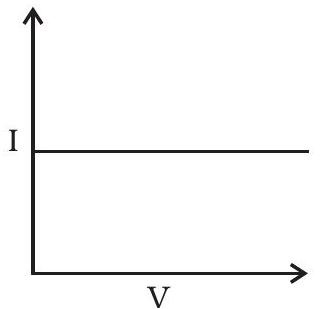
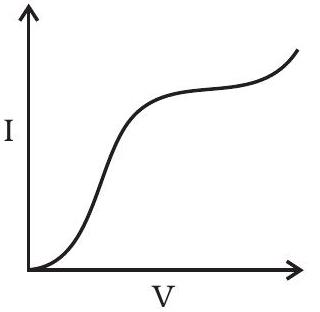
~~ १५.६ चार उपकरणों की $आई-वी$ विशेषताओं को चित्र १५.१ में दिखाया गया है

(i)

(ii)

(iii)

(iv) चित्र १५.१

मोडुलेशन के लिए उपयोग किए जा सकने वाले उपकरणों की पहचान करें:

(a) ‘i’ और ‘iii’।

(b) केवल ‘iii’।

(c) ‘ii’ और ‘iv’ के कुछ क्षेत्र।

(d) सभी उपकरण प्रयोग किए जा सकते हैं।

~~ १५.७ एक पुरुषी आवाज मोडुलेशन-प्रेषण के बाद स्वीकार करने वाले के लिए एक महिला के जैसा आवाज सुनाई देता है। समस्या कारण है

(a) मोडुलेशन अनुपात के खराब चयन (चयनित $०<m<१$)

(b) एंप्लीफायर्स के लिए गरीब बैंडविड्थ चयन।

(c) कैरियर तारंग के खराब चयन

(d) प्रेषण में ऊर्जा का हानि।

~~ १५.८ एक मूल संचार प्रणाली में शामिल होता है

(A) प्रेषक।

(B) सूचना स्रोत।

(C) सूचना का उपयोग करने वाला उपभोक्ता।

(D) चैनल।

(E) प्राप्त करने वाला।

कृपया एक मूल्यांकन प्रणाली में जहां ये व्यवस्थित होते हैं, इनके सही क्रम का चयन करें:

(a) ABCDE.

(b) BADEC.

(c) BDACE.

(d) BEADC.

~~ 15.9 तीव्रता संचालित तरंग के लिए गणितीय व्यक्ति किया जा सकता है:

(a) $A_c \sin [{\omega_c+k_1 v_m(t)} t+\phi]$.

(b) $A_c \sin {\omega_c t+\phi+k_2 v_m(t)}$.

(c) ${A_c+k_2 v_m(t)} \sin (\omega_c t+\phi)$.

(d) $A_c v_m(t) \sin (\omega_c t+\phi)$.

MCQ II

~~ 15.10 एक ध्वनि संकेत $15 kHz$ आवृत्ति को बिना परिवर्तन किए दूर संचारित नहीं किया जा सकता है क्योंकि

(a) आवश्यक एंटीना का आकार कम से कम $5 km$ होगा, जो अनुकूल नहीं है। (b) आकाश तरंगों के माध्यम से ध्वनि संकेत संचारित नहीं किया जा सकता।

(c) आवश्यक एंटीना का आकार कम से कम $20 km$ होगा, जो अनुकूल नहीं है।

(d) अगर एंटीना का आकार $5 km$ से कम हो तो प्रभावी ताकत की त्रांसमीट की जाती है, अगर अंतेना का आकार $5 km$ से कम हो।

~~ 15.11 $3 kHz$ आवृत्ति के ध्वनि साइन तरंगों का उपयोग $1.5 MHz$ के कैरियर सिग्नल को अंदर बाहर करने के लिए किया जाता है। निम्न में से कौन से बयान सही हैं?

(a) साइड बैंड आवृत्तियाँ $1506 kHz$ और $1494 kHz$ हैं।

(b) ध्वनि संचार के लिए आवश्यक बैंडविड्थ $6 kHz$ है।

(c) ध्वनि संचार के लिए आवश्यक बैंडविड्थ $3 MHz$ है।

(d) साइड बैंड आवृत्तियाँ $1503 kHz$ और $1497 kHz$ हैं।

~~ 15.12 टीवी प्रसारण टावर की ऊंचाई $240 m$ है। इस टावर से प्रसारित सिग्नल LOS संचार द्वारा दूरी पर प्राप्त होंगे (भूमि के तत्वावधान से $6.4 \times 10^{6} m$ रेडियस, मान लें)

(a) $100 km$.

(b) $24 km$.

(c) $55 km$.

(d) $50 km$.

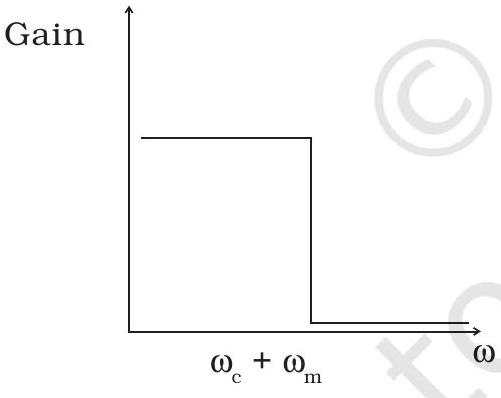
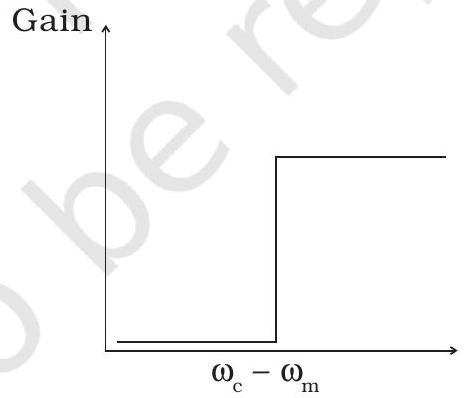
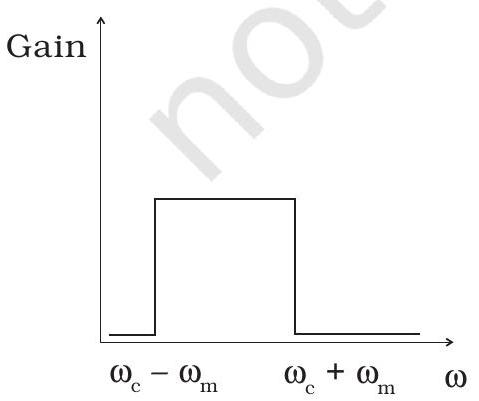
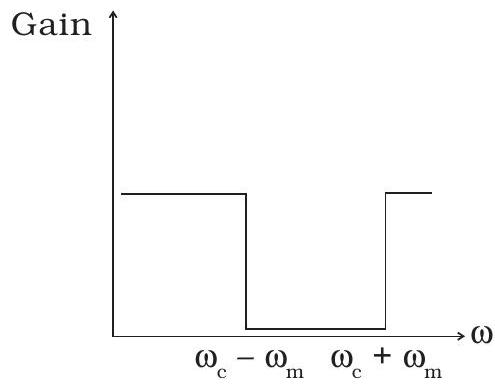
~~ 15.13 अम्पलीट्यूड मॉडुलेशन के लिए उपयोग होने वाले फ़िल्टर सर्किट के लिए आवृत्ति प्रतिक्रिया ग्राफ (चित्र. 15.2) होनी चाहिए

(i)

(ii)

(iii)

(iv) चित्र 15.2

(a) (i) के बाद (ii).

(b) (ii) के बाद (i).

(c) (iii).

(d) (iv).

~~ 15.14 अंदर बाहर करने में, मोड्यूलेशन संख्या $m$ को 1 से कम या बराबर रखा जाता है क्योंकि

(a) $m>1$, जो बाहरीत तरंग आवष्टिति एंटीना की संयोजन संख्या और संदेश आवृत्ति के बीच अवरोहिति से आवरोहिति में अवरोध पैदा करेगा।

(b) $m>1$, इससे दोनों तरफ़ी एंटीना के अंतर्ज्ञान के परिणामस्वरूप दोनों तरफ़ी आवृत्तियाँ टकराएगी।

(c) $m>1$, इससे ऑफसेटिंग संकेत तथा संदेश संकेत के बीच उत्पन्न होने वाले चरावण को बदल देगा।

(d) $m>1$ में संदेश संकेत की आंच क्षेत्रीय संकेतों की आंच से अधिक होगी, जिससे आवरोध पैदा होगा।

VSA

~~ 15.15 निम्नलिखित में से कौन सा एनालॉग संकेत प्रदान करेगा और कौन सा डिजिटल संकेत प्रदान करेगा?

(i) एक वायरेटिंग ट्यूनिंग फोर्क।

(ii) स्वर ध्वनित सितार स्ट्रिंग के कारण संगीतीय आवाज।

(iii) प्रकाश पल्स।

(iv) NAND गेट का आउटपुट।

~~ 15.16 क्या आकाशीय तारंगें $60 मेगाहर्ज$ फ्रिक्वेंसी के टीवी संकेतों के प्रसारण के लिए उपयुक्त हो सकती हैं?

~~ 15.17 एक दिशा में संचार के लिए दो तारंग A और B ($2 मेगाहर्ज$ और $3 मेगाहर्ज$ फ्रिक्वेंसी वाली) आकाशीय तारंगें उठाई जाती हैं। इनमे से कौन सी तारंग पूरी तृणमयी में टोटल इंटरनल रिफ्लेक्शन करने से पहले अधिक दूरी चल सकती है?

~~ 15.18 एक एएम तारंग का अधिकतम आम्लीयता $15 वोल्ट$ और न्यूनतम आम्लीयता $3 वोल्ट$ पाई जाती है। मॉड्युलेशन सूचक?

~~ 15.19 एक ट्यून्ड एंप्लिफायर सर्किट का $L C$ उत्पादन $1 मेगाहर्ज$ की कैरियर तारंग उत्पन्न करने के लिए कितना होना चाहिए?

~~ 15.20 एक एएम संकेत क्यों एक एफएम संकेत की तुलना में प्रसारण के माध्यम से अधिक शोरी होने के योग्य है?

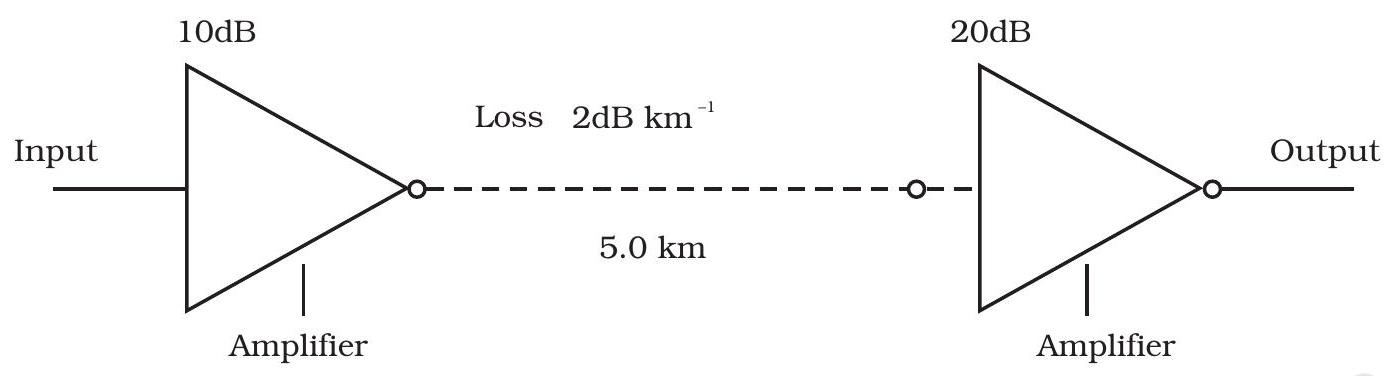
~~ 15.21 आईंटपुट शक्ति क्या होगी जब इनपुट संकेत $1.01 मिलीवॉट$ का होगा? (गेन $डीबी=10 \log _{10}$ $(P_o / P_i)$।

चित्र 15.3

~~ 15.22 एक टीवी प्रसारण टॉवर एंटीना $20 मीटर$ ऊंचाई पर है। यदि प्राप्ति एंटीना (i) भूमि स्तर पर हो, (ii) $25 मीटर$ ऊंचाई पर हो तो कितनी सेवा क्षेत्र को यह कवर कर सकती है? इतने क्षेत्र में क्षेत्र की वृद्धि का प्रतिशत गणना करें (ii) के मुकाबले (i) के संबंध में।

~~ 15.23 यदि संचार के लिए पृथ्वीरेखा प्रयोग करके स्थानीय मुद्रिका वाले संचार का प्रयोग किया जाता है (एंटीना आकार या टॉवर ऊचाई पर कोई प्रतिबंध नहीं है), तो न्यूनतम संख्या एंटीना कुछ हो सकती है? पृथ्वी के त्रिज्या के हिसाब से इन एंटीना की टॉवर ऊंचाई का आकलन करें।

~~ 15.24 एक निर्दिष्ट आयन संकेतों के उरावतार से आकाशीय तारंगों के लिए अधिकतम फ्रिक्वेंसी का माप $f _{\max }=9(N _{\max })^{1 / 2}$ साबित होता है, जहां $N _{\max }$ आयनस्फेर की उस परत की अधिकतम इलेक्ट्रॉन घनता है। एक निश्चित दिन पर देखा जाता है कि $5 मेगाहर्ज$ से अधिक फ्रिक्वेंसी के संकेत आयनस्फेर की $F_1$ परत से रिफ्लेक्शन करके प्राप्त नहीं होते हैं जबकि $8 मेगाहर्ज$ से अधिक फ्रिक्वेंसी के संकेत आयनस्फेर की $F_2$ परत से रिफ्लेक्शन करके प्राप्त नहीं होते हैं। उस दिन पर $F_1$ और $F_2$ परतों की अधिकतम इलेक्ट्रॉन घनताओं का आकलन करें।

~~ 15.25 एक एएम मॉड्युलेटेड संकेत को रेडिएट करने पर, कुल रेडिएटेड शक्ति $\omega_c, \omega_c-\omega_m & \omega_c+\omega_m$ द्वारा परिवहन कीय ऊर्जा के कारण होती है। जानकारी पर ध्यान नहीं देते हुए रेडिएशन की लागत को न्यूनतम करने के तरीके सुझाएं।

LA

~~ 15.26 (i) दूरी $x$ के साथ आगे बढ़ने वाले एक प्रकाश पल्स की तीव्रता $I=I_0 e^{-\alpha x}$ के अनुसार धीमी होती है, जहां $I_0$ नापी $x=0$ पर तीव्रता है और $\alpha$ लघु होता है।

दिखाएं कि दूरी $(\frac{\ln 4}{\alpha})$ के बाद तीव्रता $75$ प्रतिशत कम होती है।

(ii) सिग्नल की दबावता को डेसिबल (डीबी) में व्यक्त किया जा सकता है जिसका संबंध नियम के अनुसार है $डीबी=10 \log_{10}(\frac{I}{I_o})$ कैसे ऑप्टिकल फाइबर में $50 किमी$ की दूरी पर जहाँ तीव्रता $50$ प्रतिशतमा घटती है, वहाँ की तड़पन $डीबी/किमी$ में क्या होगी?

~~ 15.27 एक $50 एमएचज़ी$ आकाशीय तरंग $4.04 माइक्रोसेकंड$ लेती है ताकि वह प्राप्ति स्थल तक पहुंच सके उच्चतम से निम्नतम स्थलांतरण से, वह निर्धारण करें कि स्रोत और प्राप्त करने वाले की दूरी क्या है। यदि इन दोनों के बीच संचार लाइन दृष्टि (LOS) विधि से किया जाना होता है, तो प्राप्ति करने और भेजने वाले एंटीना के आकार और स्थान पर क्या होना चाहिए?

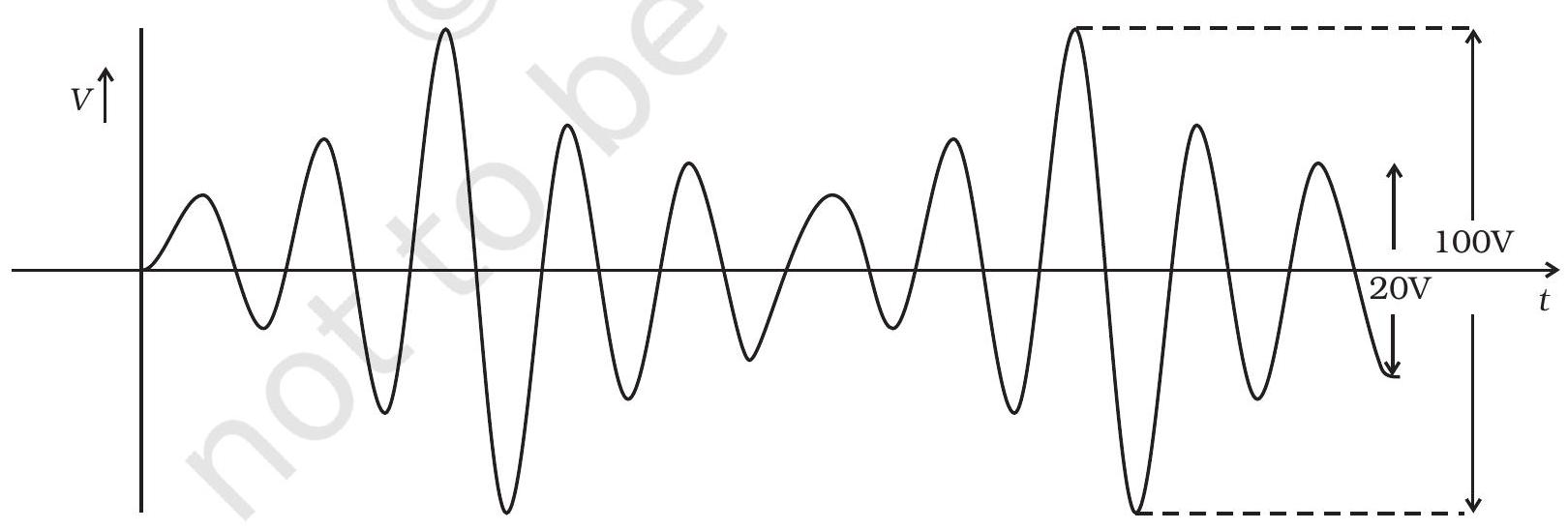
~~ 15.28 एक प्रतीमान धारित तरंग आरेख छवि 15.4 में दिखाई दी जाती है। हिग्स संप्रेषक का प्रतिशत मोडुलेशन (i), शीर्ष वाहक वोल्टेज (ii) और सूचना वोल्टेज की शीर्ष मान (iii) की गणना करें।

चित्र 15.4

~~ 15.29 (i) घटाव की प्लॉट ’ $\omega$ ’ के लिए खींचें जो एक घटावित तरंग है जिसका वाहक तरंग $(\omega_c)$ दो मोडुलेटेड संकेतों, $\omega_1$ और $\omega_2(\omega_2>\omega_1)$, को ले रहा है। [संकेत मित्रता के ईक 15.6 से निर्देश पेश करें: NCERT बारहवीं कक्षा के पाठ्यपुस्तक]

(ii) क्या प्लॉट $\omega_c$ के बारे में समरूप है? खासकर $\omega<\omega_c$ वाले क्षेत्र में प्लॉट के बारे में टिप्पणी करें।

(iii) अतिरिक्त और अधिक संकेतों को मोडुलेट करने की समस्याओं की पूर्वानुमान करें और उसके बारे में समाधान सुझाएं। प्रक्रिया में क्या कसौटी मोडुलेशन के एक अन्य लाभ को व्यापबंध के माध्यम से समझ सकते हैं?

~~ 15.30 एक ऑडियो संकेत को $20 एमएचज़ी$ के एक कैरियर तरंग द्वारा मोडुलेट किया गया है जिससे मोडुलेशन के लिए आवश्यक बैंडविड्थ $3 कि.हे.$ है। क्या इस तरंग को एक डायोड डिटेक्टर द्वारा जिसकी मानें इस प्रकार हैं $R=1 किलो ओम, C=0.01 माइक्रोफ़ाराड$ (i), $R=10 किलो ओम, C=0.01 माइक्रोफ़ाराड$ (ii), $R=10 किलो ओम, C=0.1 माइक्रोफ़ाराड$ (iii) द्वारा डिमॉडुलेट किया जा सकता है?

अध्याय 15

~~ 15.1 (बी)

~~ 15.2 (ए)

~~ 15.3 (ए)

~~ 15.4 (ए)

~~ 15.5 (बी)

~~ 15.6 (सी)

~~ 15.7 (बी)

~~ 15.8 (बी)

~~ 15.9 (सी)

~~ 15.10 (अ), (ब), (घ)

~~ 15.11 (ब), (घ)

~~ 15.12 (ब), (सी), (घ)

~~ 15.13 (अ), (ब), (सी)

~~ 15.14 (ब), (घ)

~~ 15.15 (ई) ऐनालॉग

(आई) ऐनालॉग

(iii) डिजिटल

(iv) डिजिटल

~~ 15.16 नहीं, $30 मेगाहर्ट्ज़$ से अधिक तरंगों को आयोनमंडल द्वारा परावर्तित नहीं किया जाएगा, लेकिन वे आयोनमंडल से पेनेट्रेट कर जाएंगे।

~~ 15.17 अभिफ्रेक्टिव सूचकांक चुटकीमार से बढ़ने के साथ बढ़ता है जिसका मतलब है कि अधिकतर तारंगिकता वाले तरंगों के लिए प्रतिघात का कोण कम होता है, अर्थाता मुड़ाव कम होता है। इसलिए, पूर्ण आंतरिक परावर्तन की स्थिति उससे बड़ी दूरी तय करने के बाद होती है (बात का कक्षा $3 मेगाहर्ट्ज़$ तरंग द्वारा की गई है)।

~~ 15.18 $A_c+A_m=15, A_c-A_m=3$

$\therefore 2 A_c=18,2 A_m=12$

$\therefore m=\frac{A_m}{A_c}=\frac{2}{3}$

~~ 15.19 $ \frac{1}{2 \pi \sqrt{L C}}=1 मेगाहर्ट्ज़$

$\sqrt{LC}=\frac{1}{2 \pi \times 10^{6}}$

~~

15.20 एएम में, कैरियर तलवार के स्थानिक वोल्टेज को माप करने वाला तरंग स्तर तरंगों के वोल्टेज द्वारा विभिन्न किया जाता है। प्रेषण में, शोर चिंताओं को भी जोड़ा जा सकता है और प्राप्तकर्ता को शोर को चरणीय संकेत का हिस्सा मानता है।

हालांकि, एफएम में, कैरियर का आवृत्ति विभिन्न होती है सतत थोड़े वोल्टेज के अनुसार। यह केवल मिश्रण / द्वीपक के स्तर में हो सकता है और संकेत चैनल में संकेत प्रेषित हो रहे समय नहीं। इसलिए, शोर एफएम संकेत पर प्रभाव नहीं डालता है।

~~ 15.21 प्रेषण मार्ग में हुए नुकसान

$=-2 , डीबी , किमी^{-1} \times 5 , किमी=-10 , डीबी$

कुल प्रभावक गुण $=10 , डीबी+20 , डीबी$

$\begin{aligned} &=30 , डीबी \end{aligned}$

संकेत की संपूर्ण प्राप्ति $=30 , डीबी-10 , डीबी$

$=20 , डीबी$

$\begin{aligned} &10 \log \left(\frac{{पी_o}}{{पी_i}}\right) \quad=12 , या , पी_o =पी_i \times 10^{2} \\ &=1.01 , मि.वॉट्स \times 100=101 , मि.वॉट्स . \end{aligned}$

~~ 15.22 (i) दायरा $=\sqrt{2 \times 6.4 \times 10^{6} \times 20}=16 , किमी$

क्षेत्र शामिल $=803.84 , किमी^{2}$

(ii) दायरा $=\sqrt{2 \times 6.4 \times 10^{6} \times 20}+\sqrt{2 \times 6.4 \times 10^{6} \times 25}$

$=(16+17.9) , किमी=33.9 , किमी$

क्षेत्र शामिल $=3608.52 , किमी^{2}$

$\therefore$ क्षेत्र में वृद्धि का प्रतिशत

$\begin{aligned} &=\frac{{(3608.52-803.84)}}{{803.84}} \times 100 \\ &=348.9 % \end{aligned}$

~~ 15.23 $d_m^{2}=2(R+h_T)^{2}$

$8 , R , h_T=2(R+h_T)^{2}$

$(इसलिए डी एम=2 \sqrt{2 , R , h_T})$

$4 , R , h_T=R^{2}+h_T^{2}+2 , R , h_T$

$(R-h_T)^{2}=0$

$R=h_T$

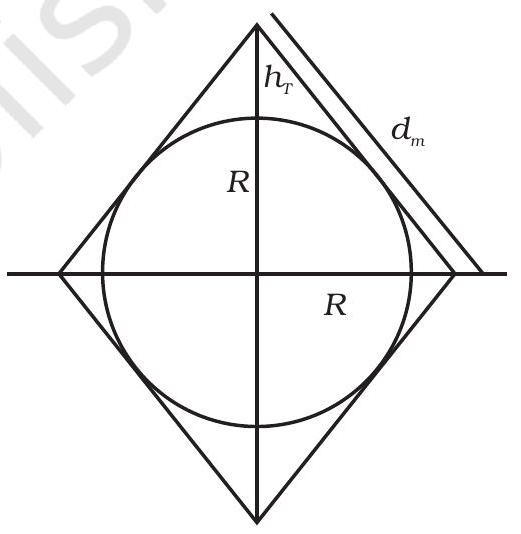
क्योंकि स्थानिक तरंग आवृत्ति का उपयोग होता है, इसलिए $\lambda«h_T$, इसलिए केवल टावर ऊचाई को ध्यान में लिया जाता है।

तीन आयामों में, 6 एंटीना टावरों की ऊचाई $h_T=R$ होगी।

~~ 15.24 $एफ_1$ तरंगमंडल के लिए

$5 \times 10^{6}=9(N _{\max })^{1 / 2}$ या $N _{\max }=(\frac{5}{9} \times 10^{6})^{2}=3.086 \times 10^{11} , m^{-3}$

$एफ_2$ तरंगमंडल के लिए

$8 \times 10^{6}=9(N _{\max })^{1 / 2}$ या

$N _{\max }=(\frac{8}{9} \times 10^{6})=7.9 \times 10^{11} , m^{-3}=7.9 \times 10^{11} , m^{-3}$.

~~ 15.25 $\omega_c-\omega_m, \omega_c$ और $\omega_c+\omega_m$ में से केवल $\omega_c+\omega_m$ या $\omega_c-\omega_m$ में जानकारी होती है।

इसलिए लागत को कम किया जा सकता है द्वारा $\omega_c+\omega_m, \omega_c-\omega_m$ प्रेषित करके, दोनों $\omega_c+\omega_m$ और $\omega_c-\omega_m$

~~ 15.26

(i) $\frac{I}{I_o}=\frac{1}{4}$, इसलिए $\ln (\frac{1}{4})=-\alpha x$

या $\ln 4=$ ax या $x=(\frac{\ln 4}{\alpha})$

(ii) $lolog _{10} \frac{I}{I_o}=-\alpha x$ जहां $\alpha$ किलोमीटर में फीटने वाली घटना है।

यहां $\frac{I}{I_o}=\frac{1}{2}$

या $10 \log (\frac{1}{2})=-50 \alpha$ या $\log 2=5 \alpha$

या $\alpha=\frac{\log 2}{5}=\frac{0.3010}{5}=0.0602 , डीबी / किमी$

~~ 15.27 $ \frac{2 x}{\text{ समय }}=$ वेग

$2 x=3 \times 10^{8} , मी / सेक \times 4.04 \times 10^{-3} , सेक$

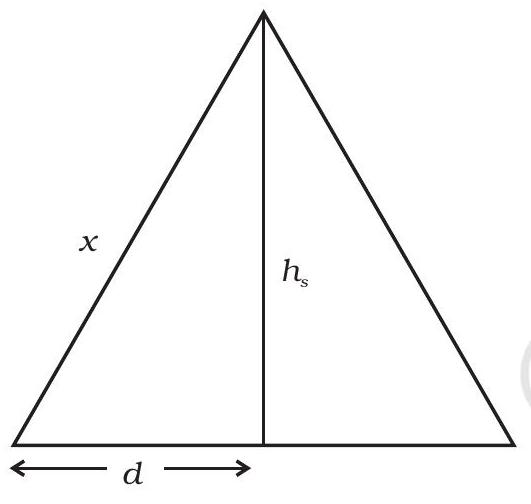
$x=\frac{12.12 \times 10^{5}}{2} , मी=6.06 \times 10^{5} , मी=606 , किमी$

$ड^{2}=x^{2}-h_s^{2}=(606)^{2}-(600)^{2}=7236 ; ड=85.06 , किमी$

ही स्रोत और प्राप्तकर्ता के बीच की दूरी $= 2 डी \

(iv) अधिक संकेतों को सुलभ करने के लिए बैंडविड्थ और ω_c बढ़ाएं। यह दिखाता है कि बड़े कैरियर फ़्रिक्वेंसी से अधिक जानकारी (अधिक ω_m) को भोगोल पर ले जाने में सक्षम होता है और जो कि बैंडविड्थ को बढ़ाएगा।

~~ 15.30 $f_m = 1.5 kHz, \frac{1}{f_m} = 0.7 \times 10^{-3} s$

$f_c = 20 MHz, \frac{1}{f_c} = 0.5 \times 10^{-7} s$

(i) $R C = 10^{3} \times 10^{-8} = 10^{-5} s$

इसलिए, $\frac{1}{f_c} < R C < \frac{1}{f_m}$ को पूरा होता है

इसलिए इसे डिमॉड्यूलेट किया जा सकता है।

(ii) $R C = 10^{4} \times 10^{-8} = 10^{-4} s$।

यहां भी $\frac{1}{f_c} « R C < \frac{1}{f_m}$।

तो यह भी डिमॉड्यूलेट किया जा सकता है।

(iii) $R C = 104 \times 10^{-12} = 10^{-8} s$।

यहां $\frac{1}{f_c} > R C$ है, इसलिए इसे डिमॉड्यूलेट नहीं किया जा सकता है।