वर्तमान बिजली

अध्याय ३

वर्तमान बिजली

MCQ I

~~ ३.१ एक विद्युतधारी तार (विद्युत $I$ की धारा) को एक वृत्ताकार में मानें। ध्यान दें कि जब विद्युत प्रगति करती है, तो j की दिशा (विद्युत घनत्व) बिल्कुल बदल जाती है, जबकि विद्युत $I$ परिणामस्वरूप प्रभावित नहीं होता है। यह कारणबद्ध उद्यम (एजेंट) है

(a) emf का स्रोत।

(b) वायुमंडल द्वारा पैदा की गई विद्युत क्षेत्र।

(c) तार की सतह पर रची गई चार्जों द्वारा उठाये जाने वाले चार्जों के पश्चात्प विभाजन द्वारा उन्हें बिल्कुल सही तरीके से धक्का देने वाले चार्ज।

(d) आगे चार्जेस।

~~ ३.२ $emf \varepsilon_1$ और $\varepsilon_2(\varepsilon_2>\varepsilon_1)$ और आंतरिक प्रतिरोध $r_1$ और $r_2$ के साथ दो बैटरी समान्य रूप से छाने के लिए कनेक्ट किए जाते हैं, जैसा चित्र 3.1 में दिखाया गया है।

(a) इकाई emf $\varepsilon_{eq}$ औसतन $\varepsilon_1$ और $\varepsilon_2$ के बीच होता है, अर्थात $\varepsilon_1<\varepsilon_{eq}<\varepsilon_2$।

चित्र ३.१

(b) इकाई emf $\varepsilon_{eq}$ $\varepsilon_1$ से छोटा होता है।

(d) $\varepsilon_{eq}$ आंतरिक प्रतिरोध $r_1$ और $r_2$ से अपेक्षाकृत निर्भर नहीं होता है।

~~ ३.३ एक मीटर ब्रिज का उपयोग करके एक प्रतिरोध $R$ को मापा जाना है। छात्र ने मानक प्रतिरोध $S$ को $100 \Omega$ के रूप में चुना है। उसने $l_1=2.9 cm$ पर शून्य बिंदु पाया है। उसे सुधार करने के लिए कौन सा उपयोगी तरीका है?

(a) उसे $l_1$ को और सटीकता से मापना चाहिए।

(b) उसे $S$ को $1000 \Omega$ में बदलना चाहिए और प्रयोग को दोहराना चाहिए।

(d) वह एक मीटर ब्रिज के साथ एक नई सुधारी हुई माप की आशा छोड़ देना चाहिए।

~~ ३.४ एक प्यामीटर के द्वारा लगभग $5 V$ और $10 V$ के बिजली को यथार्थ संयोजित किया जाना है, जो कि $400 cm$ के लंबाई का है।

(a) प्यामीटर की बैटरी को $8 V$ की वोल्टेज होनी चाहिए।

(b) प्यामीटर की बैटरी की वोल्टेज $15 V$ हो सकती है और $R$ को समायोजित किया जाए ताकि तार पर क्षेत्र का प्रावृद्धि $10 V$ से थोड़ी सी अधिक हो।

(d) प्यामीटर आमतौर पर प्रतिरोधों को तुलना में उपयोग करने के लिए होता है और न कि वोल्टेज।

~~ ३.५ एक धातु का रॉड जिसकी लंबाई $10 \ cm$ है और आयताकार क्रॉस-ध्वनि $1 cm \times \frac{1}{2} cm$ है, को एक बैटरी से जोड़ा जाता है जो विपरीत मुखों के बीच होती है। प्रतिरोध होगा

(a) जब बैटरी को $1 cm \times \frac{1}{2} cm$ मुखों के बीच जोड़ा जाता है।

(b) जब बैटरी को $10 cm \times 1 cm$ मुखों के बीच जोड़ा जाता है।

(d) तीनों मुखों के बिना उसी होगा।

3.6 एक संचालक में धारिति को किस इलेक्ट्रॉन की विशेषता निर्धारित करती है? (a) केवल ड्रिफ्ट वेगता। (b) केवल थर्मल वेगता। (c) ड्रिफ्ट वेगता और थर्मल वेगता दोनों। (d) न तो ड्रिफ्ट वेगता और न थर्मल वेगता।

MCQ II

~~ 3.7 किर्चहोफ के जंक्शन नियम एक प्रतिबिंब है (a) धारिति घनत्व वेक्टर के संरक्षण। (b) चार्ज के संरक्षण। (c) यह तथ्य कि एक चार्जित कण जंक्शन प्रवेश करते समय जिस के साथ प्राणघात आता है, वह चार्जित कण जंक्शन छोड़ते समय उसी के साथ अचल (एक वेक्टर के रूप में) है। (d) चार्जित कणों का संचय जंक्शन पर नहीं होता है।

~~ 3.8 फिग़ 3.2 में दिखाए गए एक सरल सर्किट का विचार करें। $R^{\prime}$ एक परिवर्तनीय प्रतिरोध $R^{\prime}$ को $R_0$ से अनंत तक बदल सकती है। $r$ बैटरी का आंतरिक प्रतिरोध है $(r « R « R_0)$। (a) $AB$ पर संतति घटाव लगभग स्थिर है जब $R^{\prime}$ बदलती है। (b) $R^{\prime}$ के माध्यम से धारण कर रही धारा तापनिक रूप में स्थिर होती है जब $R^{\prime}$ बदलती है। (c) धारा $I$ $R^{\prime}$ पर आस्थायी रूप में निर्भर करती है। (d) $I \geq \frac{V}{r+R}$ हमेशा।

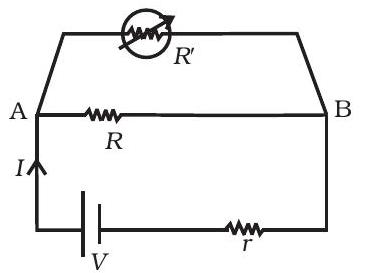फिग़ 3.2

~~ 3.9 सेमीकंडक्टर, इंस्युलेटर्स और धातुओं की प्रतिरोधिता $\rho(T)$ का तापमान निर्भरता तकरार मुख्य आधारित है (a) धारक के संख्या तापमान $T$ के साथ परिवर्तित हो सकती है। (b) दो संयोजन में दो सदीय संक्रमण के बीच की अवधि तापमान $T$ पर निर्भर हो सकती है। (c) धातु की लंबाई तापमान $T$ की एक फ़ंक्शन हो सकती है। (d) धारक की भार तापमान $T$ की एक फ़ंक्शन होती है।

~~ 3.10 गेहूंस्तोन सेतु (फिग़ 3.25) का उपयोग करके एक अज्ञात प्रतिरोध $R$ का मापन किया जाना है। दो छात्र दो तरीकों से प्रयोग करते हैं। पहला छात्र $R_2=10 \Omega$ और $R_1=5 \Omega$ लेता है। दूसरा छात्र $R_2=1000 \Omega$ और $R_1=500 \Omega$ लेता है। मानक हाथ में, दोनों छात्र $R_3=5 \Omega$ लेते हैं।

दोनों ही छात्रों को त्रुटि के अन्दर $R=\frac{R_2}{R_1} R_3=10 \Omega$ मिलता है।

(a) दोनों छात्रों के मोल त्रुटि समान हैं। (b) मोल त्रुटि माप की सटीकता पर मोल त्रुटि का प्रभाव पड़ती है। (c) अगर छात्र बड़े मानों का उपयोग करते हैं तो हथौड़ी के माध्यम से धारा फीबल होगी। यह निर्धारित करना और मुक्त बिंदु को सटीकता से निश्चित करना मुश्किल होगा। (d) गेहूंस्तोन सेतु एक बहुत सटीक उपकरण है और मोल त्रुटि की कोई ग़लती नहीं होती है।

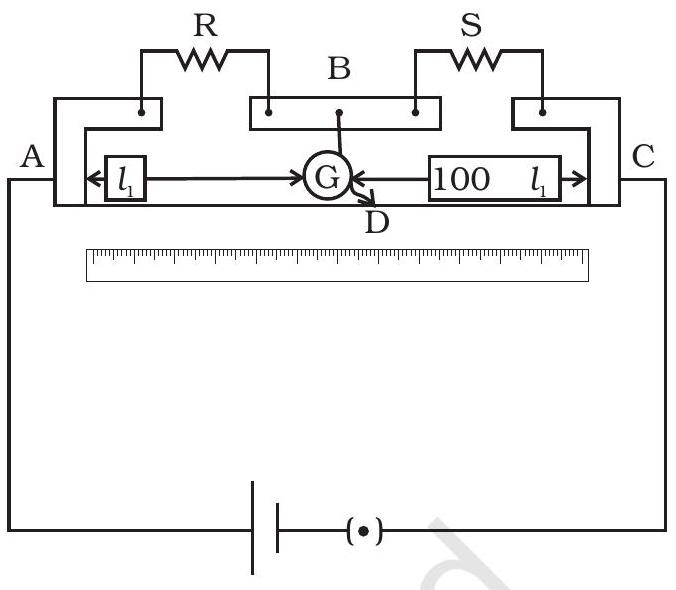
~~ 3.11 मीटर सेतु में बिंदु $D$ एक शांत बिंदु है (फिग़ 3.3)। (a) इस संख्या सेतु के इस सेट के लिए कोई और शांत बिंदु नहीं हो सकता है। (b) जब जॉकी मीटर तार के बायां बिंदु पर संपर्क करती है, तो धारा तार से $B$ की ओर बहती है। (c) जब जॉकी मीटर तार के दाहिने बिंदु पर संपर्क करती है, तो धारा तार से $B$ की ओर जलिपित होती है। (d) $R$ बढ़ाने पर, शांत बिंदु दाहिने की ओर हिलता है।

हालांकि, परिवर्तनशक्ति से जुड़े यहां रेसिस्टर के परंपरागत या इकाई त्वचा के उत्पादन के लिए प्रयुक्त समग्र आर, पूरा और अगर दोनों में एक बड़ी विवशता लागू होती है। यह दर्शाता है कि द्वीपीय कस्तूरबा आधारित आपूर्ति विद्युत संकेताक्षेत्रों के प्रयोग की अद्भुतता को समझने के लिए आवश्यकता होती है, क्योंकि संकेताक्षेत्र का उत्पादन सभी युक्तियों का अनुमोदन और ग्राहकों के लिए साधारित बनाने के लिए आवश्यक है। इसलिए, ऐसा करने के कारण, सासंदित्व एक क्रमबद्धता प्रणाली की जरूरत है ताकि एक संचार समीकरण को अपनाने से इनकार न किया जा सके।

हमें सबसे पहले यह जानने की आवश्यकता होती है कि क्या संचार में चार्ज के पारगमन पर संरचना का मान व्याप्त होता है। यह संबंधित कारण है कि व्याप्तिकीय ध्यान दिया जाएगा और दौरी द्वारा प्रतिस्थापित होती है।

तब हम एक मुख्य प्रश्न का साधारित सारांशः From the choices, the null-point method in a Wheatstone bridge has several advantages. It is highly accurate for measuring resistance since it balances the unknown resistance with a standard resistance. Additionally, the null-point method is not affected by any variations in the power supply voltage. However, to calculate the unknown resistance using any other method, additional measurements such as voltage drops or current flows would be required.

अगला प्रश्न है कि इंधन कीमत गृहों के रचना में बहुत महत्वपूर्ण होती है। कूपर तारों की द्वारा इस्तेमाल होने वाली अपनी जड़ों को एल से तारों से जोड़े जा सकते हैं. इसमें विवेचना के अनुभव को ध्यान में रखकर की संकेताक्षेत्र क्षेत्रों और तारों की कार्य सुरक्षित रचना में सरलता हो सकती है. यह अधिकतम आधार पर अपनी चुनौतियों के मद्देनजर तारों के प्रयोग का करण हो सकता है।

ध्यान देने योग्य है कि क्योंकि अच्छा धातुविद्युत सन्मान उन इंधन मांसद तारी को समयबद्ध रूप से ईंधन करने के लिए उपयोग करना पड़ता है.

आगे बढ़ते हुए, यहां ध्यान में रखने योग्य है कि तारों के ऊर्जा संकेताक्षेत्र हेतु दान्तों का उपयोग क्यों अधिकतम प्राथमिकता होता है.

अंतिम प्रश्न है कि धातुविभजित कोइल का निर्माण करने के लिए क्यों आधारभूत ऊर्जा का उपयोग होता है।

अगर एक उपकरण द्वारा ऊर्जा प्रेषित करनी हो तो तार वाले प्रेषण केबल के रैसिस्टन सी के प्रति उबाष्ट को खो दे तो R से उत्पन्न खोयी गयी ऊर्जा की क्षमता और इसे कैसे कम कर सकते हैं।

$AB$ एक प्रतिरोध तार है (चित्र 3.4)। यदि $R$ का मान वृद्धि होता है, तो क्या एक इतर दिशा में संतुलन बिन्दु $J$ को विस्तार करेगा?

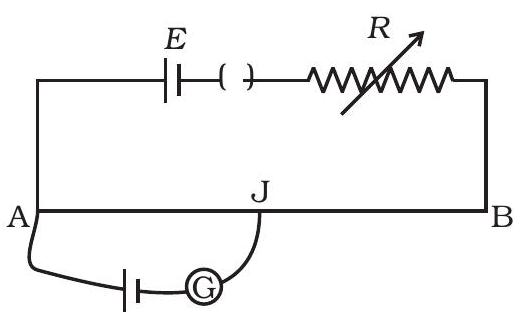प्रतिरोध तार का चित्र 3.4

यदि कस्तूरबा के साथ एक प्रयोग करने के दौरान (चित्र 3.5) पता चलता है कि विस्तार एक-तरफा होता है और (i) तार के एक से दूसरे सिरे $A$ से जब $B$ की ओर जाता है तो विस्तार कम होता है; (ii) जब जॉकी अंत $B$ की ओर ले जाती है तो विस्तार बढ़ता है।

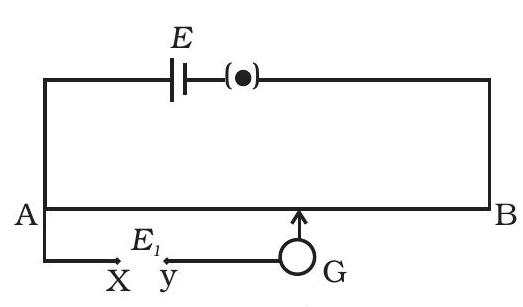प्रतिरोध तार का चित्र 3.5

(i) नियमानुसार, संख्यानुसार पोजिटिव या ऋणात्मक कस्तूरब का टर्मिनल $ई_1$ को केंद्र $X$ में कर रहा है और ई_1 ई के साथ कैसे संबंधित है?

(ii) ज्योग ने संचार केबल में टर्मिनल $ई_1$ को किस दिशा में कर रखा है?

~~ 3.21 एक सेल की इमफ $E$ और आंतरिक प्रतिरोध $र$ के पार संचारित बाहरी प्रतिरोध $आर$ के साथ संपर्कित होती है। $ने संकेताक्षेत्र र,बनाने के लिए बिज्ञापन का एक चार्ट बनाने की प्लान (P.D) इनकार किया है, क्योंकि $र$ प्रतिरोध मज़बूत है। समझिए?

३.२४ शेकल ३.६ में दिखाए गए सर्किट में दो कक्ष एक दूसरे के विपरीत जुड़े हुए हैं। कक्ष $ई_१$ की emf $६ वी$ और आंतरिक प्रतिरोध $२ ओम$ है; कक्ष $ई_२$ की emf $४ वी$ और आंतरिक प्रतिरोध $८ ओम$ है। बिंदु $ए$ और $बी$ के बीच की संभावित भेद ढूंढें।

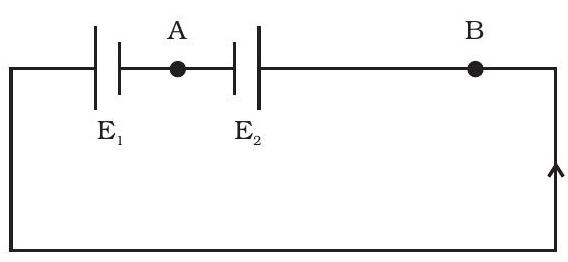शेकल ३.६

~~ ३.२५ एक ही emf $ई$ लेकिन आंतरिक प्रतिरोध $र_१$ और $र_२$ वाले दो कक्षों को बाह्य विद्युत प्रतिरोधक $आर$ के साथ दोनों जोड़ा जाता है (शेकल ३.७)। पहले कक्ष के टर्मिनल के बीच की संभावित तार के शून्य हो जाने के लिए $आर$ की मान क्या होनी चाहिए।

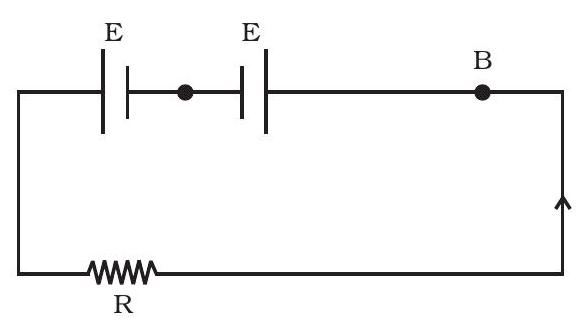शेकल ३.७

~~ ३.२६ दो चालक उद्देश्य में एक जैसी सामग्री से बनाए गए हैं और एक ही लंबाई है। चालक एक $1 mm$ व्यासवृत्त (diameter) द्वारा कठोर तार है। चालक बी है $2 mm$ व्यासवृत्त की खोखली ट्यूब है और $1 mm$ अंतरिक्ष है। $R_A$ से $R_B$ के अनुपात (Ratio) का पता लगाएं।

~~ ३.२७ सोचिए एक सर्किट को केवल प्रतिरोधन (Resistance) और बैटरी से मिलकर होता है और हमें सभी वोल्टेज (Voltages) और सभी प्रतिरोधों (Resistances) को दोगुना करना है (या इसे $n$ गुणा करना है)। दिखाएं कि प्रवाह (Currents) बिना बदले हुए होते हैं। इसे कक्ष के उदाहरण 3 .7 के लिए एनसीईआरटी कक्ष। १२ की पाठयपुस्तक में करें।

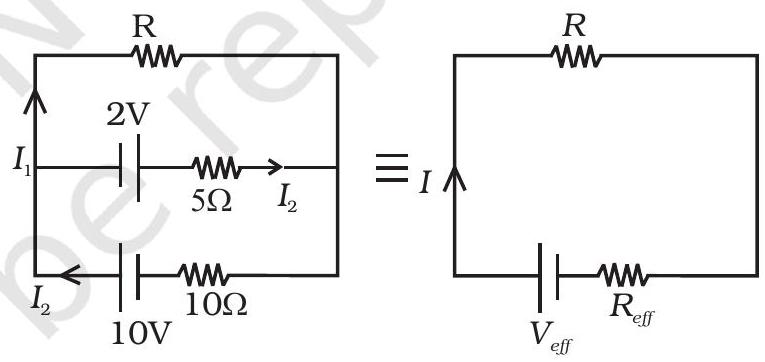
~~ ३.२८ मानव वोल्टेज $10 V$ और $2 V$ और आंतरिक प्रतिरोध $10 \Omega$ और $5 \Omega$ के दो बैटरी अवलंबित हैं, पैरालेल में संगठन के सकारात्मक सिरे से $10 V$ बैटरी के सकारात्मक सिरे से $2 V$ बैटरी के नकारात्मक सिर के साथ जुड़े हुए हैं (देखें चित्र 3.८)। संयुक्तिक वोल्टेज और संयुक्तिक प्रतिरोध का पता लगाएं। 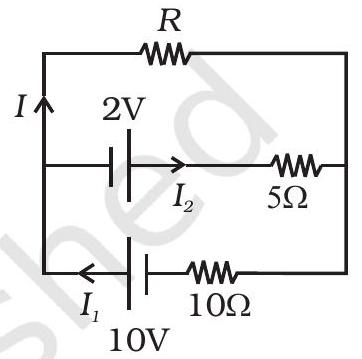शेकल 3.८

~~ ३.२९ एक कमरे में प्रतिदिन 5 घंटे चलने वाला $AC$ बिजली प्रयोगित होता है जिसमें वोल्टेज $220 V$ होता है। कमरे की वाइयरिंग $Cu$ की $1 mm$ त्रिज्या (radius ) वाली होती है और लंबाई $10 m$ होती है। प्रतिदिन का बिजली की खपत 10 वाणिज्यिक यूनिट होती है। इसमें कितना हिस्सा तारों में जूल हीटिंग में चलता है? एक ही आयाम वाले एल्यूमीनियम की वायरिंग हो जाए तो क्या होगा?

$[\rho _{cu}=1.7 \times 10 _{\Omega m}^{-8}, \rho _{Al}=2.7 \times 10^{-8} \Omega m]$

~~ ३.३० एक प्रयोग में, पोटेंशियोमीटर के साथ $V_B=10 V$ होता है। $R$ को $50 \Omega$ कर दिया जाता है (शेकल 3.९)। एक छात्र द्वारा एक बैटरी के वोल्टेज $E_1$ (इसकी क़ेमत लगभग ८ वोल्ट) मापने की कोशिश करने पर कोई शून्य बाइंडिंग बिंदु मुमकिन नहीं है। फिर उन्होंने $R$ को $10 \Omega$ पर घटा दिया और पोटेंशियोमीटर की अंतिम $(4^{\text{th }})$ खंभा में शून्य बाइंडिंग बिंदु मिला है। पोटेंशियोमीटर वायर की प्रतिरोध और इस दूसरे मामले में वायर के ज़र्रे प्रति लंबाई के भीतर बिज़ल गिरावट (potential drop) की गणना करें।

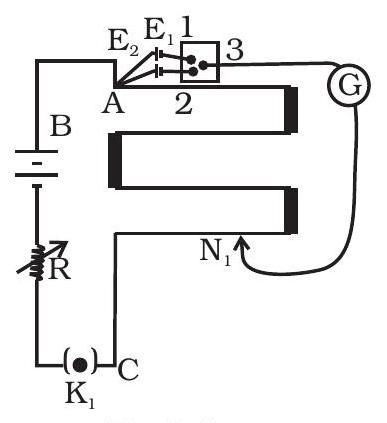शेकल 3.९

कॉन्टेंट: 3.31 (क) चित्र 3.10 में सर्किट को विचार करें। आदिक्षेत्र से चल रहे इलेक्ट्रॉन्स द्वारा कितनी ऊर्जा अवशोषित होती है (उष्णायन की गति को अनदेखा करें) से ड्रिफ्ट वेग की स्थिति तक?

(ख) इलेक्ट्रॉन का थर्मल ऊर्जा में ऊर्जा छोड़ते हैं। एक सेकंड में ऊर्जा के साथ कितना समय संलग्न करेंगे (क)? $n=$ इलेक्ट्रॉनों की संख्या $/$ आयतन $=10^{29} / m^{3}$, सर्किट की लंबाई $=10 cm$, संकरण-खंड $=A=(1 mm)^{2}$

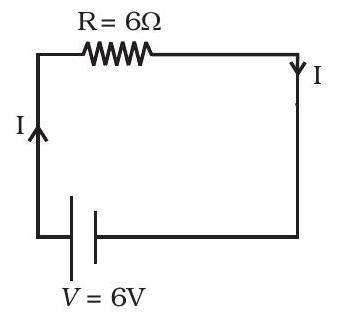Figure 3.10

अध्याय 3

~~ 3.1 (क)

~~ 3.2 (ख)

~~ 3.3 (ग)

~~ 3.4 (ख)

~~ 3.5 (क)

~~ 3.6 (क)

~~ 3.7 (ख), (द)

~~ 3.8 (क), (द)

~~ 3.9 (क), (ख)

~~ 3.10 (ख), (ग)

~~ 3.11 (क), (ग)

~~ 3.12 जब एक इलेक्ट्रॉन एक जंक्शन के पास आता है, तो साथ ही-साथ उनको सामान्य रूप से प्रतिदिक्षित करने वाले $\mathbf{E}$ के अतिरिक्त (जो चलन वेग $\boldsymbol{{}v}_d$ को सुरक्षित रखता है) तेजी से विद्युतीय चार्जों की सतह पर भराई होती है। ये विद्युतीय क्षेत्र गतिकी की दिशा को बदलते हैं।

~~ 3.13 आरामदायक समय इलेक्ट्रॉनों और आयनों की वेगों पर निर्भर करेगा। लागू विद्युत आयाम इलेक्ट्रॉनों की वेगों पर $1 mm / s$ के आदेश में प्रभाव नहीं डालता है। हालांकि, $T$ में परिवर्तन, वेगों पर $10^{2} m / s$ के आदेश में प्रभाव डाल सकता है। इससे $\tau$ में प्रमुख बदलाव हो सकता है।

[ $\rho=\rho(E, T)$ जिसमें $E$ की व्यापकता सामान्य आवेदनिक वोल्टेज के लिए अनदेखी जाती है।]

~~ 3.14 वीटस्टोन पुलिये में शून्य बिंदु विधि की फायदा यह है कि गेल्वैनोमीटर की प्रतिरोधकता भार से संतुष्ट नहीं करती है और रिजिस्टेंसेज और गेल्वैनोमीटर और गेल्वैनोमीटर की आंतरिक प्रतिरोधकता में व्यापार नहीं होता है। $R _{\text{अज्ञात }}$ की गणना की जा सकती है सर्किट पर किर्चहोफ के नियमों को लागू करके। हमें रेजिस्टेंसेज और गेल्वैनोमीटर और गेल्वैनोमीटर की सभी धाराओं को और गेल्वैनोमीटर की आंतरिक प्रतिरोधकता के लिए अतिरिक्त सटीक माप की आवश्यकता होती है।

~~ 3.15 धातु स्ट्रिप की कम प्रतिरोधता होती है और पोटेंटिओमीटर की लंबाई $l_1$ में गिना नहीं जाना चाहिए। केवल सीधे खंडों के माध्यम से उनकी लंबाई को मापा जाता है (प्रत्येक मीटर की लंबाई के)। इसे सेंटीमीटर गिनती या मीटर रूलर की सहायता से आसानी से किया जा सकता है और सटीक मापन करता है।

~~ 3.16 दो परिवेशनों को ध्यान में रखना आवश्यक है: (ग) धातु की लागत और (ख) धातु की अच्छी प्रवाहिता। लागत कारक चांदी को अवरुद्ध करता है। $Cu$ और $Al$ दूसरे सर्वश्रेष्ठ प्रवाहक हैं।

~~ 3.17 ऑलॉयों की प्रतिरोधता का तापमान सहिष्णुता (कम तापमान प्रतिक्रिया) होती है और उच्च संक्रमणात्मकता होती है।

~~ 3.18 वेदनशीलता खोई जाती है $P_C=I^{2} R_C$

यहां $R_C$ कनेक्टिंग तार की प्रतिरोध है।

$P_C=\frac{P^{2}}{V^{2}} R_C$

$P_C$ कम करने के लिए, ऊर्जा उच्च वोल्टेज पर प्रेषित की जानी चाहिए।

3.19 यदि $R$ बढ़ाया जाता है, तो तार में धारण की धारा कम होगी और इसलिए ही विभव ढलन भी कम होगी, जिससे संतुलन लंबाई में वृद्धि होगी। इसलिए, जे बी की ओर शिफ्ट हो जाएगा।

~~ 3.20 (i) $E_1$ की सकारात्मक टर्मिनल को $X$ पर कनेक्ट किया गया है और $E_1>E$।

(ii) $E_1$ की नकारात्मक टर्मिनल को $X$ पर कनेक्ट किया गया है।

~~ 3.21

~~ 3.22 $ I=\frac{E}{R+n R} ; \frac{E}{R+\frac{R}{n}}=10 I$

$\frac{1+n}{1+\frac{1}{n}}=10=\frac{1+n}{n+1} n=n$

$\therefore n=10$.

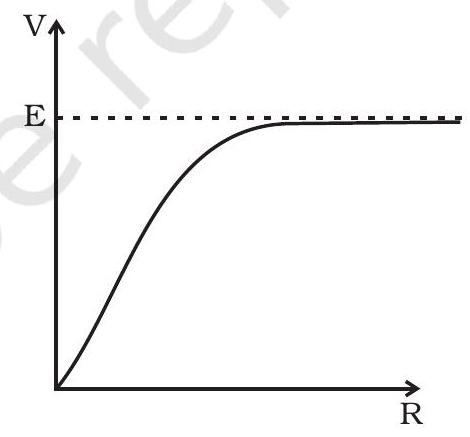
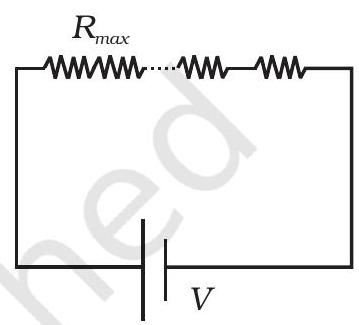
~~ 3.23 $ \frac{1}{R_p}=\frac{1}{R_1}+\ldots \ldots+\frac{1}{R_n}, \quad \frac{R _{\min }}{R_P}=\frac{R _{\min }}{R_1}+\frac{R _{\min }}{R_2}+\ldots \ldots+\frac{R _{\min }}{R_n}>1$

और $R_S=R_1+\ldots \ldots+R_n \geq R _{\max }$।

चित्र (ब) में, $R _{\min }$ तस्वीरा में एक समकरण रस्ता प्रदान करता है। लेकिन इसके अलावा, बाकी $(n-1)$ रेजिस्टर्स में $(n-1)$ मार्ग हैं। तस्वीर (ब) में धारा तस्वीर (ए) में धारा से अधिक है। तस्वीर में प्रभावी प्रतिरोध $R _{\min }$ से कम है। दूसरा सर्किट स्वतः ही अधिक प्रतिरोध प्रदान करता है। आप तस्वीर (क) और (ड) का उपयोग कर सकते हैं और साबित कर सकते हैं कि $R_s>R _{\max }$।

(ए)

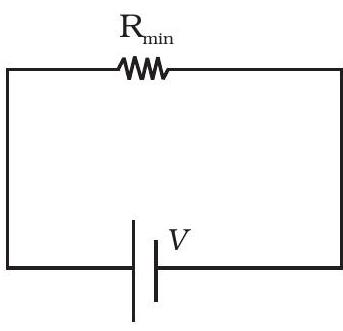
(ब)

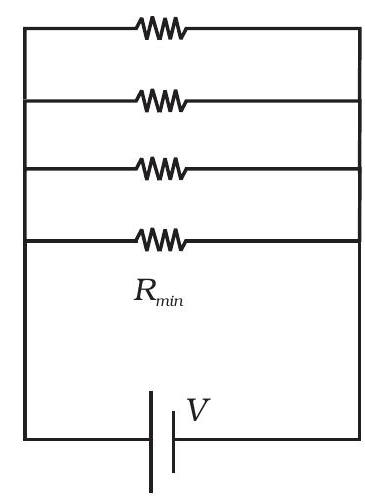
(क)

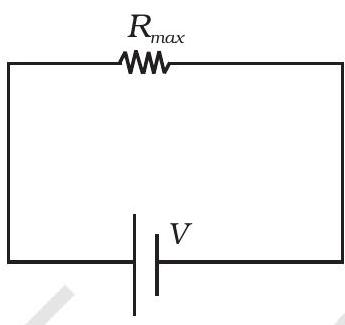
(ड)

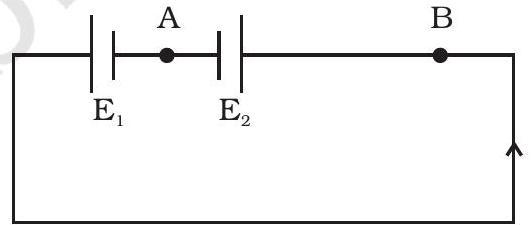
~~ 3.24 $ \quad I=\frac{6-4}{2+8}=0.2 A$

$E_1$ के प्रति विभव ड्राप = $6-0.2 \times 2=5.6 V$

$E_2$ के प्रति विभव ड्राप = $V _{AB}=4+0.2 \times 8=5.6 V$

बिंदु $B$ बिंदु $A$ से अधिक विभव पर है

~~ 3.25 $\quad I=\frac{E+E}{R+r_1+r_i}$

$V_1=E-I r_1=E-\frac{2 E}{r_1+r_2+R} r_1=0$

या $E=\frac{2 E r_1}{r_1+r_2+R}$

$1=\frac{2 r_1}{r_1+r_2+R}$

$r_1+r_2+R=2 r_1$

$R=r_1-r_2$

~~ 3.26

$R_A=\frac{\rho l}{\pi(10^{-3} \times 0.5)^{2}}$

$R_B=\frac{\rho l}{\pi[(10^{-3})^{2}-(0.5 \times 10^{-3})^{2}]}$

$\frac{R_A}{R_B}=\frac{(10^{-3})^{2}-(0.5 \times 10^{-3})^{2}}{(.5 \times 10^{-3})^{2}}=3: 1$

~~ 3.27 हम किसी शाखा $R$ के लिए पूरे नेटवर्क को एक साधारित करने के लिए सोच सकते हैं जैसा कि चित्र में दिखाया गया है।

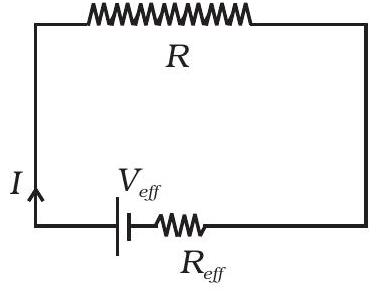
तब $R$ के माध्यम से धारण की धारा $I=\frac{V _{\text{eff }}}{R _{\text{eff }}+R}$ होगी।

वातावरणीय रूप से $V _{\text{दिंचनी }}=V _{\text{दिंचनी }}(V_1, V_2, \ldots \ldots V_n)$ का आयाम वोल्टेज है और $R _{\text{दिंचनी }}=R _{e f f}(R_1, R_2, \ldots \ldots . R_m)$ का आयाम प्रतिरोध है।

इसलिए अगर सभी को $n$ गुणा बढ़ा दिया जाए

$V _{e f f}^{\text{नया }}=n V _{\text{दिंचनी }}, R _{e f f}^{\text{नया }}=n R _{\text{दिंचनी }}$

और $R^{\text{नया }}=n R$।

इस प्रकार धारा वही रहती है।

~~ 3.28 किर्चहोफ के संयोजन नियम का उपयोग करें:

$I_1=I+I_2$

किर्चहोफ के घुमाव नियम देता है:

$10=I R+10 I_1 \ldots(i)$

$2=5 I_2-R I=5(I_1-I)-R I$

$4=10 I_1-10 I-2 R I \ldots$. (ii)

(i) - (ii) से $\Rightarrow 6=3 R I+10 I$ या $2=I(R+\frac{10}{3})$

$2=(R+R _{दिंचनी}) I$ को $V _{\text{दिंचनी }}=(R+R _{e f f}) I$ के साथ तुलना करें

और $V _{\text{दिंचनी }}=2 V$

$R _{दिंचनी}=\frac{10}{3} \Omega$।

~~ 3.29 विद्युत खपत $=2$ इकाइयाँ $/$ घंटे $=2 किलोवॉट=2000 जूल / सेकंड$

$I=\frac{P}{V}=\frac{2000}{220} \simeq 9 A$

तार में विद्युत खोना $=R I^{2} जूल / सेकंड$

$ \begin{aligned} & =\rho \frac{l}{A} I^{2}=1.7 \times 10^{-8} \times \frac{10}{\pi \times 10^{-6}} \times 81 जूल / सेकंड \\ & \simeq 4 जूल / सेकंड \\ & =0.2 % \end{aligned} $

ऐल्यूमिनियम तार में विद्युत खोना $=4 \frac{\rho _{A l}}{\rho _{C u}}=1.6 \times 4=6.4 जूल / सेकंड=0.32 %$

~~ 3.30 पोटेंशियोमीटर तार की प्रतिरोधता $R^{\prime}$ हो।

$\frac{10 \times R^{\prime}}{50+R^{\prime}}<8 \Rightarrow 10 R^{\prime}<400+8 R^{\prime}$

$2 R^{\prime}<400$ या $R^{\prime}<200 \Omega$।

$\frac{10 \times R^{\prime}}{10+R^{\prime}}>8 \Rightarrow 2 R^{\prime}>80 \Rightarrow R^{\prime}>40$

$\frac{10 \times \frac{3}{4} R^{\prime}}{10+R^{\prime}}<8 \Rightarrow 7.5 R^{\prime}<80+8 R^{\prime}$

$R^{\prime}>160 \Rightarrow 160<R^{\prime}<200$।

किसी भी R’ के बीच $160 \Omega$ और $200 \Ω$ तक प्राप्त किया जा सकता है।

तार के $400 सेमी$ पर्याप्ततम वोल्टेज गिरावट $>8 V$ होगी।

तार के $300 सेमी$ पर्याप्ततम वोल्टेज गिरावट $<8 V$ होगी।

$ \phi \times 400>8 V(\phi \to \text{ पोटेंशियल ढाल }) $

$ \begin{aligned} & \phi \times 300<8 V \\ & \phi>2 V / m \end{aligned} $

$ <2 \frac{2}{3} V / m $

~~ 3.31

(a) $I=\frac{6}{6}=1 A=n e v_d A$

$ \begin{aligned} v_d= & \frac{1}{10^{29} \times 1.6 \times 10^{-19} \times 10^{-6}}=\frac{1}{1.6} \times 10^{-4} m / s \\ K . E & =\frac{1}{2} m_e v_d^{2} \times n A l \\ & =\frac{1}{2} \times 9.1 \times 10^{-31} \times \frac{1}{2.56} \times 10^{-8} \times 10^{29} \times 10^{-6} \times 10^{-1} \simeq 2 \times 10^{-17} J \end{aligned} $

(b) आम्षिक हानि $=R I^{2}=6 \times 1^{2}=6 J / s$

इलेक्ट्रॉनों की सभी की किनेटिक ऊर्जा $\frac{2 \times 10^{-17}}{6} s \simeq 10^{-17} s$ में ही खोई जाएगी।

पिछला

संचार तंत्र

अगला

विकिरण और पदार्थ की दोहरी प्रकृति

भौतिक विज्ञान (कक्षा-12) | एनसीईआरटी एक्जम्पलर