अध्याय 11

विकिरण और पदार्थ की द्वैत प्रकृति

MCQ I

~~ 11.1 एक कण को ऊचाई $H$ से छोड़ा जाता है। कण की देब्रोगली तत्वावधानी ऊचाई के रूप में होती है

(a) $H$ के अनुपात में

(b) $H$ के १/२ के अनुपात में

(c) $H$ के ० के अनुपात में

(b) $H$ के -१/२ के अनुपात में

~~ 11.2 एक प्रोटॉन को नकले १ मेव ऊर्जा से जुड़े नकल पराभूत करने के लिए फ़ोटन की तरंगदैर्घ्य अनुमानित रूप में होती है

(a) $1.२ नैनोमीटर$

(b) $1.२ × 10^{−3} नैनोमीटर$

(c) $1.२ × 10^{−6} नैनोमीटर$

(d) $1.२ × 10^{1} नैनोमीटर$

~~ 11.3 एक रेला इलेक्ट्रॉन की गोताम ऊर्जा ($E_0$ ऊर्जा के प्रति प्रोटॉन) वाले इलेक्ट्रॉन ऊर्जा एक खाली चैम्बर में रखी किसी धातु की सतह पर आगमित होते हैं। तब (a) कोई इलेक्ट्रॉन छोड़े नहीं जाएंगे क्योंकि केवल फ़ोटन इलेक्ट्रॉन छोड़ सकते हैं।

(b) इलेक्ट्रॉन तो छोड़े जा सकते हैं लेकिन सभी इलेक्ट्रॉन उसी ऊर्जा के साथ।

(c) इलेक्ट्रॉन किसी भी ऊर्जा के साथ छोड़े जा सकते हैं, जिसका अधिकतम होता है $E_0-\phi$ ($\phi$ कार्य उत्सर्जन है)।

(d) इलेक्ट्रॉन किसी भी ऊर्जा के साथ छोड़े जा सकते हैं, जिसका अधिकतम होता है $E_0$।

~~ 11.4 न्सीआरट कक्षा १२ की भौतिकी ताप पुस्तक में चित्र ११.७ को ध्यान से देखें। मान लीजिए एक कण को A पर लगाया गया वोल्टेज बढ़ा दिया गया है। विकिरित तरंग $θ$ पर अधिकतम होगी जो

(a) पहले वाले मान के बड़ी होगी।

(b) पहले वाले मान के समान होगी।

(c) पहले वाले मान के छोटी होगी।

(d) लक्ष्य पर निर्भर करेगी।

~~ 11.5 एक प्रोटॉन, एक न्यूट्रॉन, एक इलेक्ट्रॉन और एक $\alpha$-कण एक ही ऊर्जा होती हैं। तब उनकी देब्रोगली तत्वावधानी तुलना इस प्रकार होती है

(a) $\lambda_p=\lambda_n>\lambda_e>\lambda _{\alpha}$

(b) $\lambda _{\alpha}<\lambda_p=\lambda_n>\lambda_e$

(c) $\lambda_e<\lambda_p=\lambda_n>\lambda _{\alpha}$

(d) $\lambda_e=\lambda_p=\lambda_n=\lambda _{\alpha}$

~~ 11.6 एक इलेक्ट्रॉन संचालितत तेज़ी से गति $\mathbf{v}=v_0 \hat{\mathbf{i}}$ और एक चुंबकीय क्षेत्र $\mathbf{B}=B_0 \hat{\mathbf{j}}$ में होता है। तो इसकी देब्रोगली तात्विक तरंगदैर्घ्य

(a) स्थिर रहेगी।

(b) समय के साथ बढ़ती है।

(c) समय के साथ घटती है।

(d) नियमित रूप से बढ़ती और घटती है।

~~ 11.7 एक इलेक्ट्रॉन (मास $m$ ) जिसकी प्रारम्भिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}(v_0>0)$ है, वह एक विद्युत क्षेत्र $\mathbf{E}=-E_0 \hat{\mathbf{i}}(E_0=.$ स्थिर संख्या $.>0)$ में है। समय $t$ पर इसकी देब्रोगली तत्वावधानी अवधि इस प्रकार दी जाती है

(a) $ \frac{\lambda_0}{(1+\frac{e E_0}{m} \frac{t}{v_0})} $

(b) $\lambda_0(1+\frac{e E_0 t}{m v_0})$

(c) $\lambda_0$

(d) $\lambda_0 t$.

~~ 11.8 एक इलेक्ट्रॉन (मास $m$ ) जिसकी प्रारम्भिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}$ है, वह एक विद्युत क्षेत्र $\mathbf{E}=E_0 \hat{\mathbf{j}}$ में है। अगर $\lambda_0=h / m v_0$ है, तो समय $t$ पर इसकी देब्रॉगली तत्वावधानी अवधि इस प्रकार दी जाती है

(a) $\lambda_0$

(b) $\lambda_0 \sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$

(c) $\frac{\lambda_0}{\sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}}$

(d) $\frac{\lambda_0}{(1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}})}$

MCQ II

~~

11.9 ब्रह्मवैदिक संशोधन अतिरिक्तच अवश्यक होगा जब गतिशक्ति का सूत्र $\frac{1}{2} m v^{2}$, $m c^{2}$ के समान हो जाता है, यहाँ पार्टिकल की भार है। एक इलेक्ट्रॉन के लिए संयुक्त राशि में ब्रह्मवैदिक संशोधन अहम होंगे वहां तक भौतिक लंबदी बेदयन्त्र कहाँ होगी?

(क) $\lambda=10 nm$

(ख) $\lambda=10^{-1} nm$

(ग) $\lambda=10^{-4} nm$

(घ) $\lambda=10^{-6} nm$

~~ 11.10 दो राशि $A _{1 s}$ और $A_2$ जिनकी भारें $m_1, m_2(m_1>m_2)$ हैं, उनकी ब्रह्मवैदिक लंबदी समान है। फिर

(क) उनकी गतिमान समान होंगी।

(ख) उनकी ऊर्जाएँ समान होंगी।

(ग) $A_1$ की ऊर्जा, $A_2$ की ऊर्जा से कम होगी।

(घ) $A_1$ की ऊर्जा, $A_2$ की ऊर्जा से अधिक होगी।

~~ 11.11 एक फोटन की ब्रह्मवैदिक लंबदी एक इलेक्ट्रॉन की ब्रह्मवैदिक लंबदी का दोगुना है। इलेक्ट्रॉन की गति है $v_e=\frac{c}{100}$। तब

(क) $\frac{E_e}{E_p}=10^{-4}$

(ख) $\frac{E_e}{E_p}=10^{-2}$

(ग) $\frac{p_e}{m_e c}=10^{-2}$

(घ) $\frac{p_e}{m_e c}=10^{-4}$।

~~ 11.12 ब्रह्मवैदिक लंबदी वाला एक फोटन विज्ञता में अधिक सत्ता को ध्यान में रखते हुए प्रयुक्तियों में अवरुद्ध होता है। जो बोध माला $n$ फोटन/सेकंड का उत्साद निकालता है शक्आ की में $1 kg$ जल में पानाजल से १०० से $0^{\circ} C$ जल में परिवर्तन किया गया था। चुनिए ऐसा समय $T$।

(क) $n$ बढ़ाने पर कम होगा, $v$ निश्चित रखते हुए।

(ख) $v$ बढ़ाने पर, $n$ निश्चित रखते हुए कम।

(ग) $n$ और $v$ बदलने के साथ निश्चित रहेगा जिसकी $n v=$ सत्यापित की गई।

(घ) $n v$ के उत्पाद के बढ़ने पर ऐसा बढ़ेगा।

~~ 11.13 एक पानी प्रवाहित जीव मूल्य के चालने पर केंद्र के चारों ओर एक समान्य वन चक्र के अंतर्गत तत्व चलता है। भार की ब्रह्मवैदिक लंबदी आमत्रित ब्रह्मवैदिक लंबदी साबित होगी इसका वर्णन नीचे दिए गए बयानों में किसके अधीन गोपनीय ब्रह्मवैदिक लंबदी साबित होने जैसे होंगे?

(क) तत्व केंद्र रचि समतल चालने पर।

(ख) तत्व केंद्र को तड़ित चालने पर।

(ग) जब ब्रह्मवैदिक लंबदी $\lambda_1$ होती है, तब तत्व निकटतम होता है जबकि इसकी मूल्य $\lambda_2$ होती है।

(घ) जब ब्रह्मवैदिक लंबदी $\lambda_2$ होती है, तब तत्व निकटतम होता है जबकि इसकी मूल्य $\lambda_1$ होती है।

VSA

~~ 11.14 एक प्रोटॉन और एक $\alpha$-काणी प्रायसरंजात हो रहे हैं, एक ही वैद्युतिसंधि का उपयोग करते हुए। कथनों को चुनें जिनमें उल्लिखित है कि कैसे दो ब्रह्मवैदिक लंबदी $\lambda_p$ और $\lambda_a$ एक दूसरे से संबंधित हैं?

~~ 11.15 (सूत्रक) फोटोइलेक्ट्रिक प्रभेद का व्याख्यान में हम एक फोटन गति $v$ की एक इलेक्ट्रॉन के साथ टकराते हैं और इसकी ऊर्जा नियमित करते हैं। इससे निकाली जाने वाले अधिकतम ऊर्जा $E _{\max }$ की समीकरण दिया जाता है

$ E _{\max }=h v-\phi_0 $

यहाँ धातु का कार्य नियम $\phi_0$ है। अगर एक इलेक्ट्रॉन 2 फोटन (प्रत्येक की गति $v$) को अवशोषित करता है तो निकाल इलेक्ट्रॉन के लिए अधिकतम ऊर्जा क्या होगी?

(ख) यह सच (दो फोटन अवशोषण) हमारी रुपरेखा के बारे में क्यों नहीं लिया जाता है जो हमने स्टॉप करने की क्षमता के बारे में चर्चा की है?

11.16 वहाँ पदार्थ होते हैं जो छोटी तरंगदैर्घ्य के फोटॉन शोषण करते हैं और लम्बी तरंगदैर्घ्य के फोटॉन उत्पन्न करते हैं। क्या स्थिर पदार्थ हो सकते हैं जो बड़ी तरंगदैर्घ्य के फोटॉन शोषण करते हैं और दिखते हैं छोटी तरंगदैर्घ्य का प्रकाश।

~~ 11.17 क्या सभी इलेक्ट्रॉन जो एक फोटॉन को शोषण करते हैं, वे सभी फोटोइलेक्ट्रॉन के रूप में निकलते हैं?

~~ 11.18 दो प्रकाश स्रोत हैं, प्रत्येक $100 W$ द्वारा उत्सर्जित करते हैं। एक $1 nm$ तरंगदैर्घ्य में X-रे उत्पन्न करता है और दूसरा $500 nm$ प्रकाश उत्पन्न करता है। दिए गए तरंगदैर्घ्य के X-रे के फोटॉनों की संख्या का अनुपात अनुपात ढूँढें?

SA

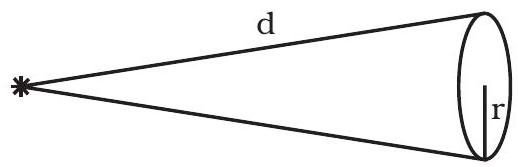
~~ 11.19 फोटोइमिशन के लिए चित्र 11.1 को ध्यान से देखें।

पलटती पलटती-संरक्षण के साथ आप लड़ सकते हैं? ध्यान दें कि प्रकाश (फोटॉन) उत्पन्न हो रहा है जिसमें निकलते इलेक्ट्रॉनों से अलग दिशा में प्राणी होता है।

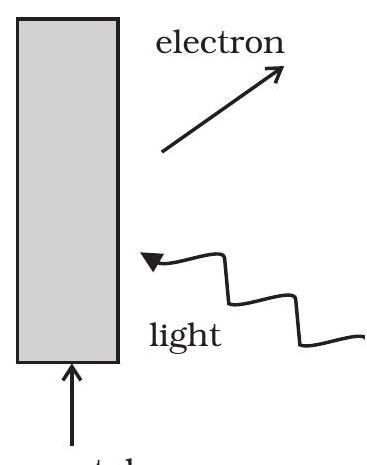चित्र 11.1

~~ 11.20 $600 nm$ तरंगदैर्घ्य के प्रकाश के सामने एक धातु को ध्यान में रखें। $400 snm$ तरंगदैर्घ्य के प्रकाश का उपयोग करने पर इलेक्ट्रॉन की अधिकतम ऊर्जा दोगुनी हो जाती है। eV में कार्याक्षमता ढूँढें।

~~ 11.21 एक इलेक्ट्रॉन को $1 nm$ चौड़ा क्षेत्र में सीमित मानें, हाइजेनबर्ग अनिश्चितता के सिद्धांत का उपयोग करके प्रावृत्ति की अनिश्चितता ढूँढें (NCERT की पाठपुस्तक के Eq 11.12 के अनुसार)। आप $1 nm$ के रूप में स्थान की अस्थिरता $\Delta x$ मान सकते हैं। $p \simeq \Delta p$ मानते हुए, इलेक्ट्रॉन की ऊर्जा का ढूँढें इलेक्ट्रॉन वोल्ट में।

~~ 11.22 एक सामकालीन बीम A और B, समान मात्रा $I$ के साथ, एक स्क्रीन में गिरती हैं। बीम A द्वारा पहुंचा गया फोटॉनों की संख्या बीम B द्वारा पहुंचा गया फोटॉनों की दोगुनी होती है। तो तुम क्या अनुमान लगा सकते हो उनकी आवृत्तियों के बारे में?

~~ 11.23 दो तत्व A और B के देव ब्रॉगली तरंगदैर्घ्य $\lambda_1$ और $\lambda_2$ मिलाकर तत्व C द्वारा बनाया जाता है। प्रक्रिया प्राणी संरक्षण की देती है। तत्व C की देव ब्रॉगली तरंगदैर्घ्य ढूँढें। (गतिकीय है ।

~~ 11.24 $E$ उर्जा के न्यूट्रॉन बीम को $d=0.1 nm$ अंतराल वाली सतह पर प्रतिछाति होती है। प्रत्यक्ष बीम में अधिकतम प्रकाश $30^{\circ}$ पर होता है। बीम की क्षमता कितनी होती है $eV$ में?

LA

~~ 11.25 $10^{-2} m.$ वर्ग, $10^{-3} m$ मोटाई वाले एक पतला निशान (नायट्रियम) को सोड़िए, जो जब उस पर प्रकाशितता $100 W / m^{2}(\lambda=660 nm)$ का एक प्रकाश पड़ता है तो एक फोटोवोल्टाक उत्पन्न करता है। जब नायट्रियम पर एक फोटॉन टकराता है, तो एक फोटोइलेक्ट्रॉन उत्पन्न होने की संभावना ढूँढें। [$Na$ की घनत्वा लें $0.97 kg / m^{3}$].

~~ 11.26 एक धातुर पूर्व में एक इलेक्ट्रॉन को एक दूरी $d$ (एक अनंत सप्ताह) से फबेंगे। प्लेट द्वारा आकर्षण का बल $\frac{1}{4} \frac{q^{2}}{4 \pi \varepsilon_0 d^{2}}$ दिया जाता है

एक अनंतदूरी से चार्ज को लेने के लिए काम का आकलन करें। $d=0.1 nm$ लेते हुए, वर्कशॉप में काम जानिए इलेक्ट्रॉन वोल्ट में। [$d<0.1 nm$ के लिए ऐसा एक बल कानून मान्य नहीं है]।

11.27 एक छात्र प्रकाशवैद्युत प्रभाव पर एक प्रयोग करता है, उपयोग करता है दो तत्व A और B। $वी_{\text{रोक}} बनाम$ वायुमंडलीय वी का एक चित्र 11.2 में दिया गया है।

(ख) कौन सा तत्व A या $B$ का एक अधिक कार्य-कार्य लक्षण है?

(ii) एक परमाणु के विद्युत आवेश = 1.6 x $10^{-19}$ सी, चुंबकीय से निकाले $h$ का मान प्रायोगिकतानुसार पता करें, यह व A और B दोनों के लिए।

यह क्या कि आईन्स्टीन के सिद्धान्त के साथ मेल खाता है:

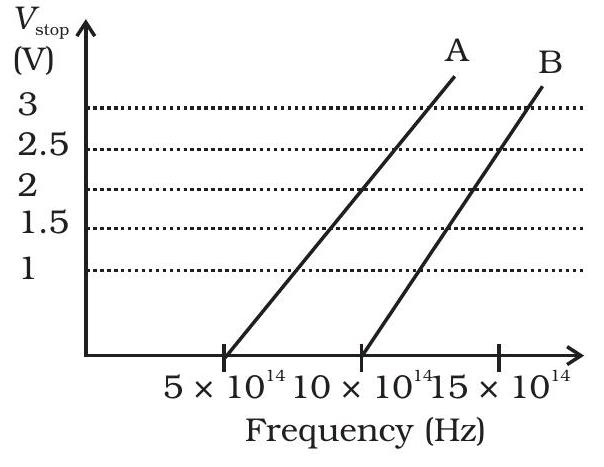Fig. 11.2

~~ 11.28 एक ही आयामी चलन के साथ चलने वाले एक चिंताविषयक A द्वारा B इंधन (भार्य) मार संशोधित । चिंताविषयक hai।

~~ 11.29 $20 डब्ल्यू$ बत्ती को $5000 \AA$ की तरंगदैर्शीक्षणत्मक उद्‌दीपन करते हुए और एक मद सतह को $2 मी$ दूर पर जगमगाती है। मान लें कि धातु पृष्ठ का कार्य लक्षण $2 ईवी$ है और धातु की सतह पर प्रति परमाणु वृत्त का इलाका था उसकी आयताकार परिधि का आयाम $1.5 A$।

(i) प्रति सेकंड बत्ती द्वारा निकाले जाने वाले फोटोन की गणना है । [कोई अन्य हानि मानें]

(ii) क्या फोटोइलेक्ट्रिक प्रकाशन होगी?

(iii) परमाणु वृत्त को कार्यलक्षण ( $2 ईवी$ ) के बराबर ऊर्जा प्राप्त करने में कितना समय लगेगा?

(iv) (iii) में गणना वाले समय-अवधि के भीतर परमाणु वृत्त को कितने फोटोन मानता है?

(v) क्या आप स्पष्ट कर सकते हैं कि प्रकाशवैद्युत प्रभाव कैसे तुरंत देखा गया था?

[संकेत: भाग (iii) में गणना का पारंपरिक विचार है और आप आगे ले सकते हैं उदाहरण के लिए एक लक्ष्य चुन सकते हैं, जैसे कि $1 सेमी$ का ऊर्जा कितने और कुछ होगा?]

अध्याय 11

~~ 11.1 (ड)

~~ 11.2 (ब)

~~ 11.3 (ड)

~~ 11.4 (सी)

~~ 11.5 (ब)

~~ 11.6 (अ)

~~ 11.7 (अ)

~~ 11.8 (सी)

~~ 11.9 (सी), (ड)

~~ 11.10 (अ), (सी)

~~ 11.11 (ब), (सी)

~~ 11.12 (अ), (ब), (सी)

~~ 11.13 (ब), (ड)

~~ 11.14 $ \quad \frac{\lambda_p}{\lambda_d}=\frac{p_x}{p_p}=\frac{\sqrt{2 m_{\alpha} E_{\alpha}}}{\sqrt{2 m_p E_p}}=\sqrt{8}:1$

~~ 11.15 (i) $ई_{\text{माध्यमरत्व}}=2 h v-\phi$

(ii) एक ही इलेक्ट्रॉन द्वारा 2 फोटोनों का आवेशन करने की संभावना बहुत कम होती है। इसलिए ऐसे प्रकाशन को ज्यादातर उपेक्षित किया जाएगा।

~~ 11.16 पहले मामले में दिए गए ऊर्जा दी गई ऊर्जा से कम है। दूसरे मामले में, माल को ऊर्जा प्रदान करनी होती है क्योंकि निकला फोटोन अधिक ऊर्जा वाला होता है। यह संतुलनशील पदार्थों के लिए संभव नहीं हो सकता।

~~ 11.17 जी नहीं, अधिक इलेक्ट्रॉन धातु के अंतर्गत बिखर जाते हैं। मेटल के सतह से बस कुछ निकलते हैं।

~~ 11.18 कुल $ई$ स्थिर रहता है

$न_1$ और $न_2$ एक्स-रे के फोटोनों और दृश्यमान क्षेत्र के फोटोनों की संख्या हो

$न_1 E_1=न_2 E_2$

$\frac{न_1}{न_2}=\frac{लैम्ब्डा_1}{\lambda_2}$

$\frac{न_1}{न_2}=\frac{1}{500}$।

11.19 धारा मेटल को साथ ले जाई जाती है। सूक्ष्मस्तर पर, परमाणु फोटन को अवशोषित करते हैं और उसकी गति मुख्य रूप से नाभि और इलेक्ट्रॉनों को संचारित होती है। उत्तेजित इलेक्ट्रॉन प्रकट होता है। गति के संरक्षण को नाभि और इलेक्ट्रॉनों को संचारित होने वाली गति के लिए ध्यान में रखना चाहिए।

~~ 11.20 अधिकतम ऊर्जा $=h v-\phi$

$(\frac{1230}{600}-\phi)=\frac{1}{2}(\frac{1230}{400}-\phi)$

$\phi=\frac{1230}{1200}=1.02 eV$.

~~ 11.21 $ \Delta x \Delta p \simeq \hbar$

$\Delta p \simeq \frac{\hbar}{\Delta x} \simeq \frac{1.05 \times 10^{-34} Js}{10^{-9} m}=1.05 \times 10^{-25}$

$E=\frac{p^{2}}{2 m}=\frac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31}}=\frac{1.05^{2}}{18.2} \times 10^{-19} J=\frac{1.05^{2}}{18.2 \times 1.6} eV$

$=3.8 \times 10^{-2} eV$

~~ 11.22 $ I=n_A n_A=n_B v_B$

$\frac{n_A}{n_B}=2=\frac{v_B}{v_A}$

बीम $B$ की आवृत्ति आवृत्ति $A$ की दो गुना होती है।

~~ 11.23

$p_c=|p_A|+|p_B|=\frac{h}{\lambda_A}+\frac{h}{\lambda_B}=\frac{h}{\lambda_c}=\frac{h}{\lambda_c}$ if $p_A, p_B>0$ or $p_A, p_B<0$

or $\lambda_c=\frac{\lambda_A \lambda_B}{\lambda_A+\lambda_B}$

यदि $p_A>0, p_B<0$ या $p_A<0, p_B>0$ है

$p_c=h \frac{\lambda_B-\lambda_A}{|\lambda_A \cdot \lambda_B|}=\frac{h}{\lambda_c}$

$\lambda_c=\frac{\lambda_B \cdot \lambda_A}{|\lambda_A-\lambda_B|}$.

~~ 11.24 $2 d \sin \theta=\lambda=d=10^{-10} m$.

$ \begin{gathered} p=\frac{h}{10^{-10}}=\frac{6.6 \times 10^{-34}}{10^{-10}}=6.6 \times 10^{-21} kg m / s \\ E=\frac{(6.6 \times 10^{-24})^{2}}{2 \times(1.7 \times 10^{-27})} \times 1.6 \times 10^{-19}=\frac{6.6^{2}}{2 \times 1.7} \times 1.6 \times 10^{-2} eV \\ =20.5 \times 10^{-2} eV=0.21 eV \end{gathered} $

~~ 11.25 $6 \times 10^{26} Na$ परमाणु वजन $23 kg$ माना जाता है।

लक्ष्य का आयतन $=(10^{-4} \times 10^{-3})=10^{-7} m^{3}$

सोडियम का घनत्व $=(d)=0.97 kg / m^{3}$

$6 \times 10^{26} Na$ परमाणुओं का आयतन $=\frac{23}{0.97} m^{3}=23.7 m^{3}$

$1 Na$ परमाणु द्वारा अवरुद्ध किया गया आयतन $=\frac{23}{0.97 \times 6 \times 10^{26}} m^{3}=3.95 \times 10^{-26} m^{3}$

लक्ष्य में सोडियम परमाणुओं की संख्या $=\frac{10^{-7}}{3.95 \times 10^{-26}}=2.53 \times 10^{18}$

बीम के लिए फोटन/सेकंड में $10^{-4} m^{2}=n$

प्रति सेकंड की ऊर्जा $n h v=10^{-4} J \times 100=10^{-2} W$

$h v($ ऑँकर $\lambda=660 nm)$ के लिए

$\frac{1234.5}{600}$

$ =2.05 eV=2.05 \times 1.6 \times 10^{-19}=3.28 \times 10^{-19} J $

$n=\frac{10^{-2}}{3.28 \times 10^{-19}}=3.05 \times 10^{16} / s$

$n=\frac{1}{3.2} \times 10^{17}=3.1 \times 10^{16}$

यदि $P$ थ्रून की संभावना है प्रति परमाणु, प्रति फोटन, प्रति सेकंड प्रकट हुए फोटोइलेक्ट्रॉनों की संख्या

$=P \times 3.1 \times 10^{16} \times 2.53 \times 10^{18}$

धारा $=P \times 3.1 \times 10^{+16} \times 2.53 \times 10^{18} \times 1.6 \times 10^{-19} A$

$ =P \times 1.25 \times 10^{+16} A $

इसे $100 \mu A$ के बराबर होना चाहिए या

$P=\frac{100 \times 10^{-6}}{1.25 \times 10^{+16}}$

$\therefore P=8 \times 10^{-21}$

इस तरह से एक एकल फोटॉन द्वारा एक एकल परमाणु पर फोटमिशन की संभावना 1 से बहुत कम होती है। (इसीलिए एक परमाणु द्वारा दो फोटॉन का संशोधन अनर्थक होता है)।

~~ 11.26 बाहरी एजेंसी द्वारा किया जाने वाला कार्य $=+\frac{1}{4 \pi \varepsilon_0} \cdot \frac{1}{4} \int_d^{\infty} \frac{q^{2}}{x^{2}} d x=\frac{1}{4} \cdot \frac{q^{2}}{4 \pi \varepsilon_0 d}$

$d=0.1 \text{ नैनोमीटर}$ के साथ, ऊर्जा $=\frac{(1.6 \times 10^{-19}) \times 9 \times 10^{9}}{4(10^{-10}) \times 1.6 \times 10^{-19}} \text{ इलेक्ट्रॉन-वोल्ट}$

$=\frac{1.6 \times 9}{4} \text{ इलेक्ट्रॉन-वोल्ट}=3.6 \text{ इलेक्ट्रॉन-वोल्ट}$ ~~ 11.27 (i) बी के लिए अधिक आवरण तान के रूप में $0$ हिटाने की तत्परता। इसलिए इसमें अधिक कार्य-लोचन होता है।

(ii) A के लिए ढलान $\frac{h}{e}=\frac{2}{(10-5) \times 10^{14}}$।

$\frac{2.5}{(15-10) \times 10^{14}}$ बी के लिए।

$h= \frac{1.6 \times 10^{-19}}{5} \times 2 \times 10^{-14}=6.04 \times 10^{-34} , जूल-सेकंड$, A के लिए। $=\frac{1.6 \times 10^{-19} \times 2.5 \times 10^{-14}}{5}=8 \times 10^{-34} , जूल-सेकंड$, B के लिए।

क्योंकि $h$ अलग-अलग है, इसलिए प्रयोग सिद्धांत के साथ मेल नहीं खट्‌टा है।

~~ 11.28

$म_Aव=म_Aव_1+म_Bव_2$

$\frac{1}{2} म_Aव^{2}=\frac{1}{2} म_Aव_1^{2}+\frac{1}{2} म_Bव_2^{2}$

$\therefore \frac{1}{2} म_A(व-व_1)(व_A+व_1)=\frac{1}{2} म_Bव_B^{2}$

$\therefore व+व_1=व_2$

या $व=व_2-व_1$

$\therefore व_1=(\frac{म_A-म_B}{म_A+म_B}) व, \quad$ और $\quad व_2=(\frac{2 म_A}{म_A+म_B}) व$

$\therefore \lambda _{\text{प्रारंभिक }}=\frac{h}{म_A व}$

$\lambda _{\text{अंतिम }}=\frac{h}{म_A व}=|\frac{h(म_A+म_B)}{म_A(म_A-म_B) व}|$

$\therefore \Delta \lambda=\frac{h}{म_A व}[|\frac{.म_A+म_B)}{म_A-म_B}|-1]$

~~ 11.29 (i) $\frac{d N}{d t}=\frac{P}{(h c / \lambda)}=5 \times 10^{19} / s$

(ii) $\frac{h c}{\lambda}=2.49 इलेक्ट्रॉन-वोल्ट>वर्क फ़ंक्शन (W_0):$ हाँ।

(iii) P. $\frac{\pi r^{2}}{4 \pi d^{2}} \Delta t=W_0, \Delta t=28.4 s$

(iv) $N=(\frac{d N}{d t}) \times \frac{\pi r^{2}}{4 \pi d^{2}} \times \Delta t=2$