4.1 भूमिका

पिछली कक्षाओं में, आप एक चर वाले रैखिक समीकरणों का अध्ययन कर चुके हैं। क्या आप एक चर वाला कोई रैखिक समीकरण लिख सकते हैं? आप कह सकते हैं कि $x+1=0, x+\sqrt{2}=0$ और $\sqrt{2} y+\sqrt{3}=0$ एक चर वाले रैखिक समीकरणों के उदाहरण हैं। आप यह भी जानते हैं कि ऐसे समीकरणों का एक अद्वितीय (अर्थात् एक और केवल एक) हल होता है। आपको संभवतः यह भी याद होगा कि एक संख्या रेखा पर हल को किस प्रकार निरूपित किया जाता है। इस अध्याय में, हम एक चर वाले रैखिक समीकरणों पर पुनः विचार करेंगे और उनसे संबंधित ज्ञान को दो चरों वाले रैखिक समीकरणों पर लागू करेंगे। यहाँ हम इस प्रकार के प्रश्नों पर विचार करेंगे: क्या दो चरों वाले रैखिक समीकरण का एक हल होता है? यदि हाँ, तो क्या यह अद्वितीय होता है? कार्तीय तल पर हल किस प्रकार दिखाई पड़ता है? इस प्रकार के प्रश्नों का अध्ययन करने के लिए, हम अध्याय 3 में बताई गई संकल्पनाओं का भी प्रयोग करेंगे।

4.2 रैखिक समीकरण

आइए पहले हम यह देखें कि अभी तक आपने क्या-क्या अध्ययन किया है। आइए हम निम्नलिखित समीकरण लें :

$$ 2 x+5=0 $$

इसका हल, अर्थात् समीकरण का मूल $-\frac{5}{2}$ है। इसे संख्या रेखा पर इस प्रकार निरूपित किया जा सकता है, जैसा कि नीचे की आकृति में दिखाया गया है :

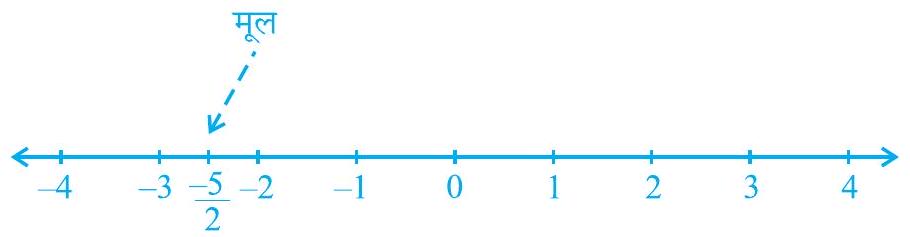
आकृति 4.1

एक समीकरण को हल करते समय निम्नलिखित बातों को ध्यान में रखना होता है।

एक रैखिक समीकरण पर तब कोई प्रभाव नहीं पड़ता जबकि:

(i) समीकरण के दोनों पक्षों में समान संख्या जोड़ी या घटाई जाती है।

(ii) समीकरण के दोनों पक्षों को समान शून्येतर संख्या से गुणा या भाग दिया जाता है। आइए अब हम निम्नलिखित स्थिति पर विचार करें:

नागपुर में भारत और श्रीलंका के बीच खेले गए एक एकदिवसीय अंतर्राष्ट्रीय क्रिकेट मैच में दो भारतीय बल्लेबाजों ने एक साथ मिलकर 176 रन बनाए। इस जानकारी को एक समीकरण के रूप में व्यक्त कीजिए।

यहाँ आप यह देख सकते हैं कि दोनों बल्लेबाजों में से किसी भी बल्लेबाज द्वारा बनाए गए रन ज्ञात नहीं हैं, अर्थात् यहाँ दो अज्ञात राशियाँ हैं। आइए हम इन अज्ञात राशियों को $x$ और $y$ से प्रकट करें। इस तरह एक बल्लेबाज द्वारा बनाए गए रनों की संख्या $x$ है और दूसरे बल्लेबाज द्वारा बनाए गए रनों की संख्या $y$ है। हम जानते हैं कि

$$ x+y=176 $$

है, जो कि अभीष्ट समीकरण है।

यह दो चरों वाले एक रैखिक समीकरण का एक उदाहरण है। यह परंपरा रही है कि इस प्रकार के समीकरणों के चरों को $x$ और $y$ से प्रकट किया जाता है, परंतु अन्य अक्षरों का भी प्रयोग किया जा सकता है। दो चरों वाले रैखिक समीकरणों के कुछ उदाहरण ये हैं:

$$ 1.2 s+3 t=5, p+4 q=7, \pi u+5 v=9 \text { और } 3=\sqrt{2} x-7 y $$

क्या आप कुछ और उदाहरण दे सकते हैं? ध्यान दीजिए कि आप इन समीकरणों को क्रमश: $1.2 s+3 t-5=0, p+4 q-7=0, \pi u+5 v-9=0$ और $\sqrt{2} x-7 y-3=0$ के रूप में व्यक्त कर सकते हैं।

अतः उस समीकरण को, जिसे $a x+b y+c=0$ के रूप में व्यक्त किया जा सकता हो, जहाँ $a, b$ और $c$ वास्तविक संख्याएँ हैं और $a$ और $b$ दोनों शून्य नहीं हैं, दो चरों वाला रैखिक समीकरण (linear equation in two variables) कहा जाता है।

4.3 रैखिक समीकरण का हल

आपने देखा है कि एक चर वाले प्रत्येक रैखिक समीकरण का एक अद्वितीय हल होता है। दो चरों वाले रैखिक समीकरण के हल के बारे में आप क्या कह सकते हैं? क्योंकि समीकरण में दो चर हैं, इसलिए हल का अर्थ होता है $x$ तथा $y$ के उन मानों का युग्म जो दिए हुए समीकरण को संतुष्ट करते हैं। आइए, हम समीकरण $2 x+3 y=12$ लें। यहाँ $x=3$ और $y=2$ एक हल है, क्योंकि जब हम ऊपर के समीकरण में $x=3$ और $y=2$ प्रतिस्थापित करते हैं तब हमें यह प्राप्त होता है:

$$ 2 x+3 y=(2 \times 3)+(3 \times 2)=12 $$

इस हल को एक क्रमित युग्म $(3,2)$ के रूप में लिखा जाता है, जिसमें पहले $x$ का और उसके बाद $y$ का मान लिखा जाता है। इसी प्रकार, $(0,4)$ भी ऊपर दिए गए समीकरण का एक हल है।

इसके विपरीत, $(1,4)$ ऊपर दिए गए समीकरण का एक हल नहीं है, क्योंकि $x=1$ और $y=4$ प्रतिस्थापित करने पर हमें $2 x+3 y=14$ प्राप्त होता है जो 12 नहीं है। ध्यान दीजिए कि $(0,4)$ तो एक हल है परंतु $(4,0)$ एक हल नहीं है। इस तरह आपने $2 x+3 y=12$ के कम से कम दो हल $(3,2)$ और $(0,4)$ प्राप्त कर लिए हैं।

क्या आप कोई अन्य हल प्राप्त कर सकते हैं? क्या आप इस बात से सहमत हैं कि $(6,0)$ एक अन्य हल है? यदि हाँ, तो आप इसे सत्यापित कीजिए। वस्तुतः निम्न विधि से हम कई हल प्राप्त कर सकते हैं:

आप $2 x+3 y=12$ में अपनी इच्छानुसार $x$ का एक मान (मान लीजिए $x=2$ ) ले सकते हैं। तब समीकरण $4+3 y=12$ हो जाता है, जो कि एक चर वाला रैखिक समीकरण

है। इसे हल करने पर हमें $y=\frac{8}{3}$ प्राप्त होता है। अतः $\left(2, \frac{8}{3}\right), 2 x+3 y=12$ का एक अन्य हल है। इसी प्रकार, $x=-5$ लेने पर हम पाते हैं कि समीकरण $-10+3 y=12$ हो जाता है। इससे $y=\frac{22}{3}$ प्राप्त होता है। अतः $\left(-5, \frac{22}{3}\right), 2 x+3 y=12$ का एक अन्य हल है। इसलिए दो चरों वाले रैखिक समीकरण के विभिन्न हलों का कोई अंत नहीं है। कहने का अर्थ है कि दो चरों वाले रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं।

4.4 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. $a x+b y+c=0$ के रूप के समीकरण को जहाँ, $a, b$ और $c$ वास्तविक संख्याएँ हैं और $a$ और $b$ दोनों शून्य नहीं हैं, दो चरों वाला रैखिक समीकरण कहा जाता है।

2. दो चरों वाले रैखिक समीकरण के अपरिमित रूप से अनेक हल होते हैं।

3. दो चरों वाले रैखिक समीकरण के आलेख पर स्थित प्रत्येक बिंदु रैखिक समीकरण का एक हल होता है। साथ ही, रैखिक समीकरण का प्रत्येक हल रैखिक समीकरण के आलेख पर स्थित एक बिंदु होता है।