6.1 भूमिका

अध्याय 5 में, आप पढ़ चुके हैं कि एक रेखा को खींचने के लिए न्यूनतम दो बिंदुओं की आवश्यकता होती है। आपने कुछ अभिगृहीतों (axioms) का भी अध्ययन किया है और उनकी सहायता से कुछ अन्य कथनों को सिद्ध किया है। इस अध्याय में, आप कोणों के उन गुणों का अध्ययन करेंगे जब दो रेखाएँ परस्पर प्रतिच्छेद करती हैं और कोणों के उन गुणों का भी अध्ययन करेंगे जब एक रेखा दो या अधिक समांतर रेखाओं को भिन्न-भिन्न बिंदुओं पर काटती है। साथ ही, आप इन गुणों का निगमनिक तर्कण (deductive reasoning) द्वारा कुछ कथनों को सिद्ध करने में भी प्रयोग करेंगे (देखिए परिशिष्ट 1)। आप पिछली कक्षाओं में इन कथनों की कुछ क्रियाकलापों द्वारा जाँच (पुष्टि) कर चुके हैं।

आप अपने दैनिक जीवन में समतल पृष्ठों के किनारों (edges) के बीच बने अनेक प्रकार के कोण देखते हैं। समतल पृष्ठों का प्रयोग करके, एक ही प्रकार के मॉडल बनाने के लिए, आपको कोणों के बारे में विस्तृत जानकारी की आवश्यकता होती है। उदाहरणार्थ, आप अपने विद्यालय की प्रदर्शिनी के लिए बाँसों का प्रयोग करके एक झोंपड़ी का मॉडल बनाना चाहते हैं। सोचिए, आप इसे कैसे बनाएँगे। कुछ बाँसों को आप परस्पर समांतर रखेंगे और कुछ को तिरछा रखेंगे। जब एक आर्किटेक्ट (architect) एक बहुतलीय भवन के लिए एक रेखाचित्र खींचता है, तो उसे विभिन्न कोणों पर प्रतिच्छेदी और समांतर रेखाएँ खींचनी पड़ती हैं। क्या आप सोचते हैं कि वह रेखाओं और कोणों के ज्ञान के बिना इस भवन की रूपरेखा खींच सकता है?

विज्ञान में, आप प्रकाश के गुणों का किरण आरेख (ray diagrams) खींच कर अध्ययन करते हैं। उदाहरणार्थ, प्रकाश के अपवर्तन (refraction) गुण का अध्ययन करने के लिए, जब

प्रकाश की किरणें एक माध्यम (medium) से दूसरे माध्यम में प्रवेश करती हैं, आप प्रतिच्छेदी रेखाओं और समांतर रेखाओं के गुणों का प्रयोग करते हैं। जब एक पिंड पर दो या अधिक बल कार्य कर रहे हों, तो आप इन बलों का उस पिंड पर परिणामी बल ज्ञात करने के लिए, एक ऐसा आरेख खींचते हैं जिसमें बलों को दिष्ट रेखाखंडों (directed line segments) द्वारा निरूपित किया जाता है। उस समय, आपको उन कोणों के बीच संबंध जानने की आवश्यकता होगी जिनकी किरणें (अथवा रेखाखंड) परस्पर समांतर या प्रतिच्छेदी होंगी। एक मीनार की ऊँचाई ज्ञात करने अथवा किसी जहाज की एक प्रकाश पुंज (light house) से दूरी ज्ञात करने के लिए, हमें क्षैतिज और दृष्टि रेखा (line of sight) के बीच बने कोण की जानकारी की आवश्यकता होगी। प्रचुर मात्रा में ऐसे उदाहरण दिए जा सकते हैं जहाँ रेखाओं और कोणों का प्रयोग किया जाता है। ज्यामिति के आने वाले अध्यायों में, आप रेखाओं और कोणों के इन गुणों का अन्य उपयोगी गुणों को निगमित (निकालने) करने में प्रयोग करेंगे।

आइए पहले हम पिछली कक्षाओं में रेखाओं और कोणों से संबंधित पढ़े गए पदों और परिभाषाओं का पुनर्विलोकन करें।

6.2 आधारभूत पद और परिभाषाएँ

याद कीजिए कि एक रेखा का वह भाग जिसके दो अंत बिंदु हों एक रेखाखंड कहलाता है और रेखा का वह भाग जिसका एक अंत बिंदु हो एक किरण कहलाता है। ध्यान दीजिए कि रेखाखंड $\mathrm{AB}$ को $\overline{\mathrm{AB}}$ से व्यक्त किया जाता है और उसकी लंबाई को $\mathrm{AB}$ से व्यक्त किया जाता है। किरण $\mathrm{AB}$ को $\overrightarrow{\mathrm{AB}}$ से और रेखा $\mathrm{AB}$ को $\overleftrightarrow{\mathrm{AB}}$ से व्यक्त किया जाता है। परन्तु हम इन संकेतनों का प्रयोग नहीं करेंगे तथा रेखा $\mathrm{AB}$, किरण $\mathrm{AB}$, रेखाखंड $\mathrm{AB}$ और उसकी लंबाई को एक ही संकेत $\mathrm{AB}$ से व्यक्त करेंगे। इनका अर्थ संदर्भ से स्पष्ट हो जाएगा। कभी-कभी छोटे अक्षर जैसे $l, m, n$ इत्यादि का प्रयोग रेखाओं को व्यक्त करने में किया जाएगा।

यदि तीन या अधिक बिंदु एक ही रेखा पर स्थित हों, तो वे संरेख बिंदु (collinear points) कहलाते हैं, अन्यथा वे असंरेख बिंदु (non-collinear points) कहलाते हैं।

याद कीजिए कि जब दो किरणें एक ही अंत बिंदु से प्रारम्भ होती हैं, तो एक कोण (angle) बनता है। कोण को बनाने वाली दोनों किरणें कोण की भुजाएँ (arms या sides) कहलाती हैं और वह उभयनिष्ठ अंत बिंदु कोण का शीर्ष (vertex) कहलाता है। आप पिछली कक्षाओं में, विभिन्न प्रकार के कोणों जैसे न्यून कोण (acute angle), समकोण (right angle), अधिक कोण (obtuse angle), ॠजु कोण (straight angle) और प्रतिवर्ती कोण (reflex angle) के बारे में पढ़ चुके हैं (देखिए आकृति 6.1)।

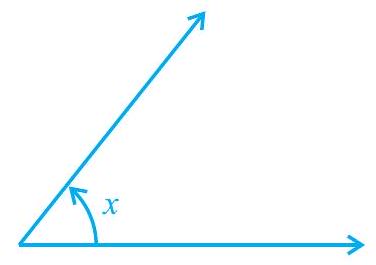
(i) न्यून कोण : $0^{\circ}<x<90^{\circ}$

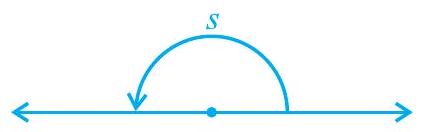
(iv) ऋजु कोण : $s=180^{\circ}$

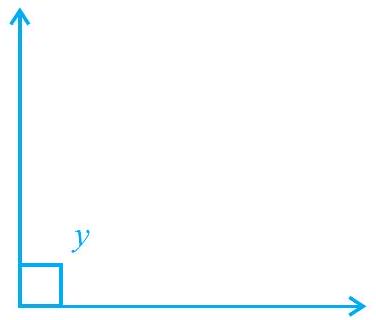
(ii) समकोण : $y=90^{\circ}$

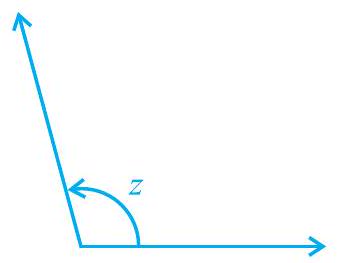
(iii) अधिक कोण : $90^{\circ}<z<180^{\circ}$

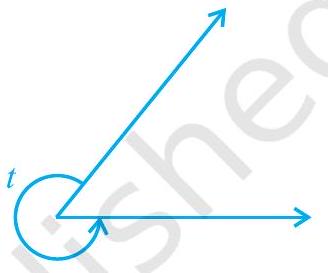
(v) प्रतिवर्ती कोण : $180^{\circ}<t<360^{\circ}$

आकृति 6.1 : कोणों के प्रकार

एक न्यून कोण का माप $0^{\circ}$ और $90^{\circ}$ के बीच होता है, जबकि एक समकोण का माप ठीक $90^{\circ}$ होता है। $90^{\circ}$ से अधिक परन्तु $180^{\circ}$ से कम माप वाला कोण अधिक कोण कहलाता है। साथ ही, याद कीजिए कि एक ऋजु कोण $180^{\circ}$ के बराबर होता है। वह कोण जो $180^{\circ}$ से अधिक, परन्तु $360^{\circ}$ से कम माप का होता है एक प्रतिवर्ती कोण कहलाता है। इसके अतिरिक्त, यदि दो कोणों का योग एक समकोण के बराबर हो, तो ऐसे कोण पूरक कोण (complementary angles) कहलाते हैं और वे दो कोण, जिनका योग $180^{\circ}$ हो, संपूरक कोण (supplementary angles) कहलाते हैं।

आप पिछली कक्षाओं में आसन्न कोणों (adjacent angles) के बारे में भी पढ़ चुके हैं (देखिए आकृति 6.2)। दो कोण आसन्न कोण (adjacent angles) कहलाते हैं, यदि उनमें एक उभयनिष्ठ शीर्ष हो, एक उभयनिष्ठ भुजा हो और उनकी वे भुजाएँ जो उभयनिष्ठ नहीं हैं, उभयनिष्ठ भुजा के विपरीत ओर स्थित हों। आकृति 6.2 में, $\angle \mathrm{ABD}$ और $\angle \mathrm{DBC}$ आसन्न कोण हैं। किरण $\mathrm{BD}$ इनकी उभयनिष्ठ भुजा है और $\mathrm{B}$ इनका उभयनिष्ठ

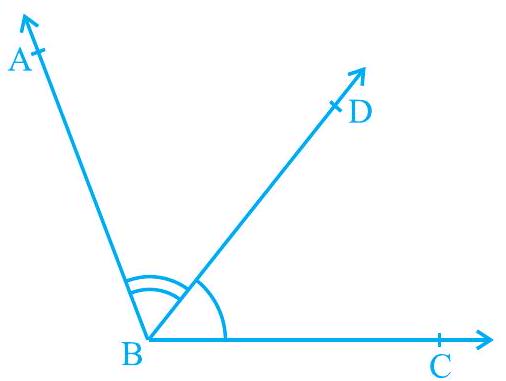
आकृति 6.2 : आसन्न कोण

शीर्ष है। किरण $\mathrm{BA}$ और किरण $\mathrm{BC}$ वे भुजाएँ हैं जो उभयनिष्ठ नहीं हैं। इसके अतिरिक्त, जब दो कोण आसन्न कोण होते हैं, तो उनका योग उस कोण के बराबर होता है जो इनकी उन भुजाओं से बनता है, जो उभयनिष्ठ नहीं हैं। अतः हम लिख सकते हैं कि $\angle \mathrm{ABC}=\angle \mathrm{ABD}+\angle \mathrm{DBC}$ है।

ध्यान दीजिए कि $\angle \mathrm{ABC}$ और $\angle \mathrm{ABD}$ आसन्न कोण नहीं हैं। क्यों? इसका कारण यह है कि अउभयनिष्ठ भुजाएँ (अर्थात् वे भुजाएँ जो उभयनिष्ठ नहीं हैं) $\mathrm{BD}$ और $\mathrm{BC}$ उभयनिष्ठ भुजा $\mathrm{BA}$ के एक ही ओर स्थित है।

यदि आकृति 6.2 में, अउभयनिष्ठ भुजाएँ $\mathrm{BA}$ और $\mathrm{BC}$ एक रेखा बनाएँ, तो यह आकृति 6.3 जैसा

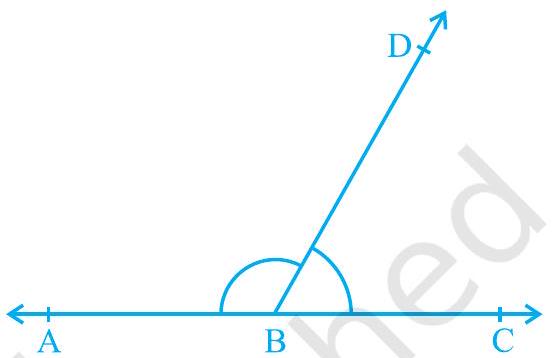
आकृति 6.3 : कोणों का रैखिक युग्म लगेगा। इस स्थिति में, $\angle \mathrm{ABD}$ और $\angle \mathrm{DBC}$ कोणों का एक रैखिक युग्म (linear pair of angles) बनाते हैं।

आप शीर्षाभिमुख कोणों (vertically opposite angles) को भी याद कर सकते हैं, जो दो रेखाओं, मान लीजिए, $\mathrm{AB}$ और $\mathrm{CD}$ को परस्पर बिंदु $\mathrm{O}$ पर प्रतिच्छेद करने पर बनते हैं (देखिए आकृति 6.4)। यहाँ शीर्षाभिमुख कोणों के दो युग्म हैं। इनमें से एक

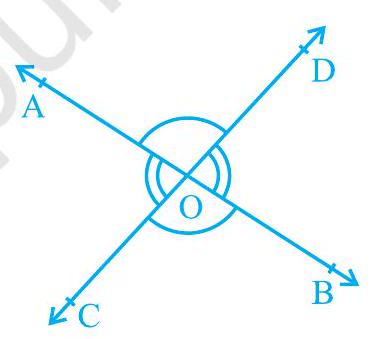
आकृति 6.4 : शीर्षाभिमुख कोण युग्म $\angle \mathrm{AOD}$ और $\angle \mathrm{BOC}$ का है। क्या आप दूसरा युग्म ज्ञात कर सकते हैं?

6.3 प्रतिच्छेदी रेखाएँ और अप्रतिच्छेदी रेखाएँ

एक कागज़ पर दो भिन्न रेखाएँ $\mathrm{PQ}$ और $\mathrm{RS}$ खींचिए। आप देखेंगे कि आप इन रेखाओं को दो प्रकार से खींच सकते हैं, जैसा कि आकृति 6.5 (i) और आकृति 6.5 (ii) में दर्शाया गया है।

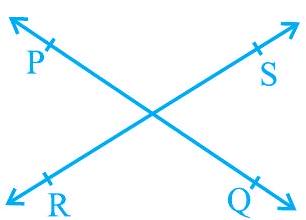
(i) प्रतिच्छेदी रेखाएँ

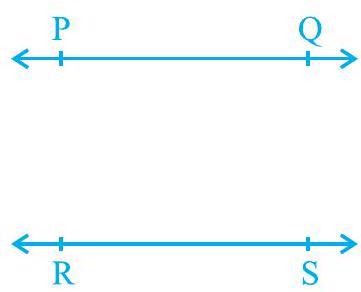
(ii) अप्रतिच्छेदी (समांतर) रेखाएँ

आकृति 6.5 : दो रेखाएँ खींचने के विभिन्न प्रकार

रेखा की इस अवधारणा को भी याद कीजिए कि वह दोनों दिशाओं में अनिश्चित रूप से विस्तृत होती है। रेखाएँ $\mathrm{PQ}$ और $\mathrm{RS}$ आकृति 6.5 (i) में प्रतिच्छेदी रेखाएँ हैं और आकृति 6.5 (ii) में ये समांतर रेखाएँ हैं। ध्यान दीजिए कि इन दोनों समांतर रेखाओं के विभिन्न बिंदुओं पर उनके उभयनिष्ठ लम्बों की लंबाइयाँ समान रहेंगी। यह समान लंबाई दोनों समांतर रेखाओं के बीच की दूरी कहलाती है।

6.4 कोणों के युग्म

अनुच्छेद 6.2 में, आप कोणों के कुछ युग्मों जैसे पूरक कोण, संपूरक कोण, आसन्न कोण, कोणों का रैखिक युग्म, इत्यादि की परिभाषाओं के बारे में पढ़ चुके हैं। क्या आप इन कोणों में किसी संबंध के बारे में सोच सकते हैं? आइए अब उन कोणों में संबंध पर विचार करें जिन्हें कोई किरण किसी रेखा पर स्थित होकर बनाती है, जैसा कि आकृति 6.6 में दर्शाया गया है। रेखा को $\mathrm{AB}$ और किरण को $\mathrm{OC}$ कहिए। बिंदु $\mathrm{O}$ पर बनने वाले कोण क्या हैं? ये

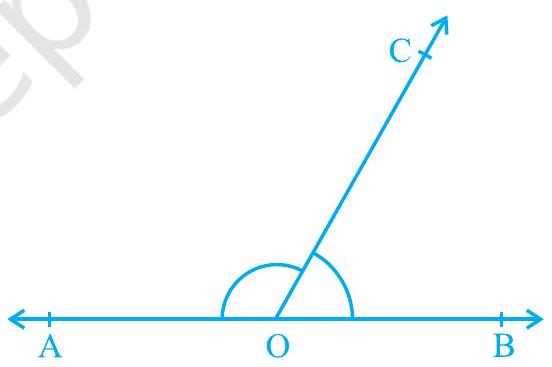
आकृति 6.6 : कोणों का रैखिक युग्म $\angle \mathrm{AOC}, \angle \mathrm{BOC}$ और $\angle \mathrm{AOB}$ हैं।

क्या हम $\angle \mathrm{AOC}+\angle \mathrm{BOC}=\angle \mathrm{AOB}$ लिख सकते हैं?

हाँ! (क्यों? अनुच्छेद 6.2 में दिए आसन्न कोणों को देखिए।)

$\angle \mathrm{AOB}$ का माप क्या है? यह $180^{\circ}$ है। (क्यों?)

क्या (1) ओर (2) से, आप कह सकते हैं कि $\angle \mathrm{AOC}+\angle \mathrm{BOC}=180^{\circ}$ है? हाँ! (क्यों?) उपरोक्त चर्चा के आधार पर, हम निम्न अभिगृहीत को लिख सकते हैं:

अभिगृहीत 6.1 : यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग $180^{\circ}$ होता है।

याद कीजिए कि जब दो आसन्न कोणों का योग $180^{\circ}$ हो, तो वे कोणों का एक रैखिक युग्म बनाते हैं।

अभिगृहीत 6.1 में यह दिया है कि ‘एक किरण एक रेखा पर खड़ी हो’। इस दिए हुए से, हमने निष्कर्ष निकाला कि इस प्रकार बने दोनों आसन्न कोणों का योग $180^{\circ}$ होता है। क्या हम अभिगृहीत 6.1 को एक विपरीत प्रकार से लिख सकते हैं? अर्थात् अभिगृहीत 6.1 के निष्कर्ष को दिया हुआ मानें और उसके दिए हुए को निष्कर्ष मानें। तब हमें यह प्राप्त होगा:

(A) यदि दो आसन्न कोणों का योग $180^{\circ}$ है, तो एक किरण एक रेखा पर खड़ी होती है (अर्थात् अउभयनिष्ठ भुजाएँ एक ही रेखा में हैं)।

अब आप देखते हैं कि अभिगृहीत 6.1 और कथन (A) एक दूसरे के विपरीत हैं। हम इनमें से प्रत्येक को दूसरे का विलोम (converse) कहते हैं। हम यह नहीं जानते कि कथन (A) सत्य है या नहीं। आइए इसकी जाँच करें। विभिन्न मापों के, आकृति 6.7 में दर्शाए अनुसार, आसन्न कोण खींचिए। प्रत्येक स्थिति में, अउभयनिष्ठ भुजाओं में से एक भुजा के अनुदिश एक पटरी (ruler) रखिए। क्या दूसरी भुजा भी इस पटरी के अनुदिश स्थित है?

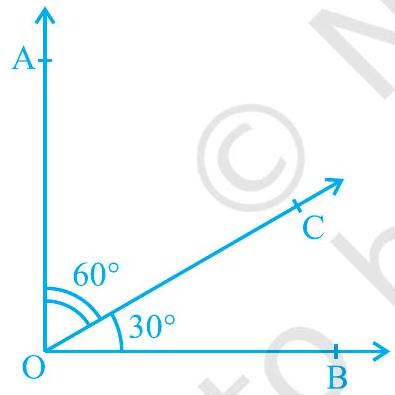
(i)

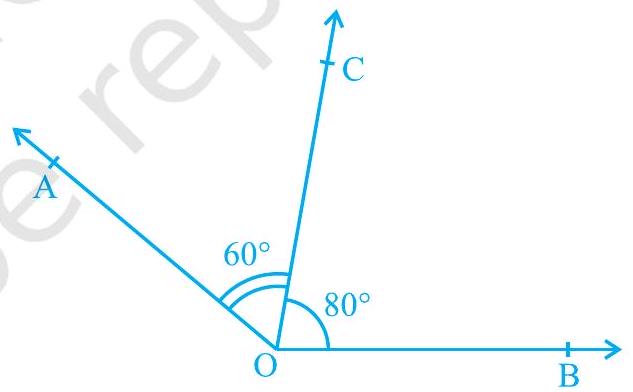
(ii)

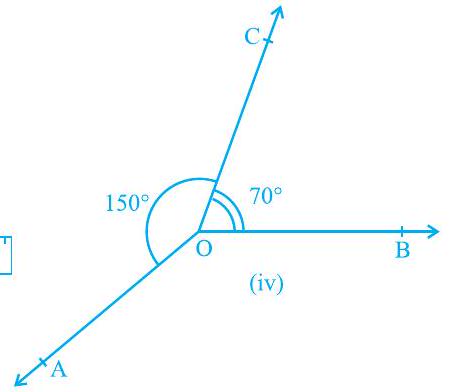
आकृति 6.7 : विभिन्न मापों के आसन्न कोण

आप पाएँगे कि केवल आकृति 6.7 (iii) में ही दोनों अउभयनिष्ठ भुजाएँ पटरी के अनुदिश हैं, अर्थात् $\mathrm{A}, \mathrm{O}$ और $\mathrm{B}$ एक ही रेखा पर स्थित हैं और किरण $\mathrm{OC}$ इस रेखा पर खड़ी है। साथ ही, यह भी देखिए कि $\angle \mathrm{AOC}+\angle \mathrm{COB}=125^{\circ}+55^{\circ}=180^{\circ}$ है। इससे आप निष्कर्ष निकाल सकते हैं कि कथन (A) सत्य है। अतः, आप इसे एक अभिगृहीत के रूप में निम्न प्रकार लिख सकते हैं :

अभिगृहीत 6.2 : यदि दो आसन्न कोणों का योग $180^{\circ}$ है, तो उनकी अउभयनिष्ठ भुजाएँ एक रेखा बनाती हैं।

स्पष्ट कारणों से, उपरोक्त दोनों अभिगृहीतों को मिला कर रैखिक युग्म अभिगृहीत (Linear Pair Axiom) कहते हैं।

आइए अब उस स्थिति की जाँच करें जब दो रेखाएँ प्रतिच्छेद करती हैं।

पिछली कक्षाओं से आपको याद होगा कि यदि दो रेखाएँ परस्पर प्रतिच्छेद करें, तो शीर्षाभिमुख कोण बराबर होते हैं। आइए अब इस परिणाम को सिद्ध करें। एक उपपत्ति (proof) में निहित अवयवों के लिए, परिशिष्ट 1 को देखिए और नीचे दी हुई उपपत्ति को पढ़ते समय इन्हें ध्यान में रखिए।

प्रमेय 6.1 : यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं। उपपत्ति : उपरोक्त कथन में यह दिया है कि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं। अतः मान लीजिए कि $\mathrm{AB}$ और $\mathrm{CD}$ दो रेखाएँ हैं जो परस्पर बिंदु $\mathrm{O}$ पर प्रतिच्छेद करती हैं, जैसा कि आकृति 6.8 में दर्शाया गया है। इससे हमें शीर्षाभिमुख कोणों के निम्न दो युग्म प्राप्त होते हैं:

(i) $\angle \mathrm{AOC}$ और $\angle \mathrm{BOD}$ (ii) $\angle \mathrm{AOD}$ और $\angle \mathrm{BOC}$

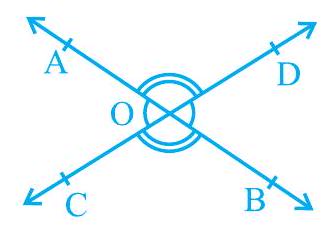
आकृति 6.8 : शीर्षाभिमुख कोण हमें सिद्ध करना है कि $\angle \mathrm{AOC}=\angle \mathrm{BOD}$ है और $\angle \mathrm{AOD}=\angle \mathrm{BOC}$ है। अब किरण $\mathrm{OA}$ रेखा $\mathrm{CD}$ पर खड़ी है।

अत: $\angle \mathrm{AOC}+\angle \mathrm{AOD}=180^{\circ}$

क्या हम $\angle \mathrm{AOD}+\angle \mathrm{BOD}=180^{\circ}$ लिख सकते हैं? हाँ। (क्यों?)

(1) और (2) से, हम लिख सकते हैं कि:

$$ \angle \mathrm{AOC}+\angle \mathrm{AOD}=\angle \mathrm{AOD}+\angle \mathrm{BOD} $$

इससे निष्कर्ष निकलता है कि $\angle \mathrm{AOC}=\angle \mathrm{BOD}$ (अनुच्छेद 5.2 का अभिगृहीत 3 देखिए)

इसी प्रकार, सिद्ध किया जा सकता है कि $\angle \mathrm{AOD}=\angle \mathrm{BOC}$ है।

आइए अब रैखिक युग्म अभिगृहीत और प्रमेय 6.1 पर आधारित कुछ उदाहरण हल करें।

टिप्पणी: उपरोक्त गुण को दो से अधिक रेखाओं के लिए भी लागू किया जा सकता है। आइए अब समांतर रेखाओं से संबंधित कुछ प्रश्न हल करें:

6.6 सारांश

इस अध्याय में, आपने निम्न बिंदुओं का अध्ययन किया है:

1. यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दोनों आसन्न कोणों का योग $180^{\circ}$ होता है और विलोमतः यदि दो आसन्न कोणों का योग $180^{\circ}$ है, तो उनकी अउभयनिष्ठ भुजाएँ एक रेखा बनाती हैं। इन गुणों को मिलाकर रैखिक युग्म अभिगृहीत कहते हैं।

2. यदि दो रेखाएँ परस्पर प्रतिच्छेद करें, तो शीर्षाभिमुख कोण बराबर होते हैं।

3. वे रेखाएँ जो एक ही रेखा के समांतर होती हैं परस्पर समांतर होती हैं।