11.1 एक लंब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल

अभी तक हम सर्वांगसम आकृतियों को एक के ऊपर एक रख कर ठोस जनित कर रहे थे। संयोग से इन आकृतियों को प्रिज्म (prism) कहते हैं। अब एक अन्य प्रकार के ठोसों को देखें जो प्रिज्म नहीं हैं। (इस प्रकार के ठोस पिरामिड (pyramids) कहलाते हैं।) आइए देखें कि इनको किस प्रकार जनित किया (बनाया) जाता है।

क्रियाकलाप : एक समकोण त्रिभुज $\mathrm{ABC}$ जिसका कोण $\mathrm{B}$ समकोण हो, काट लीजिए। दोनों लंब भुजाओं में से किसी एक, मान लीजिए $A B$, के अनुदिश एक लंबी और मोटी डोरी चिपका दीजिए [देखिए आकृति 11.1(a)]। डोरी को दोनों हाथों से त्रिभुज के दोनों ओर से पकड़े हुए, त्रिभुज को डोरी के अनुदिश कई बार घुमाइए। आप क्या देखते हैं? जब त्रिभुज डोरी के अनुदिश घूम रहा है, तो जो वह आकृति बना रहा है, क्या आप उसे पहचानते हैं [देखिए आकृति 11.1(b)]? क्या आपको इस बात की याद दिलाती है कि इसी आकार के एक छोटे बर्तन (पात्र) में भरी आपने कभी आइसक्रीम खाई थी [देखिए आकृति 11.1 (c) और (d)]?

(a)

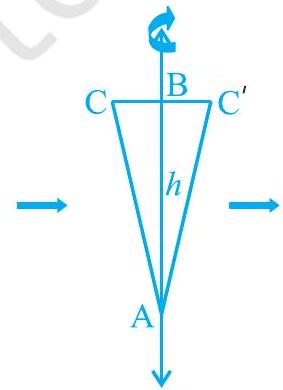
(b)

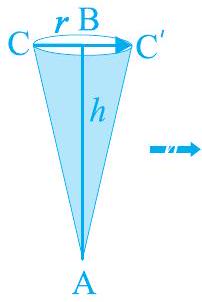
(c)

(d)

आकृति 11.1

यह आकृति एक लंब वृत्तीय शंकु (right circular cone) कहलाती है। आकृति 11.1(c) में बिन्दु A इस लम्ब वृत्तीय शंकु का शीर्ष (vertex) कहलाता है, $\mathrm{AB}$ इसकी ऊँचाई कहलाती है और $\mathrm{BC}$ आधार की त्रिज्या कहलाती है। $\mathrm{AC}$ इस शंकु की तिर्यक ऊँचाई (slant height) कहलाती है। यहाँ $\mathrm{B}$ वृत्तीय आधार का केंद्र (centre) है। शंकु की ऊँचाई, त्रिज्या और तिर्यक ऊँचाई को प्रायः क्रमशः $h, r$ और $l$ से व्यक्त किया जाता है। एक बार पुन: देखें कि किस प्रकार के शंकु को हम लंब वृत्तीय शंकु नहीं कह सकते हैं। आप आकृति

(b)

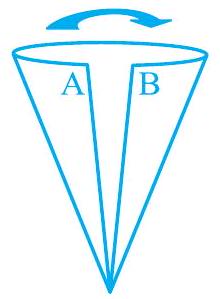
आकृति 11.2 11.2 को देखिए। इनमें जो आप शंकु देख रहे हैं वे लंब वृत्तीय शंकु नहीं हैं। (a) में, शीर्ष को आधार के केंद्र से मिलाने वाली रेखा आधार पर लंब नहीं है और (b) में, आधार वृत्तीय नहीं है।

जैसा कि बेलन की स्थिति में था, जब तक अन्यथा न कहा जाए, ‘शंकु’ से हमारा तात्पर्य लंब वृत्तीय ‘शंकु’ से ही होगा।

क्रियाकलाप : (i) एक साफ बने हुए कागज़ के शंकु को उसके शीर्ष से जाने वाली किसी भुजा या किनारे के अनुदिश काटिए जिसमें कोई अतिव्यापिकता न हो तथा खोल कर देखिए कि किस आकार के कागज़ से शंकु का पृष्ठ बना था। (जिस भुजा या किनारे के अनुदिश आप शंकु को काटेंगे वह उसकी तिर्यक ऊँचाई होगी जिसे $l$ से व्यक्त किया जाता है।) खोला हुआ कागज़ आपको एक गोल केक के भाग की तरह दिखाई देगा।

(ii) यदि आप उन भुजाओं, जिनके सिरों पर $\mathrm{A}$ और $\mathrm{B}$ अंकित है, को मोड़ कर मिला लें, तो आप देखेंगे कि आकृति 11.3 (c) का वक्रित भाग शंकु का वृत्तीय आधार बनाता है।

(a)

(b)

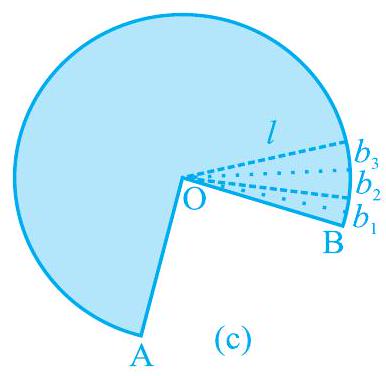
आकृति 11.3 (iii) यदि आकृति 11.3 (c) में दिए कागज़ को $\mathrm{O}$ से जाती हुई रेखाओं द्वारा सैकड़ों छोटे-छोटे टुकड़ों में विभाजित कर लिया जाए, तो ये कटे हुए भाग लगभग त्रिभुज के आकारों के हैं और इनमें से प्रत्येक की ऊँचाई शंकु की तिर्यक ऊँचाई $l$ के बराबर है।

(iv) अब प्रत्येक त्रिभुज का क्षेत्रफल $=\frac{1}{2} \times$ प्रत्येक त्रिभुज का आधार $\times l$

अतः, पूरे कागज़ का क्षेत्रफल

$=$ सभी त्रिभुजों के क्षेत्रफलों का योग

$=\frac{1}{2} b _{1} l+\frac{1}{2} b _{2} l+\frac{1}{2} b _{3} l+\quad=\frac{1}{2} l\left(b _{1}+b _{2}+b _{3}+\quad\right)$

$=\frac{1}{2} \times l \times$ [आकृति $11.3(\mathrm{c})$ की पूरी वक्रित परिसीमा की लंबाई]

(चूँकि $b _{1}+b _{2}+b _{3}+\ldots$ मिलकर इस आकृति के वक्रित भाग को बनाते हैं)

परन्तु इस वक्रित भाग से शंकु का आधार बनता है।

साथ ही, इस आधार की परिधि $=2 \pi r$, जहाँ $r$ आधार की त्रिज्या है।

इसलिए,

शंकु का वक्र पृष्ठीय क्षेत्रफल $=\frac{1}{2} \times l \times 2 \pi r=\pi r l$

जहाँ $r$ आधार की त्रिज्या है और $l$ तिर्यक ऊँचाई हैं।

ध्यान दीजिए कि $l^{2}=r^{2}+h^{2}$ होता है, जिसे हम आकृति 11.4 से देख सकते हैं ( पाइथागोरस प्रमेय से)। यहाँ $h$ शंकु की ऊँचाई है।

अत: $l=\sqrt{r^{2}+h^{2}}$ होगा।

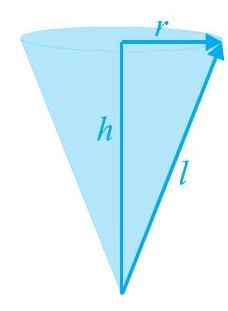
आकृति 11.4

अब यदि शंकु के आधार को बंद रखा जाता है, तो ढकने के लिए $r$ त्रिज्या वाले एक वृत्ताकार कागज के टुकड़े की आवश्यकता और होगी। इसका क्षेत्रफल स्पष्टतः $\pi r^{2}$ है।

इसलिए, शंकु का कुल पृष्ठीय क्षेत्रफल $=\pi r l+\pi r^{2}=\pi r(l+r)$

11.2 गोले का पृष्ठीय क्षेत्रफल

एक गोला (sphere) क्या होता है? क्या यह एक वृत्त की तरह ही है? क्या आप एक कागज पर वृत्त खींच सकते हैं? हाँ, आप खींच सकते हैं, क्योंकि यह एक बंद समतल आकृति है जिसका प्रत्येक बिंदु एक निश्चित बिंदु (जिसे वृत्त का केंद्र कहते हैं) से एक निश्चित दूरी पर रहता है (जिसे वृत्त की त्रिज्या कहते हैं)। अब यदि आप एक वृत्ताकार चकती (disc) के एक व्यास के अनुदिश एक डोरी चिपका दें और इसे वैसे ही घुमाएँ जैसे आपने पिछले अनुच्छेद में त्रिभुज को घुमाया था, तो आप एक नया ठोस देखेंगे (देखिए आकृति 11.6)। यह किस वस्तु से मिलता-जुलता लगता है? एक गेंद? हाँ, ऐसा ही है। यह एक गोला (sphere) कहलाता है।

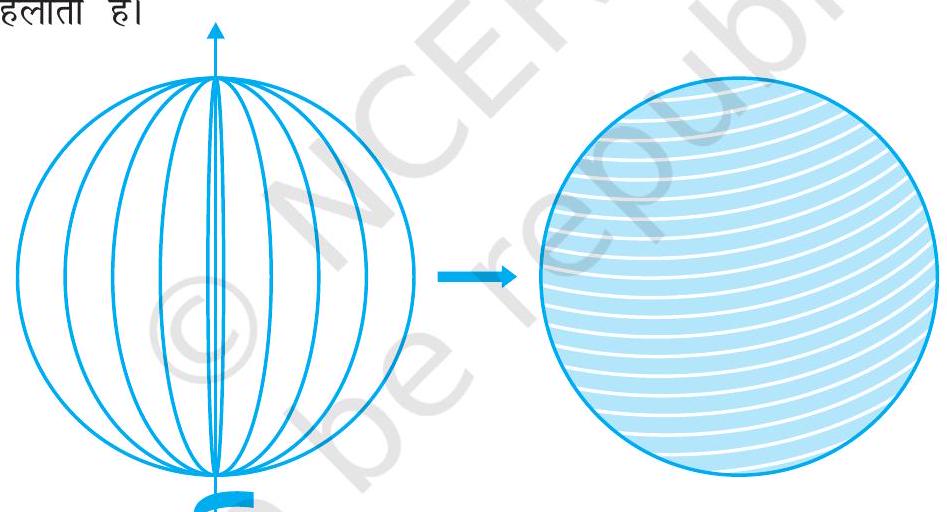
आकृति 11.6

क्या आप अनुमान लगा सकते हैं कि उस वृत्त के केंद्र का क्या होता है जिसे आपने घुमाया है। निःसंदेह, यह गोले का केंद्र भी हो जाता है। इस प्रकार, गोला एक त्रिविमीय आकृति (three dimensional figure) ( ठोस आकृति) है, जो आकाश ( स्पेस) (space) में स्थित उन सभी बिंदुओं से मिल कर बनी है जो एक निश्चित बिंदु से (जो गोले का केन्द्र कहलाता है) से एक अचर या निश्चित दूरी पर होते हैं ( जो गोले की त्रिज्या कहलाती है)।

टिप्पणी : गोला एक गेंद की पृष्ठ की तरह होता है। ठोस गोला उस ठोस के लिए प्रयोग होता है जिसका पृष्ठ एक गोला हो।

क्रियाकलाप : क्या आप कभी लट्टू के साथ खेले हैं या कभी आपने किसी व्यक्ति को लट्टू के साथ खेलते देखा है? आप यह जानते होंगे कि उस पर डोरी किस प्रकार लपेटी जाती है। अब आइए एक रबर की गेंद लें और उसके ऊपर एक कील लगा दें। कील की सहायता लेते हुए, गेंद पर डोरी लपेटना प्रारम्भ कर दीजिए। जब आप ऐसा कर रहे हों, तो डोरी को थामे रखने के लिए, बीच-बीच में पिन लगाते रहिए और डोरी लपेटना तब तक जारी रखिए जब तक कि पूरी गेंद पर डोरी न लिपट जाए [देखिए आकृति 11.7(a)]। डोरी पर प्रारम्भिक और अंतिम बिंदु अंकित कर लीजिए और धीरे-धीरे गेंद से डोरी को हटा लीजिए। अब अपने शिक्षक से गेंद का व्यास मापने के लिए सहायता देने के लिए कहिए। इससे आपको गेंद की त्रिज्या ज्ञात हो जाएगी। इसके बाद, कागज पर गेंद की त्रिज्या के बराबर चार वृत्त खींच लीजिए। अब जो डोरी आपने गेंद पर लपेटी थी उसी को एक-एक करके इन वृत्तों पर रखकर वृत्तों को भरिए [देखिए आकृति 11.7(b)]।

(a)

(b)

आकृति 11.7

इन सबसे आपको क्या प्राप्त होता है?

वह डोरी जिसने एक गोले के पृष्ठ को पूरा-पूरा ढक दिया था अब उसी गोले की त्रिज्या वाले चार वृत्तों के क्षेत्रों को भर रही है। इसका क्या अर्थ हुआ? इससे यह सुझाव मिलता है कि त्रिज्या $r$ वाले एक गोले का पृष्ठीय क्षेत्रफल

$$ =\text { त्रिज्या } r \text { वाले चार वृत्तों का क्षेत्रफल }=4 \times\left(\pi r^{2}\right) $$

इसलिए, गोले का पृष्ठीय क्षेत्रफल $=4 \pi r^{2}$

जहाँ $r$ गोले की त्रिज्या है।

गोले के पृष्ठ पर आप कितने फलक देखते हैं? केवल एक। यह वक्रीय है।

आइए एक ठोस गोला लें और इसे बीच से इसके केंद्र से जाते हुए एक तल द्वारा दो भागों में काट लें। गोले का क्या होता है? यह दो बराबर भागों में विभाजित हो गया है (देखिए आकृति 11.8)। प्रत्येक आधा भाग क्या कहलाता है यह एक अर्धगोला (hemisphere) कहलाता है (क्योंकि hemi का अर्थ आधा है।)। अर्धगोले के पृष्ठ के बारे में आप क्या कह सकते हैं? इसके कितने फलक हैं?

आकृति 11.8

दो!, इनमें एक वक्रीय है और एक समतल फलक है (आधार)।

अर्धगोले का वक्र पृष्ठीय क्षेत्रफल गोले के पृष्ठीय क्षेत्रफल का आधा, अर्थात् $\frac{1}{2} \times 4 \pi r^{2}$ है।

अतः, अर्धगोले का वक्र पृष्ठीय क्षेत्रफल $=2 \pi r^{2}$

जहाँ $r$ उस गोले की त्रिज्या है जिसका अर्धगोला एक भाग है।

अब दोनों फलकों को लेने पर, इसका कुल पृष्ठीय क्षेत्रफल $=2 \pi r^{2}+\pi r^{2}$ है।

अतः, अर्धगोले का कुल पृष्ठीय क्षेत्रफल $=3 \pi r^{2}$

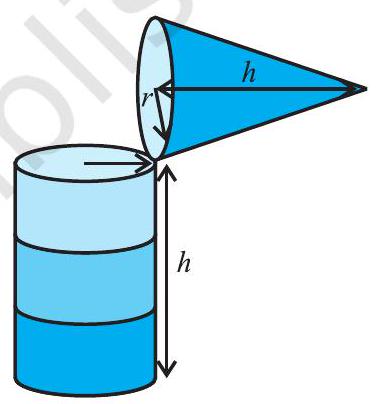
क्रियाकलाप : उपरोक्त आकृतियों की ही तरह, एक ही आधार त्रिज्या और एक ही ऊँचाई वाला एक खोखला बेलन और एक खोखला शंकु बनाने का प्रयत्न कीजिए (देखिए आकृति 11.11)। फिर हम एक प्रयोग द्वारा यह ज्ञात करेंगे कि एक शंकु का आयतन क्या है। आइए इस प्रयोग को प्रारम्भ करें।

शंकु को रेत से एक बार ऊपर तक भरिए और इस रेत को बेलन में डाल दीजिए। हम देखते हैं कि इससे बेलन का कुछ भाग भर गया है [देखिए आकृति 11.12 (a)]।

फिर हम दुबारा शंकु को रेत से भर कर बेलन में रेत को डाल देते हैं। हम देखते हैं कि बेलन अभी भी पूरा नहीं भरा है [देखिए आकृति 11.12(b)]।

अब शंकु को तीसरी बार रेत से भर कर बेलन में डालिए। हम देखते हैं कि बेलन पूरा रेत से भर गया है [देखिए आकृति 11.12(c)]।

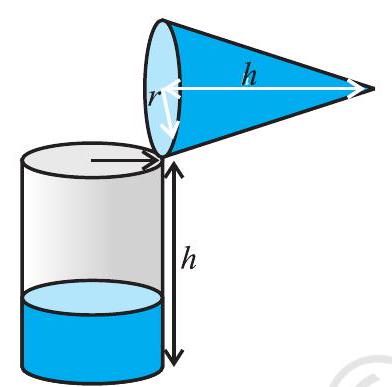
(a)

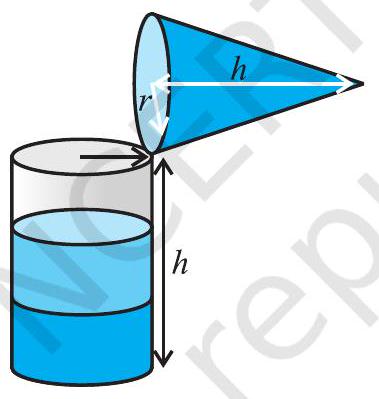
(b)

(c)

आकृति 11.12

इस प्रयोग से, हम निष्कर्ष निकाल सकते हैं कि तीन शंकुओं का आयतन बेलन के आयतन के बराबर है। इसका अर्थ है कि यदि शंकु और बेलन की आधार त्रिज्या एक ही हो और ऊँचाई भी एक ही हो, तो शंकु का आयतन बेलन के आयतन का एक-तिहाई होता है।

अतः, शंकु का आयतन $=\frac{1}{3} \pi r^{2} h$

जहाँ $r$ आधार त्रिज्या है और $h$ शंकु की ऊँचाई है।

11.4 गोले का आयतन

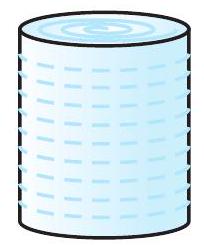
आइए अब देखें कि एक गोले का आयतन कैसे मापा जाए। पहले विभिन्न त्रिज्याओं वाले दो या तीन गोले लीजिए। फिर एक बर्तन लीजिए, जिसके अंदर इन गोलों को (केवल एक बार में एक) रखा जा सके। साथ ही, एक बड़ी नाँद (trough) लीजिए जिसमें इस बर्तन को रखा जा सके। अब बर्तन को पूरा ऊपर तक पानी से भरिए [देखिए आकृति 11.13(a)]।

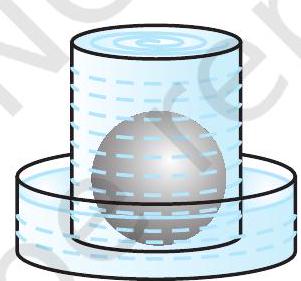
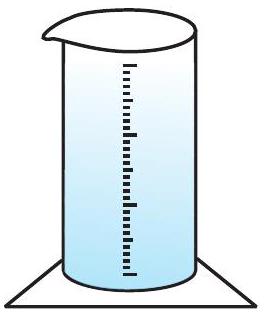
अब लिए गए गोलों में से एक को बर्तन में सावधानीपूर्वक डालिए। बर्तन में से कुछ पानी बाहर निकल कर उस नाँद में जाएगा जिसमें वह बर्तन रखा हुआ है [देखिए आकृति 11.13(b)]। अब नाँद में आए इस पानी को सावधानीपूर्वक एक नापने वाले बेलन [अर्थात् अशांकित बेलनाकार गिलास (graduated cylindrical jar)] में डालिए। मान लीजिए पानी में डुबाए गए गोले की त्रिज्या $r$ है (आप गोले का व्यास माप कर उसकी त्रिज्या ज्ञात कर सकते हैं)। अब $\frac{4}{3} \pi r^{3}$ का मान निकालिए। क्या आप यह पाते हैं कि यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है?

(a)

(b)

(c)

आकृति 11.13

एक बार फिर इसी प्रक्रिया को एक अन्य माप का गोला लेकर दोहराइए। इस गोले की त्रिज्या $R$ ज्ञात करके $\frac{4}{3} \pi R^{3}$ का मान निकालिए। एक बार फिर यह मान बर्तन से बाहर निकले पानी के आयतन के लगभग बराबर है। यह हमें क्या बताता है? हम जानते हैं कि गोले का आयतन उसके द्वारा हटाए गए पानी के आयतन के बराबर है। इस प्रयोग को बार-बार करने पर, हम प्राप्त करते हैं कि एक गोले का आयतन गोले की त्रिज्या के घन का $\frac{4}{3} \pi$ गुना है। इससे हमें निम्न सुझाव प्राप्त होता है :

$$ \text { गोले का आयतन }=\frac{4}{3} \pi r^{3} $$

जहाँ $r$ गोले की त्रिज्या है।

उच्चतर कक्षाओं में इसे सिद्ध भी किया जा सकता है। परन्तु इस समय तो हम इसे सत्य मान लेते हैं।.

अब अर्धगोले के आयतन के बारे में आप क्या अनुमान लगा सकते हैं? हाँ, यह $\frac{4}{3} \pi r^{3}$ का $\frac{1}{2}=\frac{2}{3} \pi r^{3}$ है।

अतः, अर्धगोले का आयतन $=\frac{2}{3} \pi r^{3}$

जहाँ $r$ अर्धगोले की त्रिज्या है।

आइए इन सूत्रों का प्रयोग दर्शाने के लिए कुछ उदाहरण लें।

11.5 सारांश

इस अध्याय में, आपने निम्नलिखित बिंदुओं का अध्ययन किया है:

1. शंकु का वक्र पृष्ठीय क्षेत्रफल $=\pi r l$

2. शंकु का कुल पृष्ठीय क्षेत्रफल $=\pi r l+\pi r^{2}$, अर्थात् $\pi r(l+r)$

3. गोले का पृष्ठीय क्षेत्रफल $=4 \pi r^{2}$

4. अर्धगोले का वक्र पृष्ठीय क्षेत्रफल $=2 \pi r^{2}$

5. अर्धगोले का कुल पृष्ठीय क्षेत्रफल $=3 \pi r^{2}$

6. शंकु का आयतन $=\frac{1}{3} \pi r^{2} h$

7. गोले का आयतन $=\frac{4}{3} \pi r^{3}$

8. अर्धगोले का आयतन $=\frac{2}{3} \pi r^{3}$