अध्याय 13 दोलन
13.1 भूमिका
हम अपने दैनिक जीवन में विभिन्न प्रकार की गतियाँ देखते हैं। इनमें से कुछ जैसे सरल रैखिक गति और किसी प्रक्षेप्य की गति के विषय में तो आप अध्ययन कर ही चुके हैं। ये दोनों ही गतियाँ अनावर्ती होती हैं। हमने एकसमान वर्तुल गति तथा सौर परिवार में ग्रहों की कक्षीय गतियों के विषय में भी अध्ययन कर लिया है। इन उदाहरणों में निश्चित समय-अंतराल के पश्चात् गति की पुनरावृत्ति होती है, अर्थात् यह आवर्ती होती है। आपने बचपन में अपने पालने अथवा झूले पर झूलने का आनन्द लिया होगा। यह दोनों गतियाँ पुनरावर्ती होती हैं, परंतु किसी ग्रह की आवर्ती गति से भिन्न होती हैं। यहाँ वस्तु किसी माध्य स्थिति के इधर-उधर गति करती है । दीवार-घड़ी का लोलक भी इसी प्रकार की गति करता है। इस प्रकार की अग्र-पश्च (आगे-पीछे) आवर्ती गति के प्रचुर उदाहरण हैं- नदी में डूबती-उतरती हुई नाव, वाष्प इंजन में अग्र और पश्च चलता हुआ पिस्टन आदि। इस प्रकार की गति को दोलन गति कहते हैं। इस अध्याय में हम इस गति के बारे में अध्ययन करेंगे ।
दोलन गति का अध्ययन भौतिकी के लिए आधारभूत है; बहुत-सी भौतिक परिघटनाओं को समझने के लिए इसकी संकल्पना की आवश्यकता होती है । वाद्य यंत्रों; जैसे-सितार, गिटार अथवा वायलिन में हम कंपायमान डोरियों द्वारा रोचक ध्वनियाँ उत्पन्न होते हुए देखते हैं। ढोलों में झिल्लियाँ तथा टेलीफोन और ध्वनि विस्तारकों के स्पीकरों में डायफ्राम अपनी माध्य स्थिति के इधर-उधर कंपन करते हैं। वायु के अणुओं के कंपनों द्वारा ही ध्वनि-संचरण संभव हो पाता है। एक ठोस पदार्थ में अणु अपनी माध्य स्थितियों के परितः कम्पन करते हैं, कम्पन की औसत ऊर्जा तापमान के समानुपाती होती है। $\mathrm{AC}$ पावर ऐसी वोल्टता का संभरण करता है जो माध्य मान (शून्य) के धनात्मक तथा ऋणात्मक ओर एकांतर क्रम से दोलायमान रहता है।
किसी आवर्ती गति के व्यापक तथा दोलन गति के विशेष विवरण के लिए कुछ मूल संकल्पनाओं; जैसे-आवर्तकाल, आवृत्ति, विस्थापन, आयाम और कला की आवश्यकता होती है । अगले अनुभाग में इन संकल्पनाओं को विकसित किया गया है ।
13.2 दोलन और आवर्ती गति
चित्र 13.1 में कुछ आवर्ती गतियाँ दर्शाई गई हैं। मान लीजिए कोई कीट किसी रैम्प पर चढ़ता है और गिर जाता है। वह अपने प्रारंभिक स्थान पर आ जाता है और इस प्रक्रिया को बार-बार दोहराता है। यदि आप जमीन से ऊपर इसकी ऊँचाई तथा समय के बीच ग्राफ खींचें तो यह चित्र 13.1(a) की तरह दिखेगा। यदि कोई बालक किसी सीढ़ी पर चढ़े और उतरे तथा इस प्रक्रिया को समान रूप से बार-बार दोहराये तो उसकी ऊँचाई तथा समय के बीच ग्राफ चित्र 13.1(b) के जैसा दिखेगा। जब आप किसी गेंद को अपनी हथेली से जमीन की तरफ बार-बार मारते हैं तो इसकी ऊँचाई और समय के बीच ग्राफ 13.1(c) के जैसा दिखेगा। ध्यान दीजिए कि चित्र 13.1(c) में दोनों वक्रीय भाग न्यूटन की गति समीकरण के अनुसार परवलय के अंश हैं, अनुभाग (2.6) देखिए।
$h=u t+\frac{1}{2} g t^{2}$ अधोमुखी गति के लिए, तथा
$h=u t-\frac{1}{2} g t^{2}$ उपरिमुखी गति के लिए,
इन समीकरणों में $u$ का मान अलग परिस्थितियों के लिए भिन्न होगा। ये सभी आवर्ती गति के उदाहरण हैं। अतः कोई गति जो निश्चित अंतराल के बाद पुनरावृत्ति करती है आवर्ती गति कहलाती है।

चित्र 13.1 आवृत्ति गति के उदाहरण। प्रत्येक अवस्था में आवर्तकाल $T$ दर्शाया गया है।
सामान्यतः आवर्ती गति करने वाले पिण्ड की एक संतुलन अवस्था होती है जो उसके गति के पथ में स्थित होता है। जब पिण्ड इस संतुलन अवस्था में होता है तो उस पर लगने वाला कुल बाह्य बल शून्य होता है। अतः यदि पिण्ड को इस अवस्था में विराम की स्थिति में छोड़ दें तो यह सदैव विरामावस्था में रहेगा। यदि पिण्ड को इस अवस्था से थोड़ा सा विस्थापित करें तो पिण्ड पर एक बल कार्य करने लगता है जो पिण्ड को पुन: उसकी संतुलन-अवस्था की ओर ले जाने का प्रयास करता है और फलस्वरूप पिण्ड में दोलन या कंपन उत्पन्न हो जाता है। उदाहरण के लिए यदि किसी कटोरे में एक गेंद रख दें तो गेंद कटोरे की तली पर संतुलन अवस्था में होती है। यदि इसको इस बिंदु से थोड़ा विस्थापित करें तो गेंद कटोरे में दोलन करने लगती है। प्रत्येक दोलन गति आवर्ती होती है परंतु प्रत्येक आवर्ती गति दोलनीय नहीं होती। वर्तुल गति भी आवर्ती होती है, परंतु दोलनीय नहीं होती है।
दोलन एवं कंपन में कोई मुख्य अंतर नहीं है। साधारणतः जब आवृत्ति का मान कम होता है तो हम गति को दोलनीय कहते हैं (जैसे किसी वृक्ष की टहनी की दोलन गति)। इसके विपरीत जब गति की आवृत्ति अधिक होती है तो हम गति को कंपन कहते हैं। जैसे किसी संगीत वाद्य के तार का कंपन।
सरल आवर्ती गति दोलनीय गति का एक सरल रूप है। यह तब होता है जब किसी दोलनीय वस्तु के ऊपर लगने वाला बल संतुलन अवस्था में इसके विस्थापन के समानुपाती होता है। पुनः वस्तु के दोलन के दौरान यह बल सदैव इस संतुलन अवस्था की तरफ निदेशित होता है। यह संतुलन अवस्था वस्तु की गति की माध्य स्थिति भी होती है।
व्यावहारिक रूप में सभी दोलनीय वस्तुएँ अंततोगत्वा अपनी संतुलन अवस्था को प्राप्त कर लेती हैं। क्योंकि इनकी गति में घर्षण तथा अन्य क्षयकारी बलों के कारण अवमंदन उत्पन्न होता है। परंतु कोई बाह्य आवर्ती बल लगाकर हम वस्तु को दोलनीय अवस्था में रख सकते हैं। इस पाठ के अंतिम अनुभागों में हम अवमंदित तथा प्रणोदित दोलनों का अध्ययन करेंगे।
किसी भी द्रव्यात्मक माध्यम को हम युग्मित दलित्रों का एक बड़ा समूह मान सकते हैं। इन दलित्रों के सामूहिक दोलन तरंग का रूप लेते हैं। जल तरंग, भूकम्पित तरंगें, विद्युत चुंबकीय तरंगें इन तरंगों के उदाहरण हैं। तरंगीय घटनाओं के विषय में हम अगले अध्याय में अध्ययन करेंगे।
13.2.1 आवर्तकाल तथा आवृत्ति
हमने देखा है कि कोई गति जिसकी किसी नियमित समय अंतराल पर स्वयं पुनरावृत्ति होती है आवर्ती गति कहलाती है। वह न्यूनतम समय अंतराल जिसके पश्चात् गति की पुनरावृत्ति होती है, इसका आवर्तकाल कहलाता है। अतः समय को हम $T$ द्वारा दर्शाते हैं। इसका SI मात्रक सेकंड है । उन आवर्ती गतियों के लिए, जो सेकंडों के पैमाने पर या तो बहुत तीव्र अथवा बहुत मंद होती हैं, समय के अन्य सुविधाजनक मात्रक उपयोग में लाए जाते हैं। किसी क्वार्ट्ज़ क्रिस्टल का कंपन काल माइक्रोसेकंड $\left(10^{-6} \mathrm{~s}\right)$ के मात्रकों, जिसका प्रतीक $\mu \mathrm{s}$ है, में व्यक्त किया जाता है । इसके विपरीत बुध ग्रह की कक्षीय अवधि 88 भू-दिवस होती है। हेली धूमकेतु हर 76 वर्ष के पश्चात् पुन: दृष्टिगोचर होता है ।
आवर्तकाल ’ $T$ ’ के व्युत्क्रम से हमें प्रति इकाई समय में दोलनों की संख्या प्राप्त होती है। यह राशि आवर्ती गति की आवृत्ति कहलाती है । इसे प्रतीक $v$ द्वारा निरूपित किया जाता है। $v$ तथा $T$ के मध्य निम्नलिखित पारस्परिक संबंध होता है:
$$ \begin{equation*} v=\frac{1}{T} \tag{13.1} \end{equation*} $$
इस प्रकार $v$ का मात्रक $\left(\mathrm{s}^{-1}\right)$ है । रेडियो तरंगों के आविष्कारक हेनरिख रुडोल्फ हर्ट्ज़ (1857-1894) के नाम पर आवृत्ति के मात्रक को एक विशेष नाम दिया गया। इसे हर्ट्ज़ (hertz प्रतीक $\mathrm{Hz}$ ) कहते हैं । इस प्रकार,
1 हर्ट्ज़ $=1 \mathrm{~Hz}=1$ दोलन प्रति सेकंड $=1 \mathrm{~s}^{-1}$ नहीं है ।
ध्यान दीजिए, आवृत्ति का सदैव ही पूर्णांक होना आवश्यक
उदाहरण 13.1 कोई मानव हृद्य एक मिनट में औसतन 75 बार धड़कन करता पाया जाता है । इसकी आवृत्ति तथा आवर्तकाल परिकलित कीजिए ।
हल हृदय की धड़कन की आवृत्ति $=75 /(1$ मिनट $)$
$$ \begin{aligned} & =75 /(60 \mathrm{~s}) \\ & =1.25 \mathrm{~s}^{-1} \\ & =1.25 \mathrm{~Hz} \\ \text { आवर्तकाल } T \quad & =1 /\left(1.25 \mathrm{~s}^{-1}\right) \\ & =0.8 \mathrm{~s} \end{aligned} $$
13.2.2 विस्थापन
अनुभाग 3.2 में हमने किसी कण के विस्थापन को उसके स्थिति सदिश में परिवर्तन के रूप में परिभाषित किया था। इस अध्याय में हम विस्थापन नामक इस पद का उपयोग अधिक व्यापक अर्थों में करेंगे । यह किसी भी विचारणीय भौतिक गुण में समय के साथ परिवर्तन को निरूपित करेगा । उदाहरण के लिए, एक पृष्ठ पर किसी स्टील बॉल की सरल रेखीय गति के लिए, समय के फलन के रूप में आरंभ बिंदु से बॉल की दूरी इसका स्थिति-विस्थापन है । मूल बिंदु का चुनाव सुविधानुसार किया जा सकता है । मान लीजिए कोई गुटका किसी कमानी से जुड़ा है जिसका दूसरा सिरा किसी दृढ़ दीवार से संबद्ध है [देखिए चित्र 13.2 (a)] साधारणतः किसी पिण्ड का विस्थापन इसकी संतुलन अवस्था से मापना सरल होगा। किसी दोलायमान सरल लोलक के लिए, समय के फलन के रूप में ऊर्ध्वाधर से कोण को विस्थापन-चर के रूप में निरूपित किया जा सकता है [देखिए चित्र 13.2(b)]। ‘विस्थापन’ पद का उल्लेख सदैव स्थिति के संदर्भ में ही नहीं किया जाता। विस्थापन चर कई अन्य प्रकार के भी हो सकते हैं । किसी a.c. परिपथ में संयोजित संधारित्र के सिरों के बीच समय के साथ परिवर्तित हो रही “वोल्टता” को भी एक विस्थापन चर के रूप में लिया जा सकता है । इसी प्रकार, ध्वनि तरंगों के संचरण में समय के साथ ‘दाब’ में परिवर्तन, प्रकाश तरंगों में परिवर्तित हो रहे वैद्युत तथा चुंबकीय क्षेत्र अन्य संदर्भो में विस्थापन के उदाहरण हैं। विस्थापन चर का मान धनात्मक या ऋणात्मक हो सकता है। दोलनों के प्रयोगों में, भिन्न समयों के लिए विस्थापन चरों की माप ली जाती है ।

चित्र 13.2(a) कोई गुटका किसी कमानी से संलग्न, जिसका दूसरा सिरा किसी दृढ़ दीवार से संबद्ध है । गुटका घर्षण रहित पृष्ठ पर गति करता है। गुटके की गति को दीवार से दूरी, अथवा विस्थापन $\boldsymbol{X}$ के पदों में व्यक्त किया जा सकता है ।

चित्र $13.2(b)$ एक दोलायमान सरल लोलक, इसकी गति को ऊर्ध्वाधर से कोणीय विस्थापन $\theta$ के पदों में व्यक्त किया जा सकता है ।
विस्थापन को सदैव ही समय के गणितीय फलन द्वारा निरूपित किया जा सकता है । आवर्ती गतियों में यह फलन समय का आवर्ती होता है । आवर्ती फलनों में से एक सरलतम आवर्ती फलन को निम्न प्रकार से व्यक्त कर सकते हैं,
$$ \begin{equation*} f(t)=A \cos \omega t \tag{13.3a} \end{equation*} $$
यदि इस फलन के कोणांक, $\omega t$, में $2 \pi$ रेडियन या इसके किसी पूर्णांक गुणज की वृद्धि कर दी जाए, तो फलन का मान वही $f$ रहता है । तब भी फलन $f(t)$ आवर्ती ही रहता है जिसका आवर्तकाल, $T$ निम्नलिखित होगा,
$$ \begin{equation*} T=\frac{2 \pi}{\omega} \tag{13.3b} \end{equation*} $$
अतः कोई फलन $f(t)$ काल $T$ का आवर्ती होता है,
$$ f(t)=f(t+T) $$
यदि हम ज्या $(\sin )$ फलन, $f(t)=A \sin \omega t$ भी लें तो स्पष्ट रूप से यही परिणाम सही होता है । साथ ही ज्या (sin) एवं कोज्या (cos) फलनों का एक घात संचय, जैसे
$$ \begin{equation*} f(t)=A \sin \omega t+B \cos \omega t \tag{13.3c} \end{equation*} $$
भी आवर्ती फलन होता है, जिसका आवर्तकाल $T$ होता है । यदि हम
$$ A=D \cos \phi \text { तथा } B=D \sin \phi $$
लें, तो समीकरण (13.3c) को इस प्रकार लिख सकते हैं
$$ \begin{equation*} f(t)=D \sin (\omega t+\phi), \tag{13.3d} \end{equation*} $$
यहाँ अचर $D$ और $\phi$ दिए गए हैं
$$ D=\sqrt{A^{2}+B^{2}} \text { तथा } \phi=\tan ^{-1}\left(\frac{B}{A}\right) $$
आवर्ती ज्या और कोज्या फलनों का विशेष महत्त्व फ्रांसीसी गणितज्ञ जीन बापटिस्ट जोसेफ फूरिए (1768-1830) द्वारा सिद्ध असाधारण परिणाम के कारण है, जो इस प्रकार है : किसी भी आवर्ती फलन को उचित गुणांक वाले विभिन्न आवर्तकाल के ज्या व कोज्या फलनों के अध्यारोपण द्वारा व्यक्त किया जा सकता है ।
उदाहरण 13.2 निम्नलिखित समय के फलनों में कौन (a) आवर्ती तथा (b) अनावर्ती गति को निरूपित करते हैं ? प्रत्येक आवर्ती गति का आवर्तकाल लिखिए [ $\omega$ कोई धनात्मक नियतांक है] ।
(i) $\sin \omega t+\cos \omega t$
(ii) $\sin \omega t+\cos 2 \omega t+\sin 4 \omega t$
(iii) $\mathrm{e}^{-\omega t}$
(iv) $\log (\omega t)$
हल
(i) $\sin \omega t+\cos \omega t$ एक आवर्ती फलन है। इसे $\sqrt{2} \sin \left(\omega \mathrm{t}+\frac{\pi}{4}\right)$ के रूप में भी व्यक्त किया जा सकता है।
अब, $\sqrt{2} \sin (\omega t+\pi / 4)=\sqrt{2} \sin (\omega t+\pi / 4+2 \pi)$
$$ =\sqrt{2} \sin \left[\omega\left(t+\frac{2 \pi}{\omega}\right)+\frac{\pi}{4}\right] $$
इस फलन का आवर्तकाल $\frac{2 \pi}{\omega}$ है ।
(ii) यह आवर्ती गति का एक उदाहरण है । ध्यान दीजिए, यहाँ प्रत्येक पद एक विभिन्न कोणीय आवृत्ति के आवर्ती फलन को निरूपित करता है । चूँकि आवर्तकाल वह न्यूनतम समय अंतराल होता है जिसके पश्चात् फलन अपने मान की स्वयं पुनरावृत्ति करता है, $\sin \omega t$ का आवर्तकाल $T _{0}=2 \pi / \omega ; \cos 2 \omega t$ का आवर्तकाल $\pi / \omega=T _{0} / 2$; तथा $\sin 4 \omega t$ का आवर्तकाल $2 \pi /$ $4 \omega=T _{0} / 4$ होता है । प्रथम पद का आवर्तकाल अंतिम दो पदों के आवर्तकालों का गुणनफल होता है। अतः अंतिम समय का निम्न अंतराल जिसके उपरांत तीनों पदों का योग पुनरावृत्ति करता है $T _{0}$ होता है जिसका आवर्त काल $2 \pi / \omega$ है।
(iii) फलन $\mathrm{e}^{-\omega t}$ अनावर्ती है, यह समय में वृद्धि के साथ एक दिष्टतः घटता है तथा $t \rightarrow \infty$ होने पर शून्य की ओर प्रवृत्त होता है और इस प्रकार कभी भी अपने मान की पुनरावृत्ति नहीं करता ।
(iv) फलन $\log (\omega t)$ समय के साथ एकदिष्टतः बढ़ता है । अतः यह अपने मान की कभी भी पुनरावृत्ति नहीं करता और यह एक अनावर्ती फलन है । ध्यान दीजिए, $t \rightarrow \infty$ होने पर $\log \omega t$ अपसारित होकर $\infty$ तक पहुँच जाता है। अतः यह किसी भी प्रकार के भौतिक विस्थापन को निरूपित नहीं कर सकता।
13.3 सरल आवर्त गति
हम चित्र 13.3 के अनुसार $x$-अक्ष के मूल बिंदु पर $+A$ और $-A$ चरम सीमाओं के मध्य अग्र और पश्च कंपन करने वाले किसी कण पर विचार करें । इस दोलायमान गति को सरल आवर्त गति कहते हैं, यदि मूल बिन्दु से कण का विस्थापन $x$ समय के साथ निम्न समीकरण के अनुसार परिवर्तित हो:
$$ \begin{equation*} x(t)=A \cos (\omega t+\phi) \tag{13.4} \end{equation*} $$

चित्र $13.3 x$-अक्ष के मूल बिंदु पर $+A$ और $-A$ सीमाओं के भीतर अग्र और पश्च कंपन करते हुए कोई कण ।
यहाँ $A, \omega$ तथा $\phi$ स्थिरांक हैं।
अतः प्रत्येक आवर्त गति सरल आवर्त गति (SHM) नहीं है; केवल ऐसी आवर्त गति जिसमें विस्थापन-समय का फलन ज्यावक्रीय है, सरल आवर्त गति होती है। चित्र 13.4 में सरल आवर्त गति करते हुए एक कण की समय के असतत् मानों पर स्थिति दर्शायी गई है। प्रत्येक समय अन्तराल $T / 4$ है जहाँ $T$ गति का आवर्तकाल है। चित्र 13.5 में $x$ के साथ $t$ का ग्राफ आलेखित है जो समय के सतत फलन के रूप में कण के विस्थापन का मान देती है। राशियाँ $A, \omega$ तथा $\phi$ जो दी गई आवर्त गति की विशेषता बताती हैं, के मानक नाम हैं, जैसा कि चित्र 13.6 में संक्षिप्त किया गया है। आइए, इन राशियों को हम समझें।

चित्र 13.4 सरल आवर्त गति करते हुए समय के असतत मान $t=$ O. $T / 4, T / 2,3 T / 4, T, 5 T / 4$ पर कण की स्थिति। वह समय जिसके पश्चात गति की पुनरावृत्ति होती है, $T$ कहलाती है। प्रारंभिक स्थिति $(t=0)$ आप कुछ भी चुनें, $T$ का मान स्थिर रहेगा। कण की चाल शून्य विस्थापन ( $x=0$ पर) पर अधिकतम तथा गति की चरम स्थितियों पर शून्य होती है।
SHM का आयाम $A$, कण के अधिकतम विस्थापन का परिमाण होता है। [ध्यान दें, व्यापकीकृकता के बिना किसी नुकसान के, $A$ को धनात्मक लिया जा सकता है]।

चित्र 13.5 सरल आवर्त गति करते हुए कण का विस्थापन समय के सतत फलन के रूप में

चित्र 13.6 समीकरण (13.4) में दिए मानक संकेतों का अर्थ
चूंकि समय का कोज्या फलन +1 से -1 के बीच विचरण करता है, इसलिए विस्थापन चरम स्थिति $+A$ से $-A$ के बीच विचरण करेगा। दो सरल आवर्त गतियों के $\omega$ तथा $\phi$ समान, लेकिन आयाम अलग हो सकते हैं, जैसा कि चित्र 13.7(a) में दिखाया गया है।

चित्र 13.7 (a) समीकरण (13.4) से प्राप्त $\phi=0$ पर समय के फलन के रूप में विस्थापन का आलेख। वक्र 1 और 2 दो भिन्न आयामों $A$ तथा $A$ के लिए हैं ।
जब किसी दिए गए आवर्त गति का आयाम $A$ नियत है, किसी समय $t$ पर कण की गति की आवस्था को कोज्या फलन के कोणांक $(\omega t+\phi)$ के द्वारा दर्शाया जाता है। समय पर आश्रित रहने वाली इस राशि $(\omega t+\phi)$ को गति की कला कहते हैं। $t=0$ पर कला का परिमाण $\phi$ होता है जिसे कला नियतांक (अथवा कला-कोण) कहते हैं। यदि आयाम ज्ञात हो तो $t=0$ पर के विस्थापन मान से $\phi$ ज्ञात किया जा सकता है। दो सरल आवर्त गतियों के $A$ तथा $\omega$ समान लेकिन कला-कोण $\phi$ विभिन्न हो सकते हैं, जैसा कि चित्र 13.7 (b) में दर्शाया गया है।
अंततः राशि $\omega$ को गति के आवर्तकाल $T$ से संबंधित देखा जा सकता है। सरलता के लिए समीकरण (13.4) में $\phi$ $=0 \mathrm{rad}$ लेने पर हमें प्राप्त होता है-

चित्र 13.7(b) समीकरण (13.4) से प्राप्त $(x-t)$ आलेख । वक्र 3 तथा 4 क्रमशः कला कोण $\phi=0 \mathrm{rad}$ तथा $\phi=-\pi / 4 \mathrm{rad}$ के लिए हैं। दोनों आलेखों के लिए आयाम $A$ समान है।
$$ \begin{equation*} x(t)=A \cos \omega t \tag{13.5} \end{equation*} $$
चूंकि गति का आवर्तकाल $T$ है, $x(t)$ का मान $x(t+T)$ के समान होगा। अर्थात्,
$$ \begin{equation*} A \cos \omega t=A \cos \omega(t+T) \tag{13.6} \end{equation*} $$
अब चूँकि $2 \pi$ आवर्त काल वाला कोज्या फलन आवर्ती है, अर्थात् जब कोणांक $2 \pi$ रेडियन से परिवर्तित होता है, यह प्रथम बार स्वयं की पुनरावृत्ति करता है। अतः
$$ \begin{equation*} \omega(t+T)=\omega t+2 \pi \tag{13.7} \end{equation*} $$
$$ \text{अर्थात् } \quad \omega=2 \pi / T \tag{13.7}$$
$\omega$ को SHM की कोणीय आवृत्ति कहते हैं। इसका S.I. मात्रक रेडियन प्रति सेकेंड है। चूंकि दोलन की आवृत्ति मात्र 1/ $T$ है, $\omega$ दोलन की आवृत्ति का $2 \pi$ गुणा होता है। दो सरल आवर्त गति के $A$ तथा $\phi$ समान, किन्तु $\omega$ विभिन्न हो सकते हैं, जैसा कि चित्र 13.8 में देखा जा सकता है। इस आलेख में वक्र $b$ का आवर्त काल वक्र $a$ के आवर्त काल का आधा है जबकि इसकी आवृत्ति वक्र $a$ की आवृत्ति की दुगुनी है।

चित्र 13.8 समीकरण (14.4) के $\phi=O \mathrm{rad}$ पर दो भिन्न आवर्तकालों के लिए आलेख।
उदाहरण 13.3 समय के निम्नलिखित फलनों में से कौन (a) सरल आवर्त गति तथा (b) आवर्ती गति को निरूपित करता है परंतु सरल आवर्त गति नहीं ? प्रत्येक का आवर्तकाल निकालिए।
(1) $\sin \omega t-\cos \omega t$
(2) $\sin ^{2} \omega t$
हल
(a) $\sin \omega t-\cos \omega t$
$$ \begin{aligned} &= \sin \omega t-\sin (\pi / 2-\omega t) \\ &= 2 \cos (\pi / 4) \sin (\omega t-\pi / 4) \\ &=\sqrt{ } 2 \sin (\omega t-\pi / 4) \end{aligned} $$
यह फलन सरल आवर्त गति का निरूपण करता है, जिसका आवर्तकाल $T=2 \pi / \omega$ तथा कला-कोण $(-\pi / 4) \mathrm{rad}$ अथवा $(7 \pi / 4) \mathrm{rad}$ है ।
(b) $\sin ^{2} \omega t=1 / 2-1 / 2 \cos 2 \omega t$
यह फलन आवर्ती है, जिसका आवर्तकाल $T=\pi / \omega$ है। ये संतुलन बिंदु शून्य के बदले $1 / 2$ पर सरल आवर्त गति को भी दर्शाता है।
13.4 सरल आवर्त गति तथा एकसमान वर्तुल गति
इस अनुभाग में हम देखेंगे कि वृत्त के व्यास पर एकसमान वर्तुल गति का प्रक्षेप सरल आवर्त गति करता है। एक सरल प्रयोग (चित्र 13.9) इस संबंध की सजीव कल्पना करने में हमारी मदद करता है। एक गेंद को किसी डोरी के सिरे से बाँधकर क्षैतिज तल में उसे किसी निश्चित बिंदु के परितः अचर कोणीय चाल से गति कराइये। तब गेंद क्षैतिज तल में एकसमान वर्तुल गति करेगी। अपनी आंख को गति के तल पर केन्द्रित रखते हुए तिरछी ओर से अथवा सामने से गेंद का अवलोकन कीजिए। घूर्णन बिन्दु को यदि हम मध्य बिन्दु मानें तो यह गेंद एक क्षैतिज तल के अनुदिश इधर-उधर गति करती हुई प्रतीत होगी। विकल्पतः आप गेंद की परछार्ई वृत्त के तल के लंबवत् किसी दीवार पर भी देख सकते हैं। इस प्रक्रिया में हम जो कुछ अवलोकन करते हैं, वास्तव में वह हमारी दृष्टि की दिशा के अभिलंबवत् व्यास पर बॉल की गति होती है।

चित्र 13.9 किनारे से देखे गए एक समतल में बॉल की वृत्तीय गति सरल आवर्त गति है।
चित्र 13.10 इसी स्थिति को गणितीय रूप में वर्णन करता है। मान लीजिए कोई कण $\mathrm{P}$, त्रिज्या $A$ के एक वृत्त पर कोणीय चाल $\omega$ से एकसमानीय गति कर रहा है। घूमने की दिशा वामावर्त है। कण की प्रारंभिक ‘स्थिति सदिश’ अर्थात् $t=0$ पर सदिश OP , धनात्मक $x$ अक्ष के साथ कोण $\phi$ बनाता है। $t$ समय के बाद यह अगला कोण $\omega t$ पूरा करता है और इसकी ‘स्थिति सदिश’ +ve $x$-अक्ष के साथ एक कोण $\omega t+\phi$ बनाती है। अब $x$-अक्ष पर ‘स्थिति सदिश’ OP के प्रक्षेप पर विचार करें। यह $\mathrm{OP}^{\prime}$ होगा। जब कण $\mathrm{P}$ वृत्त पर गति करता है तो $x$ अक्ष पर $\mathrm{P}^{\prime}$ की स्थिति प्रदत्त की जाती है

चित्र 13.10
$$ x(t)=A \cos (\omega t+\phi) $$
जो कि SHM का पारिभाषिक समीकरण है। यह दर्शाता है कि यदि $\mathrm{P}$ किसी वृत्त पर एकसमानीय गति करता है तो इसका प्रक्षेप $\mathrm{P}^{\prime}$ वृत्त के व्यास पर सरल आवर्त गति करता है। कण $\mathrm{P}$ तथा वह वृत्त जिसपर यह गति करता है उसे क्रमशः संदर्भ कण तथा संदर्भ वृत्त कहते हैं।
$\mathrm{P}$ की गति के प्रक्षेप को हम किसी भी व्यास, जैसे कि $y$-अक्ष पर ले सकते हैं। इस स्थिति में $y$-अक्ष पर $\mathrm{P}^{\prime}$ का विस्थापन $y(t)$ होगा।
$$ y(t)=A \sin (\omega t+\phi) $$
यह भी एक SHM है जिसका आयाम $x$-अक्ष पर प्रक्षेप के समान ही है, लेकिन इसकी कला $\pi / 2$ से भिन्न है।
वर्तुल गति तथा SHM के बीच इस संबंध के बावजूद रैखिक सरल आवर्ती गति में किसी कण पर लगता हुआ बल किसी कण को एकसमान वर्तुल गति में रखने के लिए आवश्यक अभिकेन्द्रीय बल से काफी अलग है।
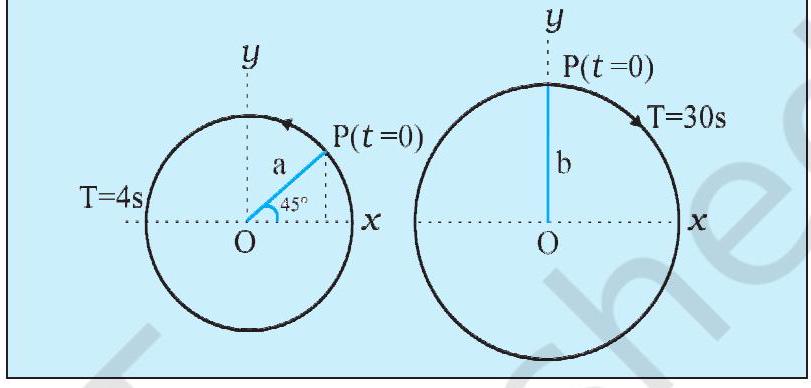
उदाहरण 13.4 नीचे दिये चित्र में दो वर्तुल गतियाँ दर्शायी गई हैं । इन चित्रों पर वृत्त की त्रिज्या, घूर्णन का आवर्तकाल आरंभिक स्थिति तथा घूर्णन की दिशा अंकित की गई है। प्रत्येक स्थिति में घूर्णी कण $\mathrm{P}$ के त्रिज्या सदिश के $x$-प्रक्षेप की सरल आवर्त गति प्राप्त कीजिए ।
हल
(a) $t=0$ पर, $\mathrm{OP} x$-अक्ष (की धनात्मक दिशा) से $45^{\circ}$ $=\pi / 4 \mathrm{rad}$ का कोण बनाता है। $t$ समय पश्चात् यह वामावर्त दिशा में $\frac{2 \pi}{T} t _{\mathrm{rad}}$ कोण पूरा करता है, तथा $x$-अक्ष से $\left(\frac{2 \pi}{T} t+\frac{\pi}{4}\right) \mathrm{rad}$ कोण बनाता है ।
समय $t$ पर $x$-अक्ष पर $\mathrm{OP}$ के प्रक्षेप इस प्रकार व्यक्त करते हैं :
$$x(t)=A \cos \left(\frac{2 \pi}{T} t+\frac{\pi}{4}\right)$$
$T=4 \mathrm{~s}$ के लिए
$$x(t)=A \cos \left(\frac{2 \pi}{4} t+\frac{\pi}{4}\right)$$
जो कि $A$ आयाम, $4 \mathrm{~s}$ आवर्तकाल तथा प्रारंभिक कला* $\frac{\pi}{4}$ की सरल आवर्त गति है ।
(b) इस स्थिति में $t=0$ पर, OP $x$-अक्ष से $90^{\circ}=\pi / 2$ का कोण बनाता है । यह दक्षिणावर्त दिशा में $\frac{2 \pi}{T} t$ कोण पूरा करता है, तथा $x$-अक्ष से $\left(\frac{\pi}{2}-\frac{2 \pi}{T} t\right)$ कोण बनाता है । समय $t$ पर $x$-अक्ष पर $\mathrm{OP}$ प्रक्षेप को इस प्रकार व्यक्त करते हैं :
$$ \begin{gathered} x(t)=B \cos \left(\frac{\pi}{2}-\frac{2 \pi}{T} t\right) \\ =B \sin \left(\frac{2 \pi}{T} t\right) \end{gathered} $$
$T=30 \mathrm{~s}$ के लिए,
$$ x(t)=B \sin \left(\frac{\pi}{15} t\right) $$
इसे इस प्रकार $x(t)=B \cos \left(\frac{\pi}{15} t-\frac{\pi}{2}\right)$ लिखकर इसकी समीकरण (13.4) से तुलना करने पर हमें यह ज्ञात होता है कि यह $B$ आयाम, $30 \mathrm{~s}$ आवर्तकाल तथा प्रारंभिक कला $-\frac{\pi}{2} \mathrm{rad}$ की सरल आवर्त गति को निरूपित करता है ।
कोण की प्राकृतिक इकाई रेडियन है जिसे त्रिज्या की चाप के अनुपात द्वारा परिभाषित करते हैं। कोण अदिश राशि है। जब हम $\pi$ को उसके बहुगुण या अपवर्तक लिखते हैं तो रेडियन इकाई का उल्लेख करना आवश्यक नहीं है। रेडियन और डिग्री के बीच रूपांतरण, मीटर, सेंटीमीटर या मील के बीच रूपांतरण के समरूप नहीं है। यदि किसी त्रिकोणमितीय फलन के कोणांक में इकाई नहीं दिया है तो मानना चाहिए कि इकाई रेडियन है। यदि कोण की इकाई डिग्री है तो उसको स्पष्टतः दर्शाना होगा। उदाहरण के लिए $\sin \left(15^{\circ}\right)$ का अर्थ है 15 डिग्री का $\sin$ । परन्तु $\sin (15)$ का तात्पर्य 15 रेडियन का $\sin$ है। आगे से ‘rad’ इकाई नहीं दर्शाया जाएगा। जब भी कोण का अंकिक मान बिना इकाई के दिया हुआ है तो इकाई वास्तव में रेडियन है।
13.5 सरल आवर्त गति में वेग तथा त्वरण
एकसमानीय वर्तुल गति करते हुए किसी कण की चाल इसकी कोणीय चाल गुणा वृत्त की त्रिज्या $A$ के बराबर होती है।
$$ \begin{equation*} v=\omega A \tag{13.8} \end{equation*} $$
किसी समय $t$ पर, वेग $\mathbf{v}$ की दिशा वृत्त के उस बिन्दु पर स्पर्शज्या के अनुदिश होती है जहाँ कण उस क्षण पर अवस्थित रहता है। चित्र 13.11 की ज्यामिति से यह स्पष्ट है कि समय $t$ पर प्रक्षेप कण $\mathrm{P}^{\prime}$ का वेग है
$$ \begin{equation*} v(t)=-\omega A \sin (\omega t+\phi) \tag{13.9} \end{equation*} $$

चित्र 13.11 कण $P^{\prime}$ का वेग $v(t)$ संदर्भ कण $P$ के वेग $\mathbf{v}$ का प्रक्षेप है ।
यहाँ ऋणात्मक चिह्न यह दर्शाता है कि $v(t)$ की दिशा $x$-अक्ष की धनात्मक दिशा के विपरीत है। समीकरण (13.9), सरल आवर्त गति करते हुए कण की तात्क्षणिक वेग प्रदत्त करता है, जहाँ विस्थापन समीकरण (13.4) से प्राप्त होता है। निस्संदेह इस समीकरण को हम बिना ज्यामितीय कोणांक के भी प्राप्त कर सकते हैं। इसके लिए सीधे समीकरण (13.4) को $t$ के सापेक्ष अवकलित करते हैं :
$$ \begin{equation*} v(t)=\frac{\mathrm{d}}{\mathrm{d} t} x(t) \tag{13.10} \end{equation*} $$
सरल आवर्त गति करते हुए कण के तात्क्षणिक त्वरण को प्राप्त करने के लिए संदर्भ वृत्त की विधि को इसी प्रकार प्रयोग में लाया जा सकता है। हमें ज्ञात है कि एकसमानीय वर्तुल गति में कण के अभिकेन्द्रीय त्वरण का परिमाण $v^{2} / A$ अथवा $\omega^{2} A$ है तथा यह केन्द्र की ओर निर्दिष्ट है, अर्थात इसकी दिशा $\mathrm{PO}$ की ओर है। प्रक्षेप कण $\mathrm{P}^{\prime}$ का तात्क्षणिक त्वरण तब होगा (चित्र 13.12 देखें)
$$ \begin{align*} a(t) & =-\omega^{2} A \cos (\omega t+\phi) \\ & =-\omega^{2} x(t) \tag{13.11} \end{align*} $$

चित्र 13.12 बिंदु $P^{\prime}$ का त्वरण $a(t)$, संदर्भ बिंदु $P$ के त्वरण $\mathbf{a}$ का प्रक्षेप होता है।
समीकरण (13.11) सरल आवर्त गति करते हुए कण का त्वरण व्यक्त करता है। इसी समीकरण को, समीकरण (13.9) से प्रदत्त वेग $v(t)$ को समय के सापेक्ष अवकलित करके सीधे प्राप्त किया जा सकता है:
$$ \begin{equation*} a(t)=\frac{\mathrm{d}}{\mathrm{d} t} v(t) \tag{13.12} \end{equation*} $$
समीकरण (13.11) से हम एक महत्त्वपूर्ण परिणाम पर ध्यान देते हैं कि सरल आवर्त गति में कण का त्वरण इसके विस्थापन के अनुक्रमानुपाती होता है। $x(t)>0$ के लिए $a(t)<0$ तथा $x(t)<0$ के लिए $a(t)>0$ होता है। अतः $-A$ तथा $A$ के बीच $x$ का मान कुछ भी हो, त्वरण $\mathrm{a}(\mathrm{t})$ हमेशा केन्द्र की ओर निर्दिष्ट रहता है।
सरलता के लिए हम $\phi=0$ रख कर $x(t), v(t)$ और $a(t)$ के व्यंजक को लिखते हैं
$x(t)=A \cos \omega t, v(t)=-\omega A \sin \omega t, a(t)=-\omega^{2} A \cos \omega t$ संगत आलेख को चित्र 13.13 में दर्शाया गया है। सभी राशियाँ समय के साथ ज्यावक्रीय विचरण करती हैं; केवल उनकी उच्चिष्ठ (maxima) में अन्तर होता है तथा उनके आलेखों में कलाओं की भिन्नता होती है। $x,-A$ तथा $A$ के मध्य विचरण करता है; $v(t),-\omega A$ तथा $\omega A$ के मध्य विचरण करता है एवं $a(t),-\omega^{2} A$ तथा $\omega^{2} A$ के मध्य विचरण करता है। विस्थापन आलेख के सापेक्ष, वेग आलेख की कला में $\pi / 2$ का अंतर है तथा त्वरण आलेख की कला में $\pi$ का अंतर है।
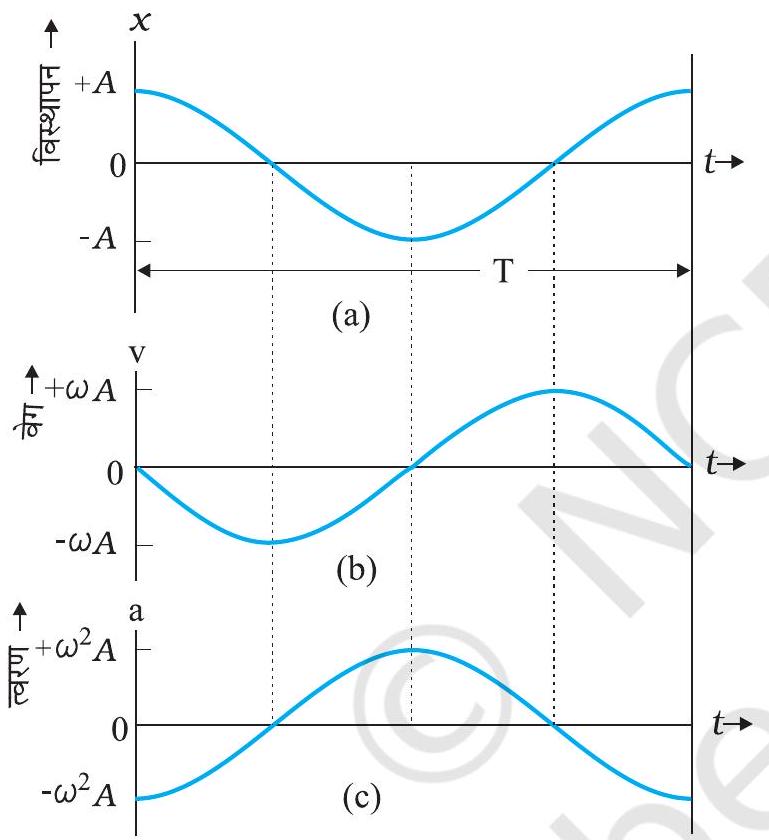
चित्र 13.13 सरल आवर्त गति में किसी कण का विस्थापन, वेग तथा त्वरण का आवर्तकाल $T$ समान होता है, लेकिन उनकी कलाओं में भिन्नता होती है।
उदाहरण 13.5: कोई पिंड निम्नलिखित समीकरण के अनुसार सरल आवर्त गति से दोलन करता है,
$$ x=5 \cos [2 \pi t+\pi / 4] . $$
$t=1.5 \mathrm{~s}$ पर, पिंड का (a) विस्थापन, (b) वेग तथा (c) त्वरण परिकलित कीजिए।
हल पिंड की कोणीय आवृत्ति $\omega=2 \pi \mathrm{s}^{-1}$ तथा इसका आवर्तकाल $T=1 \mathrm{~s}$
$t=1.5 \mathrm{~s}$ पर
(a) विस्थापन $=(5.0 \mathrm{~m}) \cos \left[\left(2 \pi \mathrm{s}^{-1}\right) \times 1.5 \mathrm{~s}+\frac{\pi}{4}\right]$
$$ \begin{aligned} & =(5.0 \mathrm{~m}) \cos [(3 \pi+\pi / 4)] \\ & =-5.0 \times 0.707 \mathrm{~m} \\ & =-3.535 \mathrm{~m} \end{aligned} $$
(b) समीकरण (13.9) का उपयोग करने पर पिंड का वेग
$=-(5.0 \mathrm{~m})\left(2 \pi \mathrm{s}^{-1}\right) \sin \left[\left(2 \pi \mathrm{s}^{-1}\right) \times 1.5 \mathrm{~s}\right.$ $+\pi / 4]$
$=-(5.0 \mathrm{~m})\left(2 \pi \mathrm{s}^{-1}\right) \sin [(3 \pi+\pi / 4)]$
$=10 \pi \times 0.707 \mathrm{~m} \mathrm{~s}^{-1}$
$=22 \mathrm{~m} \mathrm{~s}^{-1}$
(c) समीकरण (13.10) का उपयोग करने पर पिंड का त्वरण
$ \begin{aligned} & =-\left(2 \pi \mathrm{s}^{-1}\right)^{2} \times \text { विस्थापन } \\ & =-\left(2 \pi \mathrm{s}^{-1}\right)^{2} \times(-3.535 \mathrm{~m}) \\ & =130 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $
13.6 सरल आवर्त गति के लिए बल का नियम
न्यूटन की गति के दूसरे नियम तथा आवर्त गति करते किसी कण के लिए त्वरण के व्यंजक (समीकरण 13.11) प्रयोग करने पर
$$ \begin{align*} F(t) & =m a \\ & =-m \omega^{2} x(t) \end{align*} $$
$$ \text{अथवा,} \quad F(t)=-k x(t) \tag{13.13}$$
$$ \text{यहाँ} \quad k=m \omega^{2} \tag{13.14a}$$
$$ \text{अथवा,} \quad \omega=\sqrt{\frac{k}{m}} \tag{13.14b}$$
त्वरण की तरह, बल हमेशा माध्य स्थिति की ओर निर्दिष्ट रहता है - इसलिए यह सरल आवर्त गति में प्रत्यानयन बल कहलाता है। अब तक की गई चर्चाओं को संक्षिप्त करने पर हम पाते हैं कि सरल आवर्त गति को दो प्रकार से परिभाषित किया जा सकता है, या तो विस्थापन के लिए समीकरण (13.4) द्वारा अथवा समीकरण (13.13) द्वारा जो कि बल के नियम प्रदान करता है। समीकरण (13.4) से समीकरण (13.13) प्राप्त करने के लिए हमें इसे दो बार अवकलित करना पड़ा। इसी प्रकार बल के नियम, समीकरण (13.13) को दो बार समाकलित करने पर हमें वापस समीकरण (13.4) प्राप्त हो सकता है।
ध्यान दीजिए कि समीकरण (13.13) में बल $x(t)$ के रैखिकीय समानुपाती है। अतः इस तरह के बल के प्रभाव से दोलन करते हुए किसी कण को रैखिक आवर्ती दोलक कहते हैं। वास्तव में, बल के व्यंजक में $x^{2}, x^{3}$ आदि के समानुपाती कुछ पद हो सकते हैं। अतः इन्हें अरैखिक दोलक कहते हैं।
उदाहरण 13.6 कमानी स्थिरांक $k$ की दो सर्वसम कमानियाँ $M$ संहति के किसी गुटके तथा स्थिर आधारों से चित्र 13.14 में दर्शाए गए अनुसार जुड़ी हुई हैं। यह दर्शाइए कि जब गुटके को अपनी साम्यावस्था की स्थिति से किसी ओर विस्थापित किया जाता है, तब यह सरल आवर्त गति करता है। दोलन का आवर्तकाल ज्ञात कीजिए ।

चित्र 13.14
हल मान लीजिए गुटके को अपनी साम्यावस्था की स्थिति से दाईं ओर $x$ दूरी तक विस्थापित किया जाता है। इसे चित्र 13.15 में दिखाया गया है। इस स्थिति में बार् ओर की कमानी $x$ लंबाई द्वारा दीर्घित हो जाती है तथा दार्ई ओर की कमानी भी उतनी ही लंबाई द्वारा संपीडित हो जाती है । तब गुटके पर कार्यरत बल

चित्र 13.15
$F _{1}=-k x$ (कमानी द्वारा बाईं ओर आरोपित बल, जो गुटके को माध्य स्थिति की ओर खींचने का प्रयास करता है।)
$F _{2}=-k x$ (कमानी द्वारा दाईं ओर आरोपित बल, जो गुटके को माध्य स्थिति की ओर धकेलने का प्रयास करता है।)
तब गुटके पर आरोपित नेट बल,
$ F=-2 k x $
अतः, गुटके पर आरोपित बल विस्थापन के अनुक्रमानुपाती तथा माध्य-स्थिति की ओर निर्दिष्ट होता है; इसलिए, गुटके की गति सरल आवर्त गति है। इसमें दोलन का आवर्तकाल,
$ T=2 \pi \sqrt{\frac{m}{2 k}} \text { है । } $
13.7 सरल आवर्त गति में ऊर्जा
सरल आवर्त गति करते हुए कण की स्थितिज तथा गतिज ऊर्जाएँ दोनों शून्य तथा अपने अधिकतम परिमाण के बीच विचरण करती हैं।
अनुभाग 13.5 में हमने देखा है कि सरल आवर्त गति करते किसी कण का वेग समय का आवर्ती फलन होता है। विस्थापन की चरम स्थितियों में यह शून्य होता है । अतः ऐसे कण की गतिज ऊर्जा (K), जिसे हम इस प्रकार परिभाषित करते हैं,
$ \begin{align*} K & =\frac{1}{2} m v^{2} \end{align*} $
$ \begin{align*} & =\frac{1}{2} m \omega^{2} A^{2} \sin ^{2}(\omega t+\phi) \end{align*} $
$ \begin{align*} & =\frac{1}{2} k A^{2} \sin ^{2}(\omega t+\phi) \tag{13.15} \end{align*} $
भी समय का आवर्ती फलन होती है जिसका परिमाण विस्थापन अधिकतम होने पर शून्य तथा कण के माध्य स्थिति पर होने पर अधिकतम होता है । ध्यान दीजिए, चूँकि गतिज ऊर्जा $K$ में, $v$ के चिह्न का कोई अर्थ नहीं होता, अतः $K$ का आवर्तकाल $T / 2$ है।
सरल आवर्त गति करने वाले किसी कण की स्थितिज ऊर्जा कितनी होती है ? अध्याय 5 में हमने देखा है कि स्थितिज ऊर्जा की संकल्पना केवल संरक्षी बलों के लिए ही होती है । कमानी बल $F=-k x$ एक संरक्षी बल है जिससे स्थितिज ऊर्जा संयुक्त होती है ।
$$ \begin{equation*} U=\frac{1}{2} k x^{2} \tag{13.16} \end{equation*} $$
अतः सरल आवर्त गति करते किसी कण की स्थितिज ऊर्जा,
$ \begin{align*} & U(x)=\frac{1}{2} k x^{2} \end{align*} $
$ \begin{align*} & =\frac{1}{2} k A^{2} \cos ^{2}(\omega t+\phi) \tag{13.17} \end{align*} $
इस प्रकार, सरल आवर्त गति करते किसी कण की स्थितिज ऊर्जा भी आवर्ती होती है जिसका आवर्तकाल $T / 2$ होता है, यह ऊर्जा माध्य स्थिति में शून्य तथा चरम विस्थापनों पर अधिकतम होती है ।
अतः समीकरणों (13.15) तथा (13.17) से हमें निकाय की कुल ऊर्जा $E$, प्राप्त होती है,
$ E=U+K $
$ \begin{aligned} & =\frac{1}{2} k A^{2} \cos ^{2}(\omega t+\phi)+\frac{1}{2} k A^{2} \sin ^{2}(\omega t+\phi) \\ & =\frac{1}{2} k A^{2}\left[\cos ^{2}(\omega t+\phi)+\sin ^{2}(\omega t+\phi)\right] \end{aligned} $
त्रिकोणमिती की सामान्य तादात्मक को प्रयोग करने पर कोष्ठक में दी गई राशि का मान एक प्राप्त होता है। अत:
$$ \begin{equation*} E=\frac{1}{2} k A^{2} \tag{13.18} \end{equation*} $$
जैसा कि संरक्षी बलों के अधीन गतियों के लिए आशा की जाती है किसी भी सरल आवर्ती दोलक की कुल यांत्रिक ऊर्जा कालाश्रित नहीं होती । किसी रैखिक सरल आवर्ती दोलक की गतिज तथा स्थितिज ऊर्जाओं की समय और विस्थापन पर निर्भरता चित्र 13.16 में दर्शायी गई है ।
चित्र 13.16 गतिज ऊर्जा, स्थितिज ऊर्जा तथा कुल ऊर्जा समय के फलन के रूप में [(a) में दर्शित] तथा सरल आवर्त गति करते हुए कण का विस्थापन [(b) में दर्शित]। गतिज ऊर्जा तथा स्थितिज ऊर्जा दोनों आवर्तकाल $T / 2$ के पश्चात पुनरावृत्ति करते हैं। $t$ तथा $x$ के सभी मानों के लिए कुल ऊर्जा नियत रहती है।
ध्यान दीजिए कि सरल आवर्त गति में स्थितिज तथा गतिज दोनों ऊर्जाएँ चित्र 13.16 में हमेशा धनात्मक मानी गई हैं। निस्सन्देह गतिज ऊर्जा कभी ऋणात्मक नहीं हो सकती, क्योंकि यह चाल के वर्ग के समानुपाती होती है। स्थितिज ऊर्जा के समीकरण में गुप्त नियतांक के चयन के कारण स्थितिज ऊर्जा धनात्मक होती है। गतिज तथा स्थितिज दोनों ऊर्जाएँ SHM के प्रत्येक आवर्तकाल में दो बार अपनी चरम स्थिति को प्राप्त करती हैं। $x=0$ के लिए, ऊर्जा गतिज है; चरम स्थिति $x= \pm A$ पर यह पूरे तौर पर स्थितिज ऊर्जा है। इन सीमाओं के बीच गति करते हुए, स्थितिज ऊर्जा के घटने से गतिज ऊर्जा बढ़ती है तथा गतिज ऊर्जा के घटने से स्थितिज ऊर्जा बढ़ती है।
उदाहरण 13.7 $1 \mathrm{~kg}$ संहति के किसी गुटके को एक कमानी से बाँधा गया है । कमानी का कमानी स्थिरांक $50 \mathrm{~N} \mathrm{~m}^{-1}$ है । गुटके को उसकी साम्यावस्था की स्थिति $x=0$ से $t=0$ पर किसी घर्षणहीन पृष्ठ पर कुछ दूरी $x=10 \mathrm{~cm}$ तक खींचा जाता है । जब गुटका अपनी माध्य-स्थिति से $5 \mathrm{~cm}$ दूर है, तब उसकी गतिज, स्थितिज तथा कुल ऊर्जाएँ परिकलित कीजिए ।
हल
गुटका सरल आवर्त गति करता है । समीकरण [13.14(b)] से इसकी कोणीय आवृत्ति
$ \begin{aligned} \omega & =\sqrt{k / m} \\ & =\sqrt{\frac{50 \mathrm{~N} \mathrm{~m}}{1 \mathrm{~kg}}}\\ \\ & =7.07 \mathrm{rad} \mathrm{s}^{-1} \text { होगी, }\\ \end{aligned} $
तब किसी समय $t$ पर इसका विस्थापन
$$ x(t)=0.1 \cos (7.07 t) \text { होगा । } $$
अतः, जब कण अपनी माध्य स्थिति से $5 \mathrm{~cm}$ दूर है, तब
$$ 0.05=0.1 \cos (7.07 t) $$
अथवा $\cos (7.07 t)=0.5$,
अतः, $\sin (7.07 t)=\frac{\sqrt{3}}{2}=0.866$
तब गुटके का $x=5 \mathrm{~cm}$ पर वेग
$$ \begin{aligned} & =0.1 \times 7.070 .866 \mathrm{~m} \mathrm{~s}^{-1} \\ & =0.61 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
अतः, गुटके की गतिज ऊर्जा
$$ \begin{aligned} & =\frac{1}{2} m v^{2} \\ & =1 / 2\left[1 \mathrm{~kg} \times\left(0.6123 \mathrm{~m} \mathrm{~s}^{-1}\right)^{2}\right] \\ & =0.19 \mathrm{~J} \end{aligned} $$
तथा गुटके की स्थितिज ऊर्जा
$$=\frac{1}{2} k x^{2}$$ $ \begin{gathered} =\frac{1}{2}\left(50 \mathrm{~N} \mathrm{~m}^{-1} \times 0.05 \times 0.05 \mathrm{~m}\right) \\ =0.0625 \mathrm{~J} \end{gathered} $
$\therefore x=5 \mathrm{~cm}$ पर गुटके की कुल ऊर्जा
$$ \begin{aligned} & =(0.19+0.0625) \mathrm{J} \\ & =0.25 \mathrm{~J} \end{aligned} $$
हम यह भी जानते हैं कि अधिकतम विस्थापन पर, गतिज ऊर्जा शून्य होती है, अतः निकाय की कुल ऊर्जा स्थितिज ऊर्जा के बराबर होती है। अत: निकाय की कुल ऊर्जा,
$$ \begin{aligned} & =\frac{1}{2}\left(50 \mathrm{~N} \mathrm{~m}^{-1} \times 0.1 \mathrm{~m} \times 0.1 \mathrm{~m}\right) \\ & =0.25 \mathrm{~J} \end{aligned} $$
यह ऊर्जा $5 \mathrm{~cm}$ विस्थापन पर दोनों ऊर्जाओं के योग के बराबर ही है । यह ऊर्जा संरक्षण सिद्धांत के अनुकूल है।
13.8.1 सरल लोलक
यह कहा जाता है कि गैलीलियो ने किसी चर्च में एक दोलायमान झाड़फानूस का आवर्तकाल अपनी नाड़ी की स्पंद गति द्वारा मापा था । उसने यह निष्कर्ष निकाला कि झाड़फानूस की गति आवर्ती है। यह निकाय लोलक का ही एक प्रकार होता है । लगभग 1 मीटर लंबे न खिंचने वाले धागे को लेकर उसके एक सिरे से पत्थर का टुकड़ा बाँधकर आप भी अपना एक लोलक बना सकते हैं। अपने लोलक को किसी उचित टेक से बाँधकर इस प्रकार लटकाइए कि वह स्वतंत्रतापूर्वक दोलन कर सके । पत्थर के टुकड़े को कम दूरी तक विस्थापित करके छोड़ दीजिए । पत्थर इधर-उधर गति करने लगता है। पत्थर की यह गति आवर्ती होती है जिसका आवर्तकाल लगभग 2 सेकंड होता है।

चित्र 13.17 (a) माध्य स्थिति के सापेक्ष दोलन करता कोई सरल लोलक, (b) त्रिज्य बल $T-m g \cos \theta$ अभिकेन्द्र बल प्रदान करता है परंतु धुराग्र के सापेक्ष इसका कोई बल-आघूर्ण नहीं होता। स्पर्श रेखीय बल $m g \sin \theta$ प्रत्यानयन बल प्रदान करता है।
हम यह स्थापित करेंगे कि मध्यमान स्थिति से लघु विस्थापनों के लिए इस लोलक की आवर्त गति सरल आवर्त गति होती है। किसी ऐसे सरल लोलक पर विचार कीजिए जिसमें $m$ द्रव्यमान का कोई लघु आमाप का गोलक $L$ लम्बाई के द्रव्यमानहीन तथा न खिंचने योग्य डोरी के एक सिरे से बंधा हो। डोरी का दूसरा सिरा किसी दृढ़ टेक से जुड़ा है। गोलक इस ऊर्ध्वाधर दृढ़ टेक से होकर जाने वाली रेखा के अनुदिश तल में दोलन करता है। यह व्यवस्था चित्र 13.17(a) द्वारा दर्शाई गई है। चित्र 13.17(b) में दोलक पर कार्यरत बल प्रदर्शित किए गए हैं जो एक प्रकार का बल-निर्देशक आरेख है।
माना कि डोरी ऊर्ध्वाधर से $\theta$ कोण बनाती है। जब गोलक माध्य स्थिति में होता है तो $\theta=0$
गोलक पर केवल दो बल कार्यरत हैं : डोरी की लंबाई के अनुदिश तनाव $\mathrm{T}$ तथा गुरुत्व के कारण ऊर्ध्वाधर बल $(=m g)$ । हम बल $m g$ का वियोजन डोरी के अनुदिश घटक $m g \cos \theta$ तथा उसके लंबवत् $m g \sin \theta$ के रूप में कर सकते हैं। चूँकि गोलक की गति $L$ त्रिज्या के किसी वृत्त के अनुदिश है जिसका केन्द्र धुराग्र बिन्दु पर स्थित है, अतः गोलक का कोई त्रिज्य त्वरण $\left(\omega^{2} L\right)$ तथा साथ ही स्पर्शेरीय त्वरण होगा। स्पर्शरेखीय त्वरण का कारण वृत्त के चाप के अनुरूप गति का एकसमान न होना है। त्रिज्य त्वरण नेट त्रिज्य बल $T-m g \cos \theta$ के कारण होता है जबकि स्पर्शरेखीय त्वरण $m g \sin \theta$ के कारण उत्पन्न होता है। धुराग्र के सापेक्ष बल आघूर्ण पर विचार करना अधिक सुविधाजनक होता है क्योंकि तब त्रिज्य बल का आघूर्ण शून्य हो जाता है। इस प्रकार आधार के सापेक्ष बल आघूर्ण $\tau$ बल के स्पर्शरेखीय घटक द्वारा ही पूर्णतया प्राप्त होता है।
$$ \begin{equation*} \tau=-L(m g \sin \theta) \tag{13.19} \end{equation*} $$
यह एक प्रत्यानयन बल आघूर्ण है जो विस्थापन के परिणाम को कम करने का प्रयास करता है; इसी कारण इसे ॠणात्मक चिह्न द्वारा व्यक्त किया गया है। घूर्णी गति के लिए न्यूटन के नियम के अनुसार
$$ \begin{equation*} \tau=I \alpha \tag{13.20} \end{equation*} $$
यहाँ $I$ धुराग्र बिंदु के परितः लोलक का घूर्णी जड़त्व है तथा $\alpha$ उसी बिंदु के परितः कोणीय त्वरण है । इस प्रकार
$$ \begin{equation*} I \alpha=-m g L \sin \theta \tag{13.21} \end{equation*} $$
अथवा
$$ \begin{equation*} \alpha=-\frac{m g L}{I} \sin \theta \tag{13.22} \end{equation*} $$
यदि हम यह मानें कि विस्थापन $\theta$ छोटा है, तो समीकरण (13.22) को सरल बना सकते हैं । हम जानते हैं कि $\sin \theta$ को इस प्रकार व्यक्त किया जा सकता है,
$$ \begin{equation*} \sin \theta=\theta-\frac{\theta^{3}}{3 !}+\frac{\theta^{5}}{5 !}-\cdots \cdots \tag{13.23} \end{equation*} $$
यहाँ $\theta$ रेडियन में है।
अब यदि $\theta$ छोटा है, तो $\sin \theta$ का सन्निकटन $\theta$ द्वारा किया जा सकता है। ऐसी परिस्थिति के समीकरण (13.22) को इस प्रकार भी लिख सकते हैं,
$$ \begin{equation*} \alpha=-\frac{m g L}{I} \theta \tag{13.24} \end{equation*} $$
सारणी 13.1 में हमने कोण $\theta$ को अंशों में, इसके तुल्यांक रेडियनों में, तथा फलन $\sin \theta$ के मान सूचीबद्ध किए हैं । सारणी से यह देखा जा सकता है कि $\theta$ के 20 अंश तक बड़े मानों के लिए $\sin \theta$ के मान लगभग वही होते हैं जैसे $\theta$ को रेडियनों में व्यक्त करने पर मिलते हैं
सारणी $13.1 \sin \theta$ कोण $\theta$ के फलन के रूप में
| $\theta$ (अंशों में ) | $\theta$ (रेडियनों में ) | $\sin \theta$ |
|---|---|---|
| 0 | 0 | 0 |
| 5 | 0.087 | 0.087 |
| 10 | 0.174 | 0.174 |
| 15 | 0.262 | 0.259 |
| 20 | 0.349 | 0.342 |
गणितीय रूप में समीकरण (13.24) समीकरण (13.11) के तुल्य है, अंतर केवल यह है कि यहाँ चर राशि कोणीय त्वरण है। अतः हमने यह सिद्ध कर दिया है कि $\theta$ के लघु मानों के लिए गोलक की गति सरल आवर्त गति है। समीकरण (13.24) तथा समीकरण (13.11) से हम यह देखते हैं कि
$$ \omega=\sqrt{\frac{m g L}{I}} $$
तथा लोलक का आवर्तकाल
$$ \begin{equation*} T=2 \pi \sqrt{\frac{I}{m g L}} \tag{13.25} \end{equation*} $$
अब क्योंकि लोलक की डोरी द्रव्यहीन है, अतः जड़त्व आघूर्ण $I$ केवल $m L^{2}$ के तुल्य होगा। इससे हमें सरल लोलक के आवर्त काल के लिए सुपरिचित सूत्र मिल जाता है
$$ \begin{equation*} T=2 \pi \sqrt{\frac{L}{g}} \tag{13.26} \end{equation*} $$
उदाहरण 13.8 उस सरल लोलक की लंबाई क्या है, जो हर सेकंड के बाद टिक करता है ?
हल समीकरण (13.26) से किसी सरल लोलक का आवर्तकाल,
$$ T=2 \pi \sqrt{\frac{L}{g}} $$
इस संबंध से हमें प्राप्त होता है,
$$ L=\frac{g T^{2}}{4 \pi^{2}} $$
हर एक सेकंड के बाद टिक करने वाले सरल लोलक का आवर्तकाल $T, 2 \mathrm{~s}$ होता है । अतः $g=9.8 \mathrm{~m} \mathrm{~s}^{-2}$ तथा $T=2 \mathrm{~s}$ के लिए सरल लोलक की लंबाई
$$ \begin{aligned} & L=\frac{9.8\left(\mathrm{~m} \mathrm{~s}^{-2}\right) \times 4\left(\mathrm{~s}^{2}\right)}{4 \pi^{2}} \ & =1 \mathrm{~m} \end{aligned} $$
सारांश
1. वह गति जो स्वयं को दोहराती है आवर्ती गति कहलाती है,
2. एक दोलन अथवा चक्र को पूरा करने के लिए आवश्यक समय $T$ को आवर्तकाल कहते हैं । यह आवृत्ति से इस प्रकार संबंधित है,
$$ T=\frac{1}{v} $$
किसी आवर्ती अथवा दोलनी गति की आवृत्ति उसके द्वारा 1 सेकंड में पूरे किए गए दोलनों की संख्या होती है । SI मात्रक पद्धति में इसे हर्ट्ज़ में मापा जाता है;
$$ 1 \text { हर्ट्ज़ }=1 \mathrm{~Hz}=1 \text { दोलन प्रति सेकंड }=1 \mathrm{~s}^{-1} $$
3. सरल आवर्त गति में, किसी कण का उसकी साम्यावस्था की स्थिति से विस्थापन $x(t)$ इस प्रकार व्यक्त किया जाता है,
$$ \left.x(t)=x _{\mathrm{m}} \cos (\omega t+\phi) \quad \text { ( विस्थापन }\right) $$
यहाँ $x _{m}$ विस्थापन का आयाम $(\omega t+\phi)$ गति की कला, तथा $\phi$ कला स्थिरांक है । कोणीय आवृत्ति $\omega$ गति के आवर्तकाल तथा आवृत्ति से इस प्रकार संबंधित होती है
$$ \omega=\frac{2 \pi}{T}=2 \pi \nu(\text { कोणीय आवृत्ति }) $$
4. सरल आवर्त गति, एकसमान वर्तुल गति के उस वृत्त के व्यास पर प्रक्षेप होती है, जिस पर गति हो रही है ।
5. सरल आवर्त गति के समय कण के वेग तथा त्वरण को समय $t$ के फलन के रूप में इस प्रकार व्यक्त करते हैं,
$$ \begin{array}{rlr} v(t) & =-\omega A \sin (\omega t+\phi) & \text { (velocity), } \\ \\ a(t) & =-\omega^{2} A \cos (\omega t+\phi) & \\ \\ & =-\omega^{2} x(t) & \text { (त्वरण), } \end{array} $$
समयकालिक क्रिया और सरल आवर्त गति द्वारा हम वेग और गति को इस प्रकार देख सकते हैं।
6. सरल आवर्त गति किसी कण की वह गति होती है जिसमें उस कण पर कोई ऐसा बल आरोपित रहता है, जो कण के विस्थापन के अनुक्रमानुपाती, तथा सदैव गति के केंद्र की ओर निर्दिष्ट होता है ।
7. सरल आवर्त गति करते किसी कण में, किसी भी क्षण, गतिज ऊर्जा $K=\frac{1}{2} m v^{2}$ तथा स्थितिज ऊर्जा $\mathrm{U}=\frac{1}{2} k x^{2}$ होती है । यदि कोई घर्षण न हो, तो निकाय की कुल यांत्रिक ऊर्जा, $E=K+U$ सदैव ही अचर रहती है यद्यपि $K$ और $U$ परिवर्तित होते हैं ।
8. $m$ द्रव्यमान का कोई कण जो हुक के नियम के अनुसार लगे प्रत्यानयन बल $F=-k x$ के प्रभाव में दोलन करता है,
$$ \begin{aligned} \omega & =\sqrt{\frac{k}{m}} \text { (कोणीय आवृत्ति) } \\ \text { तथा } \quad T & =2 \pi \sqrt{\frac{m}{k}} \text { (आवर्तकाल) } \end{aligned} $$
ऐसे निकाय को रैखिक दोलक भी कहते हैं ।
9. लघु कोणों में दोलन करते सरल लोलक की गति सन्निकट सरल आवर्त गति होती है । इसका आवर्तकाल,
$$ T=2 \pi \sqrt{\frac{L}{g}} $$
| भौतिक राशि | प्रतीक | विमाएँ | मात्रक | टिप्पणी |
|---|---|---|---|---|
| आवर्तकाल | $T$ | $[\mathrm{~T}]$ | $\mathrm{s}$ | गति की स्वयं पुनरावृत्ति के लिए न्यूनतम समय |
| आवृत्ति | $f$ या $v$ | $\left[\mathrm{~T}^{-1}\right]$ | $\mathrm{s}^{-1}$ | $v=\frac{1}{T}$ |
| कोणीय आवृत्ति | $\omega$ | $\left[\mathrm{T}^{-1}\right]$ | $\mathrm{s}^{-1}$ | $=2 \pi v$ |
| कला नियतांक | $\phi$ | विमाहीन | रेडियन | सरल आवर्त गति में विस्थापन की कला का आरंभिक मान |
| बल नियतांक | $k$ | $\left[\mathrm{MT}^{-2}\right]$ | $\mathrm{N} \mathrm{m}^{-1}$ | सरल आवर्त गति में $\qquad F=-k x$ |
विचारणीय विषय
1. आवर्तकाल $T$ वह न्यूनतम समय होता है जिसके पश्चात् गति की स्वयं पुनरावृत्ति होती है। इस प्रकार, समय अंतराल $n T$ के पश्चात् गति की स्वयं पुनरावृत्ति होती है, यहाँ $n$ कोई पूर्णांक है ।
2. प्रत्येक आवर्ती गति सरल आवर्त गति नहीं होती। केवल वही आवर्ती गति जो बल-नियम $F=-k x$ द्वारा नियंत्रित होती है, सरल आवर्त गति होती है ।
3. वर्तुल गति व्युत्क्रम-वर्ग नियम बल (जैसे ग्रहीय गति में) तथा द्विविमा में सरल आवर्त बल $-m \omega^{2} r$ के कारण उत्पन्न हो सकती है। बाद के प्रकरण में, गति की कलाएँ, दो लंबवत् दिशाओं $(x$ तथा $y)$ में $\pi / 2 \mathrm{rad}$ द्वारा भिन्न होनी चाहिए। इस प्रकार, कोई कण जिसकी आरंभिक स्थिति $(0, a)$ तथा वेग $(\omega A, 0)$ है $-m \omega^{2} r$ बल आरोपित किए जाने पर $A$ त्रिज्या के वृत्त में एकसमान वर्तुल गति करेगा।
4. $\omega$ के किसी दिए गए मान की रैखिक सरल आवर्त गति के लिए दो आरंभिक शर्तें आवश्यक हैं और ये शर्तें गति को पूर्णतः निर्धारित करने के लिए पर्याप्त हैं। ये आवश्यक शर्तें हो सकती हैं (i) आरंभिक स्थिति तथा आरंभिक वेग, अथवा (ii) आयाम तथा कला, अथवा (iii) ऊर्जा तथा कला।
5. उपरोक्त बिंदु (4) से, दिए गए आयाम अथवा ऊर्जा गति की कला का निर्धारण आरंभिक स्थिति अथवा आरंभिक वेग द्वारा किया जाता है।
6. यादृच्छिक आयामों तथा कलाओं वाली दो सरल आवर्त गतियों का संयोजन व्यापक रूप में आवर्ती नहीं होता। यह केवल तभी आवर्ती होता है जब एक गति की आवृत्ति दूसरी गति की आवृत्ति की पूर्णांक गुणज हो। तथापि, किसी आवर्ती गति को सदैव ही उपयुक्त आयामों की अनंत सरल आवर्त गतियों के रूप में व्यक्त किया जा सकता है।
7. सरल आवर्त गति का आवर्तकाल आयाम अथवा ऊर्जा अथवा कला नियतांक पर निर्भर नहीं करता। गुरुत्वाकर्षण के अधीन ग्रहीय कक्षों के आवर्तकाल इसके विपरीत हैं (केप्लर का तृतीय नियम)।
8. किसी सरल लोलक की गति लघु कोणीय विस्थापन के लिए ही सरल आवर्त गति होती है।
9. किसी कण की गति यदि सरल आवर्त गति है, तो उसके विस्थापन को निम्न रूपों में से किसी एक रूप में व्यक्त किया जाना चाहिए :
$$ \begin{aligned} & x=A \cos \omega t+B \sin \omega t \\ & x=A \cos (\omega t+\alpha) ; x=B \sin (\omega t+\beta) \end{aligned} $$
ये तीनों रूप पूर्णतः समतुल्य हैं (किसी भी एक रूप को अन्य दो रूपों के पदों में व्यक्त किया जा सकता है।)
अभ्यास
13.1 नीचे दिए गए उदाहरणों में कौन आवर्ती गति को निरूपित करता है ?
(i) किसी तैराक द्वारा नदी के एक तट से दूसरे तट तक जाना और अपनी एक वापसी यात्रा पूरी करना ।
(ii) किसी स्वतंत्रतापूर्वक लटकाए गए दंड चुंबक को उसकी $\mathrm{N}-\mathrm{S}$ दिशा से विस्थापित कर छोड़ देना।
(iii) अपने द्रव्यमान केंद्र के परितः घूर्णी गति करता कोई हाइड्रोजन अणु।
(iv) किसी कमान से छोड़ा गया तीर ।
Show Answer
#Content Missing13.2 नीचे दिए गए उदाहरणों में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परंतु सरल आवर्त गति नहीं निरूपित करते हैं ?
(i) पृथ्वी की अपने अक्ष के परितः घूर्णन गति ।
(ii) किसी U-नली में दोलायमान पारे के स्तंभ की गति।
(iii) किसी चिकने वक्रीय कटोरे के भीतर एक बॉल बेयरिंग की गति जब उसे निम्नतम बिंदु से कुछ ऊपर के बिंदु से मुक्त रूप से छोड़ा जाए।
(iv) किसी बहुपरमाणुक अणु की अपनी साम्यावस्था की स्थिति के परितः व्यापक कंपन।
Show Answer
#Content Missing13.3 चित्र 13.18 में किसी कण की रैखिक गति के लिए चार $x$ - $t$ आरेख दिए गए हैं। इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है ? उस गति का आवर्तकाल क्या है (आवर्ती गति वाली गति का)।

चित्र 13.18
Show Answer
#Content Missing13.4 नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परंतु सरल आवर्त गति नहीं, तथा (c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए : ( $\omega$ कोई धनात्मक अचर है।)
(a) $\sin \omega t-\cos \omega t$
(b) $\sin ^{3} \omega t$
(c) $3 \cos \left(\frac{\pi}{4}-2 \omega t\right)$
(d) $\cos \omega t+\cos 3 \omega t+\cos 5 \omega t$
(e) $\exp \left(-\omega^{2} t^{2}\right)$
(f) $1+\omega t+\omega^{2} t^{2}$
Show Answer
#Content Missing13.5 कोई कण एक दूसरे से $10 \mathrm{~cm}$ दूरी पर स्थित दो बिंदुओं $\mathrm{A}$ तथा $\mathrm{B}$ के बीच रैखिक सरल आवर्त गति कर रहा है। $\mathrm{A}$ से $\mathrm{B}$ की ओर की दिशा को धनात्मक दिशा मानकर वेग, त्वरण तथा कण पर लगे बल के चिह्न ज्ञात कीजिए जबकि यह कण
(a) $\mathrm{A}$ सिरे पर है,
(b) $\mathrm{B}$ सिरे पर है,
(c) $\mathrm{A}$ की ओर जाते हुए $\mathrm{AB}$ के मध्य बिंदु पर है,
(d) $\mathrm{A}$ की ओर जाते हुए $\mathrm{B}$ से $2 \mathrm{~cm}$ दूर है,
(e) $\mathrm{B}$ की ओर जाते हुए $\mathrm{A}$ से $3 \mathrm{~cm}$ दूर है, तथा
(f) $\mathrm{A}$ की ओर जाते हुए $\mathrm{B}$ से $4 \mathrm{~cm}$ दूर है ।
Show Answer
#Content Missing13.6 नीचे दिए गए किसी कण के त्वरण $a$ तथा विस्थापन $x$ के बीच संबंधों में से किससे सरल आवर्त गति संबद्ध है :
(a) $a=0.7 x$
(b) $a=-200 x^{2}$
(c) $a=-10 x$
(d) $a=100 x^{3}$
Show Answer
#Content Missing13.7 सरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है,
$$ x(t)=A \cos (\omega t+\phi) $$
यदि कण की आरंभिक $(t=0)$ स्थिति $1 \mathrm{~cm}$ तथा उसका आरंभिक वेग $\pi \mathrm{cm} \mathrm{s}^{-1}$ है, तो कण का आयाम तथा आरंभिक कला कोण क्या है ? कण की कोणीय आवृत्ति $\pi \mathrm{s}^{-1}$ है । यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या $(\sin )$ फलन चुनें; $x=B \sin (\omega t+\alpha)$, तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा ?
Show Answer
#Content Missing13.8 किसी कमानीदार तुला का पैमाना 0 से $50 \mathrm{~kg}$ तक अंकित है और पैमाने की लंबाई $20 \mathrm{~cm}$ है। इस तुला से लटकाया गया कोई पिण्ड, जब विस्थापित करके मुक्त किया जाता है, $0.6 \mathrm{~s}$ के आवर्तकाल से दोलन करता है । पिंड का भार कितना है ?
Show Answer
#Content Missing13.9 $1200 \mathrm{~N} \mathrm{~m}^{-1}$ कमानी-स्थिरांक की कोई कमानी चित्र 13.19 में दर्शाए अनुसार किसी क्षैतिज मेज से जड़ी है। कमानी के मुक्त सिरे से $3 \mathrm{~kg}$ द्रव्यमान का कोई पिण्ड जुड़ा है । इस पिण्ड को एक ओर $2.0 \mathrm{~cm}$ दूरी तक खींच कर मुक्त किया जाता है,

चित्र 13.19
(i) पिण्ड के दोलन की आवृत्ति,
(ii) पिण्ड का अधिकतम त्वरण, तथा
(iii) पिण्ड की अधिकतम चाल ज्ञात कीजिए।
Show Answer
#Content Missing13.10 अभ्यास 13.9 में, मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति $x=0$ है तथा बाएँ से दाएँ की दिशा $x$-अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन $x$ को समय के फलन के रूप मे दर्शाइए, जबकि विराम घड़ी को आरंभ $(t=0)$ करते समय पिण्ड,
(a) अपनी माध्य स्थिति,
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम संपीडन की स्थिति पर है ।
सरल आवर्त गति के लिए ये फलन एक दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न हैं ?
Show Answer
#Content Missing13.11 चित्र 13.20 में दिए गए दो आरेख दो वर्तुल गतियों के तदनुरूपी हैं। प्रत्येक आरेख पर वृत्त की त्रिज्य, परिक्रमण-काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शायी गई है। प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य-सदिश के $x$-अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति ज्ञात कीजिए।

चित्र 13.20
Show Answer
#Content Missing13.12 नीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनुरूपी निर्देश वृत्त का आरेख खींचिए। घूर्णी कण की आरंभिक $(t=0)$ स्थिति, वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए। सुगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त लीजिए। ( $x$ को $\mathrm{cm}$ में तथा $t$ को $\mathrm{s}$ में लीजिए।)
(a) $x=-2 \sin (3 t+\pi / 3)$
(b) $x=\cos (\pi / 6-t)$
(c) $x=3 \sin (2 \pi t+\pi / 4)$
(d) $x=2 \cos \pi t$
Show Answer
#Content Missing13.13 चित्र 13.21(a) में $k$ बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढ़ आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान $m$ जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल $\mathbf{F}$ आरोपित करने से कमानी तन जाती है । चित्र $13.21(\mathrm{~b})$ में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान $m$ जुड़ा दर्शाया गया है । कमानी के दोनों सिरों को चित्र 13.21 में समान बल $\mathbf{F}$ द्वारा तानित किया गया है ।

चित्र 13.21
(a) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है ?
(b) यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए ।
Show Answer
#Content Missing13.14 किसी रेलगाड़ी के इंजन के सिलिंडर हैड में पिस्टन का स्ट्रोक (आयाम का दो गुना) $1.0 \mathrm{~m}$ का है । यदि पिस्टन $200 \mathrm{rad} / \mathrm{min}$ की कोणीय आवृत्ति से सरल आवर्त गति करता है, तो उसकी अधिकतम चाल कितनी है ?
Show Answer
#Content Missing13.15 चंद्रमा के पृष्ठ पर गुरुत्वीय त्वरण $1.7 \mathrm{~m} \mathrm{~s}^{-2}$ है । यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल $3.5 \mathrm{~s}$ है, तो उसका चंद्रमा के पृष्ठ पर आवर्तकाल कितना होगा ? (पृथ्वी के पृष्ठ पर $g=9.8 \mathrm{~m} \mathrm{~s}^{-2}$ )
Show Answer
#Content Missing13.16 किसी कार की छत से $l$ लंबाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान $M$ है, लटकाया गया है । कार $R$ त्रिज्या की वृत्तीय पथ पर एकसमान चाल $v$ से गतिमान है । यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है, तो इसका आवर्तकाल क्या होगा ?
Show Answer
#Content Missing13.17 आधार क्षेत्रफल $A$ तथा ऊँचाई $h$ के एक कॉर्क का बेलनाकार टुकड़ा $\rho _{l}$ घनत्व के किसी द्रव में तैर रहा है । कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल
$T=2 \pi \sqrt{\frac{h \rho}{\rho _{1} g}}$ है ।
यहाँ $\rho$ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए)।
Show Answer
#Content Missing13.18 पारे से भरी किसी $U$ नली का एक सिरा किसी चूषण पंप से जुड़ा है, तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है । दोनों स्तंभों में कुछ दाबांतर बनाए रखा जाता है । यह दर्शाइए कि जब चूषण पंप को हटा देते हैं, तब $U$ नली में पारे का स्तंभ सरल आवर्त गति करता है ।





