अध्याय 02 सरल रेखा में गति
2.1 भूमिका
विश्व की प्रत्येक वस्तु प्रत्यक्ष या अप्रत्यक्ष रूप से गतिमान रहती है । हमारा चलना, दौड़ना, साइकिल सवारी आदि दैनिक जीवन में दिखाई देने वाली क्रियाएँ गति के कुछ उदाहरण हैं। इतना ही नहीं, निद्रावस्था में भी हमारे फेफड़ों में वायु का प्रवेश एवं निष्कासन तथा हमारी धमनियों एवं शिराओं में रुधिर का संचरण होता रहता है । हम पेड़ों से गिरते हुए पत्तों को तथा बाँध से बहते हुए पानी को देखते हैं । मोटरगाड़ी और वायुयान यात्रियों को एक स्थान से दूसरे स्थान को ले जाते हैं । पृथ्वी 24 घंटे में एक बार अपनी अक्ष के परितः घूर्णन करती है तथा वर्ष में एक बार सूर्य की परिक्रमा पूरी करती है । सूर्य अपने ग्रहों सहित हमारी आकाशगंगा नामक मंदाकिनी में विचरण करता है, तथा जो स्वयं भी स्थानीय मंदाकिनियों के समूह में गति करती है ।
इस प्रकार समय के सापेक्ष वस्तु की स्थिति में परिवर्तन को गति कहते हैं। समय के साथ स्थिति कैसे परिवर्तित होती है ? इस अध्याय में हम गति के बारे में पढ़ेंगे । इसके लिए हमें वेग तथा त्वरण की धारणा को समझना होगा । इस अध्याय में हम अपना अध्ययन वस्तु के एक सरल रेखा के अनुदिश गति तक ही सीमित रखेंगे । इस प्रकार की गति को सरल रेखीय गति भी कहते हैं । एकसमान त्वरित सरल रेखीय गति के लिए कुछ सरल समीकरण प्राप्त किए जा सकते हैं। अंततः गति की आपेक्षिक प्रकृति को समझने के लिए हम आपेक्षिक गति की धारणा प्रस्तुत करेंगे ।
इस अध्ययन में हम सभी गतिमान वस्तुओं को अतिसूक्ष्म मानकर बिंदु रूप में निरूपित करेंगे । यह सन्निकटन तब तक मान्य होता है जब तक वस्तु का आकार निश्चित समय अंतराल में वस्तु द्वारा चली गई दूरी की अपेक्षा पर्याप्त रूप से कम होता है । वास्तविक जीवन में बहुत-सी स्थितियों में वस्तुओं के आमाप (साइज़) की उपेक्षा की जा सकती है और बिना अधिक त्रुटि के उन्हें एक बिंदु-वस्तु माना जा सकता है । शुद्धगतिकी में, हम वस्तु की गति के कारणों पर ध्यान न देकर केवल उसकी गति का ही अध्ययन करते हैं। इस अध्याय एवं अगले अध्याय में विभिन्न प्रकार की गतियों का वर्णन किया गया है । इन गतियों के कारणों का अध्ययन हम पाँचवें अध्याय में करेंगे ।
2.2 तात्क्षणिक वेग एवं चाल
जैसा कि हम पढ़ चुके हैं कि औसत वेग से हमें यह ज्ञात होता है कि कोई वस्तु किसी दिए गए समय अंतराल में किस गति से चल रही है, किन्तु इससे यह पता नहीं चल पाता कि इस समय अंतराल के भिन्न-भिन्न क्षणों पर वह किस गति से चल रही है। अतः किसी क्षण $t$ पर वेग के लिए हम तात्क्षणिक वेग या केवल वेग $v$ को परिभाषित करते हैं । गतिमान वस्तु का तात्क्षणिक वेग उसके औसत वेग के बराबर होगा यदि उसके दो समयों $(t$ तथा $t+\Delta t)$ के बीच का अंतराल $(\Delta t)$ अनन्तः सूक्ष्म हो । गणितीय विधि से हम इस कथन को निम्न प्रकार से व्यक्त करते हैं
$\begin{aligned} v & =\lim _{\Delta \mathrm{t} \rightarrow 0} \frac{\Delta x}{\Delta t} \ & =\frac{\mathrm{d} x}{\mathrm{~d} t}\end{aligned}$
यहाँ प्रतीक $\lim _{\Delta \rightarrow 0}$ का तात्पर्य उसके दायीं ओर स्थित राशि (जैसे $\frac{\Delta x}{\Delta t}$ ) का वह मान है जो $\Delta t$ के मान को शून्य की ओर $(\Delta t \rightarrow 0)$ प्रवृत्त करने पर प्राप्त होगा। कलन गणित की भाषा में समीकरण में दायीं ओर की राशि $\left(\frac{\mathrm{d} x}{\mathrm{~d} t}\right) x$ का $t$ के सापेक्ष अवकलन गुणांक है। यह गुणांक उस क्षण पर वस्तु की स्थिति परिवर्तन की दर होती है।
किसी क्षण पर वस्तु का वेग निकालने के लिए हम समीकरण (2.1a) का उपयोग कर सकते हैं । इसके लिए ग्राफिक या गणितीय विधि को प्रयोग में लाते हैं। मान लीजिए कि हम गतिमान कार का वेग $t=4 \mathrm{~s}$ (बिंदु $\mathrm{P}$ ) पर निकालना चाहते हैं। पहले हम $t=4 \mathrm{~s}$ को केंद्र में रखकर $\Delta t$ को $2 \mathrm{~s}$ लें। औसत वेग की परिभाषा के अनुसार सरल रेखा $\mathrm{P} _{1} \mathrm{P} _{2}$ (चित्र 2.1) की प्रवणता $3 \mathrm{~s}$ से $5 \mathrm{~s}$ के अंतराल में वस्तु के औसत वेग को व्यक्त करेगी ।
चित्र 2.1 स्थिति-समय ग्राफ से वेग ज्ञात करना $। t=4 \mathrm{~s}$ पर वेग उस क्षण पर ग्राफ की स्पर्श रेखा की प्रवणता है।
अब हम $\Delta t$ का मान $2 \mathrm{~s}$ से घटाकर $1 \mathrm{~s}$ कर देते हैं तो $\mathrm{P} _{1} \mathrm{P} _{2}$ रेखा $\mathrm{O} _{1} \mathrm{O} _{2}$ हो जाती है और इसकी प्रवणता $3.5 \mathrm{~s}$ से $4.5 \mathrm{~s}$ अंतराल में औसत वेग का मान देगी । अंततः सीमांत मान $\Delta t \rightarrow 0$ की परिस्थिति में रेखा $\mathrm{P} _{1} \mathrm{P} _{2}$ स्थिति-समय वक्र के बिंदु $\mathrm{P}$ पर स्पर्श रेखा हो जाती है । इस प्रकार $t=4 \mathrm{~s}$ क्षण पर कार का वेग उस बिंदु पर खींची गई स्पर्श रेखा की प्रवणता के बराबर होगा । यद्यपि ग्राफिक विधि से इसे प्रदर्शित करना कुछ कठिन है तथापि यदि इसके लिए हम गणितीय विधि का उपयोग करें तो सीमांत प्रक्रिया आसानी से समझी जा सकती है । चित्र 2.1 में खींचे गए ग्राफ के लिए $x=0.8 t^{3}$ है । सारणी 2.1 में $t=4 \mathrm{~s}$ को केंद्र में रखकर $\Delta t=2.0 \mathrm{~s}, 1.0 \mathrm{~s}$, $0.5 \mathrm{~s}, 0.1 \mathrm{~s}$ तथा $0.01 \mathrm{~s}$ के लिए $\Delta x / \Delta t$ के मूल्यों को दर्शाया गया है । दूसरे और तीसरे कॉलम में $t _{1}(=t-\Delta t / 2)$ तथा $t _{2}(=t-\Delta t / 2)$ और चौथे एवं पाँचवें कॉलम में $x$ के तदनुरूप मानों अर्थात $x\left(t _{1}\right)=0.08 t _{1}^{3}$ तथा $x\left(t _{2}\right)=0.03 t^{3}$ को दिखलाया गया है । छठे कॉलम में अंतर $\Delta x=x\left(t _{2}\right)-x\left(t _{1}\right)$ को तथा अंतिम कॉलम में $\Delta x$ व $\Delta t$ के अनुपात को व्यक्त किया गया है । यह अनुपात प्रथम कॉलम में अंकित $\Delta t$ के भिन्न-भिन्न मानों के संगत औसत वेग का मान है ।
सारणी 2.1 $t=4 \mathrm{~s}$ के लिए $\Delta x / \Delta t$ का सीमांत मान
| $\Delta t$ $(\mathbf{s})$ |
$\boldsymbol{t} _{\boldsymbol{1}}$ $(\mathrm{s})$ |
$\boldsymbol{t} _{2}$ $(\mathbf{s})$ |
$\boldsymbol{x}\left(\boldsymbol{t} _{\boldsymbol{1}}\right)$ $(\mathbf{m})$ |
$\boldsymbol{x}\left(\boldsymbol{t} _{2}\right)$ $(\mathbf{m})$ |
$\Delta \boldsymbol{x}$ $(\mathbf{m})$ |
$\Delta \boldsymbol{\Delta} / \Delta \boldsymbol{t}$ $\left(\mathrm{m} \mathrm{s}^{-1}\right)$ |
|---|---|---|---|---|---|---|
| 2.0 | 3.0 | 5.0 | 2.16 | 10.0 | 7.84 | 3.92 |
| 1.0 | 3.5 | 4.5 | 3.43 | 7.29 | 3.86 | 3.86 |
| 0.5 | 3.75 | 4.25 | 4.21875 | 6.14125 | 1.9225 | 3.845 |
| 0.1 | 3.95 | 4.05 | 4.93039 | 5.31441 | 0.38402 | 3.8402 |
| 0.01 | 3.995 | 4.005 | 5.100824 | 5.139224 | 0.0384 | 3.8400 |
सारणी 2.1 से स्पष्ट है कि जैसे-जैसे $\Delta t$ का मान $2.0 \mathrm{~s}$ से घटाते-घटाते $0.01 \mathrm{~s}$ करते हैं तो औसत वेग अंततः सीमांत मान $3.84 \mathrm{~ms}^{-1}$ के बराबर हो जाता है जो $t=4 \mathrm{~s}$ पर कार का वेग है अर्थात $t=4 \mathrm{~s}$ पर $d x / d t$ का मान । इस प्रकार गति के हर क्षण के लिए हम कार का वेग निकाल सकते हैं ।
यहाँ यह बात ध्यान देने योग्य है कि वस्तु का तात्क्षणिक वेग निकालने के लिए ग्राफिक विधि सदैव सुविधाजनक नहीं होती है । इस विधि (ग्राफिक विधि) में हम गतिमान वस्तु के स्थिति-समय ग्राफ को सावधानीपूर्वक खींचते हैं तथा $\Delta t$ को उत्तरोत्तर कम करते हुए वस्तु के औसत वेग $(\bar{v})$ की गणना करते जाते हैं । भिन्न-भिन्न क्षणों पर वस्तु का वेग निकालना तब बहुत आसान हो जाता है जब विभिन्न समयों पर हमारे पास वस्तु की स्थिति के पर्याप्त आँकड़े उपलब्ध हों अथवा वस्तु की स्थिति का समय के फलन के रूप में हमारे पास यथार्थ व्यंजक उपलब्ध हो। ऐसी स्थिति में उपलब्ध आँकड़ों का उपयोग करते हुए समय अंतराल $\Delta t$ को क्रमशः सूक्ष्म करते हुए $\Delta x / \Delta t$ का मान निकालते जाएँगे और अंततः सारणी 2.1 में दर्शाई गई विधि के अनुसार $\Delta x /$ $\Delta t$ का सीमांत मान प्राप्त कर लेंगे । अन्यथा किसी दिए गए व्यंजक के लिए अवकल गणित का प्रयोग करके गतिमान वस्तु के भिन्न-भिन्न क्षणों के लिए $d x / d t$ की गणना कर लेंगे जैसा कि उदाहरण 2.1 में बताया गया है ।
उदाहरण 2.1 $x$-अक्ष के अनुदिश किसी गतिमान वस्तु की स्थिति निम्नलिखित सूत्र से व्यक्त की जाती है : $x=a+b t^{2}$ । यहाँ $a=8.5 \mathrm{~m}, b=2.5 \mathrm{~m} \mathrm{~s}^{-2}$ तथा समय $t$ को सेकंड में व्यक्त किया गया है । $t=0 \mathrm{~s}$ तथा $t=2.0 \mathrm{~s}$ क्षणों पर वस्तु का वेग क्या होगा ? $t=2.0 \mathrm{~s}$ तथा $t=4.0 \mathrm{~s}$ के मध्य के समय अंतराल में वस्तु का औसत वेग क्या होगा ?
हल अवकल गणित की पद्धति के अनुसार वस्तु का वेग
$$ v=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{\mathrm{d}}{\mathrm{d} t}\left(a+b t^{2}\right)=2 b t=5.0 t \mathrm{~m} \mathrm{~s}^{-1} $$
$t=0 \mathrm{~s}$ क्षण के लिए $v=0 \mathrm{~m} / \mathrm{s}$, तथा $t=2.0 \mathrm{~s}$ समय पर, $V=10 \mathrm{~m} \mathrm{~s}^{-1}$
औसत वेग $=\frac{x\left(t _{2}\right)-x\left(t _{1}\right)}{t _{2}-t _{1}}=\frac{x(4.0)-x(2.0)}{4.0-2.0}$
$$ \begin{aligned} & =\frac{(a+16 b)-(a+4 b)}{2.0}=6.0 b \\ & =6.02 .5=15 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
ध्यान दीजिए कि एकसमान गति में हर समय ( तात्क्षणिक) वेग का वही मान होता है जो औसत वेग का होता है।
तात्क्षणिक चाल या केवल चाल गतिमान वस्तु के वेग का परिमाण है । उदाहरण के तौर पर, वेग $+24.0 \mathrm{~m} \mathrm{~s}^{-1}$ तथा $-24.0 \mathrm{~m} \mathrm{~s}^{-1}$ दोनों में प्रत्येक का परिमाण $24.0 \mathrm{~m} \mathrm{~s}^{-1}$ होगा। यहाँ यह तथ्य ध्यान में रखना है कि जहाँ किसी सीमित समय अंतराल में वस्तु की औसत चाल उसके औसत वेग के परिमाण के या तो बराबर होती है या उससे अधिक होती है वहीं किसी क्षण पर वस्तु की तात्क्षणिक चाल उस क्षण पर उसके तात्क्षणिक वेग के परिमाण के बराबर होती है । ऐसा क्यों होता है ?
2.3 त्वरण
सामान्यतः वस्तु की गति की अवधि में उसके वेग में परिवर्तन होता रहता है । वेग में हो रहे इस परिवर्तन को कैसे व्यक्त करें। वेग में हो रहे इस परिवर्तन को समय के सापेक्ष व्यक्त करना चाहिए या दूरी के सापेक्ष ? यह समस्या गैलीलियो के समय भी थी। गैलीलियो ने पहले सोचा कि वेग में हो रहे परिवर्तन की इस दर को दूरी के सापेक्ष व्यक्त किया जा सकता है परंतु जब उन्होंने मुक्त रूप से गिरती हुई तथा नत समतल पर गतिमान वस्तुओं की गति का विधिवत् अध्ययन किया तो उन्होंने पाया कि समय के सापेक्ष वेग परिवर्तन की दर का मान मुक्त रूप से गिरती हुई वस्तुओं के लिए, स्थिर रहता है जबकि दूरी के सापेक्ष वस्तु का वेग परिवर्तन स्थिर नहीं रहता वरन जैसे-जैसे गिरती हुई वस्तु की दूरी बढ़ती जाती है वैसे-वैसे यह मान घटता जाता है। इस अध्ययन ने त्वरण की वर्तमान धारणा को जन्म दिया जिसके अनुसार त्वरण को हम समय के सापेक्ष वेग परिवर्तन के रूप में परिभाषित करते हैं ।
जब किसी वस्तु का वेग समय के सापेक्ष बदलता है तो हम कहते हैं कि उसमें त्वरण हो रहा है । वेग में परिवर्तन तथा तत्संबंधित समय अंतराल के अनुपात को हम औसत त्वरण कहते हैं । इसे $\bar{a}$ से प्रदर्शित करते हैं :
$$ \begin{equation*} \bar{a}=\frac{v _{2}-v _{1}}{t _{2}-t _{1}}=\frac{\Delta v}{\Delta t} \tag{2.2} \end{equation*} $$
यहां $t _{1}, t _{2}$ क्षणों पर वस्तु का वेग क्रमशः $v _{1}$ तथा $v _{2}$ है । यह एकांक समय में वेग में औसत परिवर्तन होता है । त्वरण का $\mathrm{SI}$ मात्रक $\mathrm{m} \mathrm{s}^{-2}$ है ।
वेग-समय $(v-t)$ ग्राफ से हम वस्तु का औसत त्वरण निकाल सकते हैं । यह इस प्रकार के ग्राफ में उस सरल रेखा की प्रवणता के बराबर होता है जो बिंदु $\left(v _{2}, t _{2}\right)$ को बिंदु $\left(v _{1}, t _{1}\right)$ से जोड़ती है ।
तात्क्षणिक त्वरण : जिस प्रकार हमने पूर्व में तात्क्षणिक वेग की व्याख्या की है, उसी प्रकार हम तात्क्षणिक त्वरण को भी परिभाषित करते हैं। वस्तु के तात्क्षणिक त्वरण को $a$ से चिह्नित करते हैं, अर्थात
$$ \begin{equation*} a=\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{\mathrm{d} v}{\mathrm{~d} t} \tag{2.3} \end{equation*} $$
$v-t$ ग्राफ में किसी क्षण वस्तु का त्वरण उस क्षण वक्र पर खींची गई स्पर्श रेखा की प्रवणता के बराबर होता है ।
चूँकि वेग एक सदिश राशि है जिसमें दिशा एवं परिमाण दोनों होते हैं अतएव वेग परिवर्तन में इनमें से कोई एक अथवा दोनों निहित हो सकते हैं । अतः या तो चाल (परिमाण) में परिवर्तन, दिशा में परिवर्तन अथवा इन दोनों में परिवर्तन से त्वरण का उद्भव हो सकता है। वेग के समान ही त्वरण भी धनात्मक, ऋणात्मक अथवा शून्य हो सकता है। इसी प्रकार के त्वरण संबंधी स्थिति-समय ग्राफों को चित्रों 2.2 (a), 2.2 (b) तथा 2.2 (c) में दर्शाया गया है । चित्रों से स्पष्ट है कि धनात्मक त्वरण के लिए $x-t$ ग्राफ ऊपर की ओर वक्रित है किन्तु ॠणात्मक त्वरण के लिए ग्राफ नीचे की ओर वक्रित है । शून्य त्वरण के लिए $x-t$ ग्राफ एक सरल रेखा है ।

चित्र 2.2 ऐसी गति के लिए स्थिति-समय ग्राफ जिसके लिए (a) त्वरण धनात्मक है, (b) त्वरण ऋणात्मक है तथा (c) त्वरण शून्य है ।
यद्यपि गतिमान वस्तु का त्वरण समय के साथ-साथ बदल सकता है, परंतु सुविधा के लिए इस अध्याय में गति संबंधी हमारा अध्ययन मात्र स्थिर त्वरण तक ही सीमित रहेगा । ऐसी स्थिति में औसत त्वरण $\bar{a}$ का मान गति की अवधि में स्थिर त्वरण के मान के बराबर होगा । यदि क्षण $t=0$ पर वस्तु का वेग $v _{0}$ तथा $t$ क्षण पर उसका वेग $v$ हो, तो त्वरण
$a=\bar{a}=\frac{v-v _{0}}{t-0}$ होगा ।
$$ \begin{equation*} \text { अतएव, } v=v _{0}+a t \tag{2.4} \end{equation*} $$
अब हम यह देखेंगे कि कुछ सरल उदाहरणों में वेग-समय ग्राफ कैसा दिखलाई देता है । चित्र 2.3 में स्थिर त्वरण के लिए चार अलग-अलग स्थितियों में $v-t$ ग्राफ दिखाए गए हैं:

चित्र 2.3 स्थिर त्वरण के साथ गतिमान वस्तु का वेग-समय ग्राफ (a) धनात्मक त्वरण से धनात्मक दिशा में गति, (b) ऋणात्मक त्वरण से धनात्मक दिशा में गति, (c) ॠणात्मक त्वरण से ॠणात्मक दिशा में गति, (d) ॠणात्मक त्वरण के साथ वस्तु की गति जो समय $t _{1}$ पर दिशा बदलती है । 0 से $t _{1}$ समयावधि में यह धनात्मक $x$ की दिशा में गति करती है जबकि $t _{1}$ व $t _{2}$ के मध्य वह विपरीत दिशा में गतिमान है ।
(a) कोई वस्तु धनात्मक दिशा में धनात्मक त्वरण से गतिमान है।
(b) कोई वस्तु धनात्मक दिशा में ऋणात्मक त्वरण से गतिमान है।
(c) कोई वस्तु ऋणात्मक दिशा में ऋणात्मक त्वरण से गतिमान है ।
(d) कोई वस्तु पहले $t _{1}$ समय तक धनात्मक दिशा में चलती है और फिर ऋणात्मक दिशा में ऋणात्मक त्वरण के साथ गतिमान है ।
किसी गतिमान वस्तु के वेग-समय ग्राफ का एक महत्त्वपूर्ण लक्षण है कि $v-t$ ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु का विस्थापन व्यक्त करता है। इस कथन की सामान्य उपपत्ति के लिए अवकल गणित की आवश्यकता पड़ती है तथापि सुगमता के लिए एक स्थिर वेग $u$ से गतिमान वस्तु पर विचार करके इस कथन की सत्यता प्रमाणित कर सकते हैं। इसका वेग-समय ग्राफ चित्र 2.4 में दिखाया गया है ।

चित्र $2.4 \mathrm{~V}$ - $t$ ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु द्वारा निश्चित समय अंतराल में विस्थापन व्यक्त करता है।
चित्र में $v$ - $t$ वक्र समय अक्ष के समांतर एक सरल रेखा है । $t=0$ से $t=T$ के मध्य इस रेखा के अंतर्गत आने वाला क्षेत्रफल उस आयत के क्षेत्रफल के बराबर है जिसकी ऊँचाई $u$ तथा आधार $T$ है । अतएव क्षेत्रफल $=u \times T=u T$, जो इस समय में वस्तु के विस्थापन को व्यक्त करता है । कोई क्षेत्रफल दूरी के बराबर कैसे हो सकता है ? सोचिए ! दोनों निर्देशांक अक्षों के अनुदिश जो राशियाँ अंकित की गई हैं, यदि आप उनकी विमाओं पर ध्यान देंगे तो आपको इस प्रश्न का उत्तर मिल जाएगा।
ध्यान दीजिए कि इस अध्याय में अनेक स्थानों पर खींचे गए $x-t, v-t$ तथा $a-t$ ग्राफों में कुछ बिंदुओं पर तीक्ष्ण मोड़ हैं। इसका आशय यह है कि दिए गए फलनों का इन बिंदुओं पर अवकलन नहीं निकाला जा सकता । परंतु किसी वास्तविक परिस्थिति में सभी ग्राफ निष्कोण वक्र होंगे और उनके सभी बिंदुओं पर फलनों का अवकलन प्राप्त किया जा सकता है।
इसका अभिप्राय है कि वेग तथा त्वरण किसी क्षण सहसा नहीं बदल सकते। परिवर्तन सदैव सतत होता है।
2.4 एकसमान त्वरण से गतिमान वस्तु का शुद्धगतिकी
संबंधी समीकरणअब हम एकसमान त्वरण ’ $a$ ’ से गतिमान वस्तु के लिए कुछ गणितीय समीकरण व्युत्पन्न कर सकते हैं जो पाँचों राशियों को किसी प्रकार एक दूसरे से संबंधित करते हैं । ये राशियाँ हैं: विस्थापन $(x)$, लिया गया समय $(t), t=0$ समय पर वस्तु का प्रारंभिक वेग $(v)$, समय $t$ बीत जाने पर अंतिम वेग $(v)$, तथा त्वरण (a)। हम पहले ही $v _{o}$ और $V$ के मध्य एक समीकरण (2.4) प्राप्त कर चुके हैं जिसमें एकसमान त्वरण $a$ तथा समय $t$ निहित हैं । यह समीकरण है :
$$ \begin{equation*} v=v _{o}+a t \tag{2.4} \end{equation*} $$
इस समीकरण को चित्र 2.5 में ग्राफ के रूप में निरूपित किया गया है । इस वक्र के अंतर्गत आने वाला क्षेत्रफल : 0 से $t$ समय के बीच का क्षेत्रफल $=$ त्रिभुज $\mathrm{ABC}$ का क्षेत्रफल + आयत $\mathrm{OACD}$ का क्षेत्रफल
$$ =\frac{1}{2}\left(\mathrm{~V}-V _{0}\right) t+v _{0} t $$

चित्र 2.5 एकसमान त्वरण से गतिमान वस्तु के लिए $v-t$ वक्र के नीचे का क्षेत्रफल ।
जैसे कि पहले स्पष्ट किया जा चुका है, $v-t$ ग्राफ के अंतर्गत आने वाला क्षेत्रफल वस्तु का विस्थापन होता है। अतः वस्तु का विस्थापन $x$ होगा :
$$ \begin{equation*} x=\frac{1}{2}\left(v-v _{0}\right) t+v _{0} t \tag{2.5} \end{equation*} $$
परंतु $\quad\quad v-V _{0}=a t$
अत: $\quad x=\frac{1}{2} a t^{2}+v _{O} t$
अथवा $\quad\quad x=v _{0} t+\frac{1}{2} a t^{2}$
समीकरण (2.5) को हम निम्न प्रकार भी लिख सकते हैं
$$ \begin{align*} X & =\frac{V+v _{0}}{2} t \\ & =\bar{v} \cdot t \tag{2.7a} \\ \bar{v} & =\frac{v+v _{0}}{2} \text { ( मात्र स्थिर त्वरण के लिए ) } \tag{2.7b} \end{align*} \quad $$
समीकरण (2.7a) तथा (2.7b) का अभिप्राय है कि वस्तु का विस्थापन $X$ माध्य वेग $\bar{V}$ से होता है जो प्रारंभिक एवं अंतिम वेगों के समांतर माध्य के बराबर होता है ।
समीकरण (2.4) से $t=\left(v-v _{0}\right) / a$ । यह मान समीकरण (2.7a) में रखने पर
$$ \begin{align*} x & =\bar{v} t=\frac{v+v _{0}}{2} \cdot \frac{v-v _{0}}{a}=\frac{v^{2}-v _{0}^{2}}{2 a} \\ v^{2} & =v _{0}^{2}+2 a x \tag{2.8} \end{align*} $$
यदि हम समीकरण (2.4) से $t$ का मान समीकरण (2.6) में रख दें तो भी उपरोक्त समीकरण को प्राप्त किया जा सकता है। इस प्रकार पांचों राशियों $V _{0}, V, a, t$ तथा $x$ के बीच संबंध स्थापित करनेवाले हमें तीन महत्त्वपूर्ण समीकरण प्राप्त हुए-
$$ \begin{align*} v & =v _{0}+a t \\ x & =v _{0} t+\frac{1}{2} a t^{2} \\ v^{2} & =v _{0}^{2}+2 a x \tag{2.9a} \end{align*} $$
ये सभी एकसमान त्वरित सरल रेखीय गति के शुद्धगतिक समीकरण हैं ।
व्यंजक (2.9a) में जो समीकरण दिए गए हैं, उसकी व्युत्पत्ति के लिए हमने माना है कि क्षण $t=0$ पर वस्तु की स्थिति 0 है (अर्थात् $x=0$ ) । परंतु यदि हम यह मान लें कि क्षण $t=$ 0 पर वस्तु की स्थिति शून्य न हो, वरन् अशून्य यानी $x _{0}$ हो तो समीकरण (2.9a) और व्यापक समीकरण में रूपांतरित हो जाएगी (यदि हम $x$ के स्थान पर $x-X _{O}$ लिखें):
$$ \begin{align*} v & =v _{0}+a t \\ x & =x _{0}+v _{0} t+\frac{1}{2} a t^{2} \tag{2.9b} \\ v^{2} & =v _{0}^{2}+2 a\left(x-x _{0}\right) \tag{2.9c} \end{align*} $$
उदाहरण 2.2 कलन-विधि का उपयोग कर एकसमान त्वरण के लिए शुद्धगतिक समीकरण प्राप्त कीजिए।
हल परिभाषा से
$$ \begin{gathered} a=\frac{\mathrm{d} v}{\mathrm{~d} t} \\ \mathrm{~d} v=a \mathrm{~d} t \end{gathered} $$
दोनों पक्षों के समाकलन से
$$ \begin{gathered} \int _{v _{0}}^{v} \mathrm{~d} v=\int _{0}^{t} a \mathrm{~d} t \\ =a \int _{0}^{t} \mathrm{~d} t \quad(a \text { अचर है }) \\ v-v _{0}=a t \\ v=v _{0}+a t \end{gathered} $$
पुन: $\quad v=\frac{\mathrm{d} x}{\mathrm{~d} t}$
दोनों पक्षों के समाकलन से $$ \mathrm{d} x=v \mathrm{~d} t $$ $$ \begin{aligned} \int_{x_0}^x \mathrm{~d} x=\int_0^t v \mathrm{~d} t & =\int_0^t\left(v_0+a t\right) \mathrm{d} t \\ x-x_0 & =v_0 t+\frac{1}{2} a t^2 \\ x & =x_0+v_0 t+\frac{1}{2} a t^2 \end{aligned} $$
हम लिख सकते हैं :
$$ a=\frac{\mathrm{d} v}{\mathrm{~d} t}=\frac{\mathrm{d} v}{\mathrm{~d} x} \frac{\mathrm{d} x}{\mathrm{~d} t}=v \frac{\mathrm{d} v}{\mathrm{~d} x} $$ अथवा, $v \mathrm{~d} v=a \mathrm{~d} x$
दोनों पक्षों के समाकलन से
$$ \begin{aligned} & \int _{v _{0}}^{v} v \mathrm{~d} v=\int _{x _{0}}^{x} a \mathrm{~d} x \\ & \frac{v^{2}-v _{0}^{2}}{2}=a\left(x-x _{0}\right) \\ & v^{2}=v _{0}^{2}+2 a\left(x-x _{0}\right) \end{aligned} $$
इस विधि का लाभ यह है कि इसका प्रयोग असमान त्वरण वाले गति के लिए भी कर सकते हैं।
अब हम उपरोक्त समीकरणों का उपयोग कुछ महत्त्वपूर्ण उदाहरणों में करेंगे ।
उदाहरण 2.3 किसी बहुमंजिले भवन की ऊपरी छत से कोई गेंद $20 \mathrm{~m} \mathrm{~s}^{-1}$ के वेग से ऊपर की ओर ऊर्ध्वाधर दिशा में फेंकी गई है । जिस बिंदु से गेंद फेंकी गई है धरती से उसकी ऊँचाई $25.0 \mathrm{~m}$ है । (a) गेंद कितनी ऊपर जाएगी ?, तथा (b) गेंद धरती से टकराने के पहले कितना समय लेगी? $g=10 \mathrm{~m} \mathrm{~s}^{-2}$ ।
हल (a) $\mathrm{y}$-अक्ष को चित्र 2.6 में दिखाए गए अनुसार ऊर्ध्वाधर दिशा में ऊपर की ओर इस प्रकार चुनते हैं कि अक्ष का शून्य बिंदु धरती पर हो ।
$$ \begin{aligned} \text { अब, } \quad V _{o} & =+20 \mathrm{~m} \mathrm{~s}^{-1}, \\ a & =-g=-10 \mathrm{~m} \mathrm{~s}^{-2}, \\ V & =0 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
यदि फेंके गए बिंदु से गेंद $y$ ऊँचाई तक जाती है तो समीकरण $v^{2}=v _{0}^{2}+2 a\left(y-y _{0}\right)$ से हमें निम्नलिखित परिणाम मिलेगा $0=(20)^{2}+2(-10)\left(y-y _{0}\right)$, हल करने पर,
$\therefore y-y _{0}=20 \mathrm{~m}$
(b) इस खण्ड का उत्तर हम दो प्रकार से प्राप्त कर सकते हैं ।
इन दोनों विधियों को ध्यानपूर्वक समझें ।

चित्र 2.6
पहली विधि : इसमें, हम गेंद के मार्ग को दो भागों में विभाजित करते हैं : ऊपर की ओर गति ( $\mathrm{A}$ से $\mathrm{B}$ ) तथा नीचे की ओर गति $(\mathrm{B}$ से $\mathrm{C})$ तथा संगत समय $t _{1}$ व $t _{2}$ निकाल लेते हैं। क्योंकि $\mathrm{B}$ पर वेग शून्य है, इसलिए :
$$ \begin{aligned} & v=v_{\mathrm{o}}+a t \\ 0 & =20-10 t_1 \\ \text { या, } \quad \quad & t_1=2 \mathrm{~s} \end{aligned} $$
इस समय में गेंद बिंदु $\mathrm{A}$ से $\mathrm{B}$ पर पहुंचती है । $\mathrm{B}$ अर्थात अधिकतम ऊँचाई से गेंद गुरुत्वजनित त्वरण से मुक्त रूप से नीचे की ओर गिरती है । क्योंकि गेंद $y$ की ॠणात्मक दिशा के अनुदिश चलती है, इसलिए निम्नलिखित समीकरण का उपयोग करके हम $t _{2}$ का मान निकाल लेते हैं- $$ y=y _{0}+v _{0} t+\frac{1}{2} a t^{2} \quad \quad \quad \quad$$
हमें $y _{0}=45 \mathrm{~m}$ दिया है तथा $y=0, v _{0}=0, a=-g=$ $-10 \mathrm{~m} \mathrm{~s}^{-2}$
$\therefore 0=45+(1 / 2)(-10) t _{2}^{2}$ अतः $t _{2}=3 \mathrm{~s}$
इसलिए धरती पर टकराने के पहले गेंद द्वारा लिया गया कुल समय $t _{1}+t _{2}=2 \mathrm{~s}+3 \mathrm{~s}=5 \mathrm{~s}$ होगा ।
दूसरी विधि : मूल बिंदु के सापेक्ष गेंद के प्रारंभिक तथा अंतिम स्थितियों के निर्देशांकों को निम्नलिखित समीकरण में उपयोग करके हम गेंद द्वारा लिए गए कुल समय की गणना कर सकते हैं :
$$ \begin{aligned} & y=y _{0}+v _{0} t+\frac{1}{2} a t^{2} \\ & y=0 \mathrm{~m}, y _{0}=25 \mathrm{~m}, v _{0}=20 \mathrm{~m} \mathrm{~s}^{-1}, a=-10 \mathrm{~m} \mathrm{~s}^{-2}, \\ & t=? \\ & 0=25+20 t+(1 / 2)(-10) t^{2} \end{aligned} $$
या $5 t^{2}-20 t-25=0$
$t$ के लिए यदि इस द्विघाती समीकरण को हल करें, तो
$$ t=5 \mathrm{~s} $$
ध्यान दीजिए कि दूसरी विधि पहली से श्रेष्ठ है क्योंकि इसमें हमें गति के पथ की चिंता नहीं करनी है क्योंकि वस्तु स्थिर त्वरण से गतिमान है ।
उदाहरण 2.4 मुक्त पतन : स्वतंत्रतापूर्वक नीचे की ओर गिरती हुई वस्तु की गति का वर्णन कीजिए । वायुजनित प्रतिरोध की उपेक्षा की जा सकती है ।
हल यदि धरती की सतह से थोड़ी ऊंचाई पर से कोई वस्तु छोड़ दी जाए तो वह पृथ्वी की ओर गुरुत्व बल के कारण त्वरित होगी। गुरुत्वजनित त्वरण को हम $g$ से व्यक्त करते हैं। यदि वस्तु पर वायु के प्रतिरोध को हम नगण्य मानें तो हम कहेंगे कि वस्तु का पतन मुक्त रूप से हो रहा है। यदि गिरती हुई वस्तु द्वारा चली गई दूरी पृथ्वी की त्रिज्या की तुलना में बहुत कम है, तो हम $g$ के मान को स्थिर अर्थात $9.8 \mathrm{~m} \mathrm{~s}^{-2}$ ले सकते हैं। इस प्रकार मुक्त पतन एकसमान त्वरण वाली गति का एक उदाहरण है ।
हम यह मानेंगे कि वस्तु की गति $-y$ दिशा में है, क्योंकि ऊपर की दिशा को हम धनात्मक मानते हैं । गुरुत्वीय त्वरण की दिशा सदैव नीचे की ओर होती है, इसलिए इसे हम ऋणात्मक दिशा में लेते हैं ।
अतएव, $\quad a=-g=-9.8 \mathrm{~m} \mathrm{~s}^{-2}$
वस्तु को $y=0$ स्थिति में विरामावस्था से गिराते हैं । इसलिए $V _{0}=0$ और वस्तु के लिए गति संबंधी (2.9a) में दिए गए समीकरण निम्नलिखित प्रकार से व्यक्त किए जा सकते हैं-
$$ \begin{aligned} & V=0-g t=-9.8 t \mathrm{~m} \mathrm{~s}^{-1} \\ & y=0-1 / 2 g t^{2}=-4.9 t^{2} \mathrm{~m} \\ & v^{2}=0-2 g y=-19.6 y \mathrm{~m}^{2} \mathrm{~s}^{-2} \end{aligned} $$
ये समीकरण वस्तु के वेग, और उसके द्वारा चली गई दूरी को समय के फलन के रूप में तथा दूरी के सापेक्ष उसके वेग में परिवर्तन को व्यक्त करते हैं। समय के सापेक्ष त्वरण, वेग तथा दूरी के परिवर्तन को चित्र 2.7(a), (b) तथा (c) में दिखलाया गया है ।

(a)

(b)

(c)
चित्र 2.7 मुक्त पतन में वस्तु की गति ।
(a) समय के अनुरूप वस्तु के त्वरण में परिवर्तन,
(b) समय के अनुरूप वस्तु के वेग में परिवर्तन,
(c) समय के अनुरूप वस्तु की स्थिति में परिवर्तन।
उदाहरण 2.5 गैलीलियो का विषम अंक संबंधित नियम : इस नियम के अनुसार “विरामावस्था से गिरती हुई किसी वस्तु द्वारा समान समय अंतरालों में चली गई दूरियाँ एक दूसरे से उसी अनुपात में होती हैं जिस अनुपात में एक से प्रारंभ होने वाले विषम अंक [अर्थात $1: 3: 5$ : $7, \ldots \ldots .$. ]"। इस कथन को सिद्ध कीजिए ।
हल हम विरामावस्था से गिरती हुई किसी वस्तु के समय अंतराल को बहुत-से समान समय अंतरालों $\tau$ में विभक्त कर लेते हैं तथा क्रमशः इन समय अंतरालों में वस्तु द्वारा चली गई दूरी निकालते जाते हैं । इस स्थिति में वस्तु का प्रारंभिक वेग शून्य है, अत:
$$ y=-\frac{1}{2} g t^{2} $$
इस समीकरण की सहायता से हम भिन्न-भिन्न समय अंतरालों $0, \tau, 2 \tau, 3 \tau, \ldots \ldots$ में वस्तु की स्थितियों की गणना कर सकते हैं जिन्हें सारणी 2.2 के दूसरे कॉलम में दिखाया है । यदि प्रथम समय अंतराल $\tau$ पर वस्तु का स्थिति निर्देशांक $y _{0}$ लें $\left(y _{0}\right.$ $\left.=(-1 / 2) g \tau^{2}\right)$ तो आगे के समय अंतरालों के बाद वस्तु की स्थितियों को $y _{0}$ के मात्रक में कॉलम तीन में दिए गए तरीके से व्यक्त कर सकते हैं। क्रमिक समय अंतरालों (प्रत्येक $\tau$ ) में चली गई दूरियों को कॉलम चार में व्यक्त किया गया है । स्पष्ट है कि क्रमशः समय अंतरालों में वस्तु द्वारा चली गई दूरियाँ 1:3:5:7:9:11…. के सरल अनुपात में हैं जैसा कि अंतिम कॉलम में दिखाया गया है । इस नियम को सर्वप्रथम गैलीलियो गैलिली ( 1564-1642) ने प्रतिपादित किया था जिन्होंने मुक्त रूप से गिरती हुई वस्तु का पहली बार विधिवत परिमाणात्मक अध्ययन किया था ।
उदाहरण 2.6 वाहनों की अवरोधन दूरी : अवरोधन दूरी से हमारा अभिप्राय उस दूरी से है जो गतिमान वस्तु ब्रेक लगाने के कारण रुकने से पहले चल चुकी होती है । सड़क पर गतिमान वाहनों की सुरक्षा के संबंध में यह एक महत्त्वपूर्ण कारक है । यह दूरी वाहन के प्रारंभिक वेग $\left(V _{o}\right)$ तथा उसके ब्रेक की क्षमता या ब्रेक लगाए जाने के परिणामस्वरूप वाहन में उत्पन्न मंदन $-a$ पर निर्भर करती है। किसी वाहन की अवरोधन दूरी के लिए $v _{o}$ तथा $a$ के पदों में व्यंजक निकालिए।
सारिणी 2.2
| $t$ | $\boldsymbol{y}$ | $\boldsymbol{y}$ का मान, $\boldsymbol{y} _{0}$ के पदों में $\boldsymbol{y} _{o}\left[=(-1 / 2) \mathrm{g} \tau^{2}\right]$ |
क्रमिक समय अंतरालों में चली गई दूरी |
चली गई दूरियों का अनुपात |
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| $\tau$ | $-(1 / 2) \mathrm{g} \tau^{2}$ | $y _{o}$ | $y _{o}$ | 1 |
| $2 \tau$ | $-4(1 / 2) \mathrm{g} \tau^{2}$ | $4 y _{o}$ | $3 y _{o}$ | 3 |
| $3 \tau$ | $-9(1 / 2) \mathrm{g} \tau^{2}$ | $9 y _{o}$ | $5 y _{o}$ | 5 |
| $4 \tau$ | $-16(1 / 2) \mathrm{g} \tau^{2}$ | $16 y _{o}$ | $7 y _{o}$ | 7 |
| $5 \tau$ | $-25(1 / 2) \mathrm{g} \tau^{2}$ | $25 y _{o}$ | $9 y _{o}$ | 9 |
| $6 \tau$ | $-36(1 / 2) \mathrm{g} \tau^{2}$ | $36 y _{o}$ | $11 y _{o}$ | 11 |
हल मान लीजिए कि वाहन रुकने के पूर्व $d _{s}$ दूरी चल चुका है । गति संबंधी समीकरण $v^{2}=v _{0}^{2}+2 a x$ में यदि अंतिम वेग $V=0$ तो अवरोधन दूरी होगी।
$$ d _{s}=\frac{-v _{0}^{2}}{2 a} $$
अतः अवरोधन दूरी वाहन के प्रारंभिक वेग के वर्ग के समानुपाती होती है । यदि प्रारंभिक वेग को दूना कर दिया जाए तो उसी मंदन के लिए अवरोधन दूरी चार गुनी हो जाएगी। कार के किसी विशिष्ट मॉडल के लिए विभिन्न वेगों 11 , 15, 20 तथा $25 \mathrm{~m} \mathrm{~s}^{-1}$ के संगत अवरोधन दूरियाँ क्रमशः $10 \mathrm{~m}, 20 \mathrm{~m}, 34 \mathrm{~m}$ तथा $50 \mathrm{~m}$ पाई गई हैं जो उपरोक्त समीकरण से प्राप्त मानों के लगभग संगत हैं ।
कुछ क्षेत्रों, जैसे किसी विद्यालय के निकट वाहनों की चाल की सीमा के निर्धारण में अवरोधन दूरी का ज्ञान एक महत्त्वपूर्ण कारक होता है ।
उदाहरण 2.7 प्रतिक्रिया काल : कभी-कभी हमारे सामने ऐसी परिस्थिति पैदा हो जाती है कि हमसे तत्क्षण कार्यवाही की अपेक्षा की जाती है किंतु अनुक्रिया व्यक्त करने में हमसे कुछ समय लग जाता है । प्रतिक्रिया काल किसी व्यक्ति को कोई घटनाक्रम देखने में, उसके विषय में सोचने में तथा कार्यवाही करने में लगने वाला समय है । उदाहरणस्वरूप, मान लीजिए कि कोई व्यक्ति सड़क पर कार चला रहा है और अचानक रास्ते में एक लड़का सामने आ जाता है तो कार में तेजी से ब्रेक लगाने के पहले व्यक्ति को जो समय लग जाता है, उसे प्रतिक्रिया काल कहेंगे । प्रतिक्रिया काल परिस्थिति की जटिलता एवं व्यक्ति विशेष पर निर्भर करता है । आप स्वयं का प्रतिक्रिया काल एक साधारण प्रयोग द्वारा माप सकते हैं । आप अपने मित्र को एक रूलर दें और उससे कहें कि वह आपके हाथ के अंगूठे और तर्जनी के बीच की खाली जगह से रूलर ऊर्ध्राधर दिशा में गिरा दे (चित्र 2.8) । ज्योंही रूलर को छोड़ा जाए आप उसे पकड़ लें । इन दोनों घटनाओं (रूलर को छोड़ने तथा आपके द्वारा पकड़ने) के बीच लगे समय $t _{r}$ तथा रूलर द्वारा चली गई दूरी $d$ को नाप लें। किसी विशेष उदाहरण में $d=21.0$ $\mathrm{cm}$ है तो प्रतिक्रिया काल की गणना कीजिए।
चित्र 2.8 प्रतिक्रिया काल का मापन ।
हल रूलर मुक्त रूप से गिरता है, अत: $v _{0}=0, a=-g=-9.8$ $\mathrm{ms}^{-2}$ प्रतिक्रिया काल $t _{r}$ तथा तय की गई दूरी $(d)$ में संबंध है,
$$ \begin{aligned} d & =-\frac{1}{2} g t _{r}^{2} \\ \end{aligned} $$
$$ \begin{aligned} t _{r} & =\sqrt{\frac{2 d}{g}} \mathrm{~s} \end{aligned} $$
यदि $d=21.0 \mathrm{~cm}$ और $g=9.8 \mathrm{~ms}^{-2}$ है, तो
$$ t _{r}=\sqrt{\frac{2 \times 0.21}{9.8}} \mathrm{~s} \cong 0.2 \mathrm{~s} $$
सारांश
1. यदि किसी वस्तु की स्थिति समय के साथ बदलती है तो हम कहते हैं कि वस्तु गतिमान है। एक सरल रैखिक गति में वस्तु की स्थिति को सुगमता के दृष्टिकोण से चुने गए किसी मूल बिंदु के सापेक्ष निर्दिष्ट किया जा सकता है । मूल बिंदु के दायों ओर की स्थितियों को धनात्मक तथा बायों ओर की स्थितियों को ऋणात्मक कहा जाता है । किसी वस्तु द्वारा चली गई दूरी की लंबाई को पथ-लंबाई के रूप में परिभाषित करते हैं ।
2. जब समय अतंराल $\Delta t$ अत्यल्प हो तो वस्तु के औसत वेग के सीमान्त मान को तात्क्षणिक वेग या केवल वेग कहते हैं :
$$ v=\lim _{\Delta t \rightarrow 0} \bar{v}=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{\mathrm{d} x}{\mathrm{~d} t} $$
किसी क्षण वस्तु का वेग उस क्षण स्थान समय-ग्राफ की प्रवणता के बराबर होता है ।
3. वस्तु के वेग में परिवर्तन को संगत समय अंतराल से विभाजित करने पर जो राशि प्राप्त होती है, उसे औसत त्वरण कहते हैं :
$$ \bar{a}=\frac{\Delta v}{\Delta t} $$
4. जब समय अंतराल अत्यल्प $\Delta t \rightarrow 0$ हो तो, वस्तु के औसत त्वरण के सीमान्त मान को तात्क्षणिक त्वरण या केवल त्वरण कहते हैं :
$$ a=\lim _{\Delta t \rightarrow 0} \bar{a}=\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{\mathrm{d} v}{\mathrm{~d} t} $$
किसी क्षण वस्तु का त्वरण उस क्षण वेग-समय ग्राफ की प्रवणता के बराबर होता है । एकसमान गति के लिए त्वरण शून्य होता है तथा $X-t$ ग्राफ समय-अक्ष पर आनत एक सरल रेखा होती है । इसी प्रकार एकसमान गति के लिए $v-t$ ग्राफ समय-अक्ष के समांतर सरल रेखा होती है । एकसमान त्वरण के लिए $x-t$ ग्राफ परवलय होता है जबकि $V-t$ ग्राफ समय-अक्ष के आनत एक सरल रेखा होती है ।
5. किन्हीं दो क्षणों $t _{1}$ तथा $t _{2}$ के मध्य खींचे गए वेग-समय वक्र के अंतर्गत आने वाला क्षेत्रफल वस्तु के विस्थापन के बराबर होता है ।
6. एकसमान त्वरण से गतिमान वस्तु के लिए कुछ सामान्य समीकरणों का एक समूह होता है जिससे पाँच राशियाँ यथा विस्थापन $X$, तत्संबंधित समय $t$, प्रारंभिक वेग $v _{\mathrm{o}}$, अंतिम वेग $v$ तथा त्वरण $a$ एक दूसरे से संबंधित होते हैं । इन समीकरणों को वस्तु के शुद्धगतिक समीकरणों के नाम से जाना जाता है :
$$ \begin{aligned} & v=v _{o}+a t & x=v _{0} t+\frac{1}{2} a t^{2} \\ & v^{2}=v _{0}^{2}+2 a x \end{aligned} $$
इन समीकरणों में क्षण $t=0$ पर वस्तु की स्थिति $x=0$ ली गई है । यदि वस्तु $x=x _{o}$ से चलना प्रारंभ करे तो उपर्युक्त समीकरणों में $x$ के स्थान पर $\left(x-x _{0}\right)$ लिखेंगे ।
| भौतिक राशि | प्रतीक | विमाएँ | मात्रक | टिफ्फणी |
|---|---|---|---|---|
| पथ-लंबाई | [L] | $\mathrm{m}$ | ||
| विस्थपन | $\Delta x$ | [L] | $\mathrm{m}$ | $=x_2-x_1$ एक विमा में इसका चिह्ह दिशा को इंगित करता है । |
| वेग (a) औसत (b) तात्क्षणिक |
$\bar{v}$ $v$ |
$\left[\mathrm{LT}^{-1}\right]$ | $=\frac{\Delta x}{\Delta t}$ $=\lim _{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=\frac{\mathrm{d} x}{\mathrm{dt}}$ एक विमा में इसका चिह्ध दिशा को इंगत करता है |
|
| चाल (a) औसत (b) तात्क्षणिक |
$=\frac{\text { पथ-लंबाई }}{\text { समय अंतराल }}$ $=\frac{\mathrm{d} x}{\mathrm{dt}}$ |
|||
| त्वरण (a) औसत (b) तात्क्षणिक |
$a$ | $\left[\mathrm{LT}^{-2}\right.$ | $\mathrm{m} \mathrm{s}^{-2}$ | $=\frac{\Delta v}{\Delta t}$ $=\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}=\frac{\mathrm{d} v}{\mathrm{~d} t}$ एक विमा में इसका चिह्ध दिशा को इंगित करता है |
विचारणीय विषय
1. मूल बिंदु तथा किसी अक्ष की धनात्मक दिशा का चयन अपनी रुचि का विषय है । आपको सबसे पहले इस चयन का उल्लेख कर देना चाहिए और इसी के बाद राशियों; जैसे- विस्थापन, वेग तथा त्वरण के चिह्नों का निर्धारण करना चाहिए।
2. यदि किसी वस्तु की चाल बढ़ती जा रही है तो त्वरण वेग की दिशा में होगा परंतु यदि चाल घटती जाती है तो त्वरण वेग की विपरीत दिशा में होगा । यह कथन मूल बिंदु तथा अक्ष के चुनाव पर निर्भर नहीं करता ।
3. त्वरण के चिह्न से हमें यह पता नहीं चलता कि वस्तु की चाल बढ़ रही है या घट रही है । त्वरण का चि्न (जैसा कि उपरोक्त बिंदु 1 में बतलाया गया है) अक्ष के धनात्मक दिशा के चयन पर निर्भर करता है । उदाहरण के तौर पर यदि ऊपर की ओर ऊर्ध्वाधर दिशा को अक्ष की धनात्मक दिशा माना जाए तो गुरुत्वजनित त्वरण ऋणात्मक होगा। यदि कोई वस्तु गुरुत्व के कारण नीचे की ओर गिर रही है तो भी वस्तु की चाल बढ़ती जाएगी यद्यपि त्वरण का मान ऋणात्मक है। वस्तु ऊपर की दिशा में फेंकी जाए तो उसी ॠणात्मक (गुरुत्वजनित) त्वरण के कारण वस्तु की चाल में कमी आती जाएगी।
4. यदि किसी क्षण वस्तु का वेग शून्य है तो यह आवश्यक नहीं है कि उस क्षण उसका त्वरण भी शून्य हो । कोई वस्तु क्षणिक रूप से विरामावस्था में हो सकती है तथापि उस क्षण उसका त्वरण शून्य नहीं होगा । उदाहरणस्वरूप, यदि किसी वस्तु को ऊपर की ओर फेंका जाए तो शीर्षस्थ बिंदु पर उसका वेग तो शून्य होगा परंतु इस अवसर पर उसका त्वरण गुरुत्वजनित त्वरण ही होगा ।
5. गति संबंधी शुद्धगतिक समीकरणों [समीकरण (2.9)] की विभिन्न राशियाँ बीजगणितीय हैं अर्थात वे धनात्मक या ऋणात्मक हो सकती हैं। ये समीकरण सभी परिस्थितियों (स्थिर त्वरण वाली एकविमीय गति) के लिए उपयुक्त होते हैं बशर्ते समीकरणों में विभिन्न राशियों के मान उपयुक्त चिह्नों के साथ रखे जाएँ ।
6. तात्क्षणिक वेग तथा त्वरण की परिभाषाएँ [समीकरण (2.1) तथा समीकरण (2.3)] यथार्थ हैं और सदैव सही हैं जबकि शुद्धगतिक समीकरण [समीकरण (2.9)] उन्हीं गतियों के लिए सही है जिनमें गति की अवधि में त्वरण का परिमाण और दिशा स्थिर रहते हैं ।
अभ्यास
2.1 नीचे दिए गए गति के कौन से उदाहरणों में वस्तु को लगभग बिंदु वस्तु माना जा सकता है :
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकिल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बंदर ।
(c) जमीन से टकरा कर तेजी से मुड़ने वाली क्रिकेट की कोई फिरकती गेंद ।
(d) किसी मेज के किनारे से फिसल कर गिरा कोई बीकर ।
Show Answer
#content missing2.2 दो बच्चे $\mathrm{A}$ व $\mathrm{B}$ अपने विद्यालय $\mathrm{O}$ से लौट कर अपने-अपने घर क्रमशः $\mathrm{P}$ तथा $\mathrm{Q}$ को जा रहे हैं । उनके स्थिति-समय $(x-t)$ ग्राफ चित्र 2.9 में दिखाए गए हैं । नीचे लिखे कोष्ठकों में सही प्रविष्टियों को चुनिए :
(a) $\mathrm{B} / \mathrm{A}$ की तुलना में $\mathrm{A} / \mathrm{B}$ विद्यालय से निकट रहता है ।
(b) $\mathrm{B} / \mathrm{A}$ की तुलना में $\mathrm{A} / \mathrm{B}$ विद्यालय से पहले चलता है ।
(c) $\mathrm{B} / \mathrm{A}$ की तुलना $\mathrm{A} / \mathrm{B}$ तेज चलता है ।
(d) $\mathrm{A}$ और $\mathrm{B}$ घर (एक ही/भिन्न) समय पर पहुँचते हैं ।
(e) $\mathrm{A} / \mathrm{B}$ सड़क पर $\mathrm{B} / \mathrm{A}$ से (एक बार/दो बार) आगे हो जाते हैं ।
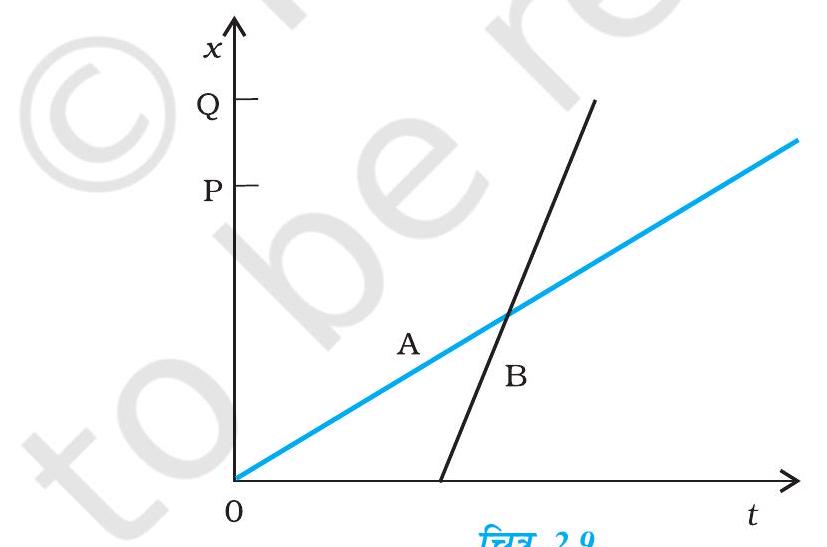
चित्र 2.9
Show Answer
#content missing2.3 एक महिला अपने घर से प्रातः 9.00 बजे $2.5 \mathrm{~km}$ दूर अपने कार्यालय के लिए सीधी सड़क पर $5 \mathrm{~km} \mathrm{~h}^{-1}$ चाल से चलती है । वहाँ वह सायं 5.00 बजे तक रहती है और $25 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से चल रही किसी ऑटो रिक्शा द्वारा अपने घर लौट आती है । उपयुक्त पैमाना चुनिए तथा उसकी गति का $x-t$ ग्राफ खींचिए ।
Show Answer
#content missing2.4 कोई शराबी किसी तंग गली में 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, उसके बाद फिर 5 कदम आगे बढ़ता है और 3 कदम पीछे आता है, और इसी तरह वह चलता रहता है । उसका हर कदम $1 \mathrm{~m}$ लंबा है और $1 \mathrm{~s}$ समय लगता है। उसकी गति का $x-t$ ग्राफ खींचिए । ग्राफ से तथा किसी अन्य विधि से यह ज्ञात कीजिए कि वह जहां से चलना प्रारंभ करता है वहाँ से $13 \mathrm{~m}$ दूर किसी गड्ढे में कितने समय पश्चात गिरता है ।
Show Answer
#content missing2.5 कोई जेट वायुयान $500 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से चल रहा है और यह जेट यान के सापेक्ष $1500 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से अपने दहन उत्पादों को बाहर निकालता है । जमीन पर खड़े किसी प्रेक्षक के सापेक्ष इन दहन उत्पादों की चाल क्या होगी ?
Show Answer
#content missing2.6 सीधे राजमार्ग पर कोई कार $126 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से चल रही है । इसे $200 \mathrm{~m}$ की दूरी पर रोक दिया जाता है । कार के मंदन को एकसमान मानिए और इसका मान निकालिए । कार को रुकने में कितना समय लगा ?
#content missing
#content missing
#content missing
#content missing
Show Answer
#content missing2.7 कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल $29 \mathrm{~m} \mathrm{~s}^{-1}$ से फेंकता है,
(i) गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी ?
(ii) इसकी गति के उच्चतम बिंदु पर गेंद के वेग व त्वरण क्या होंगे ?
(iii) गेंद के उच्चतम बिंदु पर स्थान व समय को $x=0$ व $t=0$ चुनिए, ऊर्ध्वाधर नीचे की ओर की दिशा को $x$ अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिह्न बताइए।
(iv) किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है ?
$$ \text { [ } g=9.8 \mathrm{~m} \mathrm{~s}^{-2} \text { तथा वायु का प्रतिरोध नगण्य है ।] } $$
Show Answer
#content missing2.8 नीचे दिए गए कथनों को ध्यान से पढ़िए और कारण बताते हुए व उदाहरण देते हुए बताइए कि वे सत्य हैं या असत्य, एकविमीय गति में किसी कण की
(a) किसी क्षण चाल शून्य होने पर भी उसका त्वरण अशून्य हो सकता है ।
(b) चाल शून्य होने पर भी उसका वेग अशून्य हो सकता है ।
(c) चाल स्थिर हो तो त्वरण अवश्य ही शून्य होना चाहिए ।
(d) चाल अवश्य ही बढ़ती रहेगी, यदि उसका त्वरण धनात्मक हो ।
Show Answer
#content missing2.9 किसी गेंद को $90 \mathrm{~m}$ की ऊँचाई से फर्श पर गिराया जाता है । फर्श के साथ प्रत्येक टक्कर में गेंद की चाल $1 / 10$ कम हो जाती है । इसकी गति का $t=0$ से $12 \mathrm{~s}$ के बीच चाल-समय ग्राफ खींचिए ।
#content missing
#content missing
Show Answer
#content missing2.10 उदाहरण सहित निम्नलिखित के बीच के अंतर को स्पष्ट कीजिए : (a) किसी समय अंतराल में विस्थापन के परिमाण (जिसे कभी-कभी दूरी भी कहा जाता है) और किसी कण द्वारा उसी अंतराल के दौरान तय किए गए पथ की कुल लंबाई ।
(b) किसी समय अंतराल में औसत वेग के परिमाण और उसी अंतराल में औसत चाल (किसी समय अंतराल में किसी कण की औसत चाल को समय अंतराल द्वारा विभाजित की गई कुल पथ-लंबाई के रूप में परिभाषित किया जाता है । प्रदर्शित कीजिए कि $(\mathrm{a})$ व $(\mathrm{b})$ दोनों में ही दूसरी राशि पहली से अधिक या उसके बराबर है । समता का चिह्न कब सत्य होता है ? (सरलता के लिए केवल एकविमीय गति पर विचार कीजिए ।)
#content missing
#content missing
#content missing
Show Answer
#content missing2.11 कोई व्यक्ति अपने घर से सीधी सड़क पर $5 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से $2.5 \mathrm{~km}$ दूर बाजार तक पैदल चलता है । परंतु बाजार बंद देखकर वह उसी क्षण वापस मुड़ जाता है तथा $7.5 \mathrm{~km} \mathrm{~h}^{-1}$ की चाल से घर लौट आता है ।समय अंतराल (i) 0 - 30 मिनट, (ii) 0 - 50 मिनट, (iii) 0 - 40 मिनट की अवधि में उस व्यक्ति (a) के माध्य वेग का परिमाण, तथा (b) का माध्य चाल क्या है? (नोट : आप इस उदाहरण से समझ सकेंगे कि औसत चाल को औसत-वेग के परिमाण के रूप में परिभाषित करने की अपेक्षा समय द्वारा विभाजित कुल पथ-लंबाई के रूप में परिभाषित करना अधिक अच्छा क्यों है । आप थक कर घर लौटे उस व्यक्ति को यह बताना नहीं चाहेंगे कि उसकी औसत चाल शून्य थी ।)
Show Answer
#content missing2.12 हमने अभ्यास 2.9 तथा 2.10 में औसत चाल व औसत वेग के परिमाण के बीच के अंतर को स्पष्ट किया है । यदि हम तात्क्षणिक चाल व वेग के परिमाण पर विचार करते हैं तो इस तरह का अंतर करना आवश्यक नहीं होता । तात्क्षणिक चाल हमेशा तात्क्षणिक वेग के बराबर होती है । क्यों ?
Show Answer
#content missing2.13 चित्र 2.10 में (a) से (d) तक के ग्राफों को ध्यान से देखिए और देखकर बताइए कि इनमें से कौन-सा ग्राफ एकविमीय गति को संभवत: नहीं दर्शा सकता ।
चित्र 2.10
Show Answer
#content missing2.14 चित्र 2.11 में किसी कण की एकविमीय गति का $x$ - $t$ ग्राफ दिखाया गया है । ग्राफ से क्या यह कहना ठीक होगा कि यह कण $t<0$ के लिए किसी सरल रेखा में और $t>0$ के लिए किसी परवलीय पथ में गति करता है । यदि नहीं, तो ग्राफ के संगत किसी उचित भौतिक संदर्भ का सुझाव दीजिए ।
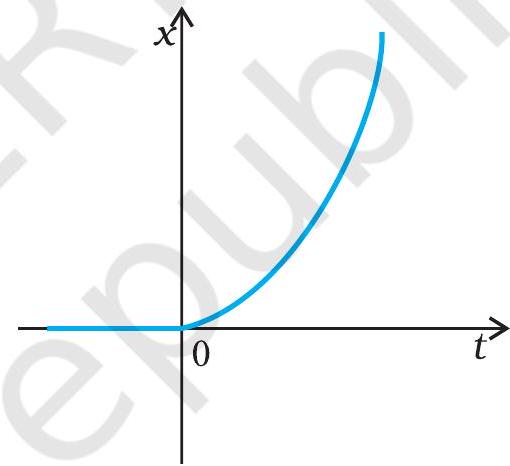
चित्र 2.11
Show Answer
#content missing2.15 चित्र 2.12 में दिखाए गए प्रत्येक ग्राफ के लिए किसी उचित भौतिक स्थिति का सुझाव दीजिए :

चित्र 2.12
Show Answer
#content missing2.16 चित्र 2.13 में किसी कण की एकविमीय सरल आवर्ती गति के लिए $x-t$ ग्राफ दिखाया गया है । (इस गति के बारे में आप अध्याय 13 में पढ़ेंगे) समय $t=0.3 \mathrm{~s}, 1.2 \mathrm{~s},-1.2 \mathrm{~s}$ पर कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे ?
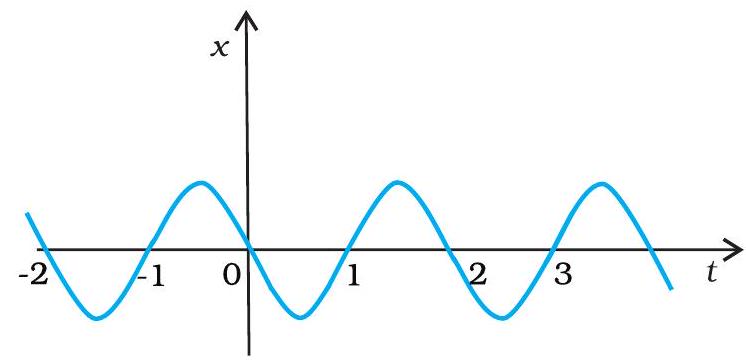
चित्र 2.13
Show Answer
#content missing2.17 चित्र 2.14 किसी कण की एकविमीय गति का $x-t$ ग्राफ दर्शाता है । इसमें तीन समान अंतराल दिखाए गए हैं। किस अंतराल में औसत चाल अधिकतम है और किसमें न्यूनतम है ? प्रत्येक अंतराल के लिए औसत वेग का चिह्न बताइए।
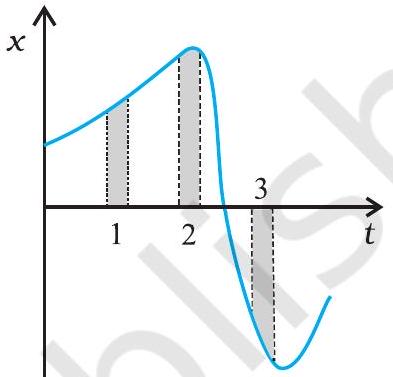
चित्र 2.14
Show Answer
#content missing2.18 चित्र 2.15 में किसी नियत (स्थिर) दिशा के अनुदिश चल रहे कण का चाल-समय ग्राफ दिखाया गया है। इसमें तीन समान समय अंतराल दिखाए गए हैं । किस अंतराल में औसत त्वरण का परिमाण अधिकतम होगा ? किस अंतराल में औसत चाल अधिकतम होगी ? धनात्मक दिशा को गति की स्थिर दिशा चुनते हुए तीनों अंतरालों में $v$ तथा $a$ के चिह्न बताइए। $\mathrm{A}, \mathrm{B}, \mathrm{C}$, व $\mathrm{D}$ बिंदुओं पर त्वरण क्या होंगे ?
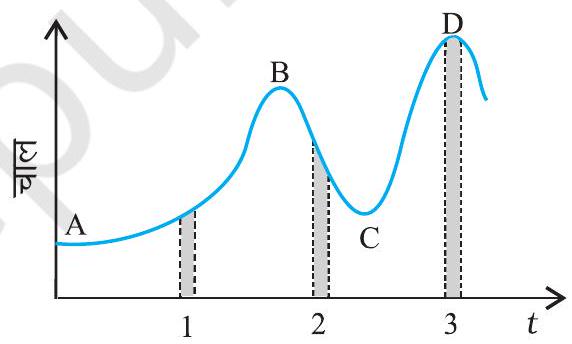
चित्र 2.15





