अध्याय 10

तरलों की यांत्रिकीय गुणधर्म

MCQ I

10.1 एक ऊँचा सिलेंडर विस्कोज तेल से भरा हुआ है। शून्य प्रारंभिक वेगशीलता के साथ एक गोल पत्थर ऊपर से डाला जाता है। चित्र 10.1 में दिखाई गई प्लॉट से, समय $(t)$ के आधार पर पत्थर $(v)$ की वेगशीलता को दिखाएँ।

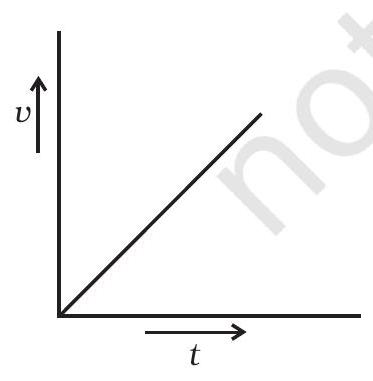
(a)

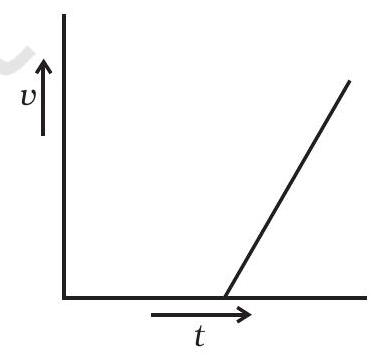
(b)

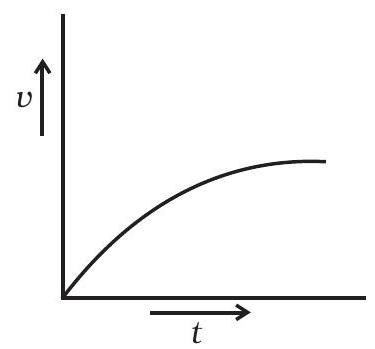
(c)

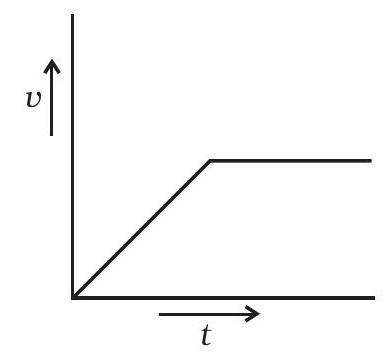
(d)

चित्र 10.1

10.2 निम्नलिखित में से कौन सा आरेख एक स्ट्रीमलाइन प्रवाह को नहीं दर्शाता है? (चित्र 10.2)

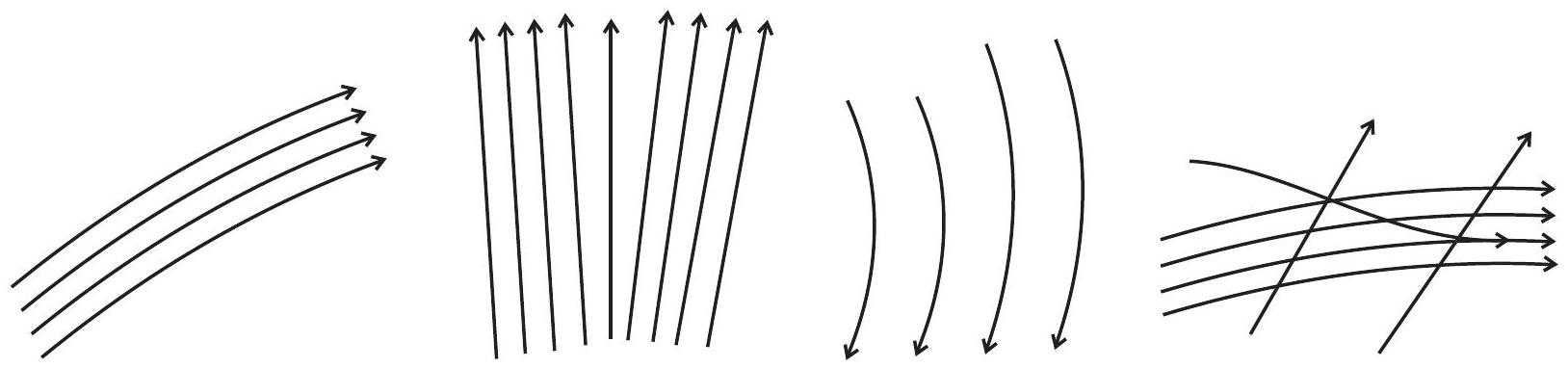
चित्र 10.2

10.3 एक स्ट्रीमलाइन पर

(a) तरल कण की वेगशीलता स्थिर रहती है।

(b) दिए गए स्थान पर पार करने वाले सभी तरल कणों की वेगशीलता स्थिर होती है।

(c) एक निश्चित क्षण में सभी तरल कणों की वेगशीलता स्थिर होती है।

(d) तरल कण की गति स्थिर रहती है।

10.4 एक आदर्श तरल दो भागों में बनी हुई वृत्ताकार क्रॉस-सेक्शन वाले पाइप से बहता है, उन दोनों सेक्शनों का व्यास $2.5 \mathrm{~सेमी}$ और $3.75 \mathrm{~सेमी}$ है। दोनों पाइप में वेगों का अनुपात है

(a) $9: 4$

(b) $3: 2$

(c) $√3: √2$

(d) $√2: √3$

10.5 जल-कांच की सतह पर संपर्क का कोण $0^{\circ}$ है, एथिल एल्कोहल-कांच पर संपर्क का कोण $0^{\circ}$ है, मर्क्यूरी-कांच पर संपर्क का कोण $140^{\circ}$ है और मेथिलआयोडाइड-कांच पर संपर्क का कोण $30^{\circ}$ है। एक कांच का कैपिलरी उस छलनी में रखा गया है जिसमें से चारों द्रवयों में से एक है। यह देखा जाता है कि मेनिस्कस उत्तल है। छलनी में द्रव है

(a) जल

(b) एथिल एल्कोहल

(c) मर्क्यूरी

(d) मेथिलायोडाइड।

MCQ II

10.6 किसी सतह के अणु के लिए

(a) इसे शून्य बल प्रभावित नहीं करता है।

(b) उस पर एक नेट नीचे की असर होती है।

(c) संभावनात्मक ऊर्जा उसके भीतर के अणु की ऊर्जा से कम होती है।

(d) संभावनात्मक ऊर्जा उसके भीतर के अणु की ऊर्जा से अधिक होती है।

10.7 दबाव एक स्केलर मात्रा है क्योंकि

(a) यह बल के प्रतिशत से क्षेत्र का अनुपात होता है और दोनों बल और क्षेत्र वेक्टर होते हैं।

(b) यह शक्ति की अद्यतन क्षेत्रीयता के मान के अनुपात है।

(c) यह बल के क्षेत्र के नियमानुरूप संघातांक है।

(d) यह क्षेत्र के चयनित आकार पर निर्भर नहीं करता है।

10.8 एक लकड़ी का ब्लॉक जिस पर एक सिक्का रखा हुआ है, पानी में तैरता है जैसा कि चित्र में दिखाया गया है। चित्र 10.3 में दिखाए गए हैं।

तत्परता $l$ और $h$ चित्र में दिखाए गए हैं। कुछ समय बाद सिक्का पानी में गिर जाता है। तभी

(a) $l$ कम हो जाता है।

(b) $h$ कम हो जाता है।

कॉ प्रशंसापत्र प्रकार: (सी) $ल$ बढ़ता है।

(डी) $h$ बढ़ता है।

चित्र 10.3

** 10.9 ** तापमान में वास्तविकता बढ़ते ही,

(ए) वायु का द्रवीयता कम होती है।

(बी) तरल पदार्थों की वास्तविकता बढ़ती है।

(सी) वायु का द्रवीयता बढ़ती है।

(डी) तरल पदार्थों की वास्तविकता कम होती है।

** 10.10 ** स्ट्रीमलाइन प्रवाह बारीकी के साथ होता है

(ए) ऊंचा घनत्व।

(बी) ऊंची द्रवीयता।

(सी) कम घनत्व।

(डी) कम द्रवीयता।

वनिता श्रेणी

** 10.11 ** क्या द्रवीयता एक वेक्टर है?

** 10.12 ** क्या सतह तनाव एक वेक्टर है?

** 10.13 ** हिमपात जल में तैरता है जिसका हिस्सा डूबता है। हिम का घनत्व $\rho_{i}=$ $0.917 \mathrm{~ग्राम}\mathrm{~सेमी}^{-3}$ है।

** 10.14 ** पानी से भरी हुई एक वास्तुय विएसल को एक वजनी पैन पर रखा जाता है और ताली को शून्य पर सेट किया जाता है। एक कदमहीन हल्के द्वारा लटका हुआ एक गति के विझूम अस्प्रिंग के द्वारा इस ब्लॉक को पानी में डूबा दिया है। स्केल की पढ़ाई क्या है?

** 10.15 ** एक घनत्व वाले एक घनत्व वाले एक घनत्व के गहराई $L$ की सतह पर तैरते हैं। पत्रिका एक ऋणवाही तेजी के साथ गति हो रही है जो है। कितने डूबा हुआ है?

संख्या

** 10.16 ** पेड़ों में रस, जो गर्म मौसम में मुख्य रूप से पानी से मिलकर बनता है, का एक प्रणाली में उनी बढ़ता हुआ है,तट्टु रायीट। रस का तनाव मान $T=7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ है और संपर्क का कोण है $0^{\circ}$ है। क्या सतह तनाव सिर्फ वृक्षों की शीर्ष पर पानी की आपूर्ति के लिए लाभदायक है?

** 10.17 ** टेंकर में तेल की मुक्त सतह, शांत होते होते, क्षैतिज है। यदि टेंकर तेजी से गतिशील होती है, तो मुक्त सतह को एक कोण $\theta$ द्वारा टिल किया जाएगा। यदि त्वरण $a \mathrm{~मी} \mathrm{~सेकंड}^{-2}$ है, तो मुक्त सतह का स्रोत क्या होगा?

** 10.18 ** $0.1 \mathrm{~सेमी}$ और $0.2 \mathrm{~सेमी}$ त्रिवृत्तियों का संकुचित हो जाना। जारी रख दिया। मरक्का मान $T=435.5 \times 10^{-3} \mathrm{~एन} \mathrm{~मी}^{-1}$।

** 10.19 ** यदि संकुचितता की बूंद छोटे छोटे बूंदों में तोड़ दी जाती है, तो बूंदों का तापमान कम हो जाता है। एक ठंडे के तापमान में ड्रॉप का ओर रेडियस करें $R$, तोड़ दें $N$ में हर एक के तापमान का अनुमान लगाएं।

** 10.20 ** पानी की सतही तनाव और वाष्पशक्ति $20^{\circ} \mathrm{C}$ में $7.28 \times 10^{-2} \mathrm{Nm}^{-1}$ और $2.33 \times 10^{3} \mathrm{~पास्कल}$ है। $20^{\circ} \mathrm{C}$ पर वाष्पित होने के बिना बन सकने वाली सबसे छोटी गोलाकार पानी की तितली क्या है?

वितर्कता पुस्तिका

** 10.21 ** (क) एक व्यक्ति वायुमंडल में उत्पन्न होते वायु का घनत्व है $\rho$, तो घनत्व $\rho_{0}$ से क्या है और विभाजन की मात्रा की बदलती है $\mathrm{d} p$ प्रतिस्थानि $\mathrm{d} h$?

(बी) दबाव $p$ को घनत्व के अनुपात मानते हुए, पृष्ठ पर दबाव $p$ क्या होगा अगर पृथ्वी की सतह पर दबाव $p_{0}$ है?

(c) यदि $p_{0}=1.03 \times 10^{5} \mathrm{~N} \mathrm{~m}^{-2}, \rho_{0}=1.29 \mathrm{~kg} \mathrm{~m}^{-3}$, और $g=9.8 \mathrm{~m} \mathrm{~s}^{-2}$ है, तो भूमि की सतह पर तापमान के पाठ की मान की $(1 / 10)$ का छहाने वाली चीज का किस स्तर पर होगा?

(d) हवा पर का यह मॉडल छोटी दूरियों के लिए कार्य करता है। मॉडल की सीमा क्या है जो मॉडल को सीमित करती है?

10.22 पारदर्शिता द्वारा प्रदर्शित होती है, पानी के अणुओं के बीच के आकर्षण के कारण। पारदर्शिता तापमान में वृद्धि के साथ कम होती है और उबलने के बिंदु पर मिट जाती है। यदि पानी के वाष्पीकरण तापल के लिए $L_{v}=540 \mathrm{k} \mathrm{cal} \mathrm{kg}^{-1}$, वेगवती के यंत्रिकीय समरूप, जतस्थानीय कतनी $\mathrm{J}=4.2 \mathrm{~J} \mathrm{cal}^{-1}$, पानी का घनत्व $\rho_{\mathrm{w}}=10^{3} \mathrm{~kg} t^{-1}$, अवगाड्रो का संख्या $N_{\mathrm{A}}=6.0 \times 10^{26} \mathrm{k} \mathrm{mole}^{-1}$ और पानी का आणविक भार $M_{\mathrm{A}}=18 \mathrm{~kg}$ है $1 \mathrm{kmole}$ के लिए।

(a) पानी के एक अणु के वाष्पीभवन के लिए ऊर्जा का आकलन करें।

(b) दिखाएँ कि पानी के अणुओं के बीच का अंतःसन्निकटता $d=\left[\frac{M_{\mathrm{A}}}{N_{\mathrm{A}}} \times \frac{1}{\rho_{w}}\right]^{1 / 3}$ है और इसका मान निकालें।

(c) $1 \mathrm{~ग्राम}$ वाष्पित रूप में पानी $1 \mathrm{~एटमॉस्फियर}$ में $1601 \mathrm{~सेंटीमीटर}^{3}$ क्षेत्रफल का कठिनाई का अंतःसन्निकटता लगाएं।

(d) वाष्पिकरण के दौरान एक अणु $F$ को पार करता है, स्नातक के बीच अंतःसन्निकटता $d$ से $d^{\prime}$ तक। $F$ के मान का आकलन करें।

(e) सतह तनाव का माप है, $F / d$ की गणना करें।

10.23 एक गर्म हवा गुब्बारा एक गोला है जिसका त्रिज्या $8 \mathrm{~मीटर}$ है। गुब्बारे के अंदर का हवा एक तापमान पर है $60^{\circ} \mathrm{C}$। जब बाहरी तापमान $20^{\circ} \mathrm{C}$ हो तो गुब्बारा कितना भार उठा सकता है? (हवा को एक आदर्श गैस माना जाए, $R=8.314 \mathrm{~J} \mathrm{~मोल}^{-1} \mathrm{~K}^{-1}, 1 \mathrm{~एटमॉस्फियर} .=1.013 \times 10^{5} \mathrm{~पास्काल}$; परिपत्र का तनाव $5 \mathrm{~न्यूटन} \mathrm{~मीटर}^{-1}$ है।)

वस्त्रीकृती का ही संस्करण $m_{जहाज}+m_{पानी}+\rho_{जल} V g$ है।

चूंकि ब्लॉक के बिना स्केल को शून्य पर समायोजित किया गया है, इसलिए नया पठन यह है $\rho_{जल} V g$।

10.15 जल का घनत्व $\rho_{w}$ होने दें।

तब $\rho a L^{3}+\rho L^{3} g=\rho_{जल} x L^{3}(g+a)$ होगा।

$\therefore x=\frac{\rho}{\rho_{जल}}$ होगा।

इस प्रकार, खंड डुबने का अंश किसी भी त्वरण के अलावा, चाहे वज्रागणि या लिफ्ट भूगोल, पर निर्भर नहीं होता है।

10.16 जैसी ऊंचाई जिस पर Ras उठेगा वह होगी:

$h=\frac{2 T \cos 0^{\circ}}{\rho g r}=\frac{2\left(7.2 \times 10^{-2}\right)}{10^{3} \times 9.8 \times 2.5 \times 10^{-5}} \quad 0.6 \mathrm{~m}$

यह सतह पर ऊठने की अधिकतम ऊंचाई है। क्योंकि कई पेड़ों की ऊंचाई इससे ज्यादा होती है, इसलिए केपिलरी गतिविधि ही सभी पेड़ों में पानी के उठान का कारण नहीं हो सकती है।

10.17 यदि टैंकर सक्षमान बाधता को ले तांडविषण के सक्षमान में बदलता है, तो पानी टैंकर के पीछे तनावित होगा। स्वतंत्र सतह ऐसी होगी कि किसी भी द्रव भाग के लिए केंद्रिय बल शून्य होता है।

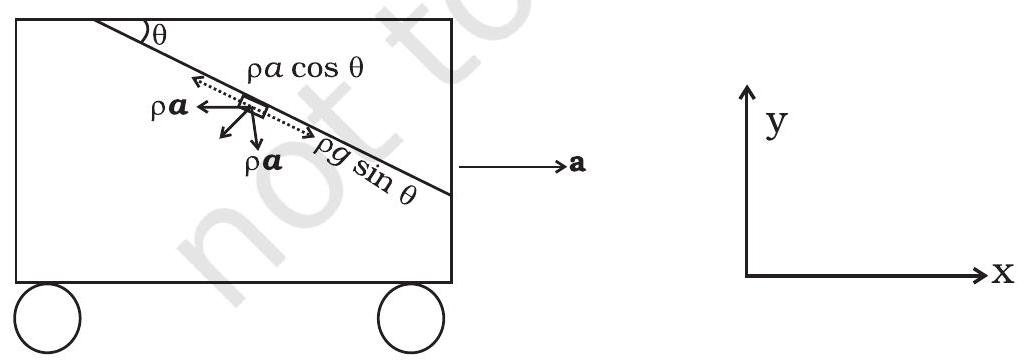
उपकरण पर विचार करें, घुटने पर एक द्रव्यमय मोड़ की, इकाई आयतन के। द्रव्य पर कार्यों की और

$-\rho g \hat{\mathbf{y}}$ और $\quad-\rho a \hat{\mathbf{x}}$ हैं।

सतह के सापेक्षिक वजन की तत्त्विक हिस्सा है $\rho g \sin \theta$

तत्त्वीय के उससे उत्पन्न बाधा सापेक्षिक हिस्सा है

$\rho a \cos \theta$

$\therefore \rho g \sin \theta=\rho a \cos \theta$

इसलिए, $\tan \theta=a / g$

10.18 $v_{1}$ और $v_{2}$ बूंदों का आयाम और $v$ परिणामी बूंद का है।

तब $v=v_{1}+v_{2}$

$\Rightarrow r^{3}=r_{1}^{3}+r_{2}^{3}=(0.001+0.008) \mathrm{cm}^{3}=0.009 \mathrm{~cm}^{3}$

$\therefore r \quad 0.21 \mathrm{~cm}$

$\therefore \Delta U=4 \pi T\left(r^{2}-\left(r_{1}^{2}+r_{2}^{2}\right)\right)$

$=4 \pi \times 435.5 \times 10^{-3}\left(0.21^{2}-0.05\right) \times 10^{-4} \mathrm{~J}$

$$ -32 \times 10^{-7} \mathrm{~J} $$

10.19 $R^{3}=N r^{3}$

$\Rightarrow r=\frac{R}{N^{1 / 3}}$ होगा।

$\Delta U=4 \pi T\left(R^{2}-N r^{2}\right)$

यदि सभी ऊर्जा को संक्षेप में छोड़ा जाता है तो यह ऊष्णता को कम करने के भुगतान के रूप में होगा। यदि $s$ विशिष्ट ऊष्मा है तो तापमान में परिवर्तन होगा,

$$ \begin{aligned} & \Delta \theta=\frac{\Delta U}{m s}=\frac{4 \pi T\left(R^{2}-N r^{2}\right)}{\frac{4}{3} \pi R^{3} \rho s}, \text { where } \rho \text { is the density. } \ & \therefore \Delta \theta=\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{r^{2}}{R^{3}} N\right) \ & =\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{r^{2} R^{3}}{R^{3} r^{3}}\right)=\frac{3 T}{\rho s}\left(\frac{1}{R}-\frac{1}{r}\right) \end{aligned} $$

10.20 बूंद वाष्प से अधिक होता है अगर पानी दबाव वाष्प-दबाव से ज्यादा हो। परत दबाव (पानी)

$$ \begin{aligned} & p=\frac{2 T}{r}=2.33 \times 10^{3} \mathrm{~Pa} \ \end{aligned} $$

कृपया अपनी सहायता के लिए किसी अन्य संबंधित विषय में संक्षेप संदेश प्रदान करें।

यदि $d^{\prime}$ बराबर होता है अतिमोलकुलीय दूरी, तो $$ \begin{aligned} & d^{3}=\left(3 \times 1601 \times 10^{-29}\right) \mathrm{m}^{3} \ & \therefore \quad d^{\prime}=(30 \times 1601)^{1 / 3} \times 10^{-10} \mathrm{~m} \ & =36.3 \times 10^{-10} \mathrm{~m} \end{aligned} $$

(डी) $F\left(d^{\prime}-d\right)=\mathrm{u} \Rightarrow F=\frac{u}{d^{\prime}-d}=\frac{6.8 \times 10^{-20}}{(36.3-3.1) \times 10^{-10}}=0.2048 \times 10^{-10} \mathrm{~N}$

(ई) $\quad F / d=\frac{0.2048 \times 10^{-10}}{3.1 \times 10^{-10}}=0.066 \mathrm{~N} \mathrm{~m}^{-1}=6.6 \times 10^{-2} \mathrm{~N} \mathrm{~m}^{-1}$

10.23 बैलून में दबाव $P_{i}$ हो और बाहरी दबाव $P_{\mathrm{o}}$ $P_{i}-P_{o}=\frac{2 \gamma}{r}$

हवा को एक आदर्श गैस मानते हुए

$P_{i} V=n_{i} R T_{i}$ यहाँ $V$ बैलून के अंदर हवा का आयाम है, $n_{\mathrm{i}}$ अंदर की मोलों की संख्या है और $T_{i}$ अंदर का तापमान है, और $P_{o} V=n_{o} R T_{o}$ यहाँ $\mathrm{V}$ वह हवा का आयाम है जो हटाई गई है और $n_{\mathrm{o}}$ उन मोलों की संख्या है जिन्होंने जगह बनाई है और $T_{\mathrm{o}}$ बाहरी तापमान है।

$n_{\mathrm{i}}=\frac{P_i V}{R T_{i}}=\frac{M_i}{M_A}$ यहाँ $M_i$ बालून के अंदर हवा की मास है और $M_A$ हवा का मौलिक मास है और $n_{\mathrm{o}}=\frac{P_{O} V}{R T_{O}}=\frac{M_{O}}{M_{A}}$ यहाँ $M_{\mathrm{o}}$ बाहरी हवा की मास है जो हटाई गई है। यदि $W$ वह भार है जिसे वह उठा सकता है, तो $W+M_{i} g=M_{o} g$ $\Rightarrow W=M_{o} g-M_{i} g$

हवा में $21 \% O_2$ और $79 \% N_2$ है

$\therefore$ हवा का मौलिक मास $M_{\mathrm{A}}=0.21 \times 32+0.79 \times 28=28.84 \mathrm{~g}$.

$\Rightarrow W=\frac{M_{A} V}{R}\left(\frac{P_{O}}{T_{o}}-\frac{P_{i}}{T_{i}}\right) g$

$=\frac{0.02884 \times \frac{4}{3} \pi \times 8^{3} \times 9.8}{8.314}\left(\frac{1.013 \times 10^{5}}{293}-\frac{1.013 \times 10^{5}}{333}-\frac{2 \times 5}{8 \times 313}\right) \mathrm{N}$ $\frac{0.02884 \times \frac{4}{3} \pi \times 8^{3}}{8.314} \times 1.013 \times 10^{5}\left(\frac{1}{293}-\frac{1}{333}\right) \times 9.8 \mathrm{~N}$

$=3044.2 \mathrm{~N}$.