अध्याय 13 किनेटिक सिद्धांत (Adhyay 13 Kinetik Siddhant)
अध्याय 13
क्रियाशीलता सिद्धांत
MCQ I
13.1 एक घनक्षेत्र (जिसके पैमाने आड़ी परिपत्रीका + आंशिक परिपत्रीका निर्मित होती है) एनटीपी पर एक आदर्श गैस सम्मिलित है। घनक्षेत्र को हवाई जहाज द्वारा उठाया जा रहा है, जो आंशिक दिशा में $500 \mathrm{~मी} \mathrm{~सेकंद}^{-1}$ की गति से चल रहा है। वस्त्रित ध्यानसे स्तंभ में सुचरिताओं के दबाव को हम द्वारा देखा जाता है
(क) वज़ वार्म्स की $500 \mathrm{~मी} \mathrm{~सेकंद}^{-1}$ से बहुत कम है, इसलिए वही रहेगा।
(ख) संपूर्ण वस्त्र संपूर्णता के बावजूद वज़ गाज़ के संबंधीय गति और दीवारों के बीच अपेक्षित गति को प्रभावित नहीं करती है, इसलिए वही रहेगा।
(स) $v^2_{r m s}+(500)^2) / v^2_{r m s}$ के बराबर अनुपात में बढ़ेगा, जहां $v_{r m s}$ मूल माध्यमिक वर्गमूल वेग था।
(द) वस्त्र की ऊर्ध्वाधर दीवार और नीचे की दीवार के ऊपरी दीवार पर भिन्न होगा।
13.2 एक आदर्श गैस का 1 मोल $300 \mathrm{~केल्विन}$ में एक घनद्विंदीय व्यास $V$ में समायुक्त है (आचरण 13.1)। व्यास का एक चेहरा (EFGH) ऐसा मांग है जो इस पर प्रभावित होने वाले किसी भी गैस अणु को पूरी तरह अवशोषित करता है। किसी भी समय पर,
(क) EFGH पर दबाव शून्य होगा।
(ख) सभी चेहरों पर दबाव समान होगा।
(ग) EFGH का दबाव ABCD पर दबाव का दोगुना होगा।
(घ) EFGH पर दबाव ABCD पर दबाव के हर्फ्बी होगा।
 आचरण 13.1
आचरण 13.1
13.3 बॉयल का नियम एक
(क) अधिगमी अवधि प्रक्रिया के लिए लागू होता है।
(ख) समस्थ अवधि प्रक्रिया के लिए लागू होता है।
(ग) नियमित दबाव प्रक्रिया के लिए लागू होता है।
(घ) समस्थ आवृत्ति प्रक्रिया के लिए लागू होता है।
13.4 एक आदर्श गैस समायुक्त एक घनक्षेत्र उच्च स्थान पर है और उसमें एक पिस्टन है जिसका मास $M$ है और जो घर्षण के बिना ऊपर या नीचे जा सकता है (आचरण 13.2)। यदि ऊष्मा बढ़ाई जाती है,
 आचरण 13.2
आचरण 13.2
13.5 दिए गए भौतिक गैस के एक निर्दिष्ट मास के लिए आयताकार तापमान आदर्श गैस बनाया गया चित्र 13.3 में दिखाए जा रहे हैं। रिश्ता के बारे में क्या निष्कर्ष निकाला जा सकता है बीना $P_1$ और $P_2$ के?
 आचरण 13.3
आचरण 13.3
13.6 एक बॉक्स में 1 मोल $\mathrm{H}_{2}$ गैस $V=1.00 \mathrm{~मी}^{3}$ और $T=300 \mathrm{~केल्विन}$ पर समायुक्त है। गैस को $T=3000 \mathrm{~केल्विन}$ तापमान पर गर्म किया जाता है और गैस को हाइड्रोजन अणुओं का एक गैस में परिणामस्वरूप बदल जाता है। अंतिम दबाव होगा (सभी गैस को आदर्श मानते हुए)
(क) आदिमानी दबाव के समान।
(ख) 2 गुना आदिमानी दबाव।
(ग) 10 गुना आदिमानी दबाव।
(घ) 20 गुना आदिमानी दबाव।
13.7 एक वस्तु $V$ आयताकार एक मिश्रण को समायुक्त है, 1 मोल हाइड्रोजन और 1 मोल ऑक्सीजन (दोनों आदर्श माने गए)। $f_{1}(v) d v$, को निर्देशित करता है, इससे अर्थात वे क्षेत्रों के बीच गति के साथ $v$ और $(v+d v)$ के बीच अवधि की अणुओं का अनुपात। $f_{2}(v) d v$, इसी तरह के लिए, ऑक्सीजन के बारे में दिया है। फिर
(क) $f_{1}(v)+f_{2}(v)=f(v)$ मैक्सवेल के वितरण कानून का पालन करता है।
वस्तुनिष्ठ आंकुड़ा: (बी) $f_{1}(v), f_{2}(v)$ आगणन स्वतंत्रता की अवहेलनिका का पालन करेंगे।
(सी) ना $f_{1}(v)$, ना ही $f_{2}(v)$ मैक्सवेल की वितरण का पालन करेंगे।
(डी) $f_{2}(v)$ और $f_{1}(v)$ एक समान होंगे।
13.8 एक फूली हुई रबर की गुब्बारा एक आदर्श गैस को धारण करती है, जिसमें एक मोल आदर्श गैस होती है, इसमें एक दबाव $p$, आयतन $V$ और तापमान $T$ होता है। यदि तापमान $1.1 \mathrm{~T}$ हो जाता है, और आयतन $1.05 \mathrm{~V}$ को बढ़ा दिया जाता है, तो अंतिम दबाव होगा
(अ) $1.1 p$
(बी) $p$
(सी) $p$ से कम
(डी) $p$ और 1.1 के बीच।
MCQ II
13.9 ABCDEFGH एक इन्सुलेटर बना हुआ खोखला क्यूब है (रेखा 13.4)। चेहरा $A B C D$ पर धारीदार आर्द्रता है। क्यूब के अंदर, हमें आयोनाइज्ड हाइड्रोजन है।
दबाव के लिए सामान्य किनेटिक सिद्धांती अभिव्यक्ति
 रेखा 13.4
रेखा 13.4
(अ) मान्य होगा।
(बी) मान्य नहीं होगा क्योंकि आयों को संघर्ष करने की दीवारों के साथ परेशानियों के अतिरिक्त बलों का अनुभव होगा।
(सी) मान्य नहीं होगा क्योंकि दीवारों से बाधाएं अपेक्षाकृत अपेक्षाकृत नहीं होंगी।
(डी) मान्य नहीं होगा क्योंकि ऐसा क्योंकि ऐसा सिद्धांतिक खो जाता है।
13.10 हाइड्रोजन जैसे द्वैपरीय अणुओं के पास संचारणात्मक और घुमावी गति के कारण ऊर्जा होती है। किनेटिक सिद्धांत में समीकरण से $p V=\frac{2}{3} E, \mathrm{E}$ होता है (अ) इकाई आयतन प्रति ऊर्जा।
(बी) केवल संचारणात्मक भाग के कारण, यहाँ तक कि घुमावी ऊर्जा त्रिषंगीय ऊर्जा की तुलना में बहुत छोटी होती है।
(सी) केवल संचारणात्मक भाग की ऊर्जा, क्योंकि दीवार से संघर्ष के दौरान दाब परिवर्तन से संबंधित होती है।
(डी) संचारणात्मक ऊर्जा का प्रकार क्योंकि अणुओं की घुमावी ऊर्जा किसी भी संकेत के तुलना में रह सकती है और इसका औसत सभी अणुओं पर शून्य होता है।
13.11 एक द्वैपरीय अणु में, एक दिए गए तापमान पर घूमने की ऊर्जा
(अ) मैक्सवेल की वितरण का पालन करता है।
(बी) सभी अणुओं के लिए एक ही मान रखता है।
(सी) प्रत्येक अणु के लिए संचारणात्मक ऊर्जा से बराबर होता है।
(डी) प्रत्येक अणु के लिए संचारणात्मक ऊर्जा का $(2 / 3)$ वाँ भाग होता है।
13.12 निम्नलिखित प्रतिमाओं में से कौन-सा प्रतिमा (रेखा 13.5) आदर्श गैस व्यवहार की चित्रित करता है?
(अ)
(सी)
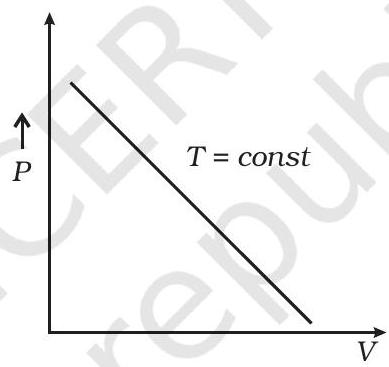
(बी)
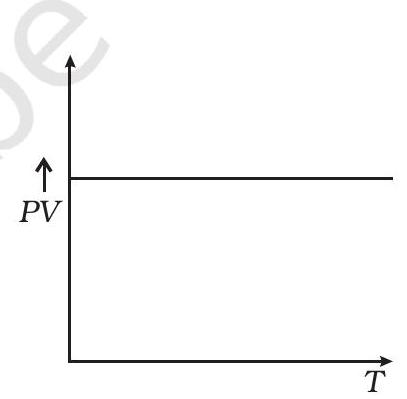
(डी)
रेखा 13.5
13.13 जब एक आदर्श गैस को संशोधित रूप से अछेदित किया जाता है, तो इसका तापमान बढ़ता है: चंद्रमा के मोलेक्यूल न्यूनतम किनेटिक ऊर्जा से अधिक होते हैं। किनेटिक ऊर्जा बढ़ती है,
(अ) केवल दीवार के चलते टक्कर के कारण।
(बी) दीवार के पूरे संघर्ष के कारण।
(c) क्योंकि अणुओं की गति अपने आंतरिक स्रोतों में तेजी से बढ़ती है।
(d) क्योंकि अणुओं के बीच ऊर्जा का पुनर्वितरण हो जाता है।
VSA
13.14 सोने में $39.4 \mathrm{~g}$ के अणुओं की संख्या की गणना करें। सोने का मौलर Molar द्रव्यमान $197 \mathrm{~g} \mathrm{~mole}^{-1}$ है।
13.15 $27^{\circ} \mathrm{C}, 1 \mathrm{~atm}$ पर एक निर्धारित द्रव्यमान वाले गैस का आयतन $100 \mathrm{cc}$ है। इसका आयतन $327^{\circ} \mathrm{C}$ पर क्या होगा?
13.16 निर्धारित द्रव्यमान वाले एक गैस के अणुओं की झूलती औसत गति $27^{\circ} \mathrm{C}$ और 1.00 वायुमंडलीय दबाव पर $100 \mathrm{~m} \mathrm{~s}^{-1}$ होती है। गैस के अणुओं की झूलती औसत गति $127^{\circ} \mathrm{C}$ और 2.0 वायुमंडलीय दबाव पर क्या होगी?
13.17 एक गैस की दो अणुओं की गति $9 \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$ और $1 \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$ है। इन अणुओं की झूलती औसत गति क्या होगी?
13.18 एक गैस मिश्रण में 2.0 मोल ऑक्सीजन और 4.0 मोल नीयॉन होते हैं जिनकी तापमान T होती है। सभी विव्रेसणात्मक स्थितियों को ध्यान न देते हुए, प्रणाली का कुल आंतरिक ऊर्जा की गणना करें। (ऑक्सीजन के पास दो परिवर्तनात्मक विभ्रान्ति साध्य होती हैं।)
13.19 मोलार ब्यास के $1 \mathrm{~A}$ और $2 \mathrm{~A}$ मोलेशुल वाले दो गैसों की औसत मुक्त मार्गों का अनुपात गणना करें। गैस को ताप, दबाव और आयतन की एक जैसी शर्तों के तहत माना जा सकता है।
| $V_{1}$ | $V_{2}$ |
|---|---|
| $\mu_{1}, p_{1}$ | $\mu_{2}$, |
| $p_{2}$ |
चित्र 13.6
SA
13.20 चित्र 13.6 में दिखाए गए कंटेनर में दो अधरों को अलग किया जाता है, जिनकी आयतन एक होती है $V_{1}=2.0$ लीटर और $V_{2}=3.0$ लीटर है। कमरों में प्रेसर शामिल होते हैं $\mu_{1}=4.0$ और $\mu_{2}=5.0$ मोल एक गैस के दबाव $p_{1}=1.00 \mathrm{~atm}$ और $p_{2}=2.00 \mathrm{~atm}$ होते हैं। विभाजन हटाए जाने के बाद और मिश्रण प्राप्त करने के बाद दबाव गणना करें।
13.21 एक गैस मिश्रण में प्रकार A, B और C के अणु होते हैं जिनका द्रव्यमान $m_{A}>m_{B}>m_{C}$ होता है। (a) औसत K.E. के क्रम को क्रमशः कम करें, (b) rms गति को क्रमशः कम करें।
13.22 हमारे पास $3 \mathrm{~cm}$ के कक्ष में नितीपुस्तक मौल $0.5 \mathrm{~g}$ हाइड्रोजन गैस है। गैस को संकुचित किया जाता है जबकि तापमान को स्थिर रखते हुए आखिरी दबाव $100 \mathrm{~atm}$ होता है। क्या आखिरी स्थिति में आदर्श गेस कानून को मान्यता दी जा सकती है? (हाइड्रोजन अणुओं को $1 \stackrel{\circ}{\AA}$ त्रिज्या के स्फेरों के रूप में माना जा सकता है।)
13.23 जब साइकिल टायर में हवा पंप की जाती है, तो हवा का आयतन और दबाव दोनों बढ़ जाते हैं। इस मामले में बॉयल का नियम क्या होता है?
13.24 एक गुब्बारे में $5.0 \mathrm{~g}$ परमाणु हीलियम होते हैं जो $7^{\circ} \mathrm{C}$ पर होते हैं। गुब्बारे में हीलियम के परमाणुओं की संख्या गणना करें,
(a) प्रणाली का कुल आंतरिक ऊर्जा।
13.25 NTP पर $1 \mathrm{cc}$ हाइड्रोजन गैस के मोलेक्यूलों की स्वतंत्रता की गणना करें।
13.26 एक उत्सर्जित बरतन जिसमें मोलर भार मांग $m$ वाली एकात्मक गैस है, वेग $v_{o}$ के साथ चल रहा है। अगर बरतन को अचानक रोक दिया जाता है, तो तापमान में परिवर्तन निकालें।
LA
13.27 क्यों होती है
(a) चांद पर कोई वातावरण नहीं होता है।
(b) ऊंचाई के साथ तापमान घटना होता है।
13.28 एक आदर्श गैस को निम्नलिखित वेग वितरण के साथ मानें।
| वेग $(\mathrm{m} / \mathrm{s})$ | अवधारित कक्षा |
|---|---|
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(i) $V_{r m s}$ और तापमान $T$ की गणना करें। $\left(m=3.0 \times 10^{-26} \mathrm{~kg}\right)$
(ii) यदि सभी वेग $1000 \mathrm{~m} / \mathrm{s}$ वाले अणु सिस्टम से निकल जाते हैं, तो नया $V_{r m s}$ और इसलिए $T$ का गणना करें।
13.29 दस छोटे विमान $150 \mathrm{~km} / \mathrm{h}$ की गति से अधिकांश अंधकार में उड़ रहे हैं एक ऐसे वायु अंतरिक्ष में, जो $20 \times 20 \times 1.5 \mathrm{~km}^{3}$ के आयताकार मात्रा में है। आप उनमें से एक में हैं, जो इस स्थान पर यातायात कर रहा है, और आपको यह भी पता नहीं है कि अन्य विमान कहां हैं। औसतन आपके विमान के पास कब नजदीकी संपर्क होने के बीच कितना समय बितेगा। इस अंदाजी के लिए मान लें कि विमान के आसपास की सुरक्षा क्षेत्र को $10 \mathrm{~m}$ के त्रिज्या वाले गोलकार के द्वारा उपग्रहीत किया जा सकता है।
13.30 एक $1.00 \mathrm{~m}^{3}$ का बक्सा $1.50 \mathrm{~atm}$ दबाव के साथ $300 \mathrm{~K}$ पर नाइट्रोजन से भरा है। बक्से में एक $0.010 \mathrm{~mm}^{2}$ क्षेत्र है। अगर बाहरी दबाव $1 \mathrm{~atm}$ है, तो दबाव को $0.10 \mathrm{~atm}$ से कम करने के लिए कितना समय लगेगा।
13.31 एक आयताकार लकड़ी का ब्लॉक जो गति $v_{0}$ के साथ निरंतर गैस में चल रहा है, तापमान $T$ और भारीतम घनत्व $\rho$ के साथ। मानें कि वेग $x$-अक्ष के संगत है और वेग यात्रा के अपरिसीमित रेखीय क्षेत्र $A$ है। दिखाएं कि ब्लॉक पर खींच का बल $4 \rho A v_{o} \sqrt{\frac{k T}{m}}$ होता है, यहां $m$ गैस अणु का भार है।
समाधान 13
13.1 (ब)
विचारण के लिए टिप्पणी: यह संगत गति और जब टक्कर होती है, तो यह परिवर्तन होने वाली संगत वेग होती है।
13.2 (ड)
विचारण के लिए टिप्पणी: हम आमतौर पर विचार करते हैं कि आदर्श मामले में, प्रत्येक टक्कर अपनी सामान्य संगत गति के दोगुना चमत्कार करती है। मुख ईएफजीएच पर, यह केवल आधा चमत्कार करती है।
13.3 (ब)
13.4 (क) यह एक स्थिर दबाव $(p=M g / A)$ व्यवस्था है।
13.5 (अ)
13.6 (ड)
विचारण के लिए टिप्पणी: सामान्यतः हम आपत्ति यह प्रदर्शित करते हैं कि पूर्ण गैस कानून में अणुओं के उल्लेख को थोड़ा मज़बूती से दिखाया जाता है।
13.7 (ब)
टिप्पणी: मिश्रण में, औसत गति के समानरूप माध्यामिक ऊर्जा होती हैं। इसलिए, वेग में वितरण काफी अलग होता है।
13.8 $(\mathrm{ड})$
चर्चा के लिए टिप्पणी: इस अध्याय में, हमने स्थिर दबाव और स्थिर आयतन स्थितियों पर चर्चा की है लेकिन वास्तविक जीवन में ऐसी कई स्थितियाँ होती हैं जहाँ दोनों बदलते हैं। यदि सतहें कठोर होतीं, तो p $पर 1.1 p वृद्धि होतीं। हालांकि, जैसे दबाव बढ़ता है, V भी बढ़ता है इस प्रकार कि p v अंततः 1.1 R T होता है जबकि pₓₖₐलₐ > p और Vₓₖₐलₐ > V। इसलिए (d)।
13.9 (b), (d)
13.10 (c)
13.11 (a), (d)
टिप्पणी: इसका शिक्षण होता है कि <K.E. of translation > = $(3 / 2) R T, <$ Rotational energy $>=R T।>इन दोनों दिस्त्री में की वितरण अपेक्षाकृत एक दूसरे से अखंडता नहीं रखी जाती है। वे अस्वतंत्र रूप से मैक्सवेलियन हैं।
13.12 (a), (c)
13.13 (a)
टिप्पणी: संवेदनशील रूप से, छात्रों को आमतौर पर स्पष्ट नहीं होता है कि एक चलता वस्तु के साथ संवेदनशील टकराव में इसकी ऊर्जा में परिवर्तन होता है।
13.14 इसलिए सोने का मौलौरी मास $197 \mathrm{~g} \mathrm{~mole}^{-1}$ है, परमाणुओं की संख्या $=6.0 \times 10^{23}$
इसलिए $39.4 \mathrm{~g}$ में परमाणुओं की संख्या $=\frac{6.0 \times 10^{23} \times 39.4}{197}=1.2 \times 10^{23}$
13.15 $P$ को स्थिर रखकर हमें मिलता है
$V_{2}=\frac{V_{1} T_{2}}{T_{1}}=\frac{100 \times 600}{300}=200 \mathrm{cc}$
13.16 $\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}$
$\frac{V_{1}}{V_{2}}=\frac{P_{2} T_{1}}{P_{1} T_{2}}=\frac{2 \times 300}{400}=\frac{3}{2}$
$P_{1}=\frac{1}{3} \frac{M}{V_{1}} c_{1}^{-2} ; \quad P_{2}=\frac{1}{3} \frac{M}{V_{2}} c_{2}^{-2}$
$\therefore c_{2}{ }^{2}=c_{1}{ }^{2} \times \frac{V_{2}}{V_{1}} \times \frac{P_{2}}{P_{1}}$
$=(100)^{2} \times \frac{2}{3} \times 2$
$c_{2}=\frac{200}{\sqrt{3}} \mathrm{~m} \mathrm{~s}^{-1}$
13.17 $v_{r m s}=\sqrt{\frac{v_{1}^{2}+v_{2}^{2}}{2}}$
$=\sqrt{\frac{\left(9 \times 10^{6}\right)^{2}+\left(1 \times 10^{6}\right)^{2}}{2}}$
$=\sqrt{\frac{(81+1) \times 10^{12}}{2}}=\sqrt{41} \times 10^{6} \mathrm{~m} \mathrm{~s}^{-1}$.
13.18 $\mathrm{O}_{2}$ का 5 डिग्री की स्वतंत्रता होती है। इसलिए, प्रति मोल ऊर्जा $=\frac{5}{2} R T$
$\therefore$ 2 मोल के लिए ऊर्जा $=5 R T$
नीओन का 3 डिग्री की स्वतंत्रता होती है इसलिए प्रति मोल ऊर्जा $=\frac{3}{2} R T$
$\therefore$ 4 मोल नीओन के लिए ऊर्जा $=4 \times \frac{3}{2} R T=6 R T$
$\therefore$ कुल ऊर्जा $=11$ RT.
उदाः समस्याएँ-भौतिकी
13.19 $l \alpha \frac{1}{d^{2}}$
$d_{1}=1 \stackrel{o}{A} \quad \alpha_{2}=2 \stackrel{o}{\AA}$
$l_{1}: l_{2}=4: 1$
13.20 $V_1=2.0$ लीटर $V_2=3.0$ लीटर
$\mu_{1}=4.0$ मोल $\mu_{2}=5.0$ मोल
$P_1=1.00$ एटमस्फीयर $P_2=2.00$ एटमस्फीयर
$P_{1} V_{1}=\mu_{1} R T_{1} \quad P_{2} V_{2}=\mu_{2} R T_{2}$
$\mu=\mu_{1}+\mu_{2} \quad V=V_{1} V_{2}$
1 मोल के लिए $P V=\frac{2}{3} E$
$\mu_{1}$ मोल के लिए $P_{1} V_{1}=\frac{2}{3} \mu_{1} E_{1}$
$\mu_{2}$ मोल के लिए $P_{2} V_{2}=\frac{2}{3} \mu_{2} E_{2}$
कुल ऊर्जा $\left(\mu_{1} E_{1}+\mu_{2} E_{2}\right)=\frac{3}{2}\left(P_{1} V_{1}+P_{2} V_{2}\right)$
$P V=\frac{2}{3} E_{\text {total }}=\frac{2}{3} \mu E_{\text {per mole }}$
कंटेंट का ही संस्करण क्या है: $P\left(V_{1}+V_{2}\right)=\frac{2}{3} \times \frac{3}{2}\left(P_{1} V_{1}+P_{2} V_{2}\right)$
$P=\frac{P_{1} V_{1}+P_{2} V_{2}}{V_{1}+V_{2}}$
$=\left(\frac{1.00 \times 2.0+2.00 \times 3.0}{2.0+3.0}\right) \mathrm{एटीएम}$
$=\frac{8.0}{5.0}=1.60 \mathrm{~एटीएम}$.
टिप्पणी: मार्क किए गए समीकरण द्वारा प्रतिष्ठान गैस के इस रूप का उपयोग अधिभौतिक परिवर्तनों के लिए बहुत उपयोगी हो जाता है।
13.21 औसत केनेटिक ऊर्जा स्थिति की गर्मी और दबाव की स्थितियों के समान होगी
$v_{r m s} \alpha \frac{1}{\sqrt{m}}$
$m_{A}>m_{B}>m_{c}$
$v_{C}>v_{B}>v_{A}$
13.22 हमारे पास $0.25 \times 6 \times 10^{23}$ अणु हैं, प्रत्येक का आयतन $10^{-30} \mathrm{~मीटर}^{3}$ है।
अणु का आयतन $=2.5 \times 10^{-7} \mathrm{~मीटर}^{3}$
यदि आदर्श वायु का नियम मान्य होता है।
अंतिम आयतन $=\frac{V_{i n}}{100}=\frac{(3)^{3} \times 10^{-6}}{100} \approx 2.7 \times 10^{-7} \mathrm{~मीटर}^{3}$
जो लगभग अणु का आयतन है। इसलिए, आंतरणीय बलों को नजरअंदाज नहीं किया जा सकता है। इसलिए आदर्श वायु स्थिति पालन नहीं करती है।
13.23 जब हवा पंप किया जाता है, तो अधिक अणु पंप किए जाते हैं। बॉयल का नियम अवस्था के लिए बतलाया जाता है जहां अणु संख्या स्थिर रहती है।
13.24 $\mu=5.0$
$T=280 \mathrm{~केल्विन}$
अणु की संख्या $=\mu N_{A}=5.0 \times 6.02 \times 10^{23}$
$$ =30 \times 10^{23} $$
प्रत्येक अणु की औसत केनेटिक ऊर्जा $=\frac{3}{2} k T$
$\therefore$ कुल आंतरिक ऊर्जा $=\frac{3}{2} k T \times N$
$$ \begin{aligned} & =\frac{3}{2} \times 30 \times 10^{23} \times 1.38 \times 10^{-23} \times 280 \ & =1.74 \times 10^{4} \mathrm{~जूल} \end{aligned} $$
13.25 NTP पर गैस के 1 ग्राम मोल द्वारा जितनी थानी जाती है $=22400 \mathrm{सीसी}$
$\therefore$ 1 सीसी वाले हाइड्रोजन में अणुओं की संख्या
$$ =\frac{6.023 \times 10^{23}}{22400}=2.688 \times 10^{19} $$
प्रत्येक द्वायी अणु के 5 स्वतंत्रता अवस्थाएं होती हैं, हाइड्रोजन द्वायी होते हुए भी 5 स्वतंत्रता अवस्थाएं होती हैं, $\therefore$ कुल स्वतंत्रता अवस्थाओं की संख्या $=5 \times 2.688 \times 10^{19}$
13.26 गैस की किनेटिक ऊर्जा की हानि $=\Delta E=\frac{1}{2}(m n) v_{o}{ }^{2}$
$$ =1.344 \times 10^{20} $$
जहां $n=$ आयतनों की संख्या।
अगर इसकी तापमान $\Delta T$ बदलती है, तो
$n \frac{3}{2} R \Delta T=\frac{1}{2} m n v_{o}^{2} . \quad \therefore \Delta T=\frac{m v_{o}{ }^{2}}{3 R}$
13.27 प्रकृति की ओर से चंद्रमा में कम गुरुत्वाकर्षण बल होता है और इसलिए बाहरी वेग कम होता है। सूर्य से देखा गया चंद्रमा पृथ्वी के आस-पास है इसलिए चंद्रमा की एक इकाई क्षेत्र के लिए पृथ्वी की तरही ही गर्मी प्रति इकाई की मात्रा होती है। हवा के अणुओं की बहुत विस्तृत गति होती है। हालांकि हवा के अणुओं की औसत गति चंद्रमा पर बाहरी वेग से छोटी होती है, एक प्रमुख संख्या के अणुओं की गति बाहरी वेग से अधिक होती है और वे भागते हैं। अब बाकी अणुओं को स्थिरता की गतिविधि के लिए गति वितरण करते हैं आवेगीय सन्तुलन के लिए। फिर भी एक प्रमुख संख्या के अणु अपनी गति बाहरी वेग से अधिक होने के कारण भागते हैं। इसलिए, बहुत समय तक चंद्रमा ने अपना बहुतायत से वायुमंडल खो दिया है।
भाषा: hi
किन्तु भौतिक वातावरण में (at $300 \mathrm{~K}$), वेग का ज्ञात प्राथमिकी रूप से $V_{\text {rms}}=\sqrt{\frac{3 k T}{m}}=\sqrt{\frac{3 \times 1.38 \times 10^{-23} \times 300}{7.3 \times 10^{-26}}}=1.7 \mathrm{~km} / \mathrm{s}$ होता है। चंद्रमा के लिए $\mathrm{V}_{\text {esc }} = 4.6 \mathrm{~km} / \mathrm{s}$ है।
(बी) जब मोलेक्यूल ऊँचाई पर चलते हैं, तो उनकी स्थानिक ऊर्जा बढ़ती है और इसलिए किनेटिक ऊर्जा घटती है और इसलिए तापमान भी कम होता है।
ऊँचाई के साथ अधिक आकार उपलब्ध होता है और गैस फैलती है, इसलिए कुछ शीतलन होता है।
13.28 (इस समस्या का उद्देश्य व्यापन से शीतलन के बारे में एक विचार देना है)
(आई)
$$ \begin{aligned} & V_{\text{rms}}^{2}=\frac{n_{i}v_{i}^{2}}{n_{i}} \ & =\frac{10 \times (200)^{2} + 20 \times (400)^{2} + 40 \times (600)^{2} + 20 \times (800)^{2} + 10 \times (1000)^{2}}{100} \ & = \frac{10 \times 100^{2} \times (1 \times 4 + 2 \times 16 + 4 \times 36 + 2 \times 64 + 1 \times 100)}{100} \ & = 1000 \times (4 + 32 + 144 + 128 + 100) = 408 \times 1000 \mathrm{~m}^{2} / \mathrm{s}^{2} \end{aligned} $$
$$ \begin{aligned} & \therefore v_{\text{rms}} = 639 \mathrm{~m} / \mathrm{s} \ & \frac{1}{2}m v_{\text{rms}}^{2} = \frac{3}{2}kT \ & \therefore T=\frac{1}{3}\frac{m v_{\text{rms}}^{2}}{k}= \frac{1}{3} \times \frac{3.0 \times 10^{-26} \times 4.08 \times 10^{5}}{1.38 \times 10^{-23}} \ & \quad=2.96 \times 10^{2} \mathrm{~K}=296 \mathrm{~K} \end{aligned} $$
(ii) $V_{\text{rms}}^{2}=\frac{10 \times (200)^{2} + 20 \times (400)^{2} + 40 \times (600)^{2} + 20 \times (800)^{2}}{90}$
$$ \begin{aligned} & = \frac{10 \times 100^{2} \times (1 \times 4 + 2 \times 16 + 4 \times 36 + 2 \times 64)}{90} \ & = 10000 \times \frac{308}{9} = 342 \times 1000 \mathrm{~m}^{2} / \mathrm{s}^{2} \ v_{\text{rms}} & = 584 \mathrm{~m} / \mathrm{s} \ T & = \frac{1}{3}\frac{m V_{\text{rms}}^{2}}{k} = 248 \mathrm{~K} \end{aligned} $$
13.29 समय $t=\frac{\lambda}{v}$
$\lambda=\frac{1}{\sqrt{2}\pi d^{2}n}, d=$ व्यास और $n=$ संख्या घनत्व
$n = \frac{N}{V} = \frac{10}{20 \times 20 \times 1.5} = 0.0167 \mathrm{~km}^{-3}$
$t = \frac{1}{\sqrt{2}\pi d^{2}(N / V) \times v}$
$= \frac{1}{1.414 \times 3.14 \times (20)^{2} \times 0.0167 \times 10^{-3} \times 150}$
$= 225 \mathrm{~h}$
13.30 $V_{1x}=$ बॉक्स के अंदर के यातायात की गति $x$ दिशा में
$n_{1}=$ इकाई आयतन के भीतर पारमाणुओं की संख्या
$\Delta t$ के दौरान, दीवार के साथ मोड़ रही कणों की संख्या, यदि वे $\left(V_{1x} \Delta t\right)$ दूरी के भीतर हों तो होगी। यदि $a=$ दीवार का क्षेत्र है। $\Delta t$ समय में टक्राए गए कणों की संख्या
$=\frac{1}{2} n_{i}\left(V_{i x} \Delta t\right) a$ (दीवार की ओर गति के कारण 1/2 का अंश)।
सामान्यतः, छिद्र के मुकाबले दीवार बहुत बड़ा होता है क्योंकि गैस विद्युत के कारण।
$\therefore V_{1x}^2 + V_{1y} + V_1^2 = V^2_{rms}$
$\therefore V_{1 x}^{2}=\frac{V^{2}{ }_{\text{rms}}}{3}$
$\frac{1}{2} m V^2_{\text{rms}}=\frac{3}{2} k T \Rightarrow V^2_{\text{rms}}=\frac{3 k T}{m}$
$\therefore V^{2}{ }_{1 x}=\frac{k T}{m}$
$\therefore$ समय $\Delta t$ में टकराने वाले कणों की संख्या $=\frac{1}{2} n_{1} \sqrt{\frac{k T}{m}} \Delta t a$। यदि टकराते हैं
संघर्ष साथ होकर गड्ढे के साथ टकराए, वे बहार जाते हैं। उसी तरह, बाहरी कण गड्ढे के साथ टकराए गए आंतरिक कण में चले जाएंगे।
$\therefore$ समय $\Delta t$ में नेट कण प्रवाह $\Delta t=\frac{1}{2}\left(n_{1}-n_{2}\right) \sqrt{\frac{k T}{m}} \Delta t a$ के बराबर है, क्योंकि आंतरिक और बाहरी में समान तापमान है।
$p V=\mu R T \Rightarrow \mu=\frac{P V}{R T}$
$n=\frac{\mu N_{A}}{V}=\frac{P N_{A}}{R T}$
कुछ समय $\tau$ बाद दबाव $p_{1}^{\prime}$ अंदर हो जाता है
$\therefore n_{1}^{\prime}=\frac{P_{1}^{\prime} N_{A}}{R T}$
$n_{1} V-n_{1}^{\prime} V=$ नंबर पार्टिकलों की संख्या जो बाहर चली गई है $=\frac{1}{2}\left(n_{1}-n_{2}\right) \sqrt{\frac{k T}{m}} \tau a$
$\therefore \frac{P_{1} N_{A}}{R T} V-\frac{P_{1}^{\prime} N_{A}}{R T} V=\frac{1}{2}\left(P_{1}-P_{2}\right) \frac{N_{A}}{R T} \sqrt{\frac{k T}{m}} \tau a$
$\therefore \tau=2\left(\frac{P_{1}-P_{1}^{\prime}}{P_{1}-P_{2}}\right) \frac{V}{a} \sqrt{\frac{m}{k T}}$
$=2\left(\frac{1.5-1.4}{1.5-1.0}\right) \frac{5 \times 1.00}{0.01 \times 10^{-6}} \sqrt{\frac{46.7 \times 10^{-27}}{1.38 \times 10^{-23} \times 300}}$
$=1.38 \times 10^{5} \mathrm{~s}$
13.31 $n=$ इकाई आयाम प्रति कक्षा के अणु
$v_{\text {rms }}=$ गैस के अणुओं की RMS गति
जब ब्लॉक गति $v_{o}$ के साथ चल रहा हो, तो अणुओं की साथ बलकि पर के प्रति गति $=v+v_{o}$ होती है
सीधे मुकाबले में, ब्लॉक को हर टक्कर पर अणुओं द्वारा जलाई गई गति
$$ =2 m\left(v+v_{o}\right) \text {, यहां } m=\text { अणु का मास. } $$
समय $\Delta t$ में टक्करों की संख्या $\Delta t=\frac{1}{2}\left(v+v_{o}\right) n \Delta t A$ होती है, यहां $\mathrm{A}=$ ब्लॉक के पार्श्व मुख के क्षेत्रफल है और $1 / 2$ का कारण अणु ब्लॉक की ओर रुखते हैं।
$\therefore$ समय $\Delta t$ में जब्त बल माथपान सतह से जलाई गई गति $m\left(v+v_{o}\right)^{2} n A \Delta t$ होती है
उसी तरह समय $\Delta t$ में जब्त बल पीछे सतह से जलाई गई गति $m\left(v-v_{o}\right)^{2} n A \Delta t$ होती है
$\therefore$ नेट बल (ड्रैग बल) $=\operatorname{mnA}\left[\left(v+v_{o}\right)-\left(v-v_{o}\right)^{2}\right]$ पीछे से
$$ =m n A\left(4 v v_{o}\right)=(4 m n A v) v_{o} $$
$$ =(4 \rho A v) v_{o} $$
हमारे पास $\frac{1}{2} m v^{2}=\frac{1}{2} k T \quad(v-$ वेग $x$-अक्ष की ओर $)$ है
इसलिए, $v=\sqrt{\frac{k T}{m}}$।
इस प्रकार ड्रैग $=4 \rho A \sqrt{\frac{k T}{m}} v_{0}$ होगा।





