अध्याय 3

सीधी रेखा में गति

MCQ I

3.1 चार ग्राफों में (चित्र 3.1), समय अंतराल $(O, T)$ पर औसत वेग वाइश्विकीय रूप से छोट जा सकता है जब छोट जाया जाता है। कौन सा है?

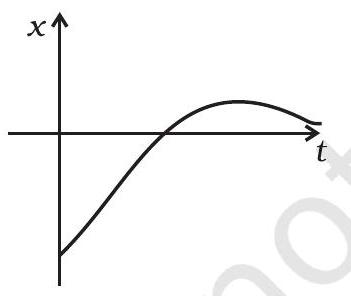
(a)

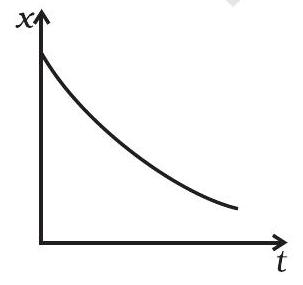
(c)

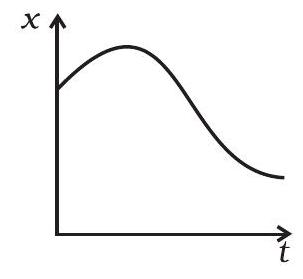
(b)

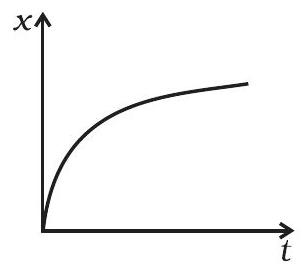
(d)

चित्र 3.1

3.2 लिफ्ट 8 वें मंजिल से आ रही है और 4 वें मंजिल तक पहुंचने के लिए है। सभी मात्राओं के लिए निचली मंजिल को मूल मानिए और सकारात्मक दिशा को समूची के लिए ऊपर की ओर लिया जाता है, इनमे से कौन सा सही है?

(a) $x<0, v<0, a>0$

(b) $x>0, v<0, a<0$

(c) $x>0, v<0, a>0$

(d) $x>0, v>0, a<0$

3.3 एक आयामी गति में, क्षणिक वेग $v$ को $0 \leq v<v_{0}$ मान लेते हैं।

(a) अंतर्वाल $T$ में स्थानांतरण हमेशा धनात्मक मान लिए जाने चाहिए।

(b) अंतर्वाल $T$ में स्थानांतरण $-v_{\mathrm{o}} \mathrm{T}<x<v_{\mathrm{o}} \mathrm{T}$ को पूरा करता है।

(c) त्वरण हमेशा एक धनात्मक संख्या होती है।

(d) गति के कोई चरम बिंदु नहीं होते हैं।

3.4 एक वाहन $V_{1}$ गति के साथ आधी दूरी $L$ तय करता है और बाकी अधीन दूरी $V_{2}$ गति के साथ, इसकी औसत वेग है

(a) $\frac{V_{1}+V_{2}}{2}$

(b) $\frac{2 V_{1}+V_{2}}{V_{1}+V_{2}}$

(c) $\frac{2 V_{1} V_{2}}{V_{1}+V_{2}}$

(d) $\frac{L\left(V_{1}+V_{2}\right)}{V_{1} V_{2}}$

3.5 एक कण का स्थानांतरण $x=(t-2)^{2}$ द्वारा दिया जाता है, जहां $x$ मीटर में है और $t$ सेकंड में। पहले 4 सेकंड में कण द्वारा चले गए दूरी है

(a) $4 \mathrm{~m}$

(b) $8 \mathrm{~मीटर}$

(c) $12 \mathrm{~मीटर}$

(d) $16 \mathrm{~मीटर}$

3.6 मेट्रो स्टेशन पर, एक लड़की एक रुके हुए एस्केलेटर पर चलती है, समय $t_{1}$ में। अगर वह एस्केलेटर पर स्थिर रहती है, तो एस्केलेटर उसे समय $t_{2}$ में ऊपर ले जाता है। चलती हुई एस्केलेटर पर चलने का समय होगा

(a) $\left(t_{1}+t_{2}\right) / 2$

(b) $t_{1} t_{2} /\left(t_{2}-t_{1}\right)$

(c) $t_{1} t_{2} /\left(t_{2}+t_{1}\right)$

(d) $t_{1}-t_{2}$

MCQ II

3.7 चित्र 3.2 में संज्ञा A के साथ संख्या B का अव्यवस्थित नाटकीय एक कण की गति का वर्णन करती है।

(a) चित्रित कहीं न कहीं बहुत जाती है समय को दिखा सकती है।

(b) अगर गति समान है तो वेग गति है।

(c) अगर गति समान है तो स्थानांतरण गति है।

(d) अगर गति नियमित त्रिगुणित है तो वेग गति है।

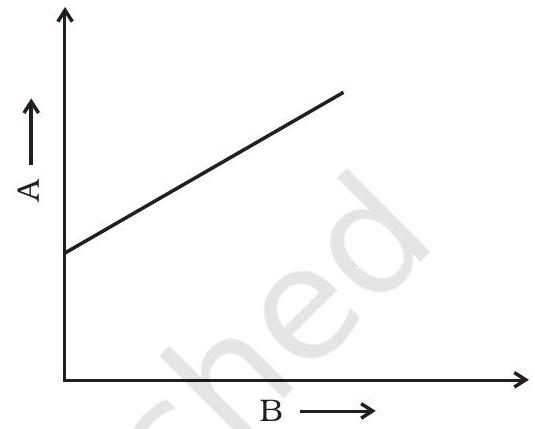
चित्र 3.2

3.8 चित्र 3.3 में $x$ के लिए $t$ का एक ग्राफ दिखाया गया है। नीचे से सही विकल्प चुनें।

(a) धारा $t=0$ पर आराम से छोड़ी गई।

(b) बी पर, त्वरण $a>0$ है।

(c) सी पर, वेग और त्वरण शून्य हैं।

(d) ए से डी तक गति के औसत वेग का मान सकारात्मक है।

(e) डी पर गति, ई पर गति से अधिक है।

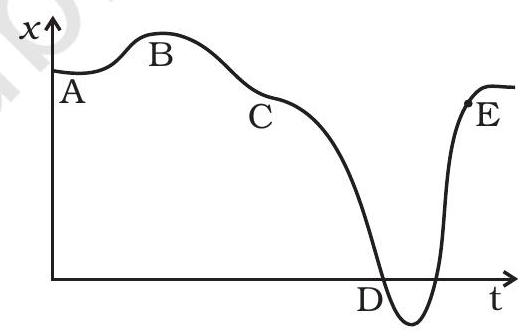
चित्र 3.3

3.9 एक आयामी गति के लिए, $x=t-\sin t$ से वर्णित एक अवस्था में

(a) $x(t)>0$ सभी $t>0$ के लिए।

(b) $v(\mathrm{t})>0$ सभी $t>0$ के लिए।

(c) $a(t)>0$ सभी $t>0$ के लिए।

(d) $v(\mathrm{t})$ 0 और 2 के बीच होता है।

3.10 एक धारण में एक स्प्रिंग का एक सिरा मान और दृढ़ समर्थन में चढ़ाया और छोड़ दिया जाता है।

(a) बस छोड़ा हुआ समय होने पर त्वरण का अभिकलनशीलता का मान अधिकतम होता है।

(b) समतावस्था स्थिति में होने पर त्वरण का अभिकलनशीलता का मान अधिकतम होता है।

(c) मास के समतावस्था स्थान पर तेज़ी अधिकतम होती है।

(d) गति सबसे कम होने पर स्थान का अभिकलनशीलता का मान हमेशा अधिकतम होता है।

3.11 एक गेंद को एक बहुत छोटे समय अंतराल के लिए एक बैट से मारकर उसे चुस्त रूप से पालटा जाता है। एक रेलवे कुशगर्त के दीवारों के बीच गति के समानांतर दिशा में $1 \mathrm{~m} / \mathrm{s}$ की गति से नीचे, पृथ्वी से देखा गया है।

(a) गेंद की गति हर 10 सेकंड में बदलती है।

(b) गेंद की गति हर 10 सेकंड में बदलती है।

(c) किसी भी 20 सेकंडी अंतराल में गेंद की औसत गति स्थिर होती है।

(d) गेंद का त्वरण ट्रेन से समान होता है।

VSA

3.12 चित्र 3.1 में दी गई ग्राफिक के विशेषता से मेल खाएँ।

ग्राफिक विशेषता

(a) (i) के लिए $v>0$ और $a<0$ सभी परिपूर्ण होता है।

(b) (ii) में $x>0$ हर बार रहता है और $v=0$ और $a=0$ के साथ एक बिंदु होता है।

(c) (iii) में $t>0$ के लिए शून्य स्थानांतर है।

(d) (iv) के लिए $v<0$ और $a>0$ सभी परिपूर्ण होता है।

3.13 एक यौनिक गतिरेखा खोखली हो रही है, जिस पर क्रिकेट गेंद सेंटिमीटर के या मीटर के रूप में बदलती है। इसकी वेगगति वक्र होगी। पत्रिका को बदले बिना प्राकृतिक संख्यानुक्रमित आकार का उपयोग करें।। उलटी मा।

3.14 एक एक-मात्रावधिक गति के उदाहरण दें, जहां

(a) पॉजिटिव $x$-दिशा में चल रहे कण समय-समय पर आराम से रुकता है और आगे बढ़ता है।

(b) पॉजिटिव $x$-दिशा में चल रहे कण समय-समय पर आराम से रुकता है और पीछे जाता है।

3.15 एक ऐसी गतिरेखा का उदाहरण दें जहां $x>0, v<0, a>0$ किसी विशेष क्षण पर होता है।

3.16 कोई पदार्थ एक तरल के माध्यम से गिरते हुए एकांतर में गति से निरीक्षण किया जाता है, जिसमें $a=g-bv$ होता है, यहां $g=$ भौतिक गुरुत्वाकर्षण है और $\mathrm{b}$ स्थिर है। बहुत समय बाद रिलीज़ होने के बाद, इसे सान्त्वना के साथ गिरते हुए देखा जाता है। स्थिर गति का मान क्या होना चाहिए?

3.17 एक गेंद छोड़ी जाती है और उसकी विस्थापना बनाम समय ग्राफ फिग। 3.4 दिखाया जाता है (विस्थापना $x$ जमीन से है और सभी मात्राएं + ऊपर की ओर हैं)।

(a) रैखिक प्रकार से वेग समय ग्राफ बनाएं।

(b) रैखिक प्रकार से त्वरण समय ग्राफ बनाएं।

वस्तुतः आपको अपने आवेदित सामग्री का हिन्दी संस्करण चाहिए। उपयोग करें:

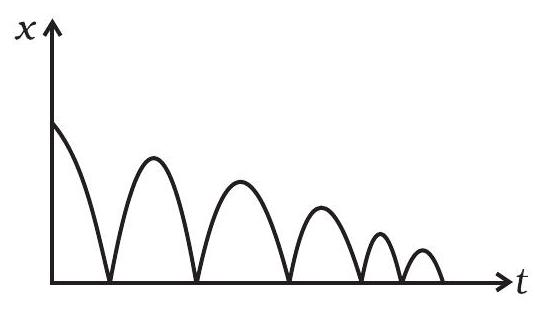
चित्र 3.4

3.18 एक कण $x(t)=x_{o}\left(1-e^{-\gamma t}\right) ; t \geq 0$ द्वारा वर्णित गति के साथ गतिशील होता है, $x_{0}>0$।

(a) कण कहां प्रारंभ होता है और किस वेग से?

(b) $x(t), v(t), a(t)$ के अधिकतम और न्यूनतम मान ढूंढें। दिखाएं कि $x(t)$ और $a(t)$ समय के साथ बढ़ते हैं और $v(t)$ समय के साथ कम होता है।

3.19 एक पक्षी एक सीधे सड़क पर एक-दूसरे की ओर चल रहे दो गाड़ियों के बीच उछल (उड़ान भर रहा) रहा है। एक गाड़ी की गति 18 $\mathrm{m} / \mathrm{h}$ है जबकि दूसरी की गति है $27 \mathrm{~km} / \mathrm{h}$। पक्षी पहली गाड़ी से दूसरी की ओर चलता है और स्पीड $36 \mathrm{~km} / \mathrm{h}$ के साथ चलता है और जब दो गाड़ियां $36 \mathrm{~km}$ दूर थीं। पक्षी द्वारा कुल कितनी दूरी तय की जाती है? पक्षी का कुल विस्थापन क्या है?

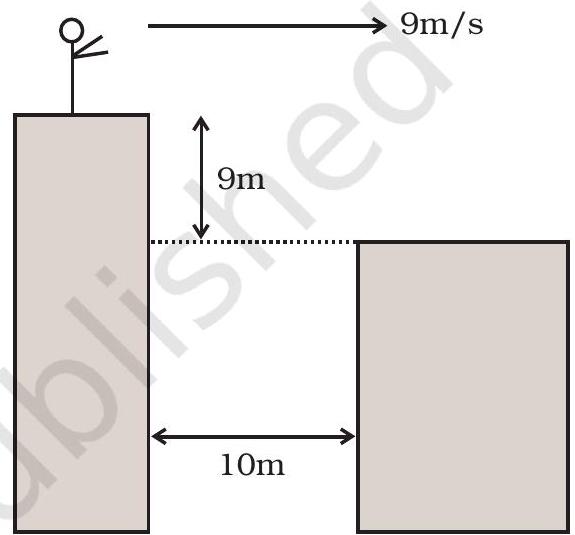
3.20 एक आदमी एक ऊँची इमारत के छत पर दौड़ता है और उम्मीद के साथ संभवत: वह अगली इमारत की छत पर लंदना चाहता है जो पहली इमारत से कम ऊँचाई पर है। यदि उसकी गति 9 $\mathrm{m} / \mathrm{s}$ है, दो इमारतों के बीच की (क्षैतिज) दूरी $10 \mathrm{~m}$ है और ऊँचाई अंतर $9 \mathrm{~m}$ है, क्या वह अगली इमारत पर लंड कर पाएगा? (यहां $g=10 \mathrm{~m} / \mathrm{s}^{2}$ लें)

3.21 एक इमारत की ऊँचाई $45 \mathrm{~m}$ है। समय-अवधि में एक और गेंद नीचे गिरायी जाती है जबकि दूसरी गेंद को औसतनी स्पीड $40 \mathrm{~m} / \mathrm{s}$ से दूसरी गेंद को ऊपर की ओर फेंका जाता है। वक्रीय गेंदों की संबंधित गति की गति के रूप में कीजिए।

3.22 एक कण की वेग-स्थानांतर ग्राफिक आई 3.5 में दिखाई गई है।

(a) $v$ और $x$ के बीच का संबंध लिखें।

(b) त्वरण और स्थानान्तर के बीच का संबंध लाएं और यह चित्रण करें।

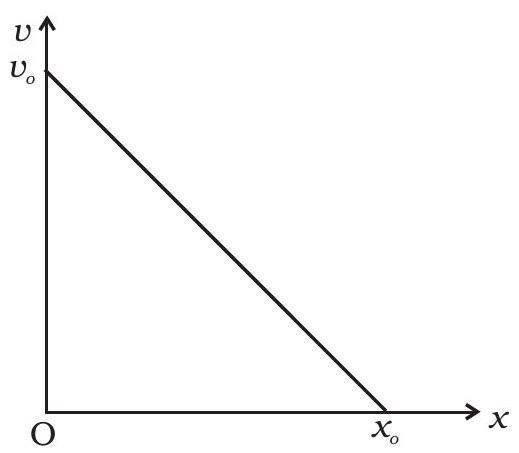
चित्र 3.5

3.23 यह सामान्य रूप से देखी जा रही है कि वर्षा के बादल भूमि से लगभग एक किलोमीटर की ऊँचाई पर हो सकते हैं।

(a) यदि एक बूंद वश में नीचे डाली जाती है तो इसकी गति क्या होगी? भी गति की गणना करें $\mathrm{km} / \mathrm{h} .\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)$ में

(b) एक आम वर्षा बूंद का व्यास लगभग $4 \mathrm{~mm}$ होता है। गति भार में होती है जब वह भूमि को छूता है।

(c) बूंद को सपाट करने के लिए आवश्यक समय का अनुमान लगाएं।

(d) पापाँच का परिवर्तन उसकी बल होता है। इस तरह की एक बूंद आप पर कितना बल दबा सकती है।

(e) छतरी पर वाणी का कोट कितना बल परिसंख्या करेगा। दो वर्षा बूंदों के बीच आम आकार 5 सेमी होता है।

(मान लें कि छतरी वृत्ताकार है और उसका व्यास $1 \mathrm{~m}$ है और कपड़ा ज़मीन को नहीं देख पड़ता है !!)

3.24 एक मोटर कार जो $72 \mathrm{~किमी / घंटा}$ की गति से चल रही है वह $3.0 \mathrm{~सेकंड}$ से कम समय में रुकने के लिए सम्भव नहीं है जबकि एक ट्रक के लिए यह समय अंतराल $5.0 \mathrm{~सेकंड}$ है। हाईवे पर कार ट्रक के पीछे हैं, दोनों $72 \mathrm{~किमी / घंटा}$ की गति से चल रही हैं। ट्रक द्वारा एक चेतावनी दी जाती है कि यह आपातकालीन में रुकने जा रहा है। कार ट्रक के साथ टकराने नहीं आनी चाहिए। मानव प्रतिक्रिया का समय $0.5 \mathrm{~सेकंड}$ है।

(टिप्पणी: यह स्पष्ट करने के लिए है कि कार्यपालित्र वाहनों को पीछे की ओर संदेश लेने की जरूरत क्यों होती है। “सुरक्षित दूरी बनाए रखें”)

3.25 एक बंदर 3 सेकंड तक एक चिकनी स्तंभ पर चढ़ता है और उसके बाद 3 सेकंड तक फिसलता है। समय $t$ पर इसकी वेग $v(t)=2 t(3-t) ; 0<t<3$ और $v(t)=-(t-3)(6-t)$, $3<t<6 \mathrm{~s}$ में होती है। यह चक्र को दोहराता है जब तक यह $20 \mathrm{~मीटर}$ ऊंचाई तक नहीं पहुँचता।

(क) बंदर की वेग कब अधिकतम होती है?

(ख) औसत वेग कब अधिकतम होता है?

(ग) मान के ऑंबर क्षेत्र में तत्वर कब अधिकतम मात्रा में होता है?

(घ) ऊचाई तक पहुंचने के लिए कितने चक्र (भिन्नों को गिनते हुए) की आवश्यकता होती हैं?

3.26 एक आदमी एक इमारत के ऊपर खड़ा है। वह दो गेंदों को लंबवत ढंकते हैं, एक $t=0$ पर और दूसरी एक समय अंतराल (2 सेकंड से कम वक्त) के बाद। दूसरी गेंद के लिए पहली गेंद की आधा वेग से फेंकी जाती है। पहली और दूसरी गेंद के बीच ईशान अंतर $t=2 \mathrm{~s}$ पर $+15 \mathrm{~m}$ होता है। यह अंतर स्थिर बना रहता है। गेंदों को फेंकने की वेग और उनके फेंकने के बीच यथार्थ समय अंतर की गणना करें।

$t=\sqrt{\frac{2\left(y-y_{o}\right)}{g}} \rightarrow \sqrt{\frac{2 \times 9 \mathrm{~m}}{10 \mathrm{~m} / \mathrm{s}^{2}}}=\sqrt{1.8} \approx 1.34$ seconds.

इस समय में, समकोणिक दूरी गतिशीलता है

$x-x_{o}=v_{o x} t=9 \mathrm{~m} / \mathrm{s} \times 1.34 \mathrm{~s}=12.06 \mathrm{~m}$.

हाँ-वह जमीन पर उतर जाएगा।

3.21 दोनों मुक्त अवस्था में हैं। इसलिए, एक के संबंध में कोई त्वरण नहीं होता है। इसलिए, सापेक्ष गति स्थिर रहती है $(=40 \mathrm{~m} / \mathrm{s})$।

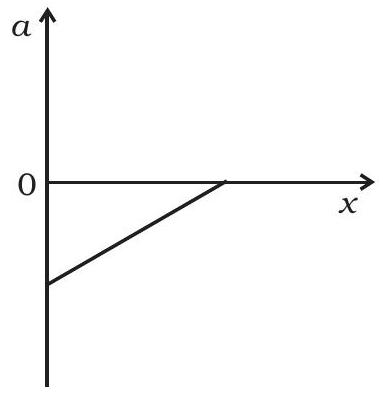
3.22 $v=\left(-v_{0} / x_{0}\right) x+v_{0}, a=\left(v_{0} / x_{0}\right)^{2} x-v_{0}^{2} / x_{0}$

वेग के साथ $a$ का परिवर्तन उस आकृति में दिखाया गया है। यह एक रेखांकन रेखा है जिसका सकारात्मक ढलान और नकारात्मक प्रतिष्ठान है।

3.23 (a) $v=\sqrt{2 g h}=\sqrt{2 \times 10 \times 1000}=141 \mathrm{~m} / \mathrm{s}=510 \mathrm{~km} / \mathrm{h}$.

(b) $\quad m=\frac{4 \pi}{3} r^{3} \rho=\frac{4 \pi}{3}\left(2 \times 10^{-3}\right)^{3}\left(10^{3}\right)=3.4 \times 10^{-5} \mathrm{~kg}$.

$$ P=m v \approx 4.7 \times 10^{-3} \mathrm{~kg} \mathrm{~m} / \mathrm{s} \approx 5 \times 10^{-3} \mathrm{~kg} \mathrm{~m} / \mathrm{s} . $$

(c) $\quad$ व्यास $\approx 4 \mathrm{~mm}$

$$ \Delta t \approx d / v=28 \mu \mathrm{s} \approx 30 \mu \mathrm{s} $$

(d) $F=\frac{\Delta P}{\Delta t}=\frac{4.7 \times 10^{-3}}{28 \times 10^{-6}} \approx 168 \mathrm{~N} \approx 1.7 \times 10^{2} \mathrm{~N}$.

(e) वक्र-अनुप्रदेशित क्षेत्र $=\pi d^{2} / 4 \approx 0.8 \mathrm{~m}^{2}$

औसत अलगाव के साथ गिरने वाली बूंदों की संख्या $\frac{0.8 \mathrm{~m}^{2}}{\left(5 \times 10^{-2}\right)^{2}} \approx 320$ होगी।

संकुचित बल $\approx 54000$ N (वातावरण द्रव्यता द्वारा बूंदों को प्रायः रोका जाता है)।

3.24 ट्रक के पीछे की कार

ट्रक की दूसरी तरफ होने के कारण $=\frac{20}{5}=4 \mathrm{~ms}^{-2}$

कार की धीरगता $=\frac{20}{3} \mathrm{~ms}^{-2}$

जब ब्रेक लगाए जाते हैं, ट्रक की दूरी को $x$ की दृष्टि से देखा जाए,

$t>0.5 \mathrm{~s}$ के लिए ट्रक का दूरी $=x+20 t-2 t^{2}$।

ए की दूरी में कार $=10+20(t-0.5)-\frac{10}{3}(t-0.5)^{2}$।

अगर ये दोनों मिलें

$x+20 t-2 t^{2}=10+20 t-10-\frac{10}{3} t^{2}+\frac{10}{3} t-0.25 \times \frac{10}{3}$।

$x=-\frac{4}{3} t^{2}+\frac{10}{3} t-\frac{5}{6}$।

$x_{\text {min }}$ निकालने के लिए,

$\frac{d x}{d t}=-\frac{8}{3} t+\frac{10}{3}=0$

इससे $t_{\min }=\frac{10}{8}=\frac{5}{4} \mathrm{~s}$ मिलता है।

इसलिए, $x_{\min }=-\frac{4}{3}\left(\frac{5}{4}\right)^{2}+\frac{10}{3} \times \frac{5}{4}-\frac{5}{6}=\frac{5}{4}$।

इसलिए, $x>1.25 \mathrm{~m}$।

द्वितीय विधि: इस विधि में तर्क यंत्र का उपयोग नहीं किया जाता है।

अगर कार ट्रक के पीछे है,

वाहन $V_{\text {car }}=20-(20 / 3)(t-0.5)$ के लिए है, $t>0.5 \mathrm{~s}$ के बाद ही वाहन धीमा होता है।

$V_{\text {truck }}=20-4 t$

इन दोनों को समान करके या वेग vs समय ग्राफ से $t$ निकाला जा सकता है। इससे $t=5 / 4 \mathrm{~s}$ मिलता है।

इस समय में ट्रक $21.875$ मीटर यात्रा करेगा और कार $23.125$ मीटर यात्रा करेगी।

इसलिए $S_{\text {car }}-S_{\text {truck }}=1.25 \mathrm{~m}$।

यदि कार शुरुआत में इस दूरी को बनाए रखती है, तो $1.25 \mathrm{~s}$ के बाद उसकी गति हमेशा ट्रक से कम होगी और इसलिए कोलिशन कभी नहीं होगा।

3.25 (अ) $(3 / 2) \mathrm{s}$, (ब) $(9 / 4) \mathrm{s}$, (सी) $0.3 \mathrm{~s}$, (डी) 6 साइकिल।

3.26 $v_{1}=20 \mathrm{~m} / \mathrm{s}, v_{2}=10 \mathrm{~m} / \mathrm{s}$, समय का अंतर $=1 \mathrm{~s}$।