अध्याय 11

विकिरण और पदार्थ का द्वैतीय स्वभाव

MCQ I

~~ 11.1 एक कण एक ऊचाई $H$ से ड्रॉप होता है। ऊचाई के रूप में कण की दे ब्रॉगली तरंगलंब अनुपातित होती है

(a) $H$

(b) $H^{1 / 2}$

(c) $H^{0}$

(b) $H^{-1 / 2}$

~~ 11.2 न्यूक्लियस से बंधे विधुत नियोसक से प्रोटॉन को हटाने के लिए फोटन की तरंगलंब लगभग होती है

(a) $1.2 nm$

(b) $1.2 \times 10^{-3} nm$

(c) $1.2 \times 10^{-6} nm$

(d) $1.2 \times 10^{1} nm$

~~ 11.3 एक खाली चैम्बर में रखे गए एक मेटल सतह पर एक इलेक्ट्रॉन के बीम (प्रत्येक इलेक्ट्रॉन के साथी $E_0$) को ध्यान में रखें। फिर (a) कोई इलेक्ट्रॉन निकाला नहीं जाएगा क्योंकि केवल फोटन निकाल सकते हैं।

(b) इलेक्ट्रॉन निकाले जा सकते हैं लेकिन सभी $E_0$ के साथ।

(c) ईकैशी ऊर्जा के साथ किसी भी ऊर्जा के साथ इलेक्ट्रॉन निकाली जा सकती है, एक अधिकतम $E_0-\phi$ (जहां $\phi$ कार्य संख्या है)।

(d) किसी भी ऊर्जा के साथ इलेक्ट्रॉन निकाली जा सकती है, एक अधिकतम के साथ $E_0$।

~~ 11.4 एनसीईआरटी कक्षा बारहवीं की भौतिकी की पाठशाला में चित्र 11.7 को विचार करें। अगर एक्स पर लगाने योग्य वोल्टेज बढ़ा दिया गया है। विकर्ण बीम का मान $\theta$ प्राथमिक मान पर होगा जो

(a) पहले के मान से अधिक होगा।

(b) पहले के मान के समान होगा।

(c) पहले के मान से कम होगा।

(d) लक्ष्य पर निर्भर करेगा।

~~ 11.5 एक प्रोटॉन, एक न्यूट्रॉन, एक इलेक्ट्रॉन और एक अल्फा-कण एक ही ऊर्जा रखते हैं। तब उनके दे ब्रॉगली तरंगलंब इस प्रकार होती है

(a) $\lambda_p=\lambda_n>\lambda_e>\lambda _{\alpha}$

(b) $\lambda _{\alpha}<\lambda_p=\lambda_n>\lambda_e$

(c) $\lambda_e<\lambda_p=\lambda_n>\lambda _{\alpha}$

(d) $\lambda_e=\lambda_p=\lambda_n=\lambda _{\alpha}$

~~ 11.6 एक इलेक्ट्रॉन एक प्राथमिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}$ के साथ गति में है और यह एक चुम्बकीय क्षेत्र $\mathbf{B}=B_0 \hat{\mathbf{j}}$ में है। तब यह दे ब्रॉगली तरंगलंब

(a) स्थिर रहती है।

(b) समय के साथ बढ़ती है।

(c) समय के साथ कम होती है।

(d) नियमित रूप से बढ़ती और कम होती है।

~~ 11.7 एक इलेक्ट्रॉन (मास $m$) एक प्राथमिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}(v_0>0)$ के साथ एक विद्युत क्षेत्र $\mathbf{E}=-E_0 \hat{\mathbf{i}}(E_0=.$ निर्धारित $.>0)$ में है। समय $t$ पर इसकी दे ब्रॉगली तरंगलंब निम्नलिखित से दी गई है

(a) $ \frac{\lambda_0}{(1+\frac{e E_0}{m} \frac{t}{v_0})} $

(b) $\lambda_0(1+\frac{e E_0 t}{m v_0})$

(c) $\lambda_0$

(d) $\lambda_0 t$.

~~ 11.8 एक इलेक्ट्रॉन (मास $m$) एक प्राथमिक वेग $\mathbf{v}=v_0 \hat{\mathbf{i}}$ के साथ एक विद्युत क्षेत्र $\mathbf{E}=E_0 \hat{\mathbf{j}}$ में है। यदि $\lambda_0=h / m v_0$ है, तो समय $t$ पर इसकी दे ब्रॉगली तरंगलंब निम्नलिखित से दी गई है

(a) $\lambda_0$

(b) $\lambda_0 \sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}$

(c) $\frac{\lambda_0}{\sqrt{1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}}}}$

(d) $\frac{\lambda_0}{(1+\frac{e^{2} E_0^{2} t^{2}}{m^{2} v_0^{2}})}$

MCQ II

~~

भाषांतर का हिंदी संस्करण क्या है:

11.9 संबंधीय सुधार प्रतिस्थापित होते हैं, जब गतिकी ऊर्जा के लिए व्यक्ति की भार $\frac{1}{2} m v^{2}$, के समानियता होती है, में $m c^{2}$ के साथ, जहां $m$ काण का भार है। एक इलेक्ट्रॉन के लिए संबंधीय सुधार कब महत्वपूर्ण होंगे ब्रोगली तड़कर दूरी पर?

(a) $\lambda=10 न्म$

(b) $\lambda=10^{-1} न्म$

(c) $\lambda=10^{-4} न्म$

(d) $\lambda=10^{-6} न्म$

~~ 11.10 दो कण $A _{1 s}$ और $A_2$ की भार $m_1, m_2(m_1>m_2)$ एक ही दह ब्रोगली तड़कर दूरी है। तो

(a) उनका चंचली है।

(b) उनकी ऊर्जाएँ समान हैं।

(c) $A_1$ की ऊर्जा $A_2$ की ऊर्जा से कम है।

(d) $A_1$ की ऊर्जा $A_2$ की ऊर्जा से अधिक है।

~~ 11.11 फोटन की दह ब्रोगली तड़कर दूरी एक इलेक्ट्रॉन की द्विगुणा है। इलेक्ट्रॉन की गति $v_e=\frac{c}{100}$ है। तो (a) $\frac{E_e}{E_p}=10^{-4}$

(b) $\frac{E_e}{E_p}=10^{-2}$

(c) $\frac{p_e}{m_e c}=10^{-2}$

(d) $\frac{p_e}{m_e c}=10^{-4}$.

~~ 11.12 पदार्थ में विर्ट संघटित फोटोन गर्मी में परिवर्तित होते हैं। $1 kg$ भार वाली ठंडी $0^{\circ} C$ में पानी में रूपांतरण के लिए $n$ फोटन/सेक से निर्मित करने के लिए एक स्रोत का उपयोग किया जाता है, जिसकी तदद गणना $v$ है। तो, परिवर्तन के लिए लिया जाने वाला समय $T$

(a) स्थिर $n$, $v$ बदल रहे हों और $n v=$ सबसंभवता.

(b) $n$ स्थिर, $v$ बढ़ती हुई

(c) $n v=$ साबित रखने के साथ $n$ और $v$ बदलने पर स्थिर रहता है।

(d) जब उत्पाद $n v$ बदलेगा तो बढ़ता है।

~~ 11.13 एक कण मूलवत एक संकुचित परिधि में चलता है, जो संकुचित स्थान की ओर दिशा से एक बाधात्मक बल के कारण यात्रा करता है। ब्रोगली तड़कर बाधात्मक बाढ़ने बाधात्मकस्थिति के बीच में विव:कस्थिति $\lambda_1$, $\lambda_2$ के साथ चक्रीय रूप में बदलती है। निम्नलिखित कथनों में से कौन से सत्य हैं?

(a) कण मूलवत संकुचित स्थान की ओर चक्रीय यात्रा कर सकता है

(b) कण मूलवत में एक न्यूनाधिकी ब्रोगली तड़कर दूरी के साथ एक अलमारिक यात्रा कर सकता है।

(c) जब ब्रोगली तन्त्र की लंबाई $\lambda_1$ होती है, तो कण $\lambda_2$ के मान से अधिक ऊर्जा से मूलवत की ओर होता है।

(d) जब ब्रोगिलिक तन्त्र $\lambda_2$ होती है, तो कण $\lambda_1$ के मान से अधिक ऊर्जा से मूलवत की ओर होता है।

वीएसए

~~ 11.14 एक प्रोटॉन और एक $\alpha$-कण के बीच योगदानी भीतरी होती है, एक ही पोटेशियल अंतर का प्रयोग करके। कैसे एक दह ब्रोगली तड़कर दूरी $\lambda_p$ और $\lambda_a$ एक दूसरे संबंधित होती हैं?

~~ 11.15 (i) प्रोजेक्टर के प्रकाश के विवरण में, हम शुन्यांक पर एक फोटॉन का ध्यान देते हैं जो इलेक्ट्रॉन के साथ टकराता है और अपनी ऊर्जा स्थानांतरित करता है। इससे निक्षेप की गई इलेक्ट्रॉन के लिए अधिकतम ऊर्जा $E _{\max }$ के लिए समीकरण बनाता है

$ E _{\max }=h v-\phi_0 $

जहां $\phi_0$ मेटल का काम कार्य है। अगर इलेक्ट्रॉन 2 (हर एक $v$वाला) फोटॉन पा मर्गदर्शन करे तो निक्षेप की गई इलेक्ट्रॉन के लिए अधिकतम ऊर्जा क्या होगी?

(ii) हमारे स्थिर की चर्चा में इस तथ्य (द्विफोटॉन अवशेषन) को क्यूँ नहीं लेते?

~~

11.16 ऐसे सामग्री हो सकती हैं जो छोटे तरंगदैर्घ्य के फोटनों को अवशोषित करती हैं और बड़े तरंगदैर्घ्य के फोटनों को कमजोर करती हैं। क्या स्थिर पदार्थ हो सकते हैं जो बड़े तरंगदैर्घ्य के फोटनों को अवशोषित करते हैं और छोटे तरंगदैर्घ्य के प्रकाश को उत्पन्न करते हैं।

~~ 11.17 क्या सभी इलेक्ट्रॉन जो फोटन अवशोषित करते हैं वे फोटोइलेक्ट्रॉन के रूप में निकलते हैं?

~~ 11.18 दो प्रकाश स्रोत हैं, प्रत्येक $100 वाट$ की शक्ति के साथ प्रकाशित करते हैं। एक $1 नैनोमीटर$ तरंगदैर्घ्य पर एक्स-रे को निकालता है और दूसरा $500 नैनोमीटर$ पर दिखाई देने वाला प्रकाश। निर्दिष्ट तरंगदैर्घ्य के एक्स-रे के फोटनों की संख्या का अनुपात दिखाई दें?

SA

~~ 11.19 फोटोइमिशन के लिए आलेख 11.1 को विचार करें।

मॉमेंटम-संरक्षण के साथ शानदार कैसे मिलाएंगे? ध्यान दें कि प्रकाश (फोटन) उत्पन्न इलेक्ट्रॉनों के प्रकाश से एक अलग दिशा में मॉमेंटम होता है।

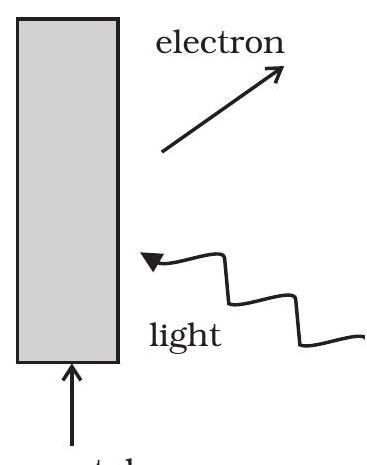आलेख 11.1

~~ 11.20 $600 नैनोमीटर$ के प्रकाश के सामने एक धातु पर विचार करें। प्रकाश के $400 सैन्योमीटर$ के तरंगदैर्घ्य का उपयोग करने पर इलेक्ट्रॉन की अधिकतम ऊर्जा दोगुनी होती है। ईवी में कर्म निर्धारित करें।

~~ 11.21 एक इलेक्ट्रॉन को $1 नैनोमीटर$ चौड़े क्षेत्र में सीमित मानें, हाइज़ेनबर्ग अनिश्चितता सिद्धांत (एनसीईआरटी की पाठ्यपुस्तक के द्वारा भूतकाल किए गए Eq 11.12) का उपयोग करके, तत्वबिंदु के अनिश्चितता $\Delta x$ के रूप में मानें। स्थिति $\Delta p$ के रूप में मानते हुए, ईवी में इलेक्ट्रॉन की ऊर्जा निर्धारित करें।

~~ 11.22 बीम ए और बीम बी दो मनोक्रोमेटिक बालों की बराबर प्रकाश प्रवाहित है। बीम ए के द्वारा स्क्रीन को हिट करने वाले फोटनों की संख्या बीम बी की दोगुनी है। इनकी आवृत्तियों के बारे में आप कौन सी साक्ष्य कर सकते हैं?

~~ 11.23 दो टुकड़ों ए और बी का दे Broglie तरंगदैर्घ्य $\lambda_1$ और $\lambda_2$ है। एक तत्व $सी$ बनाने के लिए प्रक्रिया प्रकाशरूप समान्वय करती है। चाल संरक्षण को करने वाली प्रकाशिका की De Broglie तरंगदैर्घ्य निर्धारित करें। (गतिविधि एकबारगामी है)।

~~ 11.24 $E=0.1 nm$ धातु के सतह पर ऊर्जा $E$ न्यूट्रॉन बीम द्वारा परावर्तन की गई है। परावर्तित बीम में पहली अधिकतम तीव्रता $30^{\circ}$ पर होती है। बीम की किनेटिक ऊर्जा $E$ क्या है? ($अयोग्य। $)

LA

~~ 11.25 एक पतला लक्ष्य ले $(10^{-2} m$ का वर्ग, $10^{-3} m$ मोटाई) जिस पर सोडियम की फोटोचाल बनाता है, जब उस पर $100 W / m ^ {2} (\lambda = 660 nm)$ की तेजी से प्रकाश पड़ती है। जब कोई फोटॉन सोडियम पर टक्कर मारता है, तो फोटोइलेक्ट्रॉन उत्पन्न होने की संभावना क्या है? [$Na$ की घनत्वा $= 0.97 kg / m^{3}$ स्वीकार करें]।

~~ 11.26 एक इलेक्ट्रॉन $द$ से एक धातुरेखा के सामकोणी पटले के सामने होता है (जिसे अकेली रेखा सत्त्व माना जाता है)। मानिये प्लेट द्वारा आकर्षण की बल प्रदान की जाती है जैसे $\frac{1}{4} \frac{q^{2}}{4 \pi \varepsilon_0 d^{2}}$

प्लेट से असीमित दूरी पर चार्ज ले जाने में काम कीजिए। $d=0.1 nm$ लेते हुए, इलेक्ट्रॉन वोल्ट्स में काम किया जाता है। [ऐसी कोई बाल विधि $d<0.1 nm$ के लिए सही नहीं होती है]।

11.27 एक छात्र दो माल माल C और D का प्रयोग फोटोइलेक्ट्रिक प्रभाव पर करता है। संख्यात्मकरण jvjx ojokyk v s v d dqf”V _{\text{stop }} v s””v” bggrs Fig. 11.2।

(i) C कार्य चालकता है या $D$?

(ii) एक इलेक्ट्रॉन के विद्युत आवेश की फ़ीमे $=1.6 \times 10^{-19} C$, प्रयोग से पायी गयी $h$ की मान्यता को ढूंढें एवं C और $D$ दोनों के लिए उसी से मान्यता कर :।

यह यथार्थी इस्टीन के सिद्धांत से संगम होता है इस बारे में टिप्पणी करें:।

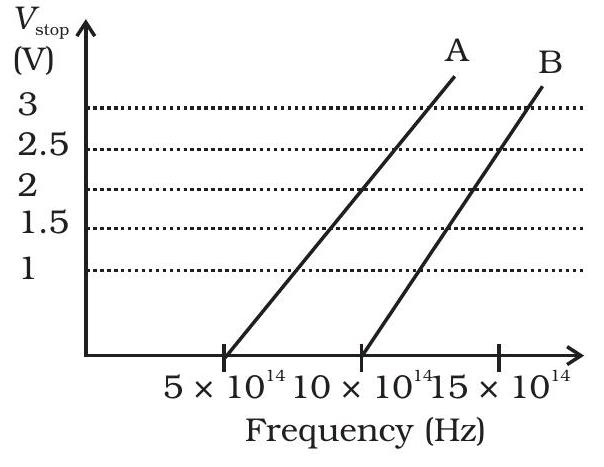Fig. 11.2

~~ 11.28 एक अणु A जिसका वजन $m_A$ है, एक गति $v$ और शांतित अवस्था में अणु B ($m_B$) से टकराती है(एक आयामी आरम्भना)। चाल की प्रवृति को निरेखित करें dustp inka JK,h` auksthaast maank jk"ma_A".a nuksw jaanmark ga ihV raV kiirt? टुकरान होगा?

~~ 11.29 एक $20 W$ विकिवाली बल्ब $5000 \AA$ वेवलैंथ की रोशनी को ऐकथ्य करता हैं और इसे $2 m$ दूरी पर रखे हुए धातु सतह पर पठाता हैं। मान लीजिये कि धातु सतह का कार्य चालकता $2 eV$ हैं और धातु सतह का प्रत्येक परमणु एक $1.5 A$ वक्र हैं।

(i) बल्ब द्वारा प्रति सेकंड प्रकाशित फोटॉनों की संख्या अनुमान लगाइए। [कोई अन्य हानि मानने।]

(ii) क्या फोटोइलेक्ट्रिक उद्धरण होगा?

(iii) कितना समय आविक व्यास ( $2 eV$ ) के समान ऊर्जा पर पहुँचने के लिए परमणु वक्र को चाहिएगा?

(iv) (iii) के ऊपर गणना किए गए समय अवधि में बर्कियम वक्र को कितने फोटॉन प्राप्त होंगे?

(v) क्या आप व्याख्या कर सकते हैं कि कैसे फोटोइलेक्ट्रिक प्रभाव तुरंत देखा गया था?

संकेत: भाग (iii) में गणना आधारिक लोकवादी है और आप आगे धातु सतह के लक्षित का क्षेत्र उदहारण कहें सकते हैं $1 cm^{2}$ और अनुमान लगाने के लिए कि क्या होगा?

अध्याय 11

~~ 11.1 (डी)

~~ 11.2 (बी)

~~ 11.3 (डी)

~~ 11.4 (सी)

~~ 11.5 (बी)

~~ 11.6 (ए)

~~ 11.7 (ए)

~~ 11.8 (सी)

~~ 11.9 (सी), (डी)

~~ 11.10 (ए), (सी)

~~ 11.11 (बी), (सी)

~~ 11.12 (ए), (बी), (सी)

~~ 11.13 (बी), (डी)

~~ 11.14 $ \quad \lambda_p / \lambda_d=p_x / p_p=\frac{\sqrt{2 m _{\alpha} E _{\alpha}}}{\sqrt{2 m_p E_p}}=\sqrt{8}: 1$

~~ 11.15 (i) $E _{\max }=2 h v-\phi$

(ii) नियमित तरह से 2 फोटॉनों द्वारा इलेक्ट्रॉन द्वारा विलंबित होने की संभावना बहुत कम हैं। इसलिए ऐसे उत्सर्जन को तुच्छ माना जायेगा।

~~ 11.16 पहले मामले में, दियी गयी ऊर्जा प्राप्त ऊर्जा से कम होती है। दूसरी मामले में, वस्त्र को ऊर्जा प्रदान करनी होगी, क्योंकि उत्सर्जित फोटॉन की ऊर्जा अधिक होती है। यह स्थिर पदार्थों के लिए संभव नहीं हो सकता।

~~ 11.17 नहीं, धातु के अधिकांश इलेक्ट्रॉन मेल द्वारा बहाए गए होते हैं। केवल कुछ ही मेटल के सतह से बाहर आते हैं।

~~ 11.18 कुल $E$ स्थिर है

$X$-रेखा और द्रश्यमान इलाके वाले फोटॉनों की संख्या के मध्यांतर निम्नलिखित समानता करें:

$n_1 E_1=n_2 E_2$

$n_1 \frac{h c}{\lambda_1}=n_2 \frac{h c}{\lambda_2}$

$\frac{n_1}{n_2}=\frac{\lambda_1}{\lambda_2}$

$\frac{n_1}{n_2}=\frac{1}{500}$.

~~

11.19 धारणा ध्रुवक और इलेक्ट्रॉनिक्स को संसोधित किए जाने के लिए परमाणु स्तर पर एटम फोटन को अवशोषित करते हैं। उत्सर्जित इलेक्ट्रॉन को उत्कटता के साथ छोड़ दिया जाता है। धारणा संरक्षण में तत्व को और इलेक्ट्रॉनिक्स को संसर्गित गति को लेना होता है।

~~ 11.20 अधिकतम ऊर्जा $= h v-\phi$

$(\frac{1230}{600}-\phi)=\frac{1}{2}(\frac{1230}{400}-\phi)$

$\phi=\frac{1230}{1200}=1.02 eV$.

~~ 11.21 $ \Delta x \Delta p \simeq \hbar$

$\Delta p \simeq \frac{\hbar}{\Delta x} \simeq \frac{1.05 \times 10^{-34} Js}{10^{-9} m}=1.05 \times 10^{-25}$

$E=\frac{p^{2}}{2 m}=\frac{(1.05 \times 10^{-25})^{2}}{2 \times 9.1 \times 10^{-31}}=\frac{1.05^{2}}{18.2} \times 10^{-19} J=\frac{1.05^{2}}{18.2 \times 1.6} eV$

$=3.8 \times 10^{-2} eV$

~~ 11.22 $ I=n_A n_A=n_B v_B$

$\frac{n_A}{n_B}=2=\frac{v_B}{v_A}$

$B$ तरंग का आवृत्ति $A$ तरंग की दोगुनी है।

~~ 11.23

$p_c=|p_A|+|p_B|=\frac{h}{\lambda_A}+\frac{h}{\lambda_B}=\frac{h}{\lambda_c}=\frac{h}{\lambda_c}$ if $p_A, p_B>0$ or $p_A, p_B<0$

या $\lambda_c=\frac{\lambda_A \lambda_B}{\lambda_A+\lambda_B}$

अगर $p_A>0, p_B<0$ या $p_A<0, p_B>0$ होता है

$p_c=h \frac{\lambda_B-\lambda_A}{|\lambda_A \cdot \lambda_B|}=\frac{h}{\lambda_c}$

$\lambda_c=\frac{\lambda_B \cdot \lambda_A}{|\lambda_A-\lambda_B|}$.

~~ 11.24 $2 d \sin \theta=\lambda=d=10^{-10} m$.

$ \begin{gathered} p=\frac{h}{10^{-10}}=\frac{6.6 \times 10^{-34}}{10^{-10}}=6.6 \times 10^{-21} kg m / s \\ E=\frac{(6.6 \times 10^{-24})^{2}}{2 \times(1.7 \times 10^{-27})} \times 1.6 \times 10^{-19}=\frac{6.6^{2}}{2 \times 1.7} \times 1.6 \times 10^{-2} eV \\ =20.5 \times 10^{-2} eV=0.21 eV \end{gathered} $

~~ 11.25 $6 \times 10^{26} नाय्ट्रियम एटम $ का वजन $23 kg$ है।

टारगेट का आयतन $=(10^{-4} \times 10^{-3})=10^{-7} m^{3}$

नाय्ट्रियम का घनत्व $=(d)=0.97 kg / m^{3}$

$6 \times 10^{26} नाय्ट्रियम एटम$ का आयतन $=\frac{23}{0.97} m^{3}=23.7 m^{3}$

एक नाय्ट्रियम एटम के आयतन $=\frac{23}{0.97 \times 6 \times 10^{26}} m^{3}=3.95 \times 10^{-26} m^{3}$

टारगेट में नाय्ट्रियम एटमों की संख्या $=\frac{10^{-7}}{3.95 \times 10^{-26}}=2.53 \times 10^{18}$

$10^{-4} m^{2}$ के लिए बीम में फोटनों की संख्या प्रति सेकंड $n$

प्रति सेकंड ऊर्जा $n h v=10^{-4} J \times 100=10^{-2} W$

$h v($ लिए $\lambda=660 nm)=\frac{1234.5}{600}$

$ =2.05 eV=2.05 \times 1.6 \times 10^{-19}=3.28 \times 10^{-19} J $

$n=\frac{10^{-2}}{3.28 \times 10^{-19}}=3.05 \times 10^{16} / s$

$n=\frac{1}{3.2} \times 10^{17}=3.1 \times 10^{16}$

यदि $P$ प्रति एटम, प्रति फोटन निकासी की संभावना है, तो प्रति सेकंड निकलने वाले फोटोइलेक्ट्रों की संख्या

$=P \times 3.1 \times 10^{16} \times 2.53 \times 10^{18}$

विद्युत धारा $=P \times 3.1 \times 10^{+16} \times 2.53 \times 10^{18} \times 1.6 \times 10^{-19} A$

$ =P \times 1.25 \times 10^{+16} A $

यह $100 \mu A$ के बराबर होना चाहिए या

$P=\frac{100 \times 10^{-6}}{1.25 \times 10^{+16}}$

$\therefore P=8 \times 10^{-21}$

इस प्रकार, एक एकल फोटन द्वारा एक एकल परमाणु पर प्रकाशविस्फोटन की संभावना बहुत कम होती है जो 1 से बहुत कम होती है। (इसीलिए एक परमाणु द्वारा दो फोटनों के शोषण को अल्प ही माना जाता है)।

~~ ११.२६ एक बाह्य एजेंसी द्वारा किया गया कार्य $=+\frac{1}{4 \pi \varepsilon_0} \cdot \frac{1}{4} \int_d^{\infty} \frac{q^{2}}{x^{2}} d x=\frac{1}{4} \cdot \frac{q^{2}}{4 \pi \varepsilon_0 d}$

$d=0.1 \text{ नॅनोमीटर}$ के साथ ऊर्जा $=\frac{(1.6 \times 10^{-19}) \times 9 \times 10^{9}}{4(10^{-10}) \times 1.6 \times 10^{-19}} eV$

$ =\frac{1.6 \times 9}{4} eV=3.6 eV $

~~ ११.२७ (i) बी के लिए एक अधिक चरम आवृत्ति पर रुकती तनाव $=0$। इसलिए इसका एक अधिकतम कार्यान्वयन है।

(ii) A के लिए ढाल $=\frac{h}{e}=\frac{2}{(10-5) \times 10^{14}}$।

$ =\frac{2.5}{(15-10) \times 10^{14}} \text{ बी के लिए} $

$ \begin{aligned} h= & \frac{1.6 \times 10^{-19}}{5} \times 2 \times 10^{-14}=6.04 \times 10^{-34} \text{ जूल-सेकंड A के लिए} \\ & =\frac{1.6 \times 10^{-19} \times 2.5 \times 10^{-14}}{5}=8 \times 10^{-34} \text{ जूल-सेकंड B के लिए} . \end{aligned} $

क्योंकि $h$ अलग-अलग है, इसलिए प्रयोग सिद्धांत के साथ संरूप नहीं है।

~~ ११.२८

$म_A व=म_A व_1+म_B व_2$

$\frac{1}{2} म_A व^{2}=\frac{1}{2} म_A व_1^{2}+\frac{1}{2} म_B व_2^{2}$

$\therefore \frac{1}{2} म_A(व-व_1)(v_A+v_1)=\frac{1}{2} म_B v_B^{2}$

$\therefore व+व_1=व_2$

या $व=व_2-व_1$

$\therefore व_1=(\frac{म_A-म_B}{म_A+म_B}) व, \quad$ और $\quad व_2=(\frac{2 म_A}{म_A+म_B}) व$

$\therefore \lambda _{\text{प्रारंभिक }}=\frac{h}{म_A व}$

$\lambda _{\text{अंतिम }}=\frac{h}{म_A व}=|\frac{h(म_A+म_B)}{म_A(म_A-म_B) व}|$

$\therefore \Delta \lambda=\frac{h}{म_A व}[|\frac{.म_A+म_B)}{म_A-म_B}|-1]$

~~ ११.२९ (i) $\frac{d N}{d t}=\frac{P}{(h c / \lambda)}=5 \times 10^{19} / s$

(ii) $\frac{h c}{\lambda}=2.49 eV>W_0:$ हाँ।

(iii) P. $\frac{\pi r^{2}}{4 \pi d^{2}} \Delta t=W_0, \Delta t=28.4 s$

(iv) $N=(\frac{d N}{d t}) \times \frac{\pi r^{2}}{4 \pi d^{2}} \times \Delta t=2$