Thermodynamics and Thermochemistry - Result Question 45
45. For an ideal gas, consider only $P-V$ work in going from initial state $X$ to the final state $Z$. The final state $Z$ can be reached by either of the two paths shown in the figure.
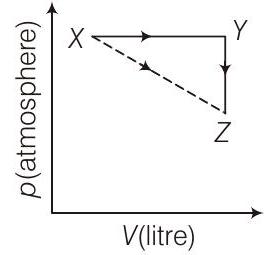
[Take $\Delta S$ as change in entropy and $W$ as work done].
Which of the following choice(s) is (are) correct? (2012)
(a) $\Delta S _{X \rightarrow Z}=\Delta S _{X \rightarrow Y}+\Delta S _{Y \rightarrow Z}$
(b) $W _{X \rightarrow Z}=W _{X \rightarrow Y}+W _{Y \rightarrow Z}$
(c) $W _{X \rightarrow Y \rightarrow Z}=W _{X \rightarrow Y}$
(d) $\Delta S _{X \rightarrow Y \rightarrow Z}=\Delta S _{X \rightarrow Y}$
Show Answer
Answer:
Correct Answer: 45. (a, c)
Solution:
(a) Entropy is a state function, change in entropy in a cyclic process is zero.
$\text { Therefore, } \quad \Delta S _{X \rightarrow Y}+\Delta S _{Y \rightarrow Z}+\Delta S _{Z \rightarrow X}=0 $
$\Rightarrow \quad-\Delta S _{Z \rightarrow X}=\Delta S _{X \rightarrow Y}+\Delta S _{Y \rightarrow Z} $
$=\Delta S _{X \rightarrow Z}$
Analysis of options (b) and (c)
Work is a non-stable function, it does depends on the path followed. $W _{Y \rightarrow Z}=0$ as $\Delta V=0$.
Therefore, $W _{X \rightarrow Y \rightarrow Z}=W _{X \rightarrow Y}$. Also, work is the area under the curve on $p-V$ diagram.
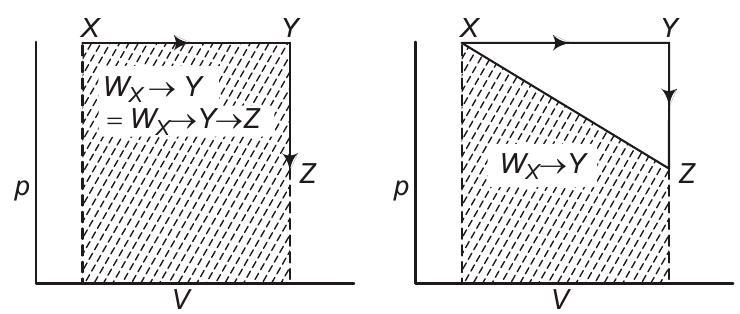
As shown above $W _{X \rightarrow Y}+W _{Y \rightarrow Z}=W _{X \rightarrow Y}=W _{X \rightarrow Y \rightarrow Z}$ but not equal to $W _{X \rightarrow Z}$.





