Area Ques 18
Question
- The area (in sq units) in the first quadrant bounded by the parabola, $y=x^{2}+1$, the tangent to it at the point $(2,5)$ and the coordinate axes is
(2019 Main, 11 Jan II)
(a) $\frac{14}{3}$
(b) $\frac{187}{24}$
(c) $\frac{8}{3}$
(d) $\frac{37}{24}$
Show Answer
Answer:
Correct Answer: 18.(d)
Solution:
Formula:
- Given, equation of parabola is $y=x^{2}+1$, which can be written as $x^{2}=(y-1)$. Clearly, vertex of parabola is $(0,1)$ and it will open upward.
Now, equation of tangent at $(2,5)$ is $\frac{y+5}{2}=2 x+1$
$\left[\because\right.$ Equation of the tangent at $\left(x _{1}, y _{1}\right)$ is given by $T=0$. Here, $\left.\frac{1}{2}\left(y+y _{1}\right)=x x _{1}+1\right]$
$y=4 x-3$
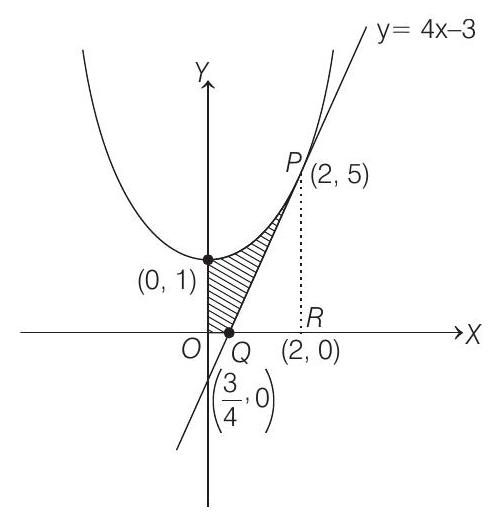
Required area $=$ Area of shaded region
$ \begin{aligned} & =\int _{0}^{2} y(\text { parabola }) d x-(\text { Area of } \triangle P Q R) \\ & =\int _{0}^{2}\left(x^{2}+1\right) d x-(\text { Area of } \triangle P Q R) \\ & =(\frac{x^{3}}{3}+x) _{0}^2 \quad-\frac{1}{2} (2-\frac{3}{4} )\cdot 5 \end{aligned} $
$\left[\because\right.$ Area of a triangle $=\frac{1}{2} \times$ base $\times$ height $]$
$ \begin{aligned} & =(\frac{8}{3}+2)-0-\frac{1}{2} (\frac{5}{4}) 5 \\ & =\frac{14}{3}-\frac{25}{8}=\frac{112-75}{24}=\frac{37}{24} \end{aligned} $





