Area Ques 19
Question
- The area (in sq units) of the region bounded by the curve $x^{2}=4 y$ and the straight line $x=4 y-2$ is
(a) $\frac{7}{8}$
(b) $\frac{9}{8}$
(c) $\frac{5}{4}$
(d) $\frac{3}{4}$
Show Answer
Answer:
Correct Answer: 19.(b)
Solution:
Formula:
- Given equation of curve is $x^{2}=4 y$, which represent a parabola with vertex $(0,0)$ and it open upward.
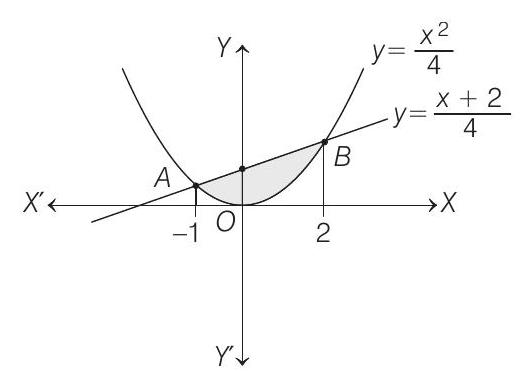
Now, let us find the points of intersection of $x^{2}=4 y$ and $4 y=x+2$
For this consider, $x^{2}=x+2$
$ \begin{array}{lr} \Rightarrow & x^{2}-x-2=0 \\ \Rightarrow & (x-2)(x+1)=0 \\ \Rightarrow & x=-1, x=2 \end{array} $
When $x=-1$, then $y=\frac{1}{4}$
and when $x=2$, then $y=1$
Thus, the points of intersection are $A(-1, \frac{1}{4})$ and $B(2,1)$.
Now, required area $=$ area of shaded region
$ \begin{aligned} & =\int _{-1}^{2}\{y \text { (line) }-y \text { (parabola) }\} d x \\ & =\int _{-1}^{2} (\frac{x+2}{4}-\frac{x^{2}}{4}) d x=\frac{1}{4} (\frac{x^{2}}{2}+2 x-{\frac{x^{3}}{3}}) _{-1}^{2} \\ & =\frac{1}{4} [(2+4-\frac{8}{3})-(\frac{1}{2}-2+\frac{1}{3})] \\ & =\frac{1}{4} (8-\frac{1}{2}-3)=\frac{1}{4} (5-\frac{1}{2})=\frac{9}{8} \text { sq units. } \end{aligned} $





