Area Ques 20
Question
- The area of the region $\mathrm{A}=\{(x, y) ; 0 \leq y \leq x|x|+1$ and $-1 \leq x \leq 1\}$ in sq. units, is
(2019 Main, 9 Jan II)
(a) $2$
(b) $\frac{4}{3}$
(c) $\frac{1}{3}$
(d) $\frac{2}{3}$
Show Answer
Answer:
Correct Answer: 20.(a)
Solution:
Formula:
- We have,
$A=\{(x, y): 0 \leq y \leq x|x|+1$ and $-1 \leq x \leq 1\}$
When $x \geq 0$, then $0 \leq y \leq x^{2}+1$
and when $x<0$, then $0 \leq y \leq-x^{2}+1$
Now, the required region is the shaded region.
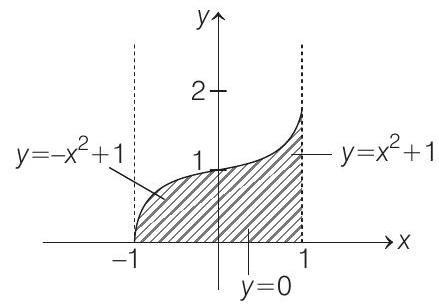
$\left[\because y=x^{2}+1 \Rightarrow x^{2}=(y-1)\right.$, parabola with vertex $(0,1)$ and $y=-x^{2}+1 \Rightarrow x^{2}=-(y-1)$,
parabola with vertex $(0,1)$ but open downward]
We need to calculate the shaded area, which is equal to
$ \begin{aligned} \int _{-1}^{0}\left(-x^{2}+1\right) & d x+\int _{0}^{1}\left(x^{2}+1\right) d x \\ & =[-\frac{x^{3}}{3}+x] _{-1}^{0}+[\frac{x^{3}}{3}+x] _{0}^{1} \\ & =(0-[-\frac{(-1)^{3}}{3}+(-1)])+([\frac{1}{3}+1]-0) \\ & =(-\frac{1}{3}-1)+\frac{4}{3} \\ & =\frac{2}{3}+\frac{4}{3}=2 \end{aligned} $





