Area Ques 26
Question
- The area (in sq units) of the region described by $A=\left\{(x, y): x^{2}+y^{2} \leq 1\right.$ and $\left.y^{2} \leq 1-x\right\}$ is
(2014 Main)
(a) $\frac{\pi}{2}+\frac{4}{3}$
(b) $\frac{\pi}{2}-\frac{4}{3}$
(c) $\frac{\pi}{2}-\frac{2}{3}$
(d) $\frac{\pi}{2}+\frac{2}{3}$
Show Answer
Answer:
Correct Answer: 26.(a)
Solution:
Formula:
- Given, $A=\left\{(x, y): x^{2}+y^{2} \leq 1\right.$ and $\left.y^{2} \leq 1-x\right\}$
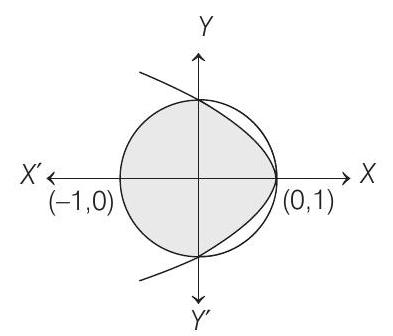
Required area $=\frac{1}{2} \pi r^{2}+2 \int _{0}^{1}\left(1-y^{2}\right) d y$
$ \begin{aligned} & =\frac{1}{2} \pi(1)^{2}+2 \quad (y-{\frac{y^{3}}{3}}) _{0}^{1} \\ & =(\frac{\pi}{2}+\frac{4}{3}) \text { sq units } \end{aligned} $





