Area Ques 27
Question
- The area enclosed by the curves $y=\sin x+\cos x$ and $y=|\cos x-\sin x|$ over the interval $[0, \frac{\pi}{2}]$ is (2014 Adv.)
(a) $4(\sqrt{2}-1)$
(c) $2(\sqrt{2}+1)$
(b) $2 \sqrt{2}(\sqrt{2}-1)$
(d) $2 \sqrt{2}(\sqrt{2}+1)$
Show Answer
Answer:
Correct Answer: 27.(b)
Solution:
Formula:
- PLAN To find the bounded area between $y=f(x)$ and $y=g(x)$ between $x=$ a to $x=b$.
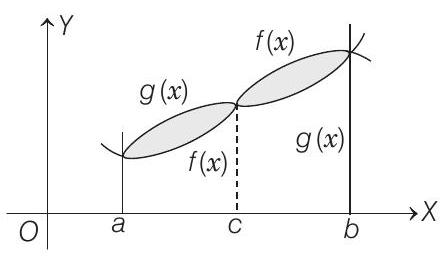
$\therefore \quad$ Area bounded $=\int _{a}^{\varepsilon}[g(x)-f(x)] d x+\int _{a}^{b}[f(x)-g(x)] d x$
$ =\int _{a}^{b}|f(x)-g(x)| d x $
Here,
$ f(x)=y=\sin x+\cos x, \text { when } 0 \leq x \leq \frac{\pi}{2} $
and
$ g(x)=y=|\cos x-\sin x| $
$ =\begin{array}{ll} \cos x-\sin x, & 0 \leq x \leq \frac{\pi}{4} \\ \sin x-\cos x, & \frac{\pi}{4} \leq x \leq \frac{\pi}{2} \end{array} $
could be shown as
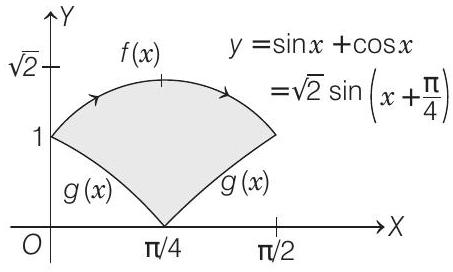
$\therefore$ Area bounded $=\int _{0}^{\pi / 4}\{(\sin x+\cos x)-(\cos x-\sin x)\} d x$
$+\int _{\pi / 4}^{\pi / 2}\{(\sin x+\cos x)-(\sin x-\cos x)\} d x$
$=\int _{0}^{\pi / 4} 2 \sin x d x+\int _{\pi / 4}^{\pi / 2} 2 \cos x d x$
$=-2[\cos x] _{0}^{\pi / 4}+2[\sin x \cdot n] _{\pi / 4}^{\pi / 2}$
$=4-2 \sqrt{2}=2 \sqrt{2}(\sqrt{2}-1)$ sq units





