Area Ques 28
Question
- If the area (in sq units) of the region $\left\{(x, y): y^{2} \leq 4 x, x+y \leq 1, \quad x \geq 0, y \geq 0\right\}$ is $a \sqrt{2}+b$, then $a-b$ is equal to
(2019 Main, 12 April)
(a) $\frac{10}{3}$
$6$
(c) $\frac{8}{3}$
(d) $-\frac{2}{3}$
Show Answer
Answer:
Correct Answer: 28.(b)
Solution:
Formula:
- Given region is $\left\{(x, y): y^{2} \leq 4 x, x+y \leq 1, x \geq 0, y \geq 0\right\}$
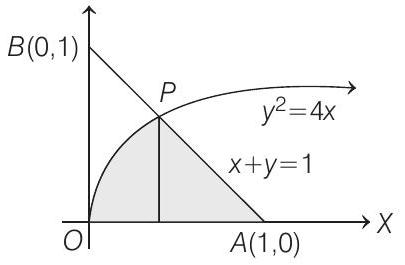
Now, for point $P$, substitute the value of $y=1-x$ into $y^{2}=4 x$, we get
$(1-x)^{2}=4 x \Rightarrow x^{2}-2 x+1=4 x$
$ \begin{aligned} \Rightarrow \quad & x^{2}-6 x+1=0 \\ \Rightarrow \quad x & =\frac{6 \pm \sqrt{36-4}}{2} \\ & =3 \pm 2 \sqrt{2} . \end{aligned} $
Since the $x$-coordinate of $P$ is less than the $x$-coordinate of point $A(1,0)$.
$\therefore \quad x=3-2 \sqrt{2}$
Now, required area.
$=\int _{0}^{3-2 \sqrt{2}} 2 \sqrt{x} d x+\int _{3-2 \sqrt{2}}^{1}(1-x) d x$
$=2|\frac{x^{3 / 2}}{3 / 2}| _{0}^{3-2 \sqrt{2}}$ $+|x-{\frac{x^{2}}{2}}| _{3-2 \sqrt{2}}^1$
$=\frac{4}{3}(3-2 \sqrt{2})^{32}+(1-\frac{1}{2})-(3-2 \sqrt{2})+\frac{(3-2 \sqrt{2})^{2}}{2}$
$=\frac{4}{3}\left[(\sqrt{2}-1)^{2}\right]^{3 / 2}+\frac{1}{2}-3+2 \sqrt{2}+\frac{1}{2}(9+8-12 \sqrt{2})$
$=\frac{4}{3}(\sqrt{2}-1)^{3}-\frac{5}{2}+2 \sqrt{2}+\frac{17}{2}-6 \sqrt{2}$
$=\frac{4}{3}(2 \sqrt{2}-3(2)+3(\sqrt{2})-1)-4 \sqrt{2}+6$
$=\frac{4}{3}(5 \sqrt{2}-7)-4 \sqrt{2}+6=\frac{8 \sqrt{2}}{3}-\frac{10}{3}$
$=a \sqrt{2}+b \quad$ (given)
So, on comparing $a=\frac{8}{3}$ and $b=-\frac{10}{3}$
$\therefore \quad a-b=\frac{8}{3}-\frac{10}{3}=-\frac{2}{3}$





