Area Ques 32
Question
- The area of the region between the curves $y=\sqrt{\frac{1+\sin x}{\cos x}}$ and $y=\sqrt{\frac{1-\sin x}{\cos x}}$ and bounded by the lines $x=0$ and $x=\frac{\pi}{4}$ is
(a) $\int _{0}^{\sqrt{2}-1} \frac{t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}} d t$
(b) $\int _{0}^{\sqrt{2}-1} \frac{4 t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}} d t$
(c) $\int _{0}^{\sqrt{2}+1} \frac{4 t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}} d t$
(d) $\int _{0}^{\sqrt{2}+1} \frac{t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}} d t$
Show Answer
Answer:
Correct Answer: 32.(b)
Solution:
Formula:
- Required area $=\int _{0}^{\pi / 4} (\sqrt{\frac{1+\sin x}{\cos x}}-\sqrt{\frac{1-\sin x}{\cos x}}) d x$
$ \begin{aligned} & [\because \frac{1+\sin x}{\cos x}>\frac{1-\sin x}{\cos x}>0] \end{aligned} $
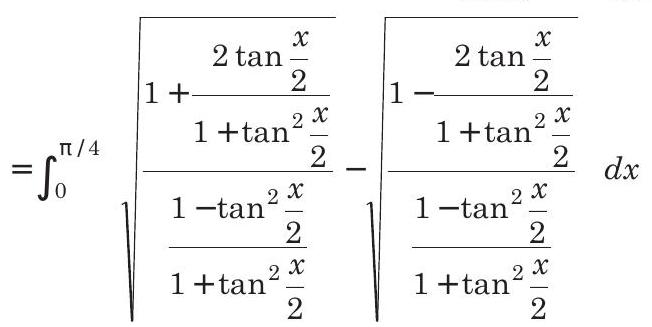
$ \begin{aligned} & =\int _{0}^{\pi / 4} (\sqrt{\frac{1+\tan \frac{x}{2}}{1-\tan \frac{x}{2}}}-\sqrt{\frac{1-\tan \frac{x}{2}}{1+\tan \frac{x}{2}}}) d x \\ & =\int _{0}^{\pi / 4} \frac{1+\tan \frac{x}{2}-1+\tan \frac{x}{2}}{\sqrt{1-\tan ^{2} \frac{x}{2}}} d x=\int _{0}^{\pi / 4} \frac{2 \tan \frac{x}{2}}{\sqrt{1-\tan ^{2} \frac{x}{2}}} d x \end{aligned} $
Put $\tan \frac{x}{2}=t \Rightarrow \frac{1}{2} \sec ^{2} \frac{x}{2} d x=d t=\int _{0}^{\tan \frac{\pi}{8}} \frac{4 t d t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}}$
$ \text { As } \quad \int _{0}^{\sqrt{2}-1} \frac{4 t d t}{\left(1+t^{2}\right) \sqrt{1-t^{2}}} \quad\left[\because \tan \frac{\pi}{8}=\sqrt{2}-1\right] $





