Area Ques 33
Question
- The area bounded by the curves $y=(x-1)^{2}, y=(x+1)^{2}$ and $y=\frac{1}{4}$ is
(2005, 1M)
(a) $\frac{1}{3}$ sq unit
(b) $\frac{2}{3}$ sq unit
(c) $\frac{1}{4}$ sq unit
(d) $\frac{1}{5}$ sq unit
Show Answer
Answer:
Correct Answer: 33.(a)
Solution:
Formula:
- The curves $y=(x-1)^{2}, y=(x+1)^{2}$ and $y=1 / 4$ are shown as
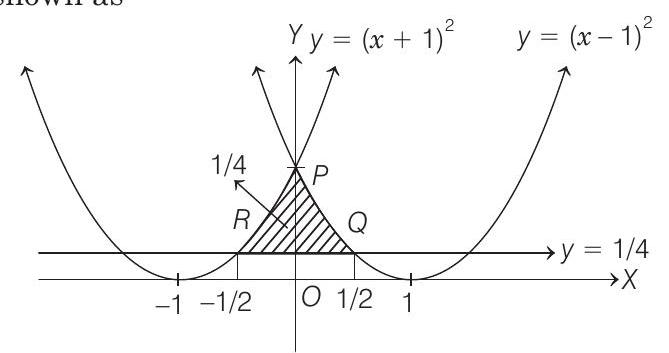
where, points of intersection are
$ (x-1)^{2}=\frac{1}{4} \quad \Rightarrow \quad x=\frac{1}{2} \text { and }(x+1)^{2}=\frac{1}{4} \Rightarrow x=-\frac{1}{2} $
i.e.
$ Q(\frac{1}{2}, \frac{1}{4}) \quad \text { and } \quad R \quad-(\frac{1}{2}, \frac{1}{4}) $
$\therefore \quad$ Required area $=2 \int _{0}^{1 / 2}[(x-1)^{2}-\frac{1}{4}] d x$
$ \begin{aligned} & =2 [\frac{(x-1)^{3}}{3}-\frac{1}{4} x] _{0}^{1 / 2} \\ & =2[-\frac{1}{8 \cdot 3}-\frac{1}{8}-(-\frac{1}{3}-0)] \quad=\frac{8}{24}=\frac{1}{3} \text { sq unit } \end{aligned} $





