Area Ques 34
Question
- The area enclosed between the curves $y=a x^{2}$ and $x=a y^{2}(a>0)$ is 1 sq unit. Then, the value of $a$ is
(a) $\frac{1}{\sqrt{3}}$
(b) $\frac{1}{2}$
(c) $1$
(d) $\frac{1}{3}$
(2004, 1M)
Show Answer
Answer:
Correct Answer: 34.(a)
Solution:
Formula:
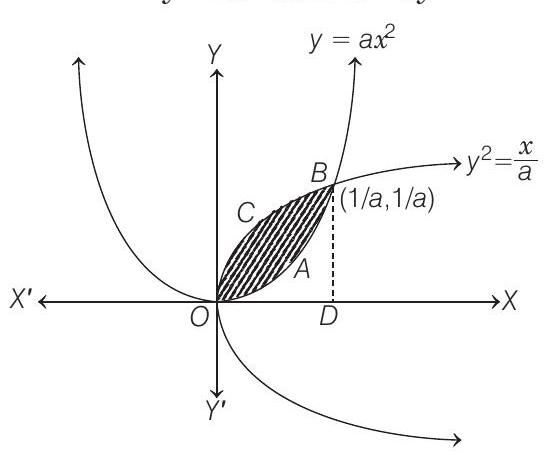
- As from the figure, area enclosed between the curves is $O A B C O$.
Thus, the point of intersection of
$ y=a x^{2} \text { and } x=a y^{2} $
$ \begin{array}{ll} \Rightarrow & x=a\left(a x^{2}\right)^{2} \\ \Rightarrow & x=0, \frac{1}{a} \Rightarrow y=0, \frac{1}{a} \end{array} $
So, the points of intersection are $(0,0)$ and $(\frac{1}{a}, \frac{1}{a})$.
$\therefore$ Required area $O A B C O=$ Area of curve $O C B D O-$ Area of curve $O A B D O$
$\Rightarrow \int _{0}^{1 / a} (\sqrt{\frac{x}{a}}-a x^{2} )d x =1 $
$\Rightarrow [\frac{1}{\sqrt{a}} \cdot \frac{x^{3 / 2}}{3 / 2}-\frac{a x^{3}}{3}]{ }^{1 / a} =1 $
$\Rightarrow \frac{2}{3 a^{2}}-\frac{1}{3 a^{2}} =1 $
$\Rightarrow a^{2} =\frac{1}{3} \Rightarrow \quad a=\frac{1}{\sqrt{3}} $
$\quad[\because a>0]$





