Area Ques 36
Question
- The slope of tanget to a curve $y=f(x)$ at $[x, f(x)]$ is $2 x+1$. If the curve passes through the point $(1,2)$, then the area bounded by the curve, the X-axis and the line $x=1$ is
(a) $\frac{3}{2}$
(b) $\frac{4}{3}$
(c) $\frac{5}{6}$
(d) $\frac{1}{12}$
Show Answer
Answer:
Correct Answer: 36.(c)
Solution:
Formula:
- Given, $\frac{d y}{d x}=2 x+1$
On integrating both sides
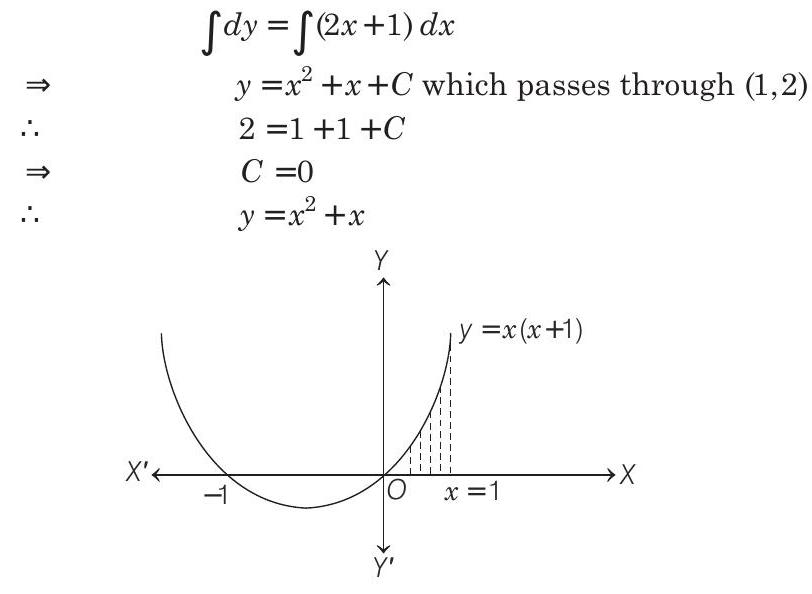
Thus, the required area bounded by $X$-axis, the curve and $x=1$
$ \begin{aligned} & =\int _{0}^{1}\left(x^{2}+x\right) d x=[\frac{x^{3}}{3}+\frac{x^{2}}{2}] _{0}^{1} \\ & =\frac{1}{3}+\frac{1}{2}=\frac{5}{6} \text { sq unit } \end{aligned} $





