Area Ques 38
Question
- If $S$ be the area of the region enclosed by $y=e^{-x^{2}}, y=0, x=0$ and $x=1$. Then,
(2012)
(a) $S \geq \frac{1}{e}$
(b) $S \geq 1-\frac{1}{e}$
(c) $S \leq \frac{1}{4} (1+\frac{1}{\sqrt{e}})$
(d) $S \leq \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{e}} (1-\frac{1}{\sqrt{2}})$
Show Answer
Answer:
Correct Answer: 38.(b,d)
Solution:
Formula:
- PLAN: (i) Area of region $f(x)$ bounded between $x=a$ to $x=b$ is
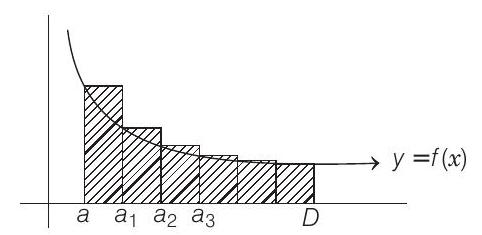
$\int _{a}^{b} f(x) d x=$ Sum of areas of rectangle shown in shaded part.
(ii) If $f(x) \geq g(x)$ when defined in $[a, b]$, then
$ \int _{a}^{b} f(x) d x \geq \int _{a}^{b} g(x) d x $
Description of Situation: As the given curve $y=e^{-x^{2}}$ cannot be integrated, thus we have to bound this function by using above mentioned concept.
Graph for $y=e^{-x^{2}}$
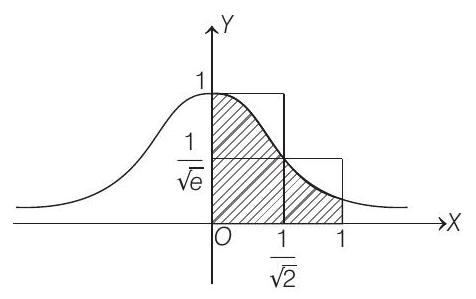
Since, $x^{2} \leq x$ when $x \in[0,1]$
$ \Rightarrow -x^{2} \geq-x \text { or } e^{-x^{2}} \geq e^{-x} $
$ \therefore \int _{0}^{1} e^{-x^{2}} d x \geq \int _{0}^{1} e^{-x} d x $
$\Rightarrow S \geq-\left(e^{-x}\right) _{0}^{1}=1-\frac{1}{e}$ $\quad$ …….(i)
Also, $\int _{0}^{1} e^{-x^{2}} d x \leq$ Area of two rectangles
$\leq (1 \times \frac{1}{\sqrt{2}})+(1-\frac{1}{\sqrt{2}} )\times \frac{1}{\sqrt{e}} $
$\leq \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{e}} (1-\frac{1}{\sqrt{2}})$ $\quad$ …….(ii)
$\therefore \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{e}} (1-\frac{1}{\sqrt{2}}) \geq S \geq 1-\frac{1}{e} \quad$ [from Eqs. (i) and (ii)]





