Area Ques 39
Question
- The area (in sq units) of the region bounded by the curves $y=2^{x}$ and $y=|x+1|$, in the first quadrant is
(a) $\frac{3}{2}$
(b) $\log _{e} 2+\frac{3}{2}$
(c) $\frac{1}{2}$
(d) $\frac{3}{2}-\frac{1}{\log _{e} 2}$
(2019 Main, 10 April II)
Show Answer
Answer:
Correct Answer: 39.(d)
Solution:
Formula:
- Given, equations of curves
$y=2^{x}$ and $y=|x+1|=\begin{array}{cc}x+1 & , x \geq-1 \\ -x-1 & , x<-1\end{array}$
$\because$ The figure of above given curves is
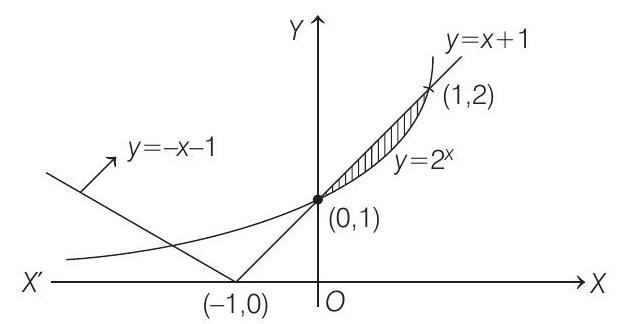
In first quadrant, the above given curves intersect each other at $(1,2)$.
So, the required area $=\int _{0}^{1}\left((x+1)-2^{x}\right) d x$
$ \begin{aligned} & =[\frac{x^{2}}{2}+x-\frac{2^{x}}{\log _{e} 2}]{ } _{0}^{1} \quad [\because \int a^{x} d x=\frac{a^{x}}{\log _{e} a}+C] \\ & =[\frac{1}{2}+1-\frac{2}{\log _{e} 2}+\frac{1}{\log _{e} 2} ]\\ & =\frac{3}{2}-\frac{1}{\log _{e} 2} \end{aligned} $





