Area Ques 41
Question
- For which of the following values of $m$, is the area of the region bounded by the curve $y=x-x^{2}$ and the line $y=m x$ equals $\frac{9}{2}$ ?
$(1999,3 \mathrm{M})$
(a) $-4$
(b) $-2$
(c) $ 2$
(d) $ 4$
Show Answer
Answer:
Correct Answer: 41.(b,d)
Solution:
Formula:
- Case I When $m=0$
In this case, $\quad y=x-x^{2}$ $\quad$ …….(i)
and $ \quad y=0$ $\quad$ …….(ii)
are two given curves, $y>0$ is total region above $X$-axis.
Therefore, area between $y=x-x^{2}$ and $y=0$
is area between $y=x-x^{2}$ and above the $X$-axis
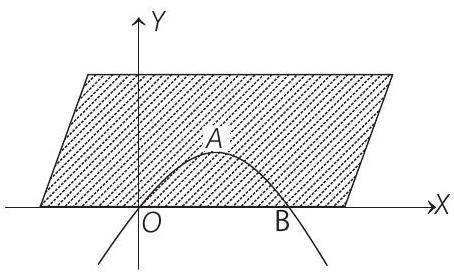
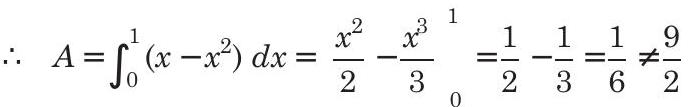
Hence, no solution exists.
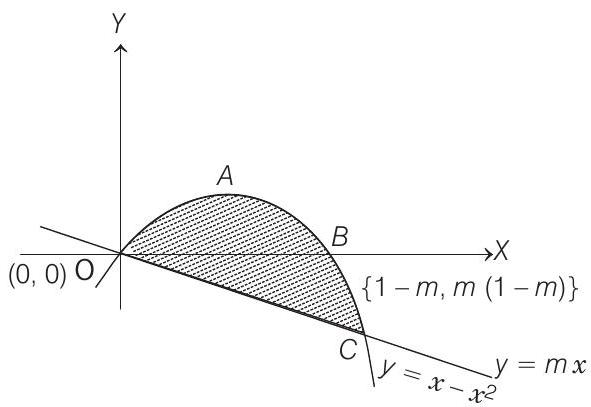
Case II When $m<0$
In this case, area between $y=x-x^{2}$ and $y=m x$ is $O A B C O$ and points of intersection are $(0,0)$ and $\{1-m, m(1-m)\}$.
$\therefore \quad$ Area of curve $O A B C O=\int _{0}^{1-m}\left[x-x^{2}-m x\right] d x$
$ =[(1-m) \frac{x^{2}}{2}-{\frac{x^{3}}{3}}]^{1-m} $
$ =\frac{1}{2}(1-m)^{3}-\frac{1}{3}(1-m)^{3}=\frac{1}{6}(1-m)^{3} $
$\therefore \quad \frac{1}{6}(1-m)^{3} =\frac{9}{2} $
$\Rightarrow \quad(1-m)^{3} =27 $
$\Rightarrow \quad 1-m =3 $
$\Rightarrow \quad m =-2$
Case III When $m>0$
In this case, $y=m x$ and $y=x-x^{2}$ intersect in $(0,0)$ and $\{(1-m), m(1-m)\}$ as shown in figure
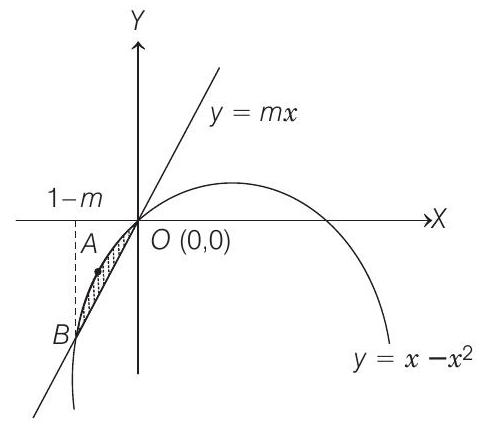
$\therefore$ Area of shaded region $=\int _{1-m}^{0}\left(x-x^{2}-m x\right) d x$
$=[(1-m) \frac{x^{2}}{2}-{\frac{x^{3}}{3}}]^{0} $
$=-\frac{1}{2}(1-m)(1-m)^{2}+\frac{1}{3}(1-m)^{3} $
$=-\frac{1}{6}(1-m)^{3} $
$\Rightarrow \quad \frac{9}{2} =-\frac{1}{6}(1-m)^{3} $
$\Rightarrow \quad(1-m)^{3} =-27 $
$\Rightarrow \quad(1-m) =-3 $
$\Rightarrow \quad m =3+1=4$
[given]
Therefore, (b) and (d) are the answers.





