Area Ques 42
Question
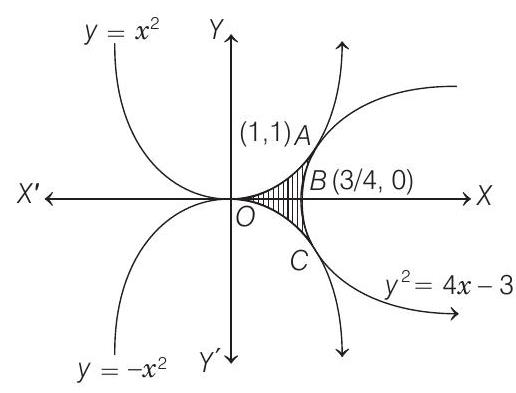
- Find the area bounded by the curves $x^{2}=y, x^{2}=-y$ and $y^{2}=4 x-3$.
$(2005,4\ M)$
Show Answer
Answer:
Correct Answer: 42.($\frac{1}{3} $ sq unit)
Solution:
Formula:
The region bounded by the curves $y=x^{2}, y=-x^{2}$ and $y^{2}=4 x-3$ is symmetrical about the $x$-axis, where $y^{2}=4 x-3$ meets $y=x^{2}$ at $(1,1)$.
$\therefore$ Area of curve $(O A B C O)$
$ =2 \quad [\int _{0}^{1} x^{2} d x-\int _{3 / 4}^{1}(\sqrt{4 x-3}) d x] $
$ \begin{alignedat} & =2[{(\frac{x^{3}}{3})} _{0}^{1}-{(\frac{(4 x-3)^{3 / 2}}{3 \cdot 4 / 2})} _{3 / 4}^{1}] \\ & =2 (\frac{1}{3}-\frac{1}{6}) \\ & =1 \cdot \frac{1}{6}=\frac{1}{3} \mathrm{sq} \text { unit } \end{aligned} $





