Area Ques 45
Question
- Let $b \neq 0$ and for $j=0,1,2 \ldots, n$. If $S _{j}$ is the area of the region bounded by the $Y$-axis and the curve $x e^{a y}=\sin b y, \frac{j \pi}{b} \leq y \leq \frac{(j+1) \pi}{(b)}$. Then, show that
$S _{0}, S _{1}, S _{2}, \ldots, S _{n}$ are in geometric progression. Also, find their sum for $a=-1$ and $b=\pi$.
$(2001,5$ M)
Show Answer
Answer:
Correct Answer: 45.$[\frac{\pi(1+e)}{\left(1+\pi^{2}\right)} \cdot \frac{\left(e^{n+1}-1\right)}{e-1}]$
Solution:
Formula:
- Given, $x=(\sin b y) e^{-a y}$
Now,
$-1 \leq \sin$ by $\leq 1$
$\Rightarrow \quad-e^{-a y} \leq e^{-a y} \sin b y \leq e^{-a y}$
$\Rightarrow \quad-e^{-a y} \leq x \leq e^{-a y}$
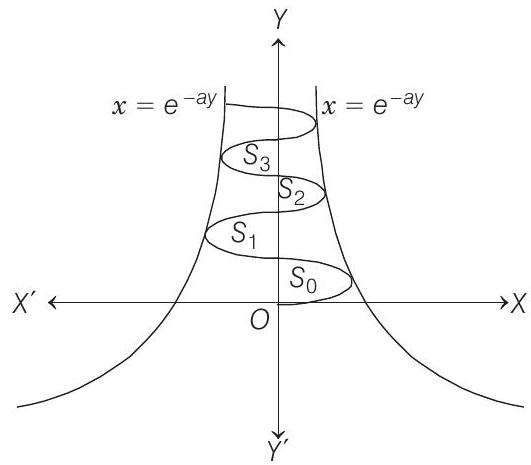
In this case, if we take $a$ and $b$ positive, the values $-e^{-a y}$ and $e^{-a y}$ become left bond and right bond of the curve and due to oscillating nature of sin $b y$, it will oscillate between $x=e^{-a y}$ and $x=-e^{-a y}$
Now, $\quad S _{j}=\int _{j \pi / b}^{(j+1) \pi / b} \sin b y \cdot e^{-a y} d y$
$ [\text { since, } I=\int \sin b y \cdot e^{-a y} d y ]$
$[ I=\frac{-e^{-a y}}{a^{2}+b^{2}} \quad(a \sin b y+b \cos b y) ]$
$ \therefore \quad |S _{j}=\frac{-1}{a^{2}+b^{2}} [e^{\frac{-a(j+1) \pi}{b}} $ $ \{a \sin (j+1) \pi+b \cos (j+1) \pi\} $ $ -e^{\frac{-a j \pi}{b}}(a \sin j \pi+b \cos j \pi) ]|$
$ S _{j}=\mid-\frac{1}{a^{2}+b^{2}}\left[e^{-\frac{a}{b}(j+1) \pi}\left\{0+b(-1)^{j+1}\right\}\right. $ $ \left.-e^{-a j \pi / b}\left\{0+b(-1)^{j}\right\}\right] $
$ =|\frac{b(-1)^{j} e^{-\frac{a}{b} j \pi}}{a^{2}+b^{2}} (e^{-\frac{a}{b} \pi}+1 )|$
$ =e^{-\frac{a}{b} \pi}=\text { constant }$
For $a=-1$ and $b=\pi$
$ \begin{aligned} S _{j} & =\frac{\pi \cdot e^{\frac{1}{\pi} \cdot \pi _{j}}}{\left(1+\pi^{2)}\right.} (e^{\frac{1}{\pi} \cdot \pi}+1)=\frac{\pi \cdot e^{j}}{\left(1+\pi^{2)}\right.}(1+e) \\ \Rightarrow \quad \sum _{j=0}^{n} S _{j} & =\frac{\pi \cdot(1+e)}{(1+\pi)^{2}} \sum _{j=0}^{n} e^{j}=\frac{\pi(1+e)}{\left(1+\pi^{2}\right)}\left(e^{0}+e^{1}+\ldots+e^{n}\right) \\ & =\frac{\pi(1+e)}{\left(1+\pi^{2}\right)} \cdot \frac{\left(e^{n+1}-1\right)}{e-1} \end{aligned} $





