Area Ques 47
Question
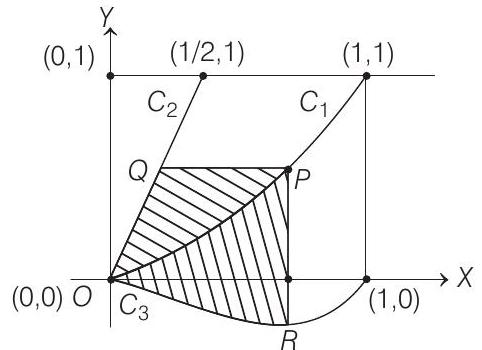
- Let $C _{1}$ and $C _{2}$ be the graphs of functions $y=x^{2}$ and $y=2 x, 0 \leq x \leq 1$, respectively. Let $C _{3}$ be the graph of a function $y=f(x), 0 \leq x \leq 1, f(0)=0$. For a point $P$ on $C _{1}$, let the lines through $P$, parallel to the axes, meet $C _{2}$ and $C _{3}$ at $Q$ and $R$ respectively (see figure). If for every position of $P\left(\right.$ on $\left.C _{1}\right)$ the areas of the shaded regions $O P Q$ and $O R P$ are equal, then determine $f(x)$.
$(1998,8 \mathrm{M})$
Show Answer
Answer:
Correct Answer: 47.$( f(x)=x^{3}-x^{2}, 0 \leq x \leq 1)$
Solution:
Formula:
- Refer to the figure given in the question. Let the coordinates of $P$ be $\left(x, x^{2}\right)$, where $0 \leq x \leq 1$.
For the area $(O P R O)$,
Upper boundary: $y=x^{2}$ and
lower boundary : $y=f(x)$
Lower limit of $x: 0$
Upper limit of $x: x$
$\therefore$ Area $(O P R O)=\int _{0}^{x} t^{2} d t-\int _{0}^{x} f(t) d t$
$ \begin{aligned} & =[{\frac{t^{3}}{3}}] _{0}^{x}-\int _{0}^{x} f(t) d t \\ & =\frac{x^{3}}{3}-\int _{0}^{x} f(t) d t \end{aligned} $
For the area $(O P Q O)$,
The upper curve : $x=\sqrt{y}$
and the lower curve : $x=y / 2$
Lower limit of $y: 0$
and upper limit of $y: x^{2}$
$ \begin{aligned} \therefore \text { Area }(O P Q O) & =\int _{0}^{x^{2}} \sqrt{t} d t-\int _{0}^{x^{2}} \frac{t}{2} d t \\ & =\frac{2}{3}\left[t^{3 / 2}\right] _{0}^{x^{2}}-\frac{1}{4}\left[t^{2}\right] _{0}^{x^{2}} \\ & =\frac{2}{3} x^{3}-\frac{x^{4}}{4} \end{aligned} $
According to the given condition,
$ \frac{x^{3}}{3}-\int _{0}^{x} f(t) d t=\frac{2}{3} x^{3}-\frac{x^{4}}{4} $
On differentiating both sides w.r.t. $x$, we get
$ x^{2}-f(x) \cdot 1=2 x^{2}-x^{3} $
$ \Rightarrow \quad f(x)=x^{3}-x^{2}, 0 \leq x \leq 1 $





