Area Ques 48
Question
- $\operatorname{Let} f(x)=\max \left\{x^{2},(1-x)^{2}, 2 x(1-x)\right\}$, where $0 \leq x \leq 1$.
Determine the area of the region bounded by the curves $y=f(x), X$-axis, $x=0$ and $x=1$.
$(1997,5$ M)
Show Answer
Answer:
Correct Answer: 48.$(\frac{17}{27})$sq unit
Solution:
Formula:
- We can draw the graph of $y=x^{2}, y=\left(1-x^{2}\right)$ and $y=2 x(1-x)$ in following figure
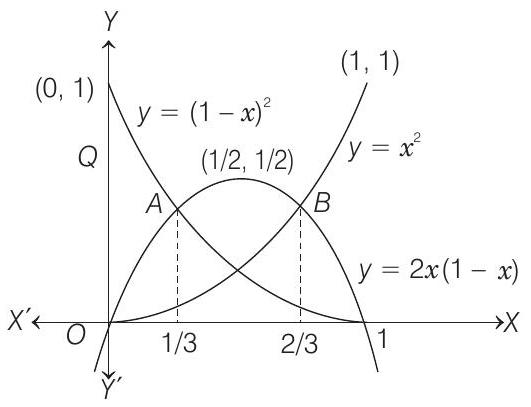
Now, to get the point of intersection of $y=x^{2}$ and $y=2 x(1-x)$, we get
$ x^{2} =2 x(1-x) $
$\Rightarrow 3 x^{2} =2 x $
$\Rightarrow x(3 x-2) =0 $
$\Rightarrow x =0,2 / 3$
Similarly, we can find the coordinate of the points of intersection of
$ y=\left(1-x^{2}\right) \text { and } y=2 x(1-x) \text { are } x=1 / 3 \text { and } x=1 $
From the figure, it is clear that,
$ \begin{array}{cc} (1-x)^{2}, & \text { if } 0 \leq x \leq 1 / 3 \\ f(x)=2 x(1-x), & \text { if } 1 / 3 \leq x \leq 2 / 3 \\ x^{2}, & \text { if } 2 / 3 \leq x \leq 1 \end{array} $
$\therefore$ The required area
$A =\int _{0}^{1} f(x) d x $
$=\int _{0}^{1 / 3}(1-x)^{2} d x+\int _{1 / 3}^{2 / 3} 2 x(1-x) d x+\int _{2 / 3}^{1} x^{2} d x $
$=[-\frac{1}{3}(1-x)]^{1/3}+[x^{2}-{\frac{2 x^{3}}{3}}]^{2 / 3} _{1/3}+[\frac{1}{3} x^{3}]^1 _{2/3}$
$ =[-\frac{1}{3} (\frac{2}{3})^{3}+\frac{1}{3}]+[(\frac{2}{3})^{2}-\frac{2}{3} (\frac{2}{3})^{3}-(\frac{1}{3})^{2}]+[\frac{2}{3} (\frac{1}{3})^{3} ] +[\frac{1}{3}(1)-\frac{1}{3} (\frac{2}{3})^3]$
$ =\frac{19}{81}+\frac{13}{81}+\frac{19}{81}=\frac{17}{27} \text { sq unit } $





