Area Ques 49
Question
- Find all the possible values of $b>0$, so that the area of the bounded region enclosed between the parabolas $y=x-b x^{2}$ and $y=\frac{x^{2}}{b}$ is maximum.
(1997C, 5M)
Show Answer
Answer:
Correct Answer: 49.$(b=1)$
Solution:
Formula:
- Eliminating $y$ from $y=\frac{x^{2}}{b}$ and $y=x-b x^{2}$, we get
$ \begin{aligned} x^{2} & =b x-b^{2} x^{2} \\ \Rightarrow \quad x & =0, \frac{b}{1+b^{2}} \end{aligned} $
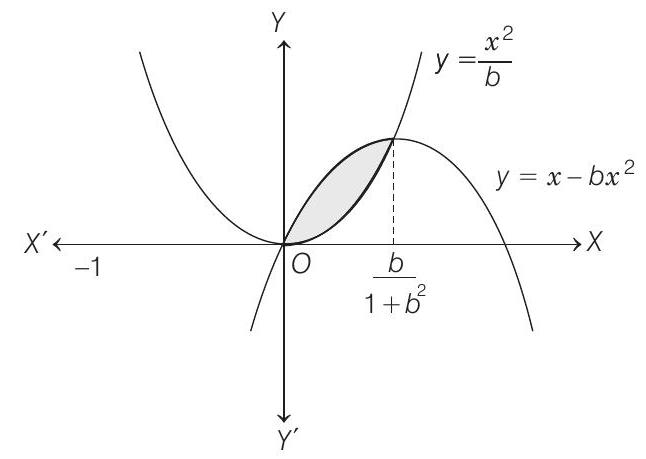
Thus, the area enclosed between the parabolas
$ \begin{aligned} A & =\int _{0}^{b /(1+b)^{2}} (x-b x^{2}-\frac{x^{2}}{b}) d x \\ & =[\frac{x^{2}}{2}-\frac{x^{3}}{3} \cdot{\frac{1+b^{2}}{b}}] _{0}^{b /(1+b)^{2}}=\frac{1}{6} \cdot \frac{b^{2}}{\left(1+b^{2}\right)^{2}} \end{aligned} $
On differentiating w.r.t. $b$, we get
$ \begin{aligned} \frac{d A}{d b} & =\frac{1}{6} \cdot \frac{\left(1+b^{2}\right)^{2} \cdot 2 b-2 b^{2} \cdot\left(1+b^{2}\right) \cdot 2 b}{\left(1+b^{2}\right)^{4}} \\ & =\frac{1}{3} \cdot \frac{b\left(1-b^{2}\right)}{\left(1+b^{2}\right)^{3}} \end{aligned} $
For maximum value of $A$, put $\frac{d A}{d b}=0$
$ \Rightarrow \quad b=-1,0,1 \text {, since } b>0 $
$\therefore$ We consider only $b=1$.
Sign scheme for $\frac{d A}{d b}$ around $b=1$ is as shown below :
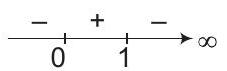
From sign scheme, it is clear that $A$ is maximum at $b=1$.





