Area Ques 50
Question
- The area (in sq units) of the region $A=\{(x, y): \frac{y^{2}}{2} \leq x \leq y+4\}$ is
(2019 Main, 9 April II)
(a) $30$
(b) $\frac{53}{3}$
(c) $16$
(d) $18$
Show Answer
Answer:
Correct Answer: 50.(d)
Solution:
Formula:
- Given region $A=\{(x, y): \frac{y^{2}}{2} \leq x \leq y+4\}$
$ \therefore \quad \frac{y^{2}}{2}=x $
$ \Rightarrow \quad y^{2}=2 x $ $\quad$ …….(i)
and $x=y+4 \Rightarrow y=x-4$ $\quad$ …….(ii)
Graphical representation of $A$ is
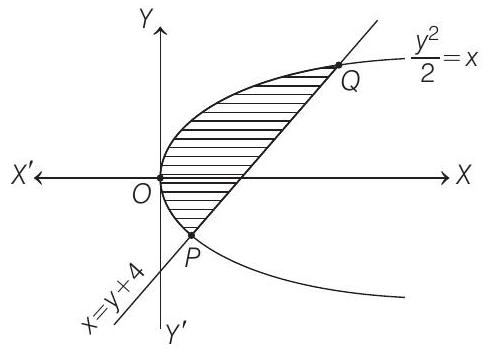
On substituting $y=x-4$ from Eq. (ii) to Eq. (i), we get
$ \begin{array}{rlrl} & & (x-4)^{2} & =2 x \\ \Rightarrow & & x^{2}-8 x+16 & =2 x \\ \Rightarrow & & x^{2}-10 x+16 & =0 \\ \Rightarrow & & (x-2)(x-8) & =0 \\ \Rightarrow & & x & =2,8 \\ \therefore & & y & =-2,4 \end{array} $
[from Eq. (ii)]
So, the point of intersection of Eqs. (i) and
(ii) are $P(2,-2)$ and $Q(8,4)$.
Now, the area enclosed by the region $A$
$ \begin{aligned} & =\int _{-2}^{4}[(y+4)-\frac{y^{2}}{2}] d y=[\frac{y^{2}}{2}+4 y-{\frac{y^{3}}{6}}] _{-2}^{4} \\ & = (\frac{16}{2}+16-\frac{64}{6}) - (\frac{4}{2}-8+\frac{8}{6}) \\ & =8+16-\frac{32}{3}-2+8-\frac{4}{3} \\ & =30-12=18 \text { sq unit. } \end{aligned} $





