Area Ques 51
Question
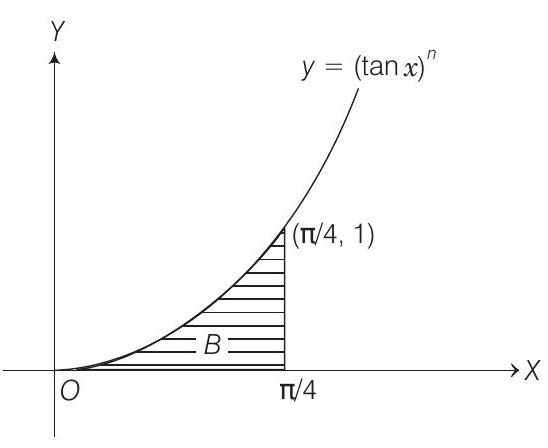
- If $A _{n}$ is the area bounded by the curve $y=(\tan x)^{n}$ and the lines $x=0, y=0$ and $x=\frac{\pi}{4}$.
Then, prove that for $n>2, A _{n}+A _{n+2}=\frac{1}{n+1}$ and deduce $\frac{1}{2 n+2}<A _{n}<\frac{1}{2 n-2}$.
$(1996,3 M)$
Show Answer
Solution:
Formula:
- We have, $A _{n}=\int _{0}^{\pi / 4}(\tan x)^{n} d x$
Since, $0<\tan x<1$, when $0<x<\pi / 4$
We have, $0<(\tan x)^{n+1}<(\tan x)^{n}$ for each $n \in N$
$\Rightarrow \int _{0}^{\pi / 4}(\tan x)^{n+1} d x<\int _{0}^{\pi / 4}(\tan x)^{n} d x$
$\Rightarrow \quad A _{n+1}<A _{n}$
Now, for $n>2$
$ \begin{aligned} A _{n}+A _{n+2} & =\int _{0}^{\pi / 4}\left[(\tan x)^{n}+(\tan x)^{n+2}\right] d x \\ & =\int _{0}^{\pi / 4}(\tan x)^{n}\left(1+\tan ^{2} x\right) d x \end{aligned} $
$=\int _{0}^{\pi / 4}(\tan x)^{n} \sec ^{2} x d x$
$=[\frac{1}{(n+1)}(\tan x)^{n+1}]^{\pi /4} _0$
$=\frac{1}{(n+1)}(1-0)=\frac{1}{n+1}$
Since, $\quad A _{n+2}<A _{n+1}<A _{n}$,
then $\quad A _{n}+A _{n+2}<2 A _{n}$
$\Rightarrow \quad \frac{1}{n+1}<2 A _{n}$
$\Rightarrow \quad \frac{1}{2 n+2}<A _{n}$ $\quad$ …….(i)
Also, for $n>2 A _{n}+A _{n}<A _{n}+A _{n-2}=\frac{1}{n-1}$
$\Rightarrow 2 A _{n}<\frac{1}{n-1} $
$\Rightarrow A _{n}<\frac{1}{2 n-2}$ $\quad$ …….(ii)
From Eqs. (i) and (ii), $\frac{1}{2 n+2}<A _{n}<\frac{1}{2 n-2}$





