Area Ques 52
Question
- Consider a square with vertices at $(1,1),(-1,1),(-1,-1)$ and $(1,-1)$. If $S$ is the region consisting of all points inside the square which are nearer to the origin than to any edge. Then, sketch the region $S$ and find its area.
$(1995,5$ M)
Show Answer
Answer:
Correct Answer: 52.$[\frac{1}{3}(16 \sqrt{2}-20)]$ sq units
Solution:
Formula:
- The equations of the sides of the square are as follow :
$ A B: y=1, B C: x=-1, C D: y=-1, D A: x=1 $
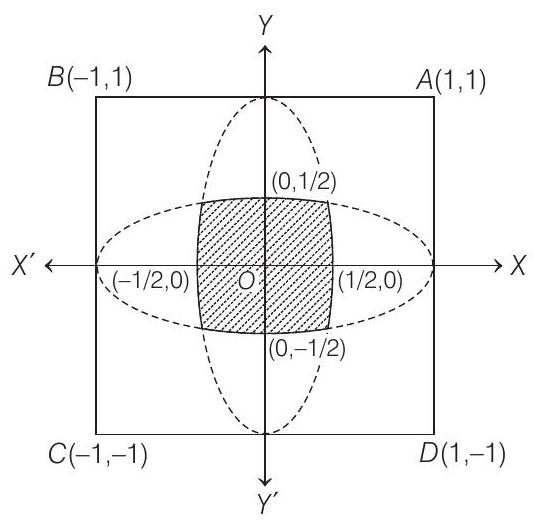
Let the region be $S$ and $(x, y)$ is any point inside it.
Then, according to given conditions,
$ \begin{array}{lc} & \sqrt{x^{2}+y^{2}}<|1-x|,|1+x|,|1-y|,|1+y| \\ \Rightarrow & x^{2}+y^{2}<(1-x)^{2},(1+x)^{2},(1-y)^{2},(1+y)^{2} \\ \Rightarrow & x^{2}+y^{2}<x^{2}-2 x+1, x^{2}+2 x+1, \\ & y^{2}-2 y+1, y^{2}+2 y+1 \\ \Rightarrow & y^{2}<1-2 x, y^{2}<1+2 x, x^{2}<1-2 y \text { and } x^{2}<2 y+1 \end{array} $
Now, in $y^{2}=1-2 x$ and $y^{2}=1+2 x$, the first equation represents a parabola with vertex at $(1 / 2,0)$ and second equation represents a parabola with vertex $(-1 / 2,0)$ and in $x^{2}=1-2 y$ and $x^{2}=1+2 y$, the first equation represents a parabola with vertex at $(0,1 / 2)$ and second equation represents a parabola with vertex at $(0,-1 / 2)$.
Therefore, the region $S$ is lying inside the four parabolas
$ y^{2}=1-2 x, y^{2}=1+2 x, x^{2}=1+2 y, x^{2}=1-2 y $
where, $S$ is the shaded region.
Now, $S$ is symmetrical in all four quadrants, therefore $S=4 \times$ Area lying in the first quadrant.
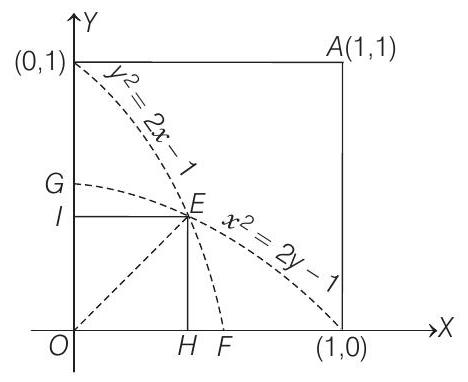
Now, $y^{2}=1-2 x$ and $x^{2}=1-2 y$ intersect on the line $y=x$. The point of intersection is $E(\sqrt{2}-1, \sqrt{2}-1)$.
Area of the region $O E F O$
=Area of $\triangle O E H+$ Area of $H E F H$
$ \begin{aligned} & =\frac{1}{2}(\sqrt{2}-1)^{2}+\int _{\sqrt{2}-1}^{1 / 2} \sqrt{1-2 x} d x \\ & =\frac{1}{2}(\sqrt{2}-1)^{2}+[(1-2 x)^{3 / 2} \frac{2}{3} \cdot \frac{1}{2}(-1)]^{1 / 2} \\ & =\frac{1}{2}(2+1-2 \sqrt{2})+\frac{1}{3}(1+2-2 \sqrt{2})^{3 / 2} \end{aligned} $
$ \begin{aligned} & =\frac{1}{2}(3-2 \sqrt{2})+\frac{1}{3}(3-2 \sqrt{2})^{3 / 2} \\ & =\frac{1}{2}(3-2 \sqrt{2})+\frac{1}{3}\left[(\sqrt{2}-1)^{2}\right]^{3 / 2} \\ & =\frac{1}{2}(3-2 \sqrt{2})+\frac{1}{3}(\sqrt{2}-1)^{3} \\ & =\frac{1}{2}(3-\sqrt{2})+\frac{1}{3}[2 \sqrt{2}-1-3 \sqrt{2}(\sqrt{2}-1)] \\ & =\frac{1}{2}(3-2 \sqrt{2})+\frac{1}{3}[5 \sqrt{2}-7] \\ & =\frac{1}{6}[9-6 \sqrt{2}+10 \sqrt{2}-14]=\frac{1}{6}[4 \sqrt{2}-5] \text { sq units } \end{aligned} $
Similarly, area $O E G O=\frac{1}{6}(4 \sqrt{2}-5)$ sq units
Therefore, area of $S$ lying in first quadrant
$ =\frac{2}{6}(4 \sqrt{2}-5)=\frac{1}{3}(4 \sqrt{2}-5) \text { sq units } $
Hence, $S=\frac{4}{3}(4 \sqrt{2}-5)=\frac{1}{3}(16 \sqrt{2}-20)$ sq units





